Magnetic characteristics of iron nanoclusters

It is known that the nanocrystalline state changes not only the structure, but also many physical characteristics of substances [1]. The paper [2] presents studies of the magnetic properties of iron cluster particles with different numbers of atoms. It is shown that the ferromagnetic properties of iron clusters depend on the number of atoms in them. For clusters smaller than 50 atoms, the magnetic moments reach 3.1 Bohr magnetons. As the number of atoms increases to 500–700 in the cluster, the magnetic moments approach the magnetization of bulk samples, which is 2.2 Bohr magnetons (Fig. 1).

The authors [3] found the presence of magnetization in cluster formations even in the absence of ferromagnetic atoms in them. Hysteresis loops confirming magnetization were obtained for CeO 2 , GaN, Al 2 O 3 , and other clusters. Ferromagnetism is also observed in thin films of HfO 2 , TiO 2 , ZnO [4; 5].

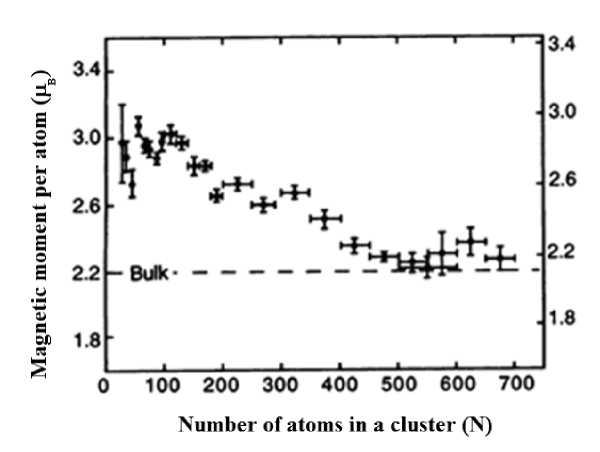
Рис. 1. Зависимость среднего магнитного момента на атом для кластеров железа от числа атомов в нём при 120 К [2]

Fig. 1. Dependence of the average magnetic moment per atom for iron clusters on the number of atoms in it at 120 K [2]

Cluster models are the most objective representation of the structure of metals with a small number of atoms [6]. In addition, structures corresponding to cluster structures also occur in the volume of metals, at interfaces, fracture surfaces, etc. When modeling nanocluster formations, we use sets of close-packed tetrahedron assemblies that most adequately correspond to the nanocrystalline state [7].

Purpose of work

The purpose of work is to explain the nature of the magnetization increase of iron in nanocluster formations containing different numbers of atoms.

Objectives of the work

• 1.    Construction of three-dimensional cluster models of tetrahedral close-packed iron nanoclusters with different numbers of atoms.

• 2.    Construction of electron density spectra of the investigated nanoclusters.

Methods

To determine the coordinates of the atoms, spatial models of the clusters were constructed using a threedimensional modeling program. The program has the necessary tools to determine the coordinates of atoms of the studied clusters. The cluster models were based on theoretical values of iron crystal lattice parameters: a ГЦК = 3.656 Å, а ОЦК = 2.866 Å [8].

The density spectra of electron states were constructed within the framework of the density functional theory (DFT) [9] using the basis of plane waves and ultrasoft pseudopotentials. The calculation was carried out by the scattered wave method (SW) in accordance with the zone theory of crystals, an analogue of the Korringa – Kohn – Rostoker method, adapted for cluster models. The SW method is based on the formalism of multiple scattering of electron waves on a system of potentials. It allows us to perform calculations based on atomic nuclei coordinates for clusters of several atoms and large systems. The interaction of electrons is described by averaged values of periodic fields described by the MT-potential [10]. The QuantumEspresso software package [11] was used for the calculations.

Results

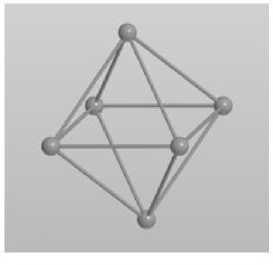
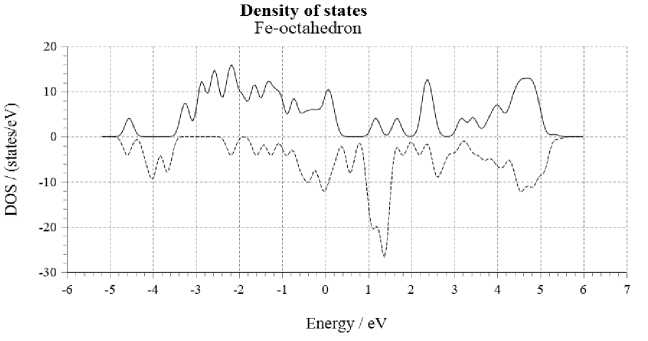
At the first stage, a model of octahedral cluster for iron of face-centered crystal lattice modification including six atoms was constructed (Fig. 2, a ). Further, the probability density diagram of electron states for the above cluster was obtained (Fig. 2, б ).

а

б

Рис. 2. Октаэдрический кластер ГЦК-железа из шести атомов:

а – общий вид; б – зависимость плотности вероятности распределения электронных состояний от энергии электронов со спином вверх и вниз

• Fig. 2.    Octahedral cluster of fcc iron of six atoms:

a – general view; b – dependence of the probability density of the distribution of electronic states on the energy of electrons with spin up and down

According to the spectrum data (Fig. 2, б ), we can conclude that the electron moments with opposite spins are uncompensated. The calculated average effective magnetic moment per atom was 1.67 μ B /atom. This result contradicts the data obtained for the magnetization of austenitic steels having a FCC lattice, which do not exhibit ferromagnetic properties for massive samples [8].

An octahedral cluster of six atoms can be transformed into a cluster formation consisting of close-packed tetrahedrons. According to [12], an octahedron can be transformed into three bound tetrahedrons by switching one chemical bond between two atoms out of six (Fig. 3).

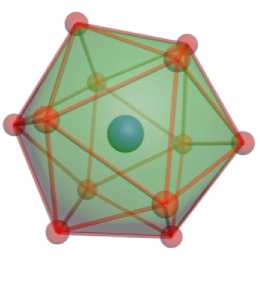
Tetrahedral assemblies can be organized in different ways. The best known example is the Franck – Kasper structure FK-12 [13], which corresponds to an icosahedron. Such an assembly can be constructed from twenty close-packed tetrahedrons (Fig. 4, a ).

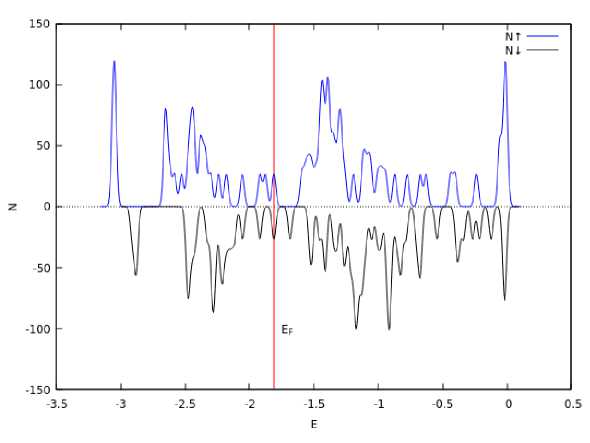
Calculation of the density of electronic states of the icosahedral cluster (Fig. 4, б ) showed that the average magnetic moment is 0.21 μ B /atom.

It is known that the structure FK-12 along with FK-14 appears in Hadfield steel 110Г13Л during plastic deformation on the deformation or fracture surface. Hadfield steel is also austenitic, but exhibits non-zero magnetization under mechanical action [14].

Рис. 3. Преобразование нанокластеров:

а – модель откаэдрического кластера; б – модель кластера из трёх тетраэдров [12]

• Fig. 3.    Transformation of nanoclusters:

a – model of a hexagonal cluster; b – model of a cluster of three tetrahedra [12]

а

б

Рис. 4. Икосаэдрический кластер железа из 13 атомов:

а – общий вид; б – зависимость плотности вероятности распределения электронных состояний от энергии электронов со спином вверх и вниз; вертикальная линия соответствует энергии Ферми

• Fig. 4.    Icosahedral iron cluster of 13 atoms:

a – general view; b – dependence of the probability density of the distribution of electronic states on the energy of electrons with spin up and down; the vertical line corresponds to the Fermi energy

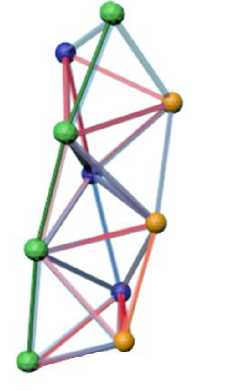
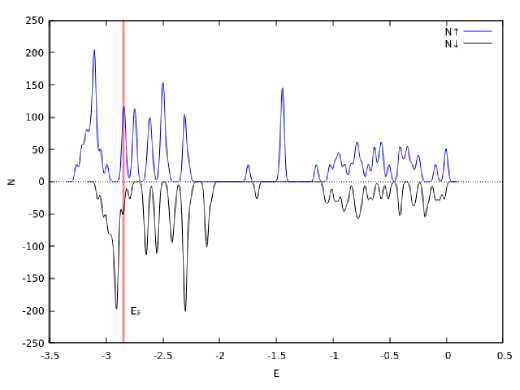
There are various possibilities of packing tetrahedrons in a nanocluster. Thus, the formation of a cluster in the form of a tetrahedral helix for compounds Ni 4 Ti 3 , Al 4 C 3 , etc. was shown in [12; 15; 16]. The formation of such a structure is related to the possibility of transition of an octahedral cluster into a group of three tetrahedral ones (see Fig. 3). Fig. 5, a shows a nanocrystalline iron cluster representing a helix of seven tetrahedrons. A spin-polarized density of electron states was plotted for such a tetrahedral assembly (Fig. 5, б ); the average magnetic moment per atom was 0.26 μ B /atom.

When further coordination spheres are constructed (Fig. 6) using tetrahedral clusters, the number of atoms on the surface increases with geometric progression. The central atom in the center is common to all spirals. The first row of tetrahedrons is located on top and has 12 generalized atoms between them on the surface. The second row has 20 atoms on the surface, the third has 32 atoms, the fourth has 52 atoms, etc. (Fig. 6).

However, according to Delaunay's rule [6], it is impossible to realize in three-dimensional space a close-packed structure of an icosahedron containing more than 2 coordination spheres.

а

б

Рис. 5. Спиральный кластер железа, составленный из семи тетраэдров: а – общий вид; б – зависимость плотности вероятности распределения электронных состояний от энергии электронов со спином вверх и вниз

• Fig. 5.    Spiral iron cluster, composed of seven tetrahedra: a – general view; b – dependence of the probability density of the distribution of electronic states on the energy of electrons with spin up and down

  

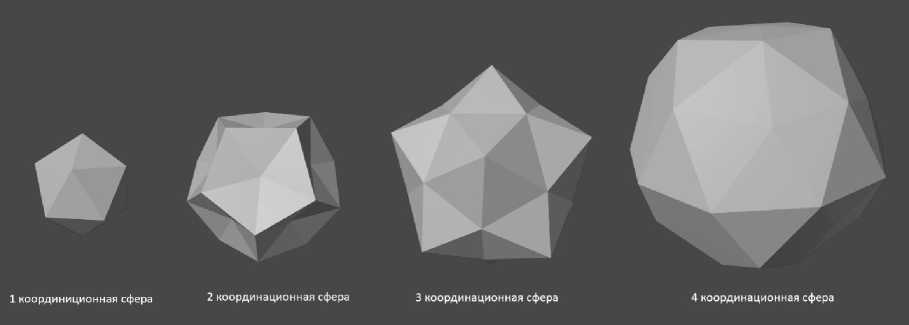
  Рис. 6. Эволюция координационных сфер из тетраэдрических кластеров: от первой до четвёртой

  Fig. 6. Evolution of coordination spheres from tetrahedral clusters: from the first to the fourth

  
  

The next stage of modeling was the combination of a spiral and icosahedral cluster. When twenty tetrahedral spirals are close-packed (Fig. 7), an icosahedron containing 13 atoms is formed in the first coordination sphere. The second coordination sphere contains 20 atoms. Here the first 3 tetrahedrons from each of the 20 spirals are connected in a coordinated manner. Then each spiral grows independently in the direction from the center perpendicular to the faces of the first coordination sphere. Each helix has 10 atoms, 6 of which, packed in 3 tetrahedrons, are in 2 coordination spheres. The remaining 4 atoms of each helix are packed into "tails" of 4 tetrahedrons. The total number of atoms in such positions is 4 × 20 = 80. Thus, the total number of atoms in the cluster packed with 20 tetrahedral spirals is 33 + 80 = 113 atoms (Fig. 6).

а

Рис. 7. Комбинация икосаэдрического и спиралевидного кластеров железа: а – неполная модель из бумаги; б – трехмерная компьютерная модель

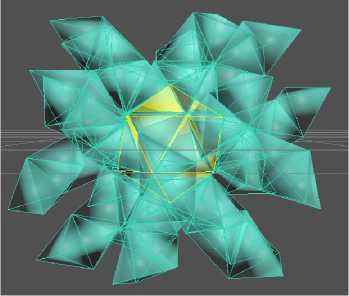
б

Fig. 7. Combination of icosahedral and spiral iron clusters: a – incomplete paper model; b – three-dimensional computer model

Fig. 7 shows a structure built of 20 tetrahedral ten-atom spirals with one common atom in the center. The second coordination sphere also forms an icosahedron containing 20 atoms. Here we get 33 atoms in total in the first and second coordination spheres. This structure corresponds to the experimentally obtained result with the maximum magnetization shown in Fig. 1.

Conclusion

The appearance of magnetization in cluster formations is associated with excited electronic states of those atoms that are on the surface of a nanoparticle or nanofilm. Stressed nonequilibrium electronic states appear in such systems. For small-sized cluster models, most of the atoms are on the surface and have open bonds. The excited atoms have increased electron density, i.e., the electrons are able to move into states with higher energy, approaching the Fermi energy. In this case, the Stoner criterion necessary for the emergence of magnetization is fulfilled [17]. The configurations of electrons with spin up and down are different, resulting in uncompensated magnetic moments. Thus, the proposed models of iron nanoclusters correspond quite satisfactorily to the experimental data of [1].