Магнитное поле газопровода как модель горизонтального кругового цилиндра

Любое намагниченное тело можно представить в виде сочетания положительной +m и отрицательной – m “магнитных масс” в соответствии с рис. 1. Форма и интенсивность магнитных аномалий зависят в первую очередь от расстояния между полярными магнитными массами и их положения относительно поверхности Земли.

Рис. 1. Схема расчета потенциала магнитного диполя.

Потенциал магнитного диполя в некоторой точке земной поверхности определяется из выражения:

M

U = —rcos в , (1) R²

Для одиночного диполя, заключенного в элементарном объеме dW, выражение dU (1) с учетом того, что M = J^dW , можно представить как:

J *cos в dU =---5--- dW , (2)

r

Но поскольку намагниченное тело состоит из множества элементарных объемов, создающих некоторое поле U , то, чтобы найти потенциал реального тела объемом W , необходимо проинтегрировать величину dW по всему объему W

® J *cos в —d- ^dW , (3) W ^r

Полученное выражение лежит в основе решения всех задач магниторазведки. Подставляя в формулу (1) конкретные значения W для тел различной формы, и затем, беря производную от потенциала по вертикальной и горизонтальной составляющей, можно получить выражение для магнитного потенциала U данного тела и его компонент A Z , A H .

Для удобства восприятий о том, как выглядит магнитное поле газопровода, сваренного из отдельных одиннадцатиметровых труб в единую нитку, надо предположить, что длина магнитного диполя газопровода равна длине самой нитки. И этот магнитный диполь - един, и не состоит из суммы диполей каждой одиннадцатиметровой трубы. Тогда газопровод можно представить как цилиндр бесконечной длины. А магнитное поле кругового цилиндра бесконечной длины, лежащего горизонтально, равно полю двух нитей полюсов, расположенных на бесконечно близком расстоянии одна от другой вдоль центральной линии цилиндра.

Следуя рассуждениям А.А. Логачева и В.П. Захарова [1], получим для вертикальной Z и горизонтальной Н составляющих вектора напряженности магнитного поля в сечении, перпендикулярном цилиндру. Поле цилиндра эквивалентно полю бесконечного числа горизонтальных магнитных диполей, центры которых расположены на оси цилиндра. Тогда магнитный потенциал U в точке P земной поверхности (ось Х) от элемента цилиндра будет равен:

dm *cos в J * h * dS * dy dU =     2    =------3---- (4)

r2

/  2  ,     2  ,  7 2

где r = xx + y + h , cos в = —

r

Для нахождения потенциала U по всей длине бесконечного цилиндра нужно выражение (2) проинтегрировать в бесконечных пределах:

+^

U = J * h dS [ ,      y       ,(5)

^J S   Iv< x ² + y ² + h ²)²

Поскольку двойной интеграл определяет площадь поверхности сечения цилиндра JJ dS = S , тогда вто-

S рой интеграл будет равен:

+^

-TO

dy

V( x ² + y ² + h ² ) ²

x² + h ²

то для потенциала цилиндра имеем

U = T =

2* J * S * H

2,12

x + h

, (7)

Дифференцируя полученное выражение по h и x, найдем вертикальную и горизонтальную составляющие Δ Z и Δ H магнитного поля цилиндра при вертикальной намагниченности

A Z =

d V

6 h

2     2

= 2* J * S h  x^

( h ² + x²)²

A H =

д V

9 x

4* j * S * x ( h ² + x ²)²

, (8)

В вышеприведенных формулах: Z - вертикальная составляющая напряженности магнитного поля; Н -горизонтальная составляющая; Т - полная напряженность магнитного поля; h - расстояние от земной поверхности до оси трубопровода; х - расстояние по горизонтали от оси трубопровода в соответствии с рис. 2.

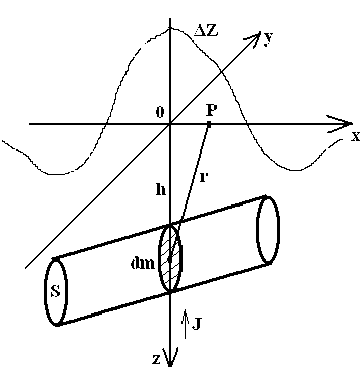
Рис. 2. К расчёту магнитного поля цилиндра.

Непосредственно над трубопроводом Z и Т - максимальны и равны друг другу, а Н - переходит через нуль.

Для косого намагничивания, что чаще всего и имеет место,

(h2 - x2)cos 9 - 2hx sin 9

Z = 2 M                        , (9)

(h2 + x2)2

(h2 - x2) sin 9 - 2hx cos 9

H = - 2 M                      , (10)

(h2 + x2)2

В формулах 7 - 8 M = n R ² J - магнитный момент кругового цилиндра как бы единичной длины, вырезанный из данного бесконечно длинного цилиндра и перпендикулярен его простиранию; где 0 - угол намагничивания; h –расстояние до оси цилиндра. В формулах опущен постоянный множитель и учтен размагничивающий фактор [2, 3],

Для случая вертикального намагничивания 0 = 0 и формулы принимают простой вид (8).

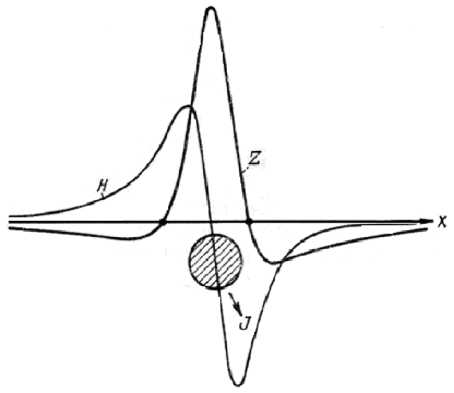
Рис. 3. Кривые Z и Н над горизонтальным круговым цилиндром при косом намагничивании.

Непосредственно над трубопроводом Z и Т, так же как и при вертикальном намагничивании, - максимальны и равны друг другу, а Н - переходит через нуль. Отметим, что при косом намагничивании аномалии несимметричны.

2M

h2  ’

H = 0;

2M

h2 ’

На самом деле при магнитометрии трубопроводов измеряется векторная сумма индуцированного поля трубопровода (или других полей) и магнитное поле Земли. В северных широтах поле Земли направлено под углом к горизонту, поэтому график суммарного поля должен быть несимметричным. Далее, как правило, магнитное поле Земли вычитается из результатов измерений [4].

Реальный трубопровод состоит из сваренных труб длиной каждая около 11 м. Как показано ниже, магнитное поле такого трубопровода нельзя рассматривать как магнитное поле бесконечного цилиндра. Поэтому представляет интерес решение прямой задачи для цилиндра конечной длины. До настоящего времени аналитическое выражение для такого магнитного поля не получено [5]. Однако с некоторым приближением цилиндр конечной длины можно рассматривать как эллипсоид вращения.

Исследуя аналитическое выражение магнитного поля эллипсоидов вращения И.М. Бахурин установил, что магнитное поле со-фокусных эллипсоидов вращения пропорционально их магнитным моментам. Поэтому он предположил, что магнитные поля эллиптических цилиндров можно представлять в виде диаграммы, пользуясь которой можно вычислить напряженность поля (Z и Н) над любым эллиптическим цилиндром. За единицу длины принято q /2 - половина фокусного расстояния q (диаметра), в этих единицах даны координаты точек в вертикальной плоскости, проходящей через центр эллипсоида.

На рисунке 4. изображен разрез эллипсоида вращения с соотношением сторон с:а = 10, намагниченность его предполагается вертикальной, магнитная восприимчивость χ = 1 СГС, намагничивающее поле Т = 0,5 Э, коэффициент размагничивания N = 10,8 ; линии равных значений Z и H даны в миллиэрстедах.

Чтобы вычертить кривую Z (или Н), нужно выбрать уровень, соответствующий глубине залегания центра сечения в единицах q, и по изолиниям снять соответствующие значения. Чтобы найти напряженность поля над эллипсоидом с другим соотношением осей и другой намагниченностью, нужно найти отношение магнитных моментов М 1 : М , где М 1 - момент заданного эллипсоида, а М - изображенного на рисунке. Снятые с рисунка значения нужно умножить на это соотношение.

Магнитные поля цилиндров И. М. Бахурин также представил в виде диаграмм, пользуясь которыми можно вычислить напряженность поля над любым эллиптическим цилиндром.

На рисунках 4 и 5 изображены кривые Z и Н над эллиптическим цилиндром с соотношением осей с:а=10 (соответствует длине трубы 11 м при диаметре 1200 мм) при Т =0,5 Э, χ=1 СГС (что существенно меньше магнитной восприимчивости трубной стали) при вертикальным и косом намагничивании. За единицу длины принята половина фокусного расстояния. Коэффициент размагничивания принят равным 4π /11, где 11 – есть длина трубы газопровода в метрах. Тогда, после математических действий получим, что коэффициент размагничивания будет равен: 4х3,14 /11=1,1418

Вектор J не совпадает с вектором намагничивающего поля – он отклоняется в сторону большей оси сечения. Для вычисления напряженности поля при других условиях кроме соотношения магнитных моментов нужно находить угол расхождения между векторами T и J и снимать значения Z и H в новой системе координат, повернутой относительно первоначальной на угол, равной разности между старым и новым направлениями J при неизменном направлении Т .

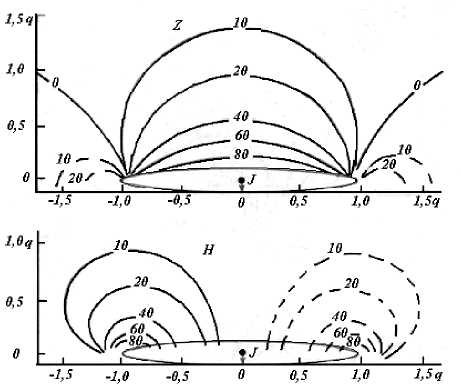
Рис. 4. Магнитное поле Z и Н над эллипсоидом вращения при вертикальном намагничивании.

Особенностью вертикальной составляющей магнитного поля Z при косом намагничивании является резкая ассиметрия магнитного поля. Переход через нулевые значения справа смещен почти на половину фокусного расстояния от края эллипсоида, тогда как слева он проецируется на его край. Поле Н – более симметрично.

Аномалии магнитного поля даже одной трубы имеют сложную форму. А трубопровод – это и сочленение труб с различной намагниченностью, часто разного направления, и аномалии дефектов стали, и аномалии напряженного состояниея металла, и многое другое. Мы не нашли достаточно точного решения задачи для трубопровода, как для полого цилиндра, однако из общих соображений можно предположить, что вектор остаточной намагниченности, полученной при изготовлении трубы на заводе, направлен по обра- зующей трубы, а индуцированной, то есть рабочей – под некоторым углом к ней.

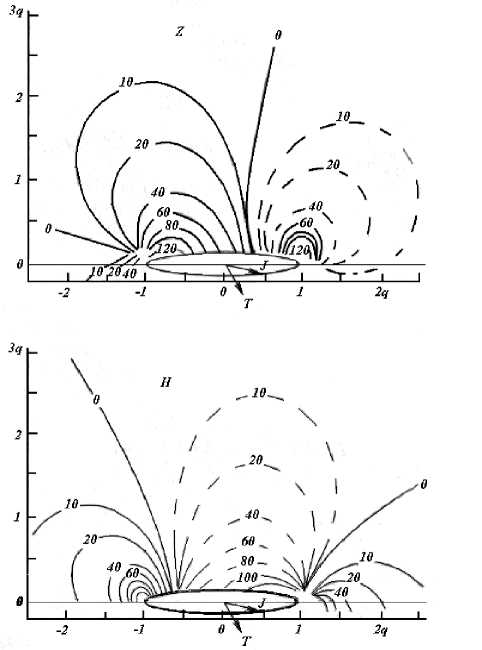
Рис. 5. Магнитное поле Z и Н над горизонтальным эллиптическим цилиндром при косом намагничивании (штрих – положительные значения).

Поэтому, теоретически определить аномалию над совокупностью труб с различным намагничиванием тем более сложно. По нашему мнению для этих целей необходимо использовать математические методы расчета магнитных полей эллипсоидов вращения при вертикальном и косом намагничивании, в виде диаграмм Бахурина И.М., с поправками на фокусное расстояние, например, как для точек по линии пикетов конечно-элементного анализа.