Магнитные превращения в нестехиометрических минералах типа пирротина

Нестехиометрические соединения могут резко изменять свои физические свойства в зависимости от температуры. Так, пирротины – сульфиды железа FeS – Fe7S8, обладающие кристаллической структурой типа NiAs, в которой содержатся катионные вакансии, могут при нагревании переходить из антиферромагнитного состояния в ферромагнитное [1–4]. Для сульфидов железа установлено, что магнитное превращение «антиферромагнетик–ферримагнетик» происходит в результате упорядочения вакансий в четных (нечетных) базисных плоскостях [1; 4; 5]. Действительно, в структуре сульфидов железа в базисных плоскостях реализуется ферромагнитное спиновое упорядочение, а в соседних базисных плоскостях – антиферромагнитное [1; 2], поэтому при равновероятно расположенных вакансиях в четных и нечетных базисных плоскостях суммарный магнитный момент подрешеток скомпенсирован и соединения проявляют свойства антиферромагнетика. Если существует преимущественное расположение вакансий в четных (нечетных) базис- ных плоскостях, то происходит раскомпенсация магнитных подрешеток и соединение становится ферримагнетиком.

До настоящего времени не объяснены причины, в результате которых происходит упорядочение вакансий в четных (нечетных) базисных плоскостях. Поэтому пока не создана теория, описывающая поведение намагниченности несте- хиометрических ферримагнетиков при воздействии высоких температур. Попытаемся дать объяснение физической природы эффекта упорядочения вакансий при нагревании в нестехиометрических соединениях на примере пирротина и предложим теоретическую модель поведения вакансий, объясняющую изменение намагниченности нестехиометрических ферримагнетиков при изменении концентрации вакансий в их структуре.

За элементарную ячейку возьмем простую ячейку структуры типа NiAs (рис. 1). Тот факт, что при определенной температуре вакансии изменяют тип упорядочения в кристаллической структуре, позволяет ввести взаимодействие между вакансиями, смоделировав потенциал этого взаимодействия определенным образом.

Выбор радиуса действия потенциала пояснен на рис. 1, а и б . Потенциал взаимодействия задан таким образом, что он запрещает появление в ячейке более 0,25 вакансий. Если вакансии нет, то ячейка содержит два иона железа и два иона серы.

Для нахождения теоретической зависимости величины намагниченности пирротинов от температуры применим методы квантовой статистики и приближение молекулярного поля. При нагревании нестехиометрических соединений, в отличие от нагревания других минералов, не только изменяется обменное взаимодействие, но и происходит перераспределение катионных вакансий.

ионы S

ионы Fe

α

β

в

б

а

Рис. 1. Проекции элементарной ячейки [2]: а , в – вдоль оси с ; б – вдоль оси а

Отметим, что эти два процесса одновременно еще не рассматривались, хотя именно их взаимное влияние и обусловливает ряд особых свойств нестехиометрических минералов.

Вакансии в кристалле можно представить как некоторую систему из N тождественных частиц. Оператор числа вакансий на узле решетки может иметь собственные значения, равные нулю или единице, что соответствует статистике Ферми– Дирака. Распределение вакансий по разным узлам может быть любым, поэтому статистика вакансий должна быть статистикой Паули. Для описания энергетических состояний вакансий необходимо ввести операторы рождения и уничтожения вакансии на некотором узле p кристаллической решетки, причем a pap = n p,         [а1,’ aq ] = ^pq(1 2np),

{ apaq1^        a p =a + )2 = 0, где p – номер узла кристаллической решетки. Фурье-образ функции Грина [6; 7]

.                +to

(ap\ a g)E = I G pq ( t V Etdt,

-to где G pq (t )= - i ^(t X ap (t )| ag (0 ^ - функция Грина; Q(t) = |0 t>0|, здесь t - переменная времени

Гамильтониан, описывающий вакансионные состояния, можно взять в простейшей форме:

H = I epagap 'I Vpqnpnq, p               p,q где первая сумма описывает независимые вакансии, вторая – их взаимодействие.

Если в некотором узле образовалась вакансия, то энергия магнитного взаимодействия изменится на величину a E = + sp I I pq Sq = e p’ q где Ipq – интеграл обменного взаимодействия;

S _p ^Z – оператор спина в узле p .

Учитывая перестановочные соотношения операторов Паули, после применения спектральной теоремы получим выражение для среднего значения оператора числа частиц:

dE =

,           , i +to                     / I \

\^aX) = -I ^fB ^{( E ) lm}\ ^ap|ag/_{E + i9}

^П -to

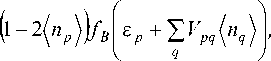
где f _в – функция Бозе–Эйнштейна.

Введем следующее обозначения: na = <^np^ une = ^nq^ — среднее число вакансий, прихо- дящееся на один атом железа в плоскостях α и β cоответственно (α и β – символы четных и нечетных плоскостей в структуре). Получим систему уравнений

( 1 — 2 П a )

n _β

^{- 2} n в ).

= f B ⁽Б + У ^Vn в ),

= f B ⁽ e + Y ^Vn a ) ,

где εα = εβ = ε; γ – координационное число. Тогда для области высоких температур e + y Vn a, в << kT можно записать следующее выражение, производя разложение f β в ряд Тейлора:

n _a = kT n p = kT

.

34,568    9 . (2)

V     V ²

ячейках. Знаки плюс или минус перед корнем в формуле (1) показывают увеличение или уменьшение намагниченности кристалла при упорядочении вакансий. Например, если магнитный момент плоскости β больше магнитного момента плоскости α и вакансии упорядочиваются в плоскости β, то намагниченность образца должна уменьшаться. Если при этом же соотношении магнитных моментов вакансии упорядочиваются в плоскости α, то намагниченность образца должна увеличиваться при увеличении n .

1,2

0,8

0,6

0,4

0,2

0      0,05     0,1

0,15     0,2     0,25

0,3

Потенциал

Р ис. 2. Теоретическая зависимость намагниченности элементарной ячейки от потенциала взаимодействия

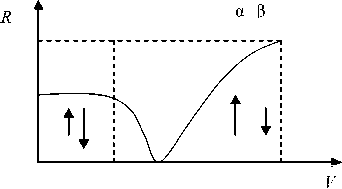
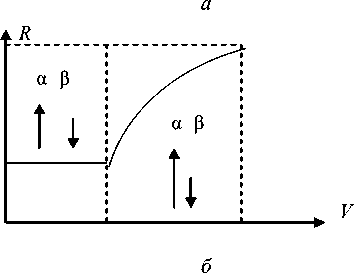
Возможны следующие типы кривых изменения намагниченности в нестехиометрическом ферримагнетике при изменении потенциала взаимодействия вакансий в его структуре (рис. 3):

– тип ферримагнетика, у которого суммарный магнитный момент четных плоскостей β превосходит суммарный магнитный момент нечетных

Обозначим через f , g , k , l узлы первой, второй, третьей и четвертой подрешетки; 1, 2, 3, 4 – величины, относящиеся к первой, второй, третьей и четвертой подрешеткам N i , S i , μ i – число атомов в подрешетке, величину спина и магнитный момент атома сорта i .

R

и

α β

V

-►

в

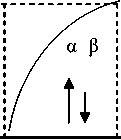
Рис. 3. Теоретические кривые удельной намагниченности β от потенциала взаимодействия V катионных вакансий (обозначения см. в тексте)

В общем случае N 1 * N2 * N3 * N4, S 1 * S2 * S3 * S4, ц1 *ц2 * ^3 *^4,  т.  е. маг— нитные моменты подрешеток различны.

Запишем гамильтониан системы в виде

H =-n t Z [ H S f KZ H S g ) -н з Я H S k ЫК н s l ) - - ^ ^Z I ( f i ^- f 2 ^{) ( S}f , , S f ₂ ^{) - 1} Z I ( ^g 1 ^{- g} 2 ^{) (} S g 1 , S g 2 ^{) - -} 2 К I ^{( k} 1 ^- k 2 ) ( S k 1 , ^Sk ₂ ^)- 2 К I ^{( l}1 ^- l 2 ^{) ( S}l 1 , ^Sl ₂ ^{)- -} Z I ^{( f} - ^{g )(} S f , S g ^)- Z I ^{( k} - ^{l )(} S k , S i ^{)- -} Z I ^{( g - k} ) ( S g , S k ) ^- Z I ⁽ f ^{- k} ) ( ^s/ , S k ^{) -}

-ZI (f - i)(Sf, Si )-Z I (g - i)(Sg, Si), где Sf, Sg, Sk, Sl – спиновые операторы атомов первой, второй, третьей, четвертой подрешеток.

Примем во внимание условие минимума свободной энергии F = -9ln Q, где Q - статистическая сумма, Q = £ e-En /9 = Sp (e - H / &); 9 = kT - мо-n дуль канонического распределения; En – собственные значения гамильтониана H.

Перейдя к операторам S^Z z ,S^zS Z ,S Z ,S ± ,S ± , fgkl fg

S k ,S± и применяя представления Гольштейна -Примакова – Изюмова спиновых операторов через операторы вторичного квантования, получим

S + = 2S ^ ф ( п f "a ^p S f = 2SSa + ф ( п f )

2 S

£ ne - nx где B S = npS^--функция Бриллюэна.

£ e - nx n = 0

Результирующая намагниченность

M ^z = M 1 ^Z + M ₂ ^Z + M ₃ ^Z + M ₄ ^Z ,       (3)

где

M i = NS^^, ,             (4)

Sf = S - nf,

где ф (n f ) =

(

V

^^^^^^s

nf у

2 S J

n f- = a f a f , операто-

ры a ⁺, a удовлетворяют бозевским перестановоч-

ным соотношениям.

Предположив, что в каждой из подрешеток спины ориентированы параллельно друг другу, получим следующую систему уравнений:

где σ – относительная намагниченность на один узел в подрешетке .

Экспериментально получена зависимость намагниченности от температуры нестехиометрических пирротинов состава Fe 10 S 11 , у которых наблюдается возникновение взаимодействия между вакансиями при температуре около 275 °С (рис. 4). Как показано выше, раскомпенсация антиферромагнитных подрешеток зависит от вакансионного взаимодействия. В простейшем случае оно пропорционально температуре. С учетом этого можно увидеть, что подобная зависимость получается естественным образом.

a 1 = ц H + J11S 1 о 1 + J12 S 2 о 2 +

⁺ J 13 ^S 3 ° 3 + J 14 S 4 ° 4 ,

^a 2 = ^ц 2 ^{H +} J 22 ^S 2 ° 2 ⁺ | ^J 121 ^S 1 ° 1 ^{+ +} | ^J ₂ 3 | ^S з ° з + | ^J 24| ^S 4 ° 4 ,

a 3 = ц 3 H + J 33 S 3 ° 3 +1 J ₃₂ | S ₂ ° ₂ +

+ |J 13 |S 1 ° 1 + |J341S4°4 , a4 = ц4H + J44S4°4 + |J42 |S2°2 +

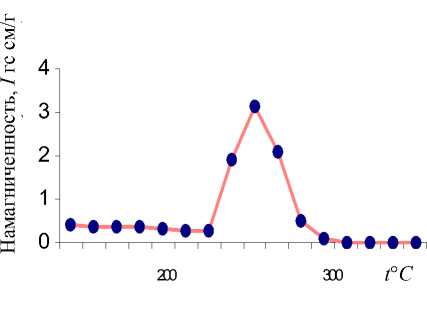
Рис. 4. Экспериментальная зависимость намагниченности от температуры

+ | ^J 43 | ^S 3 ° 3 + | ^J 14 | ^S 1 ° 1 .

Приведенная ниже система уравнений – это и есть искомые уравнения молекулярного поля для четырехподрешеточного изотропного ферримаг-

нетика:

°, = 1 - S ^{- 1} B_s

1            1      S ₁

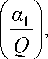
σ ₂

= 1 -

S ^{- 1}B, 2     S ₂

(

V

Or

Q J

σ ₃

= 1 - S 3 ^{- 1} B s 3

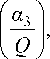
σ ₄

= 1 - S41 Bs

4    S ₄

V

1?)

Q J

Покажем разные типы кривых намагниченности с различным обменным взаимодействием (рис. 5). Заметим, что после перемножения этих кривых с кривой на рис. 2 получается такая же кривая, как и на рис. 4, с учетом того, что потенциал взаимодействия прямо пропорционален температуре, т. е. V = AT . А за счет перемножения же данных кривых с кривыми на рис. 3 получаем воз-можныетипы кривыхнамагниченности нестехиометрических минералов с различным типом расположения катионных вакансий в кристаллической структуре. Сам факт перемножения следует по формулам (3) и (4).

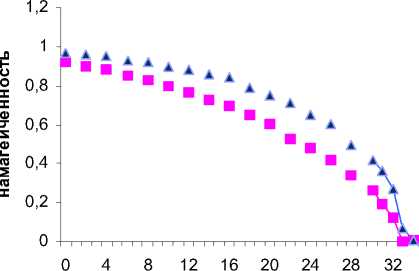
Рис. 5. Кривые намагниченности с различным обменным взаимодействием

Таким образом, в рамках модели четырехпод-решеточного ферримагнетика с учетом взаимодействия между катионными вакансиями, подчиняющимися квантовой статистике Паули, впервые дано теоретическое описание магнитных превращений в нестехиометрических ферримагнетиках. Следует отметить, что появление вакансионного взаимодействия обусловлено, в частности, разрывами связей d -орбиталей (если катионные вакансии образуются в результате удаления ионов железа) и, как следствие, образованием нескомпенсированного электрического заряда на вакантном узле.