Магнитные проводимости двухполюсной реактивной машины с анизотропной магнитной проводимостью ротора

В настоящее время реактивным электрическим машинам с анизотропной магнитной проводимостью ротора уделяется большое внимание, о чем свидетельствует множество статей в иностранных [1–27] и отечественных [28–33] журналах, сборниках и монографиях. Данный класс электрических машин отличает высокий показатель энергетической эффективности [1] и лучшие эксплуатационные характеристики [1, 3–5, 7, 10, 15, 19, 22, 23, 28–33] по сравнению с другими типами электрических машин, включая самую распространенную электрическую машину – асинхронный электродвигатель с короткозамкнутым ротором. Сравнению этих двух классов электрических машин по энергетическим и эксплуатационным характеристикам также посвящено много статей [3, 18, 19, 28–30, 32–35]. Следует отметить, что существуют две технологии изготовления ротора такой электрической машины: с использованием продольной шихтовки пакетов полюса ротора (ALA – Axially Laminated Anisotropic) и поперечной шихтовки пакета ротора со специальными вырезами (TLA – Transversally Laminated Anisotropic). Считается что реактивная машина с поперечной шихтовкой пакета полюса ротора (TLA)

более технологична в изготовлении [5, 22, 23, 33]. В частности, фирма АВВ уже несколько лет промышленно выпускает реактивные электрические машины с поперечной шихтовки пакета ротора (TLA) [34, 35]. На данный момент времени практически все исследования [1–27] посвящены именно реактивной машине с анизотропной магнитной проводимостью ротора с поперечной шихтовкой пакета ротора (TLA). Ряд статей посвящен оптимизации конструкции и геометрических размеров ротора реактивной машины с анизотропной магнитной проводимостью ротора с поперечной шихтовкой пакета ротора (TLA) [5, 8–17, 20, 23–27]. В представленных статьях приводятся в основном результаты численного реже физического моделирования магнитных полей с использованием специализированных программ, основанных на методах конечных элементов, таких как ELCUT, ANSYS Maxwell, Femlab. Несмотря на множество статей и работ, выполненных в последнее время [36–38], посвященных описанию магнитных полей различных типов электрических машин, проведенный анализ показал, что аналитическое описание магнитных проводимостей реактивной машины с анизотропной магнитной проводимостью ротора с продольной шихтовкой пакета ротора (АLA)

отсутствует. Однако по энергетической эффективности реактивная машина с анизотропной магнитной проводимостью ротора с поперечной шихтовкой пакета ротора (TLA) проигрывает реактивной машине с продольной шихтовкой пакетов полюса ротора (ALA) [28, 29, 32]. Далее будем рассматривать только реактивную электрическую машину с продольной шихтовкой пакетов полюса ротора.

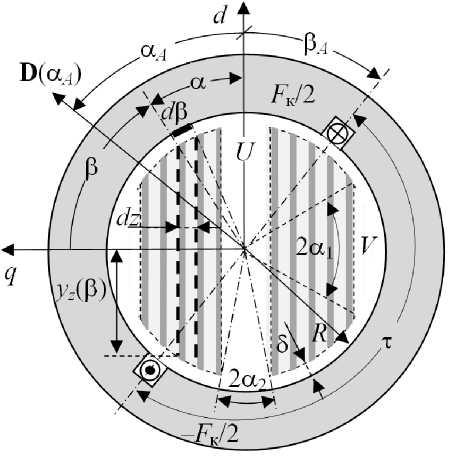
Рис. 1. Магнитная система машины с крепежной выемкой на роторе

Магнитная система реактивной двухполюсной машины с анизотропной магнитной проводимостью ротора изображена на рис. 1. Полагается, что ротор имеет крепежную выемку V и немагнитный промежуток между двумя его половинами U .

Продольная магнитная проводимость двухполюсной машины

При определении продольной магнитной проводимости полагаем, что воздушный зазор в зоне крепежной выемки достаточно велик, и величина крепежной выемки существенно влияет на продольную магнитную проводимость ротора машины. Величина же немагнитного промежутка U на роторе машины дос- таточно мала и не оказывает на продольную магнитную проводимость ротора существенного влияния.

Пусть магнитная проницаемость ротора машины в продольном направлении равна бесконечности, а поперечном направлении – нулю. Тогда функция магнитного потенциала ротора запишется в виде:

U r ( в , a A )

1/2 при ве [0, » i ] и ве [ a ₁, a A ];

0 при ве[аA, п /2], где в — текущий угол, отсчитываемый от оси q; aA - угол, характеризующий положение магнитной оси катушки A; a1 - половина углового размера крепежной выемки.

В этом случае катушка с током двухполюсной машины будет порождать в воздушном зазоре продоль- ное магнитное напряжение

F d ( в , a A )

0 при в е [0, a ₁] и Pe [ a 1 , a A ];

1/2 при a ₁, a A < в < п /2,

где в , a a е [0, п /2].

Продольное магнитное напряжение в воздушном зазоре (1) может быть представлено двойным рядом Фурье

ГО го

F S d ^{( в} , ^a A ) = EE F d ( u , V ) ■ co^{s( u} ■ ^a A ) ■ ^sin( v ■ ^{в )} ,                                                            ⁽²⁾

• i = 1 j = 1

где

• о п/2 п/2

F Sd ( u , v ) = — ■ J J ^cos( v -P ) ■ d P- ^sin( u -P ) ■ d P                                                                (3)

• ^п 0 a A

  - амплитуда гармоники порядка и = 2 ■ i - 1, v = 2 ■ j - 1 продольного магнитного напряжения в воздушном

зазоре.

После интегрирования выражения (3), амплитуда гармоники порядка u, v продольного магнитного на- пряжения запишется в виде:

_ 2    Г sin( x ■ k_v ) - sin( x ) sin( y ■ k_v ) - sin( y )

F S d ( и , v ) =          I

• y - x ( x               y

где x = ( v - и )- п /2; y = ( v + и )- л /2; k_v = 2- a 1 / n - доля, занимаемая крепежной выемкой на угловом полюсном делении.

Взаимная относительная продольная магнитная проводимость катушек A и B, в соответствии с формулой ав+п

B

X ( a a , а в ) = Х ( a в , a a ) = -■ f F S ( р , a a ) ■ d р ,                                                          (5)

а в определится выражением:

**

^ dd ^{( а} A , ^a B ) = ^ ^{( а} B , ^а A )

^а B ^+л                       от от

■ J F S d Ф, ^а A ) ■ ^d Р = ЕЕ ^Л * dd ( и , v ) ■ co^s((2 ■ ^{и - 1)} ^^a A ) ■ c^os((2 ■ ^{v -} 1) ^^a B ), (6)

a _в                        и = 1 v = 1

где

*2

^Л dd ( и , v ) = ^П

sin( x ■ k_v ) - sin( x )  sin( y ■ k_v ) - sin( y )

----------------Z---------Z---Z---------Z--------- ^x ■ ^{( x 2 -} y 2 )          y ■ ^{( x 2 -} y ²⁾

– относительная продольная магнитная проводимость.

Так как при x = 0 в выражении (7) имеет место неопределенность, то взаимную относительную продольную магнитную проводимость катушек A и B удобнее вычислять по формуле

< " dd ^{( a} a ^{, a} в

от Г

E a *

^Л dd ( v , v )

i = 1 1

v -1   *

■ C°S ^{( v} ^^a A ) ■ C°S ^{( v} ■^a B ) + ² 'E ^ dd ( и v ) ■ ^{cos( и} ^^a A ) ■ ^{cos( v} ^^a B )

j = 1                                          J

где

. *           1 Г, , sin( v ■ n ■ k, /2)

^Л dd ( v , v ) = — ■ I ^{1 -} k v ⁺ —----— ’ v ² k                v ■n

– амплитуда гармоники порядка v , v относительной продольной магнитной проводимости.

При круглом основании цилиндрического ротора (kv = 0) продольное магнитное напряжение в воздушном зазоре (2) может быть представлено простым рядом Фурье от

F S d ⁽ P , ^a A ) = E F s d ( v ) ■ ^{cos( v} ■ ^a A ) ■ ^{sin( v} ■ ^{e )} , j = 1

где

F s d ( v ) = —                                                                             (10)

n^ v

– амплитуда гармоники продольного магнитного напряжения в воздушном зазоре порядка v . График функции продольного магнитного напряжения в воздушном зазоре приведен на рис. 2, б .

Взаимная относительная продольная магнитная проводимость катушек A и B у машины c круглым основанием цилиндрического ротора может быть также представлена простым рядом Фурье.

^ * dd ⁽ a A , a в ) = Е ^Л * dd ( v ) ■ cos⁽ v ■a a ) ■ cos⁽ v ■a в )                                                         ⁽¹¹⁾

j = 1

где

^Л dd ( v ) =^Л dd ( v , v ) = ~                                                                                      ⁽¹²⁾

v

– амплитуда гармоники порядка v относительной продольной магнитной проводимости.

Амплитуда гармоники порядка u, v = 1 продольной магнитной проводимости совпадает с базовой маг нитной проводимостью Лdd(1,1) и называется основной продольной магнитной проводимостью

4 ■ Un ■ l ■ т

^Л dd =^Л dd (1,1) =^Л б =     2~Т* ,                                                                                ⁽¹³⁾

П ■S где S = S/R - относительный расчетный воздушный зазор между статором и ротором; т = л/р - угловое полюсное деление; р – число пар полюсов; l – длина магнитопровода.

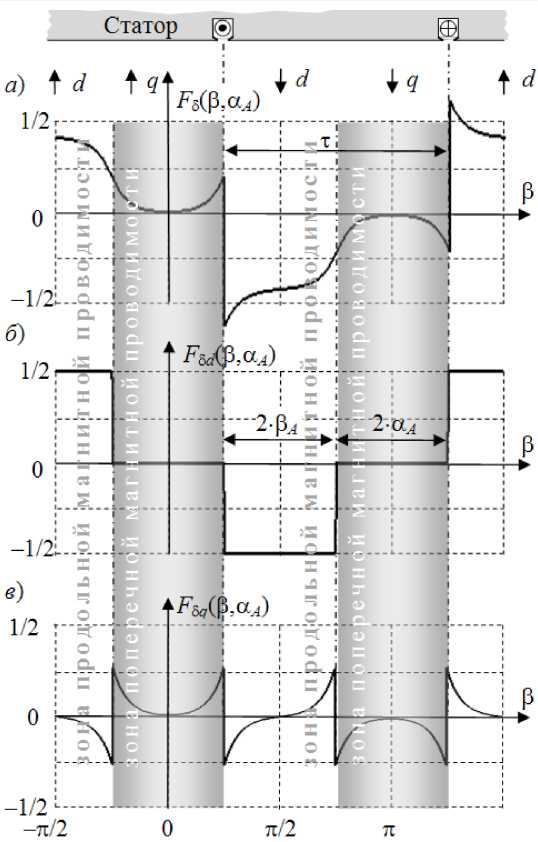
Рис. 2. Графики функций магнитного напряжения в воздушном зазоре при круглом основании цилиндра ротора: а – суммарного; б – продольного; в – поперечного

Основная удельная продольная магнитная проводимость c круглым основанием цилиндрического ро-

тора

Λ

o

dd =

Λ dd µ ₀ ⋅ l

4 р ⋅π⋅δ ^*

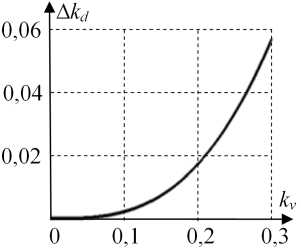
Рис. 3. Зависимость коэффициента вариации продольной магнитной проводимости от ее доли на угловом полюсном делении

Для оценки влияния крепежной выемки на продольную магнитную проводимость катушки введем понятие коэффициента вариации продольной магнитной проводимости , обусловленной крепежной выемкой

Δkd=1-Λ*dd= kv-sin(kv⋅π), (15) π где kv = 2·α1/π – доля, занимаемая крепежной выемкой на угловом полюсном делении τ; α1 – половина геометрического углового размера крепежной выемки. Коэффициент вариации продольной магнитной проводимости показывает, насколько крепежная выемка уменьшает продольную магнитную проводимость

Λdd =Λб⋅(1-∆kd), где Λб – базовая магнитная проводимость (13). Зависимость коэффициента вариации продольной магнитной проводимости от ее доли на угловом полюсном делении приведена на рис. 3.

Поперечная магнитная проводимость двухполюсной машины

Поперечное магнитное напряжение в воздушном зазоре можно записать в виде составной функции:

0 при р е [0, а 1 ];

F> q ( в , а a ) = F ₅ ( р , а a ) - F _{5 d} ( р , а a ) = 1 1/2 - U Rq ( в ) при ре [ a i , a a ]; [- U Rd ^{( в )} при ^{ре [ а} a , п /2^],

где

U Rd ( в ) = C d • cosh( c • в ) + C 2 d • sinh( c • в );

URq (в) = 2 — Ciq • cosh(C • в) — c2q • smh(c • в), где URd(в) и URq(в) — функции магнитного потенциала ротора в зоне продольной и поперечной проводимости.

С учетом соотношений (17) поперечное магнитное напряжение в воздушном зазоре

0 при в е [0, а 1 ];

^F 5 q ^{( в} , ^а A ) = 1 ^C 1 q • c^Osh( C • ^{в ) + C} 2 q ' s^{inh( C} ' ^{в )} при ^{в е [ a} 1 , ^a A L

- C1 d • cosh(c • в) - C2d • sinh(c • в) при в е [aA, п /2], где с – коэффициент затухания магнитного потенциала многополюсной машины, характеризующий скорость уменьшения функций поперечного потока и магнитного потенциала ротора в зоне поперечной магнитной проводимости по мере удаления от паза с проводниками катушки, определяемый как с = 1J^pq -5* ; pq* - относительная поперечная магнитная проницаемость полюса ротора; 5* - относительная величина расчетного воздушного зазора. График функции поперечного магнитного напряжения в воздушном зазоре при a1 = 0 приведен на рис. 2, в.

Поперечное магнитное напряжение в воздушном зазоре (18) может быть представлено двойным рядом Фурье

ГО го

F 5 q ^{( в} , ^a A ) S S ^F 5q ( u , v ) • ^sin( v • ^a A ) • ^cos( u • ^{в )} ,                                                               ⁽¹⁹⁾

i = 1 j = 1

где

1 z- п/2 п/2

F 5q ( u , v ) = — • J J ^F 5 q ^{( в} , ^a A ) • c^os( u • ^{в )} • ^{d в} • ^sin( v • ^{в )} • ^{d в П} 0 a A

– амплитуда гармоники порядка u , v поперечного магнитного напряжения в воздушном зазоре.

Амплитуда гармоники порядка u = v = 1 поперечного магнитного напряжения в воздушном зазоре запишется в следующем виде:

_ 2 ^f 1 - k_v sin( k v ■ п ) c ² - 1        4 • c

^{5 q (1,1)} п ^ c ² + 1 п       ( c ² + 1)² л^ ( c ² + 1)²

I Orr      f _ „ . Ck, • п^ । Orr • C + S . q f k • п^ 11

X --- U--C - 2 • sin ——   + —-- sin ² ——   ,

(aU • S + C (        ( 2 JJ OU • S + C ( 2 JJJ kv - доля, занимаемая крепежной выемкой на угловом полюсном делении; aU = 2 ^pq / 5* / XU - коэффи- циент магнитного сопротивления между полюсами ротора;

S = sinh

^{c (1 -} k v ) 2

C = cosh

^{c (1 -} k v ) 2

Взаимная относительная поперечная магнитная проводимость катушек A и B, в соответствии с формулой (5), определяется выражением aB+п                       го го

п

^X qq ^{( a} A ^{, a} B ) = J^ J ^F 5 q ^{( в} , ^a A ) • ^{d в} = SS ^Л qq ( u , v ) ^ si^{n(( U} ^ A ) • sⁱⁿ⁽⁽ v ^ B ),                        ⁽²³⁾

⁴ a _B                         i = 1 j = 1

где F _{5 q} ( в , a _A ) - поперечное магнитное напряжение в воздушном зазоре (18).

Амплитуды гармоники порядков u , v относительной поперечной магнитной проводимости катушек при u ^ v могут быть вычислены по приближенным формулам:

*          1 — k_v    sin(2 ■ v ■aj ■ ( v ² — c ²)

^Л qq ( v . v ) ~ 2 , 2⁺           / 2 , 2^2

v + c       v -n- ( v + c )

—

4 ■ c

n ( v ² + c 2 ) 2

(                    ^

sin²( v ■«J + — U- I ;

I              1 + ° и J

*

Л / A ® qq ( u , v )

— 2 ( 2 ■ sin(2 ■ v ■aj■ sin(2 ■ u -а 1 )   ( u ■ v — c 2 ) ■ sin(( u + v ) -« 1 )   ( u ■ v + c 2 ) ■ sin(( u — v ) -« 1 )

( u ² + c ²) ■ ( v ² + c ²)        ( u + v ) ■ ( u ² + c ²) ■ ( v ² + c ²) ( u — v ) ■ ( u ² + c ²) ■ ( v ² + c ²)

—

)

■ . (25)

Приближение получено путем предельного перехода при exp( n c ) ^ да . Погрешность формулы при c > 1,3 и u , v > 3 не превышает 5 %.

Взаимную относительную поперечную магнитную проводимость катушек A и B удобнее вычислять по формуле да (

***

^ qq ⁽ « A , « B ) = L I ^Л qq ( v , v ) ‘ sin⁽ v ‘ « A ) ‘ sin⁽ v ‘ « B ) ^{+ 2} ' L ^Л qq ( u , v ) ‘ sin⁽ u ‘ « A ) ‘ sin⁽ v ‘ « B )

j=1 t

Основная относительная поперечная магнитная проводимость (амплитуда гармоники порядка u , v = 1)

*      *

Л qq = Л qq (1,1) = 2 " Fq (1,1) , где F5q(i,i) - амплитуда гармоники порядка u = v = 1 поперечного магнитного напряжения в воздушном зазоре.

При круглом основании цилиндрического ротора ( k_v = 0; a _U = 0) поперечное магнитное напряжение в воздушном зазоре может быть представлено простым рядом Фурье да

F 5 q Ф, ^a A ) = L F 5 q ( v ) ■ ^sin( v ■ ^a A ) ■ co^s( v ■ ^{e )} ,                                                                    ⁽²⁷⁾

j = 1

где

F 5 q ( v )    _

П

v

■ 2,2 v + c

– амплитуда гармоники поперечного магнитного напряжения в воздушном зазоре. График функции поперечного магнитного напряжения в воздушном зазоре приведен на рис. 2, в .

Взаимная относительная поперечная магнитная проводимость катушек A и B у машины c круглым основанием цилиндрического ротора может быть представлена простым рядом Фурье да

^ qq ^{( a} A ^{, a} B ) = L ^Л qq ( v ) ■ sin⁽ v ■« A ) ■ sin⁽ v ■« B ),                                                           (29)

k = 1

где

Л *

qq ( v )

= Л *

qq ^{( v} ’ ^v ) = _v 2 _{+ c} ²

– амплитуда гармоники порядка v поперечной относительной магнитной проводимости. Амплитуда гармоники порядка v поперечной магнитной проводимости

X             *    -   ^Л б

^Л qq ( v ) = ^Л б ^Л qq ( v ) = ₂ ,   2 ^.

v + c

Коэффициент поперечной магнитной проводимости с учетом крепежной выемки и межполюсного немагнитного промежутка является важным показателем характеризующим эффективность работы реактивной электрической машины. Он определится выражением kq = kq (kv , Hu ) =4qq = Fq1^ .                                                            (31)

^Л dd F 5 d (1,1)

Для оценки влияния крепежной выемки и межполюсного немагнитного промежутка на основную поперечную магнитную проводимость катушки введем понятие коэффициента вариации поперечной магнитной проводимости, обусловленной крепежной выемкой и межполюсным немагнитным промежутком

A k = 1 — (1 + c ²) ■Л * = 1 — k q ⁽ k v ’ ° ^U ) .                                                                   (32)

^{q                   qq}        k q (0,0)

Поперечная магнитная проводимость основной гармоники с учетом крепежной выемки и межполюсного немагнитного промежутка между полюсами ротора

• 1    — A k„

Л qq =Л б ■         .                                                                                    (33)

• 1 + c ²

Положим, что межполюсный немагнитный промежуток отсутствует (aU = 0). Тогда коэффициент вариации поперечной магнитной проводимости, обусловленной влиянием крепежной выемки, определится выражением

А k qV = 1

k q ( k v ,0) k q (0,0)

sin( k v - л) c ² - 1      4 • c

kv----5--1--5------ n     c2 +1  П (c2 + 1)

• sin²

k v -n

• tanh

( c    ⁽1 ^- k v ) )

I ²       )

где k v = 2* a ₁Z n - доля, занимаемая крепежной выемкой на угловом полюсном делении; c - коэффициент затухания. Зависимость коэффициента вариации поперечной магнитной проводимости, обусловленной крепежной выемкой, от ее доли на угловом полюсном делении приведена на рис. 4, а .

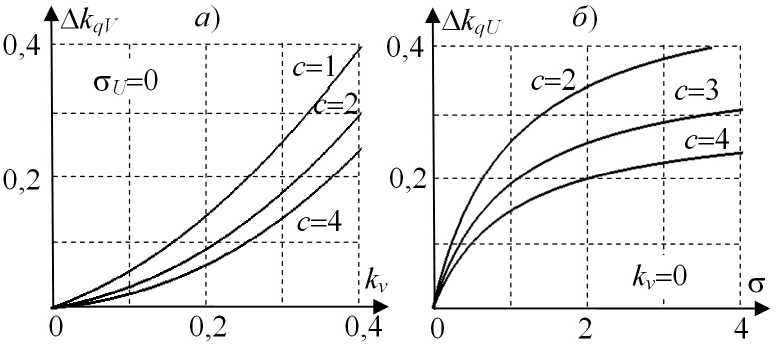
Рис. 4. Зависимости коэффициента вариации поперечной магнитной проводимости двухполюсной машины: а – обусловленной крепежной выемкой, от её доли на угловом полюсном делении; б – обусловленной межполюсным воздушным промежутком, от коэффициента магнитного сопротивления между полюсами ротора

Из приведенных графиков рис. 4 следует, что крепежная выемка и межполюсный немагнитный промежуток уменьшают поперечную магнитную проводимость катушки и коэффициент поперечной магнитной проводимости.

Положим, что крепежная выемка отсутствует ( k_v = 0). Тогда коэффициент вариации поперечной магнитной проводимости, обусловленный влиянием межполюсного немагнитного промежутка:

^{А k} qU

^k q ⁽⁰, ^a U ) k q (0,0)

______________ ⁴ • c ^^a U ______________ n • (1 + c ² ) • (1 + a U • tanh( c • n Z 2))

Зависимость коэффициента вариации поперечной магнитной проводимости, обусловленной межполюсным воздушным промежутком, от коэффициента магнитного сопротивления между полюсами ротора представлена на рис. 4, б .

Используя полученные выражения, можно определить величину коэффициента поперечной магнитной проводимости для реактивной электрической машины с продольной шихтовкой ротора (АLA) и сравнить полученное значение с значением коэффициента поперечной магнитной проводимости для реактивной электрической машины с поперечной шихтовкой ротора (ТLA). Такое сравнение позволяет оценить энергетическую эффективность различных технологий изготовления ротора таких электрических машин. Результаты сравнения приведены в таблице.

Результаты сравнения реактивной электрической машины с продольной шихтовкой ротора (АLA) и с поперечной шихтовкой ротора (TLA)

Тип реактивной электрической машины	k q
С продольной шихтовкой ротора (АLA)	0,03…0,05
С поперечной шихтовкой ротора (TLA)	0,08…0,14

Заключение

Полученные аналитические зависимости являются новыми, нигде ранее не встречавшимися в научной литературе, и позволяют определить магнитные проводимости двухполюсной реактивной электрической машины с продольной шихтовкой ротора (АLA). Из представленных зависимостей и графиков следует, что крепежная выемка и межполюсный воздушный промежуток существенно уменьшают поперечную магнитную проводимость машины, а следовательно, улучшают ее эффективность. Показано, что по энергетическим характеристикам реактивная машина с анизотропной магнитной проводимостью ротора с продольной шихтовкой пакетов полюса ротора (ALA) выигрывает у реактивной машины с поперечной шихтовкой пакета ротора (TLA). Полное математическое описание и результаты исследования, приведенные в данной статье, использованы при написании методики проектирования синхронной электрической машины с анизотропной магнитной проводимостью ротора [31]. Предложенное математическое описание магнитных проводимостей может быть полезно при проектировании и оптимизации конструкции реактивной электрической машины с анизотропной магнитной проводимостью ротора. Представленные результаты будут полезны широкому кругу специалистов, а также проектантам электроприводов на основе реактивных электрических машин с анизотропной магнитной проводимостью ротора с продольной шихтовкой пакетов полюса ротора (ALA).