Магнитоемкость в сульфидах марганца с редкоземельным замещением Mn1-xRexS

В космических аппаратах электроника функционирует в экстремальных условиях с перепадом температур в сотни градусов. Необходимо найти материалы, например, на основе мульти-ферроиков, которые смогут проявить стабильность работы в этих условиях.

Материалы, в которых проявляется взаимосвязь магнитных и электрических свойств, магнитоэлектрики и мультиферроики, представляют интерес как с фундаментальной, так и с прикладной точек зрения [1–4]. Особое внимание привлекают материалы, обнаруживающие магнитоэлектрические свойства в области комнатных и более высоких температур в связи с практическим применением в микроэлектронике для записи и хранения информации [5; 6]. К таким изученным материалам относится феррит висмута BiFeO3 [7–9]. Эффект гигантской магнитоемкости наблюдается в LuFe2O4 при комнатной температуре и объясняется флуктуацией заряда с разной величиной спина в ионах Fe2+ и Fe3+ в результате снятия вырождения между двумя типами зарядового порядка внешним магнитным полем [10].

Магнитоемкость в электрически неоднородной среде может быть обусловлена эффектом Максвелла – Вагнера [11–14] в результате тензорного характера взаимодействия носителей тока с магнитным и электрическим полем и смешивания продольных и поперечных компонент проводимости. В модели магнитоемкость положительна при условии, что размер электрической неоднородности на порядок превышает длину свободного пробега электрона, время измерения 1/ω превышает время рассеяния и матрица является диэлектрической [13].

Такие эффекты ясно демонстрируют, что наличие магнитоемкости не достаточно для отнесения этих соединений к мультиферроикам. С другой стороны, магнитоемкость без магнитоэлектрической связи может быть более практичной для технологических применений, так как не требуется существование дальнего магнитного порядка.

Диэлектрическая проницаемость и ее отклик на магнитное поле зависят от степени электрической неоднородности, которую можно менять в результате нестехиометрического замещения в сульфиде марганца, например, ионами гадолиния с нулевым орбитальным магнитным моментом и тулия, орбитальный момент которого обуславливает электрическую поляризуемость иона [15–19]. Кроме того, ион иттербия относится к элементам с переменной валентностью [20–23], флуктуации валентности которого дадут дополнительный вклад в диэлектрическую проницаемость и импеданс [24–26].

Цель исследования – установить влияние катионного замещения на электрическую поляризацию, отклик диэлектрических характеристик и диэлектрических потерь на магнитное поле при электронном допировании полупроводников.

Рентгеноструктурный анализ и методика

Исследовались поликристаллические образцы Mn1-xGdxS и Mn1-xYbxS c концентрацией x = 0,2, вблизи концентрации протекания ионов по ГЦК решетки. Согласно рентгеноструктурным данным, образцы имеют ГЦК тип решетки, аналогичный исходным сульфидным соединениям [27]. На рис. 1 представлена рентгенограмма образцов.

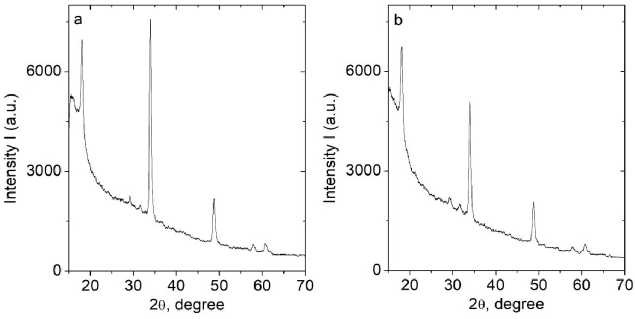
Рис. 1. Рентгеновская дифракционная картина образцов Mn_0,85Yb_0,15S ( a ) и Mn_0,8Yb_0,2S ( b ) при комнатной температуре

Fig. 1. X-ray diffraction pattern of Mn_0.85Yb_0.15S ( a ) and Mn_0.8Yb_0.2S ( b ) samples at room temperature

Сульфид гадолиния имеет металлический тип проводимости, сульфид иттербия относится к полупроводникам со щелью в спектре электронных возбуждений. Под действием внешнего давления щель закрывается и YbS проявляет металлические свойства. С ростом числа электронов незаполненные 4 f уровни ближе перемещаются к энергии Ферми, что приводит к изменению электронных свойств. Смещение 4 f уровня к энергии Ферми происходит в тяжелых редкоземельных элементах от GdS к YbS, где 4 f уровень пересекает дно зоны и находится в запрещенной щели [28–32].

Диэлектрическая проницаемость и диэлектрические потери определены из измерения емкости и тангенса угла потерь, измеренных на приборе AM-3028 анализатор компонентов в диапазоне частот 102–106 Гц при температурах 80–500 К. Магнитоемкость δ(Re(ε)) и диэлектрические потери в магнитном поле образца определялись как

δ (Re( ε )) =

(Re( ε ( H )) - Re( ε (0)))

Re( ε (0))        ^;

_{δ (Im( ε )) =} (Im( ε ( H )) - Im( ε (0)))

Im( ε (0))

где Re( ε ( H )) и Im( ε ( Н )) – действительная и мнимая части диэлектрической проницаемости образца в магнитном поле Н = 12 кЭ, приложенном параллельно обкладкам конденсатора, а Re( ε (0)) находится в нулевом магнитном поле. Для предотвращения токов утечки между образцом и обкладками конденсатора помещался слой слюды толщиной несколько микрометров.

Результаты и обсуждения

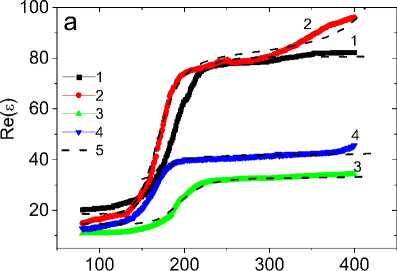
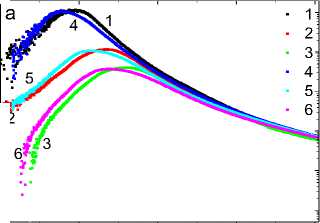
На рис. 2 приведены компоненты диэлектрической проницаемости от температуры для Mn0.8Yb0.2S. В интервале температур 160–180 К диэлектрическая проницаемость резко возрастает, а диэлектрические потери имеют максимум, который смещается от Т = 166 К к T = 190 К c увеличением частоты от 10 до 100 кГц. При нагревании диэлектрическая проницаемость в магнитном поле увеличивается выше 170 К (рис. 2, b), диэлектрические потери также возрастают в несколько раз. Рост диэлектрических потерь может быть вызван увеличением времени релаксации либо ростом проводимости в магнитном поле. Измерение активной и реактивной компонент импеданса частично отвечает на этот вопрос.

T, K

c

л* А !

е"

100     200     300     400

T, K

—■—1

—•—2

—▲—3

—▼—4

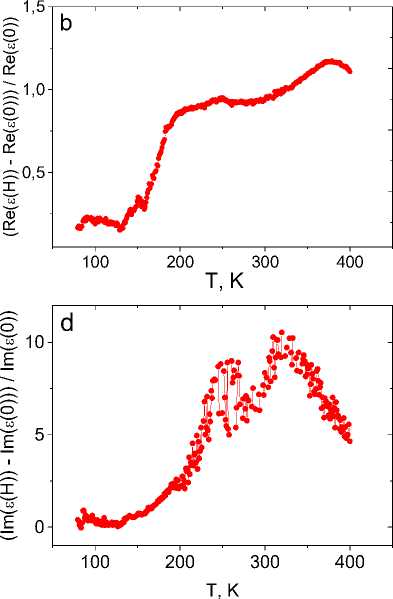
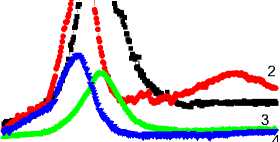
Рис. 2. Температурная зависимость действительной части диэлектрической проницаемости для образца Mn_0,8Yb_0,2S, измеренная в нулевом магнитном поле на частотах 100 кГц ( 3 ), 10 кГц ( 4 ) и в магнитном поле H = 8 кЭ на частотах 100 кГц ( 1 ), 10 кГц ( 2 ). Теоретические расчеты в модели Дебая – пунктирные линии 5 ( a ). Относительное изменение действительной части диэлектрической проницаемости в магнитном поле H = 8 кЭ на частоте 10 кГц ( b ). Температурная зависимость мнимой части диэлектрической проницаемости для образца Mn_0,8Yb_0,2S, измеренная в нулевом магнитном поле на частотах 100 кГц ( 3 ), 10 кГц ( 4 ) и в магнитном поле H = 8 кЭ на частотах 100 кГц ( 1 ), 10 кГц ( 2 ) ( с ). Относительное изменение мнимой части диэлектрической проницаемости в магнитном поле H = 8 кЭ на частоте 10 кГц ( d )

Fig. 2. Temperature dependence of the real part of the dielectric constant for the Mn_0.8Yb_0.2S sample measured in a zero magnetic field at frequencies 100 kHz ( 3 ), 10 kHz ( 4 ) and in a magnetic field H = 8 kOe at frequencies 100 kHz ( 1 ), 10 kHz ( 2 ). Theoretical calculations in the Debye model – dotted lines 5 ( a ). Relative change in the real part of the dielectric constant in a magnetic field H = 8 kOe at frequency 10 kHz ( b ). Temperature dependence of the imaginary part of the dielectric constant for the Mn_0.8Yb_0.2S sample measured in a zero magnetic field at frequencies 100 kHz ( 3 ), 10 kHz ( 4 ) and in a magnetic field H = 8 kOe at frequencies 100 kHz ( 1 ), 10 kHz ( 2 ) ( с ). Relative change in the imaginary part of the dielectric constant in a magnetic field H = 8 kOe at frequency 10 kHz ( d )

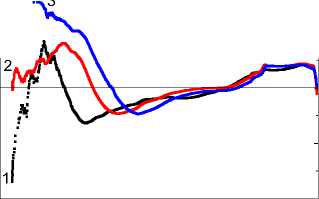
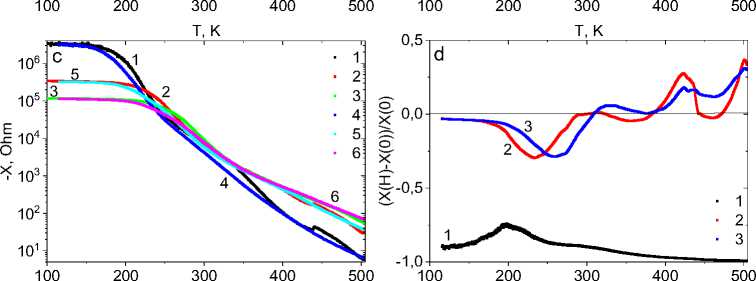
На рис. 3 представлены зависимости сопротивления на переменном токе и реактивного сопротивления без магнитного поля и в магнитном поле. Максимум сопротивления R(T) в магнитном поле смещается в область низких температур. В результате магнитосопротивление в области температур 160–400 К меняет знак и становится отрицательным. Реактивное сопротивление уменьшается в два раза на частоте 10 кГц по абсолютной величине. Соединение Mn 0,8 Yb 0,2 S имеет большое сопротивление и реактивное сопротивление X = Lω – 1/ωC обусловлено в основном емкостью. Уменьшение X(H) / X(H = 0) вызвано увеличением емкости, что согласуется с магнитоемкостью (рис. 2, b ).

Е 104

°    2

± 103

и:

и:

1,0

b

0,5

0,0

-0,5

-1,0

T, K

T, K

Рис. 3. Температурная зависимость активного сопротивления для образца Mn_0,8Yb_0,2S без поля ( 1 , 2 , 3 ) и в магнитном поле ( 4 , 5 , 6 ) на частотах 10 кГц ( 1 , 4 ), 100 кГц ( 2 , 5 ), 300 кГц ( 3 , 6 ) ( a ). Магнитосопротивление активной части импеданса от температуры на частотах 10 кГц ( 1 ), 100 кГц ( 2 ), 300 кГц ( 3 ) ( b ). Зависимость реактивного сопротивления от температуры без поля ( 1 , 2 , 3 ) и в магнитном поле ( 4 , 5 , 6 ) на частотах 10 кГц ( 1 , 4 ), 100 кГц ( 2 , 5 ), 300 кГц ( 3 , 6 ) ( c ). Магнитосопротивление реактивной части импеданса от температуры на частотах 10 кГц ( 1 ), 100 кГц ( 2 ), 300 кГц ( 3 ) ( d )

Fig. 3. Temperature dependence of active resistance for the Mn_0.8Yb_0.2S sample without a field ( 1 , 2 , 3 ) and in a magnetic field ( 4 , 5 , 6 ) at frequencies 10 kHz ( 1 , 4 ), 100 kHz ( 2 , 5 ), 300 kHz ( 3 , 6 ) ( a ). Magnetoresistance of the active part of the impedance versus temperature at frequencies 10 kHz ( 1 ), 100 kHz ( 2 ), 300 kHz ( 3 ) ( b ). Dependence of reactance on temperature without a field ( 1 , 2 , 3 ) and in a magnetic field ( 4 , 5 , 6 ) at frequencies 10 kHz ( 1 , 4 ), 100 kHz ( 2 , 5 ), 300 kHz ( 3 , 6 ) ( c ). Magnetoresistance of the reactive part of the impedance versus temperature at frequencies 10 kHz ( 1 ), 100 kHz ( 2 ), 300 kHz ( 3 ) ( d )

Качественное отличие X(H)/X(H = 0) и С(Н)/C(H = 0) на высоких частотах ω > 105 Гц обусловлено появлением индуктивного вклада электронов в окрестности ионов иттербия. Перескоки электронов около примесного центра способствуют появлению орбитального магнитного момента и их синхронизации во внешнем магнитном поле. На низких частотах добавляется диффузионный вклад, который найден из спектра импеданса. В сульфидах марганца, замещенных элементами с переменной валентностью, наблюдаются большие диэлектрические потери, обусловленные локальной деформацией вблизи ионов иттербия при флуктуациях валентности. Диэлектрические потери вызваны электрон-фононным взаимодействием носителей тока с фононами. Мнимая часть диэлектрической проницаемости связана с действительной частью оптической проводимости σ' соотношением Im(ε) = σ'/ω. В неупорядоченных полупроводниках с прыжковым типом проводимости может реализоваться резонансный и релаксационный механизм проводимости.

Замещение марганца гадолинием качественно не меняет зависимостей ε(Т), представленных на рис. 4. Диэлектрическая проницаемость Mn 0,8 Gd 0,2 S растет при нагревании и имеет перегиб при 170 К. Магнитоемкость уменьшается на порядок в Mn 0,8 Gd 0,2 S по сравнению с Mn 0,8 Yb 0,2 S.

Для состава Mn0.8Gd0.2S диэлектрическая проницаемость обусловлена локализованными электронами в подрешетке ионов марганца и электронами проводимости в гадолиневой подсистеме. Мнимая часть диэлектрической проницаемости Im(ε(ω)), приведенная на рис. 5, имеет два максимума при Т = 170 К и Т = 442 К. Низкотемпературный максимум сдвигается в маг- нитном поле Н = 8 кЭ в сторону высоких температур (рис. 5). Диэлектрические потери уменьшаются в магнитном поле, кроме температурной области 194–279 К и 417–451 К (рис. 5). Низкотемпературный максимум в Im(ε(ω)) при Т = 170 К опишем в модели локализованных электронов с замерзанием дипольных моментов с энергией активации ΔE = 900 К без магнитного поля и в магнитном поле ΔE = 1050 К.

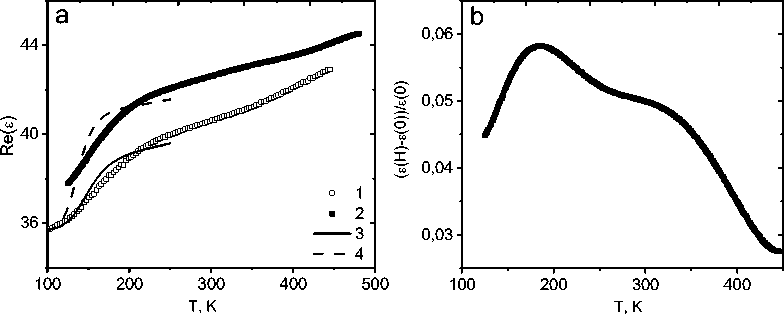
Рис. 4. Действительная часть диэлектрической проницаемости ( а ) от температуры для твердого раствора Mn_0,8Gd_0,2S, измеренная на частоте 10 кГц без поля ( 1 ) и в магнитном поле Н = 8 кЭ ( 2 ). Подгоночная функция Re(ε) = A/(1 + Bexp(2ΔE/T)) + ε₀ c энергией активации ΔE = 900 К ( 3 ), 1050 К ( 4 ) ( a ). Магнитоемкость в магнитном поле H = 8 кЭ от температуры ( b )

Fig. 4. Real part of the dielectric constant (a) on temperature for Mn_0.8Gd_0.2S solid solution, measured at a frequency of 10 kHz without a field ( 1 ) and in a magnetic field H = 8 kOe ( 2 ). Fitting function Re(ε) = A/(1 + Bexp(2ΔE/T)) + ε 0 with activation energy ΔE = 900 K ( 3 ), 1050 K ( 4 ) ( a ). Magnetic capacity in a magnetic field H = 8 kOe depending on temperature ( b )

Подгоночная функция

Im (ε) = A 1 ·exp(ΔE / T) / (1 + B·exp(2ΔE / T)); Re(ε) = ε 0 + C / (1 + B·exp(2ΔE / T))     (2)

хорошо описывает экспериментальные данные на рис. 4 и 5 в интервале температур 100–250 К.

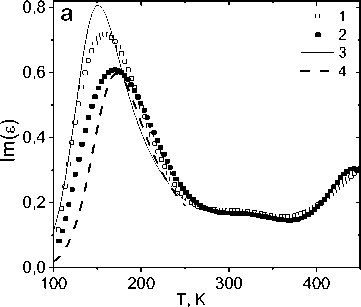
Рис. 5. Мнимая часть диэлектрической проницаемости ( а ) от температуры для твердого раствора Mn_0,8Gd_0,2S, измеренная на частоте 10 кГц без поля ( 1 ) и в магнитном поле Н = 8 кЭ ( 2 ) Подгоночная функция с энергией активации 900 К ( 3 ), 1050 К ( 4 ) ( a ). Относительное изменение мнимой части диэлектрической проницаемости в магнитном поле от температуры ( b )

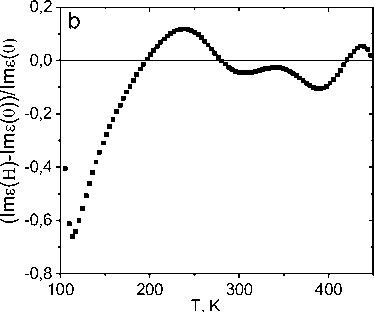
Fig. 5. Imaginary part of the dielectric constant ( a ) on temperature for Mn_0.8Gd_0.2S solid solution, measured at a frequency of 10 kHz without a field ( 1 ) and in a magnetic field H = 8 kOe ( 2 ). Fitting function with activation energy 900 K ( 3 ), 1050 К ( 4 ) ( a ). Relative change in the imaginary part of the dielectric constant in a magnetic field on temperature ( b )

Максимальное уменьшение диэлектрических потерь в магнитном поле наблюдалось в окрестности температуры Нееля и вызвано уменьшением рассеяния заряженных частиц на спиновых флуктуациях, которые подавляются магнитным полем. Рост диэлектрической проницаемости выше комнатной температуры вызван ростом радиуса делокализации электронов и исчезновением орбитально-зарядового упорядочения.

Диэлектрическая проницаемость Mn_0,8Yb_0,2S описывается формулой (2) в модели Дебая c активационной зависимостью времени релаксации τ с = τ 0 ·exp(ΔE / kT), где ΔE – энергия активации (ΔE = 0,17 эВ).

Заключение

Замещение ионов марганца редкоземельными ионами в области протекания приводит к существенному отличию диэлектрических свойств. Наличие ионов переменной валентности приводит к увеличению диэлектрической проницаемости в два раза и диэлектрических потерь на порядок по сравнению с Mn0.8Gd0.2S. Это вызвано флуктуацией валентности и сильной элек-трон-решеточной связью. При переходе в антиферромагнитное состояние диэлектрические потери уменьшаются в магнитном поле в два раза в Mn0.8Gd0.2S и не меняются Mn0.8Yb0.2S. Выше комнатной температуры мнимая часть диэлектрической проницаемости увеличивается на порядок в Mn0.8Yb0.2S. Уменьшение реактивного сопротивления в Mn0.8Yb0.2S в магнитном поле при низких частотах вызвано ростом емкости, а на высоких частотах – ростом индуктивности.