Магнитоемкостные эффекты в твердых растворах Yb xMn 1-xS

Введение. Материалы на основе твердых растворов Yb x Mn 1-x S в перспективе могут использоваться в качестве сенсоров, датчиков, устройств записи-считывания информации. Изменение диэлектрической проницаемости в магнитном поле может найти применение при изготовлении СВЧ-приборов [1].

Взаимосвязь магнитных и электрических свойств является важным фактором для создания электронных устройств, действующих на новых принципах и открывающих новые направления, такие как спинтроника [2] и новые материалы-мультиферроики [3]. Для мультиферроиков характерно наличие магнитного и ферроэлектрического упорядочения [4]. Существуют два основных микроскопических механизма магнитоэлектрического эффекта – это спин-орбитальный механизм [5] и зависимость обменных взаимодействий от координат магнитных ионов [6] и их изменение в магнитном поле [7; 8]. На границе раздела магнитной и диэлектрической среды нарушается симметрия относительно инверсии пространства и времени и создаются условия для создания магнитоэлектрического эффекта. При наличии электрической неоднородности возможен магнитоемкостный эффект в отсутствие магнитного порядка [9], например, диэлектрический резонанс зависит от магнитного поля в результате изменения подвижности носителей тока в магнитном поле [10; 11].

Цель данной работы – выяснить механизм магнитоэлектрической связи в области комнатной температуры в отсутствие спинового порядка, определить оптимальные условия возникновения магнитоемкостного эффекта по температуре и по концентрации.

Для решения данных задач были проведены измерения диэлектрической проницаемости и тангенса угла потерь для ряда частот в отсутствие магнитного поля и в магнитном поле, индуктивности и добротности магнитных колебаний.

Под магнитоэлектрическим эффектом понимают эффект возникновения намагниченности под действием электрического поля и электрической поляризации под действием магнитного поля: M = α E ; P = α H , где M – намагниченность; E – электрическое поле; P – поляризация, H – магнитное поле; α – магнитоэлектрический коэффициент.

Под гигантской магнитоемкостью понимается относительное изменение диэлектрической проницаемости в магнитном поле: MC ( H ) = (ε ( H ) – ε (0)) / ε (0), где ε ( H ) – диэлектрическая проницаемость материала в магнитном поле H ; ε (0) – диэлектрическая проницаемость в отсутствие поля. Магнитоемкость МС принято измерять в процентах [3].

Линейный магнитоэлектрический эффект [12] может возникнуть в результате зависимости орбитальных магнитных моментов от полярных искажений, индуцированных под действием электрического поля, так называемый ионно-орбитальный вклад в магнитоэлектрический отклик. Средний орбитально-индуци- рованный магнитный момент в электрическом поле, приложенном по оси, имеет намагниченность вдоль оси. Орбитальное упорядочение наблюдалось в оксидах железа [13] и манганитах [14; 15].

На основе симметрийного анализа и новой методики расчета определен спиновый и орбитальный вклад в магнитоэлектрический эффект [12] для LiFePO 4 , который может быть сопоставим по величине со спиновым вкладом либо релятивистским, либо обменно-стрикционного происхождения в 3d-соединениях переходных металлов. Температурная зависимость магнитоэлектрического эффекта, вызванного орбитальным магнетизмом [16], совпадает с параметром порядка и с температурной зависимостью магнитострикции, что приводит к качественному согласию с экспериментальными данными для различных коллинеарных антиферромагнетиков, таких как Cr 2 O 3 , LiCoPO 4 , TbPO 4 .

Если симметрия допускает связь между орбитальным магнитным моментом и полярным искажением, то величина магнитоэлектрического эффекта зависит не только от спин-орбитального взаимодействия, но и от величины щели между основным и возбужденным состояниями, для которых < ψ 0 | L ^μ | ψ n > ≠ 0, а также от зависимости энергии ионных орбиталей от полярных искажений кристаллического поля. Большой магнитоэлектрический эффект, индуцированный орбитальным моментом, возможен в соединениях с анизотропным g -фактором и анизотропией магнитной восприимчивости в парамагнитном соединении, например, в веществах с низкой симметрией координации полярного кислорода, содержащих магнитные ионы с большим спин-орбитальным взаимодействием [12; 17].

В электрических неоднородных системах эффект Максвелла–Вагнера [10] и контактные эффекты могут привести к гигантским значениям диэлектрической проницаемости и диэлектрической релаксации в отсутствие дипольной релаксации [18]. Эффект Максвелла–Вагнера также может индуцировать магнитоемкость в отсутствие взаимодействия между магнитной и электрической подсистемами, при условии существования магнитосопротивления в материале [9]. Такие эффекты ясно демонстрируют, что наличие магнитоемкости не достаточно для отнесения этих соединений к мультиферроикам. С другой стороны, магнитоемкость без магнитоэлектрической связи может быть более практичной для технологических применений, так как не требуется существование дальнего магнитного порядка.

В работе [9] исследована двумерная (2D) композитная среда, описывающая характерные черты неупорядоченного материала, в предположении, что масштаб длины неоднородностей значительно больше, чем у всех масштабов длин микроскопических систем, например, длина свободного пробега электрона. Локальная плотность тока j (ω, r ) связана с локальным электрическим полем E (ω, r ) законом Ома:

j (ω, r ) = σ (ω, r ) E (ω, r ) ≡ i ωε (ω, r ) E (ω, r ), где σ (ω, r ) является локальным тензором проводимости и ε (ω, r ) – локальная диэлектрическая функция. Модель справедлива при двух условиях: 1 / ω много больше времени рассеяния и собственная проводимость и диэлектрическая проницаемость каждой компоненты не зависят от частоты.

При низких частотах ωτ < 1 доминирует емкостное сопротивление, в то время как на высоких частотах ωτ > 1 напряжение в основном падает на резисторе, так как не хватает времени для зарядки конденсатора. Таким образом, при характерной частоте ωτ = 1 быстрое изменение действительной части диэлектрической проницаемости Re [ε xx (ω)] связано с пиком в мнимой части диэлектрической проницаемости Im [ε_xx(ω)], что иллюстрирует проявление эффекта Максвелла–Вагнера в неоднороднодной смеси [11]. Неоднородность играет аналогичную роль в dc -магнитотранспортных свойствах в неупорядоченных средах, так как здесь смешивается холловское сопротивление с продольными компонентами проводимости, что приводит к линейной зависимости магнитосопротивления от магнитного поля [11].

Холловская компонента ε xx (ω) эквивалентна продольному диэлектрическому отклику из однородного материала в отсутствие магнитного поля с диэлектрической проницаемостью ε и сопротивлением β p , которое является сопротивлением Холла для dc -магнитотранспорта. Продольный диэлектрический отклик ε xx (ω) состоит из смеси диэлектрических и резистивных компонент как в действительной, так и в мнимой частях.

Для больших магнитных полей β > 1 или для малых частот ωτ < 1 наблюдается диэлектрический резонанс при βωτ = 1, где Im [ε xx (ω)] обладает ярко выраженным пиком и Re [ε xx (ω)] резко меняется. Резонансная частота определяется холловским сопротивлением β p вместо концентрации р, как в обычном эффекте Максвелла–Вагнера. Положение пика в частотной области обратно пропорционально β. Если βωτ = 1, то высота пика равна Im [ε xx (ω)] ≃ εβ / 2 и растет линейно с полем. Однако величина релаксации в области резонансной частоты остается постоянной, потому что Re [ε_xx(ω)] ≃ 2p и действительная часть Re [ε xx (ω)] становится отрицательной для βωτ ≥ 1 и β > 1, но она обладает обычной диэлектрической релаксацией Максвелла–Вагнера в нулевом магнитном поле. Однако модель не работает и дает отсутствие релаксации, т. е. пик в Im [ε xx (ω)] отсутствует в нулевом магнитном поле β = 0 для всех концентраций. Хотя в простейших композитах из металла и диэлектрика наблюдается пик диэлектрической релаксации. Предполагается, что введение анизотропии может восстановить пик релаксации [19]. Зависимость диэлектрического резонанса от магнитного поля уже наблюдалась экспериментально в нанопористом кремнии [20], который можно представить в виде композита «проводник–диэлектрик».

В принципе, диэлектрический резонанс можно использовать в качестве магнитного датчика, обладающего повышенной чувствительностью к полям в окрестностях β ~ 1 / ωτ. Поэтому задача состоит в том, чтобы сделать его эксплуатацию в диапазоне частот

ω = 1 кГц – 1 МГц при комнатной температуре и для H < 1 Tл. Этим требованиям удовлетворяют полупроводники с большой шириной запрещенной зоны Δ > 0,5 эВ и высокой подвижностью μ > 1 T ^–1 . В работе [9] продемонстрирована возможность существования магнитоемкости в области комнатных температур в немагнитных материалах с неоднородным распределением плотности электрического заряда. В рамках простой двумерной, двухкомпонентной композитной среды вычислили характерный диэлектрический резонанс, который зависит от магнитного поля.

Экспериментальные результаты. Диэлектрические свойства твердых растворов Yb_хMn_1-хS исследовались на основе измерений действительной и мнимой частей диэлектрической проницаемости в области температур 80 К <  T < 400 К без поля и в магнитном поле Н = 0,8 Тл для составов с х = 0,05 и x = 0,1.

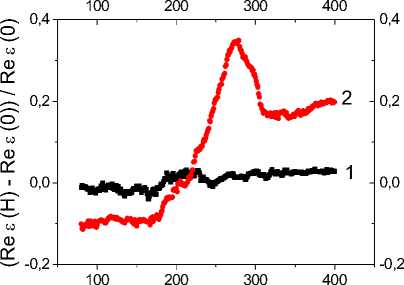
Действительная и мнимая части диэлектрической проницаемости измерены в области температур 80 К <  T < 400 К на четырех частотах: ω = 1, 10, 66 и 100 кГц, в отсутствие магнитного поля и в магнитном поле Н = 0,8 Тл. На рис. 1 изображены температурные зависимости диэлектрической проницаемости, измеренные на частоте ω = 10 и 100 кГц для состава с x = 0,05. С ростом температуры диэлектрическая проницаемость растет и имеет точку перегиба в интервале 180–190 К, причем соответствующая температура сдвигается в область высоких температур c ростом частоты. Диэлектрическая проницаемость имеет широкий максимум при Т = 280 К на частоте ω = 100 кГц, и величина магнитоемкостного эффекта составляет 35 % в окрестности этой температуры. Относительное изменение диэлектрической проницаемости в магнитном поле представлено на рис. 1, a . В области низких температур магнитоемкость отрицательна и наблюдается смена знака с отрицательного на положительный при Т = 182 К и Т = 204 К соответственно для частот ω = 10 и 100 кГц. В области комнатной температуры магнитоемкость увеличивается на порядок при изменении частоты с ω = 10 до 100 кГц.

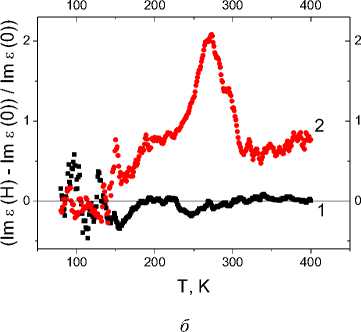
Мнимая часть диэлектрической проницаемости резко увеличивается в интервале температур 155 К <  T < 190 К и при дальнейшем нагревании практически не зависит от температуры на частоте ω = 10 кГц и имеет максимум в Im (ε) при Т = 250 К, который сдвигается до Т = 270 К в магнитном поле (рис. 2). В магнитном поле динамическая проводимость уменьшается в интервале 105 К <  T < 180 К и в интервале 230 К <  T < 300 К и увеличивается при T > 137 К соответственно на частотах ω = 10 и 100 кГц для состава с x = 0,05 [21].

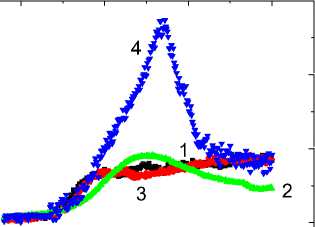
В твердом растворе Yb 0,1 Mn 0,9 S температуры максимумов d Re (ε) / dT совпадают с максимумами мнимой части диэлектрической проницаемости (рис. 3), с ростом частоты для ω = 1, 10 и 100 кГц сдвигаются в область высоких температур при Т = 126, 147 и 172 К и описываются в модели дебаевской релаксации дипольного момента. В области комнатных температур Т = 275–283 К наблюдается острый максимум в Re (ε ( T )) (рис. 3). Величина диэлектрической проницаемости уменьшается с ростом частоты по степенному закону: Re (ε (ω)) ~ 1 / ω ⁿ , однако в магнитом поле Re (ε (ω)) растет с увеличением частоты при Т < 150 К, что характерно для неупорядоченных систем, например в дипольных стеклах.

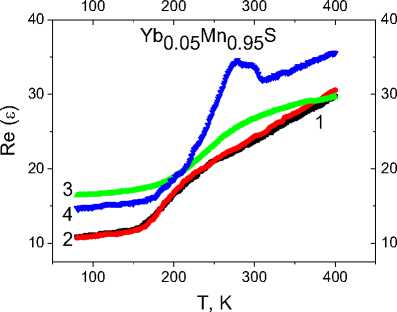
Рис. 1. Температурная зависимость действительной части диэлектрической проницаемости для образца Yb_xMn_1-xS c x = 0,05 без поля на частотах 10 кГц (1), 100 кГц (3) и в магнитном поле H = 0,8 Тл на частотах 10 кГц (2), 100 кГц (4) ( a ); относительное изменение действительной части диэлектрической проницаемости в магнитном поле H = 0,8 Тл на частотах 10 кГц (1) и 100 кГц (2) ( б )

T, K

б

Е 4

200        300

T, K

а

Re ( ε )

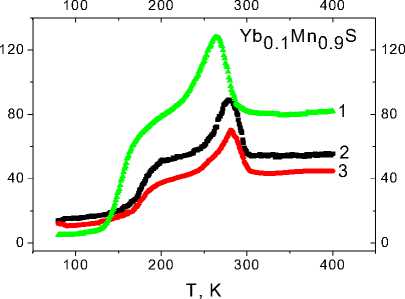
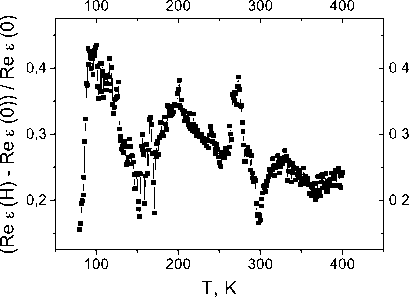
Рис. 3. Температурная зависимость Re (ε) для образца Yb_xMn_1-xS c x = 0,1 без поля на частоте 100 кГц (2) и в магнитном поле H = 0,8 Тл на частотах 10 кГц (1), 100 кГц (3) ( a ); относительное изменение Re (ε) в магнитном поле H = 0,8 Tл на частоте 100 кГц ( б )

Рис. 2. Температурная зависимость мнимой части диэлектрической проницаемости для образца Yb_xMn_1-xS c x = 0,05 без поля на частотах 10 кГц (1), 100 кГц (2) и в магнитном поле H = 0,8 Тл на частотах 10 кГц (3), 100 кГц (4) ( a ); относительное изменение мнимой части диэлектрической проницаемости в магнитном поле H = 0,8 Тл на частотах 10 кГц (1) и 100 кГц (2) ( б )

б

100       200       300       400

100       200       300       400

T, K

а

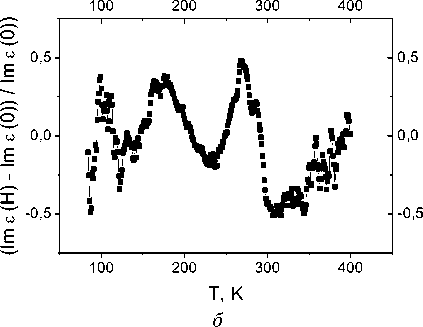
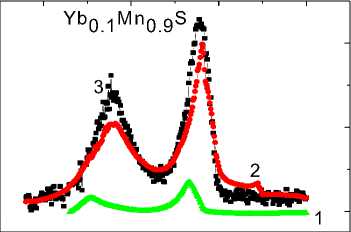
Рис. 4. Температурная зависимость Im (ε) для образца Yb x Mn 1-x S c x = 0,1 без поля на частоте 100 кГц (2) и в магнитном поле H = 0,8 Тл на частотах 10 кГц (1), 100 кГц (3) ( a ); относительное изменение Im (ε) от температуры в магнитном поле Н = 0,8 Тл на частоте 100 кГц ( б )

Магнитоемкость, определенная как δ (ε) = (ε ( Н ) – – ε (0)) / ε (0), резко возрастает при переходе в магнитоупорядоченное состояние при Т <  T N , проходит через максимум и асимптотически исчезает при Т = 75 К. Возможный механизм связан с магнитоупругим взаимодействием. По сравнению с x = 0,05 наблюдается дополнительный максимум в δ (ε) при Т = 200 К и аналогичный максимум при Т = 277 К, который сопровождается максимумом диэлектрических потерь и максимумом в оптической проводимости, изображенной на рис. 4. В области комнатных температур и выше магнитоемкость составляет ~ 25 % [21; 22].

Магнитная проницаемость твердых растворов Yb x Mn 1-x S определялась из индуктивности соленоида с внутренним диаметром d = 2 мм и длиной 10 мм, внутрь которого помещался образец. Измерялась индуктивность катушки с образцом ( L f ) и без образца ( L_s ), так как индуктивность соленоида пропорциональна L = n ² μμ 0 V , то магнитную проницаемость μ r образца с объемом V f найдем как μ r = ( L f – L s ) / L s + 1 [23].

Проницаемость μ r измерялась при охлаждении образцов в нулевом магнитном поле и в поле 0,5 Тл. Для состава с х = 0,1 ниже Т = 190 К наблюдается различие (μ r ^ZF – μ r ^FC ) и минимум на температурной зависимости магнитной проницаемости при Т = 295 К с дальнейшим монотонным ее увеличением.

При переходе в магнитоупорядоченное состояние температура максимума магнитной проницаемости сильно зависит от частоты и смещается в сторону высоких температур от Т = 112 К (ω = 0,1 кГц), Т = 136 К (ω = 1 кГц) к Т = 169 К (ω = 10 кГц) на частотах меньше и включая 10 кГц (рис. 5) и на частоте 10 кГц имеет максимум в окрестности температуры Нееля.

Добротность колебаний монотонно уменьшается при нагревании, как видно на рис. 6, и проходит через максимум на частоте 10 кГц и через минимум – на частоте 50 кГц. В магнитоупорядоченной фазе добротность колебаний и время релаксации колебаний намагниченности обнаруживают зависимость от пре- дыстории образца. Время релаксации τ = Q / π зависит от температуры по степенному закону в парамагнитной области. Относительное изменение добротности магнитных колебаний наглядно показано на рис. 7. Наблюдаемые аномалии динамических характеристик объясняются орбитальным магнитным моментом электронов.

Модель и обсуждение результатов. Из экспериментальных результатов по диэлектрическим, электрическим и магнитным свойствам можно выделить три интервала температур: два низкотемпературных – Т = 160–180 К, 260–290 К и высокотемпературный – 470–490 К. Низкотемпературная аномалия связана с конденсацией ян-теллеровской моды. В результате химического давления происходит перераспределение электронной плотности между t _{2 g}- и e_g -состояниями, либо в результате гибридизации 3d- и 5d-волновых функций часть электронов ионов марганца переходят в зонные состояния и образуются дырки в t 2 g - и e g - состояниях Mn ²⁺ , т. е. ион марганца становится ян-теллеровским ионом, и при понижении температуры понижается кубическая симметрия ионов марганца, например, за счет смещения иона из центра октаэдра с образованием квазивырожденных состояний по кубическим осям кристалла. Можно предположить, что в интервале 160–180 К образуется дипольное стекло, для которого характерно смещение максимума мнимой части диэлектрической проницаемости в область высоких температур с ростом частоты. При нагревании выше 160 К в окрестности температуры замерзания диполей диэлектрическая проницаемость растет. В этой области температур также меняется объем решетки, найденный из коэффициента теплового расширения, и наблюдается небольшой скачок в магнитной восприимчивости в результате уменьшения косвенного обменного взаимодействия через анион серы, так как J = 2 ( t + δ) ( t – δ) / ( E Mn – E s + U ), где δ – смещение иона из центросимметричного положения иона [24].

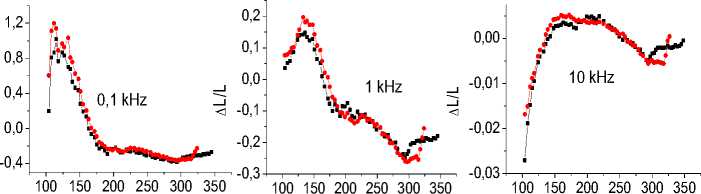
T (K)                              T (K)                                T (K)

а                             б                               в

Рис

. 5. Относительное изменение индуктивности образцов, охлажденных в нулевом магнитном поле (квадрат) и в поле (кружок), от температуры для х = 0,1 на частотах 0,1 кГц ( a ); 1 кГц ( б );

10 кГц ( в )

о3

• — ■— Q (100 kHz)

• — •— Q (100 kHz), H

• — X— Q (50 kHz)

Q (50 kHz), H

Q (10 kHz)

Q (10 kHz), H

Q (1 kHz) -•- Q (1 kHz), H

Q (0,1 kHz)

Q (0,1 kHz), H

100    150    200    250    300    350

T (K)

Рис. 6. Добротность магнитных колебаний в образце, охлажденном в магнитном поле и без поля, от температуры для х = 0,1

-0,1

100    150    200    250    300    350

T (K) б

0,04

0,02

0,00

-0,02

100    150    200

в

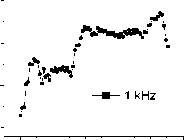
250    300    350  100    150    200    250    300    350

T (K)                                    T (K)

г

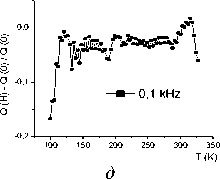
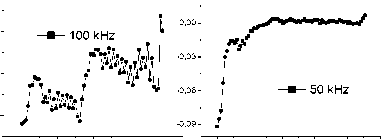
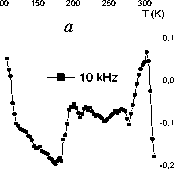
Рис. 7. Относительное изменение добротности магнитных колебаний в образце Yb_xMn_1-xS с x = 0,1, охлажденном в магнитном поле и без поля, от температуры на частотах 100 кГц ( a ); 50 кГц ( б );

10 кГц ( в ); 1 кГц ( г ); 0,1 кГц ( д )

В области температур 260–290 К наблюдается корреляция в изменении температурных зависимостей диэлектрической проницаемости (ε( Т ) имеет максимум), минимум в коэффициенте теплового расширения от температуры и отклонение магнитной восприимчивости от закона Кюри–Вейсса. Возможно, это обусловлено поворотом октаэдра, содержащего внутри ион иттербия, и концентрация таких кластеров максимальна при x = 0,08 и резко падает с ростом концентрации иттербия. Полярные смещения ионов серы вызывают рост диэлектрической проницаемости, понижения локального кристаллического поля на ближайших ионах марганца в окрестности редкоземельного иона индуцируют расщепление и сдвиг t 2 g -состояний ионов иттербия и индуцируют орбитальный магнитный момент, направления которого вырождены вследствие поворота октаэдра вокруг одной из трех осей 4-го порядка. Это вырождение снимается внешним магнитным полем и обусловливает магнитоемкость твердых растворов Yb_xMn_1-xS. Смягчение локальных оптических мод колебаний приведет к максимуму в мнимой части диэлектрической проницаемости из-за фонон-фононного взаимодействия и к максимуму в действительной части диэлектрической проницаемости. При этой температуре к спиновому моменту добавляется орбитальный момент, что приводит к увеличению эффективного момента и к уменьшению величины наклона обратной магнитной восприимчивости.

Одним из механизмов, объединяющих эти эффекты, является уменьшение подвижности электронов и образование фазового расслоения электронов на гра- нице раздела Mn–Yb. Частичная локализация электронов на интерфейсе Mn–Yb является причиной образования объемной неоднородности электрического заряда. В отсутствие магнитного поля электрический заряд распределен в плоскостях xy, zx, zy (рис. 8).

В магнитном поле, направленном перпендикулярно к одной из плоскостей, происходит перераспределение заряда, и заряд двигается в плоскости перпендикулярно полю на границе раздела Mn–Yb, что схематично представлено на рис. 8. Это эквивалентно представлению о двух параллельно соединенных конденсаторах без поля, а в поле сохраняется заряд на одном из конденсаторов, и, соответственно, емкость увеличивается в два раза.

Заключение. Для твердых растворов Yb x Mn 1-x S с x = 0,05 и x = 0,1 найдено смещение максимума диэлектрических потерь в сторону высоких температур в интервале 160 К <  T < 200 К с ростом частоты и рост диэлектрической проницаемости от частоты ниже 160 К, что характерно для дипольного стекла.

Обнаружены магнитоемкостные эффекты для Yb x Mn 1-x S с х = 0,05 и x = 0,1 при температурах выше комнатной, причем для х = 0,05 магнитоемкость меняет знак в окрестности 200 К.

При переходе в магнитоупорядоченное состояние температура максимума магнитной проницаемости сильно зависит от частоты и смещается в сторону высоких температур и на частоте 10 кГц имеет максимум в окрестности температуры Нееля. Добротность колебаний монотонно уменьшается при нагревании. Время релаксации зависит от температуры по степенному закону в парамагнитной области.

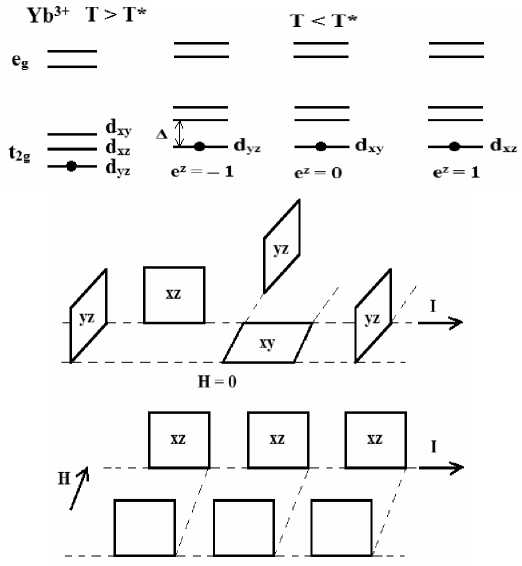
Рис. 8. Снятие вырождения электронной структуры ионов Yb

Магнитоемкостные эффекты объясняются в модели орбитального упорядочения электронов. Смена знака магнитоемкости по температуре объясняется образованием магнитного и орбитального упорядочения при разных температурах.