Магнитогидродинамические перемешиватели жидких металлов с несинусоидальными токами

В процессе приготовления металлических сплавов, в частности на основе алюминия, перемешивание многокомпонентного расплава в ванне печи-миксера позволяет выровнять химический состав и температуру расплава во всем объеме ванны и тем самым повысить производительность печи-миксера и снизить энергопотребление на единицу продукции [1].

В настоящее время широкое распространение получили индукционные магнитогидродинамические (МГД) перемешиватели, позволяющие бесконтактно воздействовать на расплав и полностью автоматизировать этот процесс.

Используемые МГД-перемешиватели, как правило, питаются синусоидальными токами, имеют низкую эффективность и коэффициент мощности. Особенно низкая эффективность проявляется при устранении неоднородностей многокомпонентных расплавов на молекулярном уровне.

Целью работы стало исследование вопроса повышения эффективности и снижения потребления реактивной мощности МГД-перемешивателей путем использования несинусоидального периодического питания. Показано, что при определенных параметрах индуктора и режимах

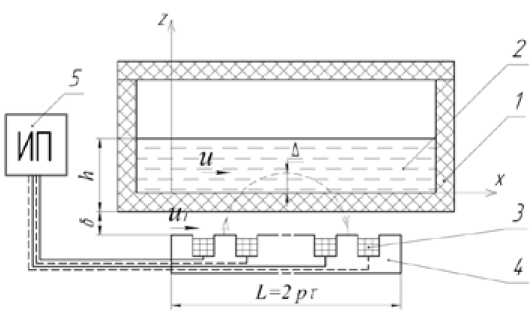
По принципу действия индукционные МГД-перемешиватели аналогичны линейным индукционным машинам [2]. На рисунке 1 представлен эскиз печи-миксера с МГД-перемешивателем, установленным под подиной ванны [3]: 1 – ванна печи-миксера; 2 – жидкий металл (расплав); 3 – многофазная обмотка индуктора; 4 – сердечник индуктора; 5 – источник питания.

Индуктор МГД-перемешивателя состоит из многофазной обмотки 3 и сердечника 4. Длина сердечника L = 2pτ , где p – число пар полюсов; τ – полюсное деление.

При подключении многофазной ( m = 2, 3 - число фаз) обмотки к источнику периодического синусоидального или несинусоидального напряжения в зазоре между индуктором и расплавом образуется бегущее магнитное поле. Скорость движения амплитуды магнитной индукции в направлении оси X равна u 1 = 2Tf, где f - частота тока. При взаимодействии бегущего магнитного поля с наведенными в расплаве электрическими токами расплав начинает двигаться со скоростью u также в направлении оси x, осуществляя перемешивание расплава в ванне.

Эффективность перемешивания зависит от глубины проникновения электромагнитного поля в расплав. Синусоидальное электромагнитное поле по мере распространения в расплав (ось Z ) затухает по экспоненциальному закону [2]. Так, зависимость комплексной величины магнитной индукции от координаты ( Z ) описывается выражением

B ( z ) = B _Q.e - , (1) где B 0 - величина магнитной индукции на поверхности расплава (T).

Комплексное значение ф равно

п г ф = J—

+ i ®M ₀ y ,                                                          (2)

где τ – полюсное деление индуктора ( m) ; ω = 2πf – угловая частота ( rad/s ); f – частота тока ( 1/s ); μ 0 = 4π∙10^-7 – магнитная постоянная ( H/m ); γ – удельная электропроводность расплава ( 1/Ω∙m ); i = v-l ^- мнимая единица.

Расстояние, на котором электромагнитное поле уменьшается в e~2,72 раза ( e - основание натурального логарифма), называется глубиной проникновения электромагнитного поля. В соответствии с (1-2) глубина проникновения электромагнитного поля А обратно пропорциональна φ и при неизменных свойствах расплава зависит от частоты тока f и полюсного деления индуктора т . При т^да глубина проникновения электромагнитного поля равна глубине проникновения плоской электромагнитной волны и при неизменных свойствах расплава полностью зависит от частоты тока f [4]:

А = —. (3) V ®И о 7

В реальных индукторах величина полюсного деления τ имеет ограниченное значение и обычно выбирается из условия т~(3-5)о, где о - величина расстояния от магнитопровода индуктора до расплавленного металла. Чем меньше τ, тем быстрее затухает электромагнитное поле в расплаве. При фиксированном τ глубина проникновения электромагнитного поля также зависит от частоты тока f . Если f = 0 (постоянный ток в обмотке индуктора), то в соответствии с (2) глубина проникновения магнитного поля (также постоянного во времени) будет максимальной и равной

А = Т. (4) п

Постоянное магнитное поле не взаимодействует с расплавом. Наведенные в расплаве токи, соответственно, и электромагнитные силы, действующие на расплав, пропорциональны скорости изменения магнитного поля. Следовательно, для увеличения электромагнитных сил, перемешивающих расплав, необходимо увеличивать частоту f , но при этом уменьшается глубина проникновения электромагнитного поля в расплав и эффективность перемешивания снижается.

Известно, что источниками электромагнитного поля индуктора являются электрические токи в обмотке индуктора. В связи с этим целесообразно сравнить электромагнитные характеристика двух МГД-перемешивателей. Первый питается синусоидальными периодическими токами, второй - несинусоидальными, которые в течение полупериода Т/2 имеют один интервал времени, когда di/dt+О , а в течение другого интервала времени di/dt = 0 .

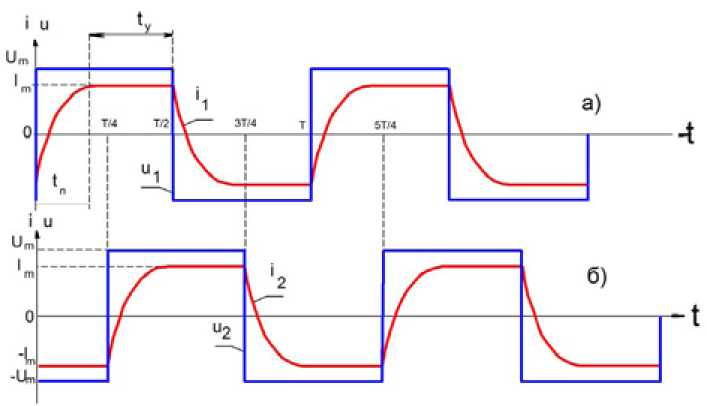
При рассмотрении второго варианта предположим, что на каждую фазу обмотки индуктора подается периодическое напряжение прямоугольной формы u(t) (рис. 2). Поскольку каждая фаза имеет активное сопротивления R и индуктивность L, в ней возникает переходный процесс при каждом изменении полярности напряжения. Длительность переходных процессов tп зависит от параметров индуктора R и L, а именно определяется постоянной времени тв и приблизительно равна tп ≈ 3τв , (5)

где τ в ≈L/R [5] .

С учетом законов коммутации и характера протекания переходных процессов форма электрического тока i(t) будет иметь вид, также представленный на рис. 2.

По окончании переходного процесса в обмотке возникает установившееся состояние длительностью tу, в течение которого ток не меняется, и его величина определяется выражением iy =± Um" .                                                              (6)

R

Электромагнитное поле будет повторять форму токов. Условно процесс взаимодействия такой формы поля с жидким металлом ванны можно разделить на два. Первый – когда поле не меняется (время t_у ) и проникает в толщу металла максимально глубоко, и второй – когда поле меняется во времени с большой скоростью (время t п ) и в толще металла 5 наводятся кольцевые (вихревые) токи, которые, взаимодействуя с полем, создают силу, приводящую металл 5 в движение. Для эффективного перемешивания жидкого металла в ванне целесообразно на расплав воздействовать бегущим электромагнитным полем. Для этого в индукторе устанавливают две и более обмотки, которые запитываются от источника одинаковым по форме и частоте напряжением, но при этом напряжения сдвинуты по фазе. Например, для двухфазного индуктора ( m = 2 ) фазовый сдвиг между напряжениями может быть T/4 (рис. 2).

В полученных выражениях для упрощения взаимная индуктивность между обмотками не учитывалась.

В трехфазном индукторе ( m = 3 ) фазовый сдвиг между питающими напряжениями может составлять T/3 .

Так как длительность переходного процесса tn~3L/R, а длительность установившегося состояния ty = T/2 - 3 L,                                                         (7)

R

можно получить различные значения t_y путем изменения параметров индуктора L и R при постоянном значении периода Т

Далее определим электромагнитные характеристика МГД-перемешивателей с синусоидальным и несинусоидальным периодическим питанием при различных значениях относительного параметра t_y* = t_y/(0,5T).

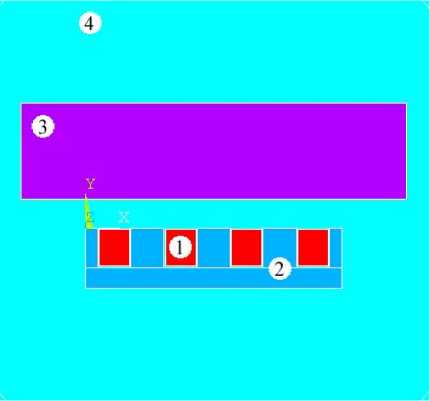
На рис. 3 представлена расчетная 2D-модель системы «индуктор – расплав», построенная в расчетном комплексе ANSYS. Для построения модели были выделены следующие подобласти: 1, 2 - индуктор; 3 - расплав; 4 - окружающее пространство. Подобластям были присвоены следующие материалы с соответствующими электрофизическими свойствами: 1 – медь ( ρ = 1,7e-8 Ω∙m, μ r = 1 ); 2 – шихтованная трансформаторная сталь ( ρ x = 14e-8 Ω∙m, ρ y = 14e-8 Ω∙m, ρ z = 1e32 Qm, ^ r = 300 ); 3 - алюминий при t = 730 °C ( р = 24,76e-8 Q^m, ^ r = 1 ).

При постановке задачи приняты следующие допущения:

• 1.    Магнитная проницаемость магнитопровода имеет постоянное значение.

• 2.    Расчет электромагнитного поля проводится без учета поля скоростей.

• 3.    В качестве источника задается источник тока, имеющий линейные переходы.

Система уравнений, описывающих электромагнитное поле, состоит из уравнения на векторный магнитный потенциал и уравнения непрерывности. С учетом принятых допущений эта система имеет вид:

∇ ² A =- µ _a δ ,                                                        (8)

V S = 0 ,                                                                     (9)

где A – магнитный потенциал, ( V∙s/m ); μ_a – абсолютная магнитная проницаемость; δ – вектор плотности электрического тока, ( A/m² ):

∂ Α δ = - γ   .

∂ t

Чтобы электромагнитное поле в расчетной области определялось однозначно, дополним систему уравнений (8 – 9) граничными условиями. Считая, что расчетную область окружает среда с идеальными магнитными свойствами ( ц = «), на границах расчетной области для касательной и нормальной составляющих векторного магнитного потенциала будут выполняться условия:

А = о d n

A n = 0 ,                                                                        (12)

где A и A – тангенсальная и нормальная составляющие векторного магнитного потенциала; τn n – нормаль к поверхности.

В качестве источникового члена задавался источник тока. Функция двух фаз синусои дального периодического тока имеет вид:

i 1 ⁽ t ) = I m sinC M t ) , i 2 ⁽ t ) = I m Sin. ²^ + П / 2) ,

несинусоидального периодического тока:

T m

t

i 1 ( t ) =

I

( t - t п

Im

-

tу

-

I m

^, _t <  t <  t t + ₁ , п    пу

• ¹    I, п у              п у

• ²    j , ² t п ⁺ t у < t <  ² t п ^{+ 2} t у

I

m

^ t у t у

i 2 ⁽ t ) = 4

/

I ^m

11

² J

I ^m

t

t ^п

t у

tп

I m

T /4 <  t <  T /4 + 1 , п

^{, T +} t ^п < t <^{T +} t ^{п +} t ^у

¹ ] ' t^t, /⁴₊⁺ + t ^п + < <  t /4 + 2 1 • +, ^{2 J} , / t ^п t ^у t / t ^п t ^у .

Для проверки построенной математической модели была разработана и собрана экспериментальная установка (рис. 4) 2-фазного индуктора 1 с импульсным источником питания 2. Частота питания индуктора 3±0,3 Hz током 20 А .

Измерение электромагнитного поля проводили с помощью двух датчиков Холла, расположенных ортогонально друг к другу. Такие датчики дают две пространственные компоненты вектора напряженности магнитного поля. Результаты измерений выводили на дисплей осциллографа 3 и в текстовый файл. Воздействие периодическим несинусоидальным электромагнитным полем осуществлялось на алюминиевую заготовку 4.

Рис. 4

Датчик для выполнения измерений помещали между центральным зубцом магнитопровода (рис. 4 и 5, точка A) и алюминиевой заготовкой и в той же плоскости в толщине заготовки (рис. 4 и 5, точка B).

С аналогичными параметрами было выполнено численное моделирование с использованием разработанной математической модели [6], в результате которого была получена динамика электромагнитного поля. Так же из точки в расчетной области между центральным зубцом магнитопровода и заготовкой и из точки в толщине заготовки были выведены в текстовый файл две пространственные компоненты вектора напряженности магнитного поля.

График-сравнение полученных данных представлен на рис. 5. Некоторые расхождения результатов математического моделирования и физического эксперимента объясняются тем, что, во-первых, при расчете использовалась 2D-модель, во-вторых, при проведении эксперимента частота прямоугольного периодического напряжения отличалась от расчетной из-за специфики источника питания. Вместе с тем из приведенных графиков видно, что математическая модель правильно воспроизводит характер формы магнитного поля и может быть использована для анализа электромагнитных процессов в МГД-перемешивателях с несинусоидальными периодическими токами.

В ходе численного эксперимента определены дифференциальные и интегральные электромагнитные характеристики системы «индуктор – расплав».

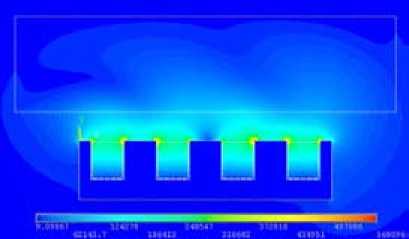
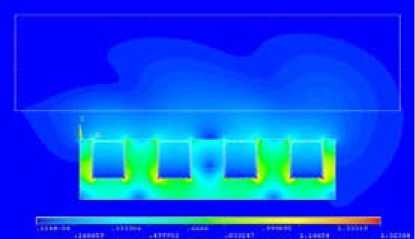
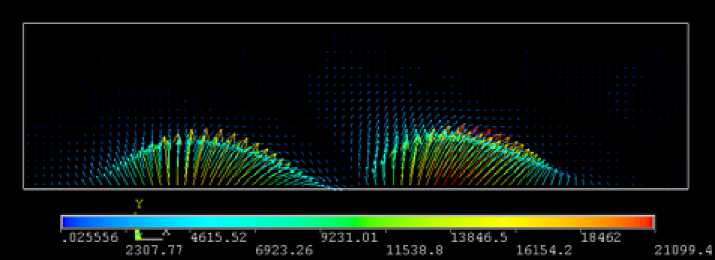
На рис. 6 представлены картины распределения мгновенных значений напряженности магнитного поля H , магнитной индукции B и мгновенных значений объемных электромагнитных сил f в расплаве.

Напряженность магнитного поля H имеет малые значения в магнитопроводе индуктора и достигает большой величины в зазоре и расплаве, магнитная индукция, наоборот, имеет максимальные значения в магнитопроводе и меньшие значения – в зазоре и расплаве. Знание – 172 –

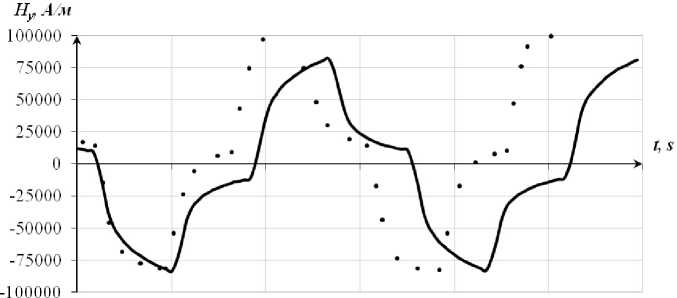
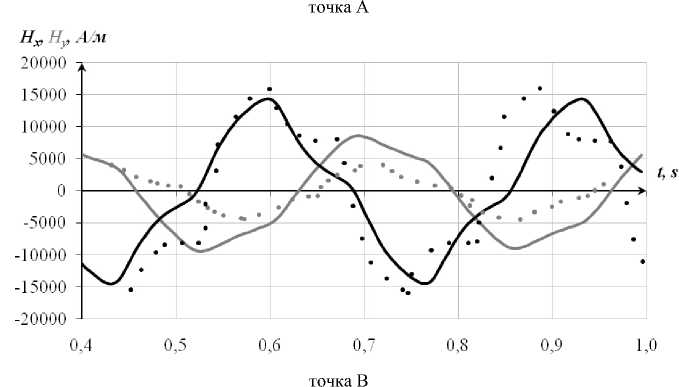
Рис. 5

картин распределения H и B позволяет правильно проектировать магнитопровод и выбрать линейную токовую нагрузку.

Анализ распределения векторов электромагнитных сил, действующих на расплав, позволяет сделать вывод, что нормальные составляющие электромагнитных сил значительно больше касательных. Вместе c тем именно касательные составляющие приводят расплав в движение, совпадающее с направлением бегущего магнитного поля индуктора.

На рис. 7 изображены зависимости относительных составляющих электромагнитной силы F* = e x F* x + e z F* z от относительного параметра 2t_y/T для двухфазной и трехфазной обмоток индуктора соответственно. Здесь F*_x и F*_z – тангенциальная (ось x ) и нормальная (ось z ) составляющие электромагнитной силы соответственно; e x и e z – единичный вектор, направленный по оси x и z соответственно.

За базовые значения средних за период электромагнитных сил приняты тангенциальная F xs и нормальная F zs составляющие электромагнитной силы при питании обмоток синусоидальными токами, т.е.

A

B

Рис. 6

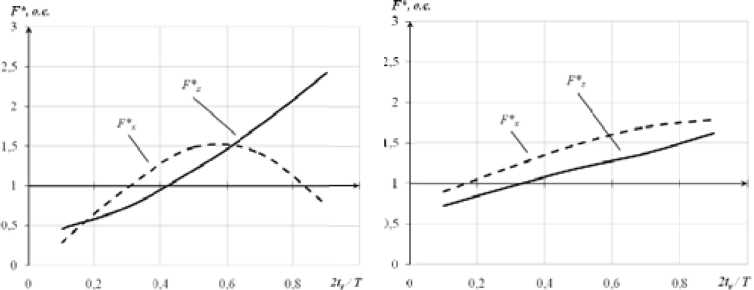
Рис. 7

F *, = ^, F *_z = ^.

^{x    F}xs         ^{z    F}zs

Пунктирные линии на рис. 7 соответствуют тангенциальным, а сплошные – нормальным составляющим электромагнитных сил.

Как следует из приведенных графиков, при tу /0,5T > 0,4

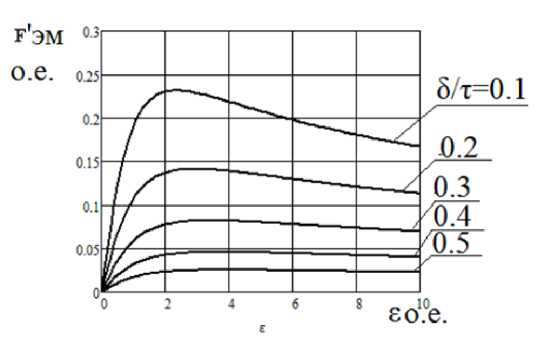
Рис. 8

значения как тангенциальной, так и нормальной составляющих электромагнитной силы при несинусоидальном питании обмоток индуктора превосходят аналогичные значения при питании обмоток индуктора синусоидальными токами. Следовательно, если форма питающих обмотку индуктора несинусоидальных токов имеет такое значение длительности установившегося состояния t_y при заданном периоде T, при котором выполняется неравенство (16), перемешивание будет более эффективным по сравнению с вариантом, в котором обмотка индуктора будет питаться синусоидальными токами.

Величину периода T питающего напряжения можно выбрать из следующих соображений. Известно, что зависимость относительной электромагнитной силы от безразмерной величины ε – коэффициента добротности при различных значениях δ/τ имеет вид, представленный на рис. 8. Здесь δ – расстояние от индуктора до расплава металла. Коэффициент добротности определяется как [2]

s = т ².                                                                      (17)

π

При известном значении δ/τ можно определить значение коэффициента добротности е = e m , при котором относительная электромагнитная сила будет иметь максимальное значение F* эм = F* эм max . Здесь F* эм = F эм /F 0 , где за базисную силу принята F 0 = μ 0 2pτ∙a∙A , ( N ), где p – число пар полюсов индуктора; a – ширина индуктора, m ; A – линейная токовая нагрузка, ⁽ A/m ).

Зная ε_m , в соответствии с (17) можно определить период ( T = 1/f ), а именно

2µ0γτ2 εmπ

Следовательно, индукционная установка, обмотка индуктора которой выполнена таким образом, чтобы соблюдалось условие (16), позволяет подобрать частоту многофазного (m = 2, 3) источника несинусоидального периодического напряжения (выражение 18), при которой будет возможно максимально эффективное перемешивание металла.

Следует отметить, что при наличии в электрической цепи с последовательным соединением R и L элементов периодического тока i напряжение на ее зажимах определяется выражением

u = Ri + L . ∂ t

Во время установившегося состояния t у изменение электрического тока отсутствует ( ∂i/∂t = 0 ) и тогда в соответствии с (19) u = Ri .

В этот период реактивная мощность из сети не потребляется, и, как показали расчеты и измерения на физической модели, в целом потребление реактивной мощности уменьшается по сравнению с вариантом, когда обмотка индуктора питается синусоидальным током.

Таким образом, в результате сравнения двух вариантов МГД-перемешивателей вариант МГД-перемешивателя с несинусоидальными периодическими токами при определенных параметрах индуктора и режимах работы осуществляет более эффективное перемешивание жидких металлов, при этом отмечено снижение потребления реактивной мощности (повышение коэффициента мощности) и сокращение времени перемешивания.

• [1]    Тимофеев В.Н., Корчагин А.И., Павлов Е.А., Тимофеев Н.В. // Journal of Siberian Federal University 1 (2011 5) 28–38.

• [2]    Вольдек А.И. Индукционные магнитогидродинамические машины с жидкометаллическим рабочим телом. Л.: Энергия, 1970. С. 272.

• [3]    Тимофеев В.Н., Христинич Р.М., Бояков С.А., Темеров А.А. // Международный журнал для алюминиевой индустрии. 2009. № 1. С. 16–20.

• [4]    Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: учебник для вузов. Т. 2. 4-е изд. СПб.: Питер, 2003. 576 с.

• [5]    Бессонов Л.А. Теоретические основы электротехники: учебник для студентов энергетических и электротехнических вузов. М.: Высшая школа, 1973. С. 752.

• [6]    Pervukhin M.V., Minakov A.V., Sergeev N.V., Khatsayuk M.U. // Mathematic simulation of electromagnetic and thermal-hydrodynamic processes of the system “inductor-ingot” of an electromagnetic mould. 2011. No. 1. P. 79–88.