Магнитоимпеданс в нестехиометричном сульфиде марганца

Разработка электронных устройств, которые смогут функционировать в экстремальных условиях, например в малых космических аппаратах, где температура окружающей среды меняется от 200 до 400 К, является актуальной задачей. Поэтому привлекает внимание спинтроника [1–4]. Управление транспортными характеристиками в полупроводниках под действием внешнего магнитного поля представляет интерес как с фундаментальной, так и с практической точки зрения [5–8]. В электрически неоднородных полупроводниках транспортные характеристики на постоянном и переменном токе могут качественно отличаться [9]. Это связано с радиусом неоднородности и временем релаксации носителей тока, которое определяется взаимодействием с магнитной и упругой подсистемами. Регулировать электрическую неоднородность можно электронным допированием, концентрацией и температурой.

Например, в манганитах при неизовалентном замещении найдены переходы, связанные с орбитальным, зарядовым и магнитным упорядочением [10–13]. В окислах железа Fe 3 O 4 выше температуры Вервея найден электронный нематик с радиусом корреляции 5–8 нм. Переход Вервея связан с конкуренцией зарядового и структурного порядка в результате электрон-фононного взаимодействия [14]. Можно получить зарядовое упорядочение в сульфиде марганца, где носителями тока являются решеточные поляроны за счет нестехиометрии. Сульфид марганца магнитный полупроводник с температурой Нееля 150 К, щель в спектре электронных возбуждений 3 эВ [15; 16]. Вырождение в области зарядового упорядочения снимается магнитным полем, т. е. топология электрически неоднородного состояния меняется в магнитном поле, что приводит к изменению частотной зависимости диэлектрической проницаемости в магнитном поле, и создаются предпосылки для магнитоимпеданса.

Цель работы – установить влияние магнитного поля на сопротивление на переменном токе и компоненты импеданса в нестехиометричном образце Mn 0.9 S.

Материалы и методы

Фазовый состав и кристаллическая структура образца Mn 0.9 S исследовались на рентгеновской установке ДРОН-3 с использованием CuK_α – излучения при комнатной температуре. Согласно рентгеноструктурному анализу синтезированные соединения являются однофазными и имеют кубическую решетку типа NaCl, как в исходном сульфиде марганца [15].

Импеданс, активная и реактивная части импеданса измерены на анализаторе компонентов AM-3028 в частотном интервале ω = 10² – 10⁶ Гц при температурах 77-500 К, амплитуда переменного напряжения составляла 1 В. Для расчета спектров импеданса применялось программное обеспечение ZView (Scribner Associates Inc.).

Результаты и обсуждение

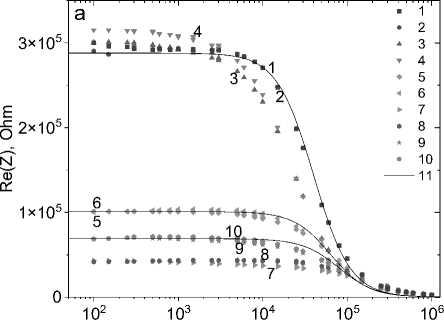
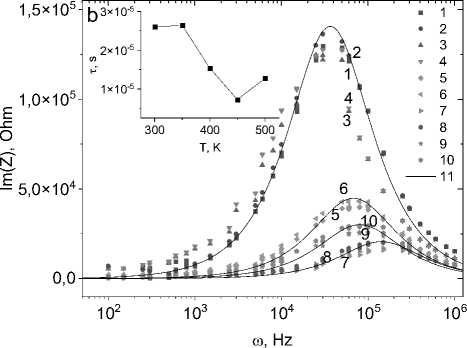
Неоднородное электрическое состояние, образование объемного заряда установим из импедансной спектроскопии [17]. Из импеданса установим динамические характеристики носителей тока, время релаксации, механизм рассеяния носителей тока выявим из импеданса. На рис. 1 представлены частотные зависимости компонент импеданса без поля и в магнитном поле, которые хорошо описываются в модели Дебая [18]:

Re Z ( ю ) =---—г; Im Z ( ю ) = B ®^T , ,

1 + ( ю t ) ²               1 + ( ют ) 2

где τ – время релаксации носителей тока, A и B параметры.

Время релаксации уменьшается при нагревании в пять раз и достигает минимума при 450 К (вставка на рис. 1, b ). При этой температуре проводимость достигает максимума.

ю , Hz

0,1

Ф or <

0,2

0,0

102        103        104        105        106

ю , Hz

ю , Hz

-0,1

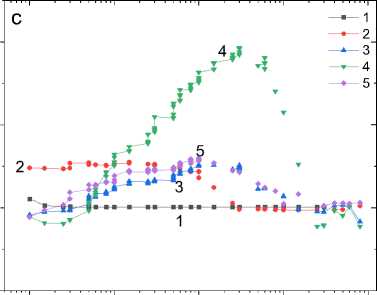
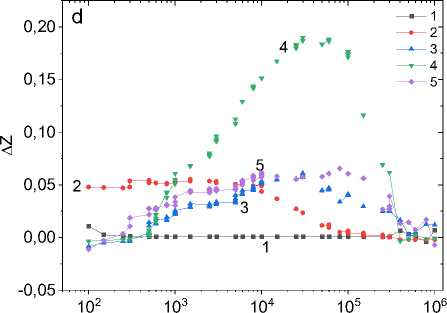
Рис. 1. Частотные зависимости действительной ( a ) и мнимой ( b ) частей импеданса для образца Mn_0.9S без поля H = 0 (1, 3, 5, 7, 9) и в магнитном поле H = 12 кЭ (2, 4, 6, 8, 10) при температурах T = 300 К (1, 2), 350 К (3, 4), 400 К (5, 6), 450 К (7, 8), 500 К (9, 10). Подгоночные функции (11). Вставка: температурная зависимость времени релаксации τ. Частотные зависимости магнитоимпеданса для действительной его части ( c ) и магнитоимпеданса ΔZ ( d ) в магнитном поле H = 12 кЭ при температурах T = 300 К (1), 350 К (2), 400 К (3), 450 К (4), 500 К (5) для образца Mn 0,9 S

Fig. 1. Frequency dependences of the real ( a ) and imaginary ( b ) parts of the impedance for the Mn_0.9S sample without a field H = 0 (1, 3, 5, 7, 9) and in a magnetic field H = 12 kOe (2, 4, 6, 8, 10) at temperatures T = 300 K (1, 2), 350 K (3, 4), 400 K (5, 6), 450 K (7, 8), 500 K (9, 10). Fitting functions (11). Insert: temperature dependence of relaxation time τ. Frequency dependences of the magnetoimpedance for its real part ( c ) and magnetoimpedance ΔZ ( d ) in a magnetic field H = 12 kOe at temperatures T = 300 K (1), 350 K (2), 400 K (3), 450 K (4), 500 K (5) for the Mn 0.9 S sample

Влияние магнитного поля на динамические характеристики носителей тока исследовалось в результате изменения компонент импеданса в магнитном поле при фиксированных температурах:

ΔR = Re(Z(H, ω)) – Re(Z(H = 0, ω)) / Re(Z(H = 0, ω);

ΔZ = (Z(H, ω) – Z(H = 0, ω)) / Z(H = 0, ω))

Импеданс увеличивается в магнитном поле и достигает максимума в области температуры зарядового упорядочения вакансий (рис. 1, d ). Увеличение Re(Z) в магнитном поле вызвано уменьшением диагональной компоненты диэлектрической проницаемости в магнитном поле (рис. 1, с ). Проводимость пропорциональна диэлектрической проницаемости σ = iωε. В электрически неоднородной среде продольная компонента диэлектрической проницаемости имеет вид [19]:

Re [^е хх ( ® ) ] =

е ( 1 -в ² + ( шт )²(1 + в ²)² )

1 + ( ют )²(1 + в ²)²

где β = μН; μ – подвижность; τ = ε/σ.

Наличие объемного заряда, который создается дефектами, можно оценить из годографа импеданса. На рис. 2 изображены годографы импеданса Mn 0,9 S. В модели эквивалентных схем годограф описывается последовательным сопротивлением R 1 и параллельной составляющей R 2 и С (рис. 2). Сопротивление R 1 на порядок меньше R 2 и емкость порядка C ~ 100 пФ.

1,5×105

Е

1,0×105

N е"

5,0×104

0,0

1×105       2×105

Re(Z), Ohm

3×105

Рис. 2. Годографы импеданса для образца Mn 0,9 S в нулевом магнитном поле (1, 3, 5, 7, 9) и в магнитном поле H = 12 кЭ (2, 4, 6, 8, 10) при температурах T = 300 К (1, 2), 350 К (3, 4), 400 К (5, 6), 450 К (7, 8), 500 К (9, 10)

Fig. 2. Impedance hodographs for the Mn 0.9 S sample in a zero magnetic field (1, 3, 5, 7, 9) and in a magnetic field H = 12 kOe (2, 4, 6, 8, 10) at temperatures T = 300 K (1, 2), 350 K (3, 4), 400 K (5, 6), 450 K (7, 8), 500 K (9, 10)

Импеданс определяется активной частью R и реактивной (ωL – 1/ωC) частью. Вклады в импеданс зависят от температуры. Температурная зависимость импеданса Mn0,9S дана на рис. 3. На временах измерений меньше времени релаксации τ < τc до 200 К импеданс обусловлен реактивной частью. Примесные заряженные дефектные состояния экранированы, и емкость практически от температуры не зависит. Деполяризация вызывает незначительный рост сопротивления на постоянном токе и увеличивает вклад в импеданс от реактивной части. При нагревании импеданс уменьшается на 4–5 порядков выше 200 К. Изменение импеданса от температуры имеет активационный характер Z(T) = Z0exp(∆E/kT) c энергией активации ∆E = 0,11 – 0,13 эВ в интервале 250–500 К. Эта энергия соответствует энергии возбуждения решеточных поляронов, которые наблюдались в манганитах La0,9Sr0,1MnO3 и приписываются Ян-Теллеровским поляронам [20–21].

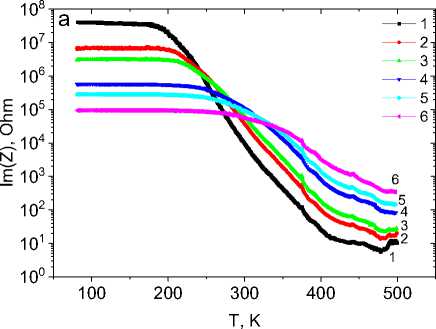
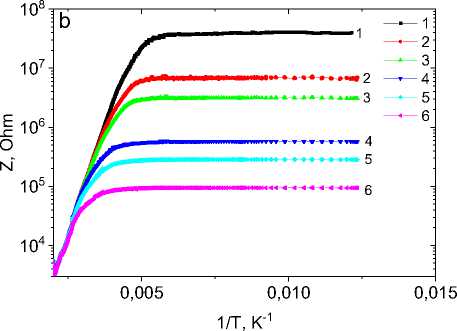
Рис. 3. Температурная зависимость мнимой части импеданса ( a ) и импеданса от обратной температуры ( b ) ω = 1 кГц (1), 5 кГц (2), 10 кГц (3), 50 кГц (4), 100 кГц (5), 1000 кГц (6) для образца Mn 0,9 S

Fig. 3. Temperature dependence of imaginary part of impedance ( a ) and impedance on inverse temperature ( b ) ω = 1 kHz (1), 5 kHz (2), 10 kHz (3), 50 kHz (4), 100 kHz (5), 1000 kHz (6) for the Mn 0,9 S sample

Заключение

Сравнение компонент импеданса в сульфиде марганца с дефектами в катионной системе марганца указывает на основной вклад в магнитоимпеданс электросопротивления. Найдена температура максимума магнитоимпеданса и время релаксации носителей тока. Годограф импеданса описывается одним RC контуром с последовательным сопротивлением и электропроводность определяется объемными свойствами кристаллита. Дефекты в сульфиде марганца Mn 0,9 S обуславливают емкостной вклад в импеданс ниже 200 К. Деполяризация примесных центров при 200 К индуцирует максимум проводимости и переход к активационной зависимости импеданса от температуры, связанной с решеточными поляронами. Найдена температура, при которой минимум релаксации носителей тока вызывает максимум проводимости и увеличение импеданса в магнитном поле.

Acknowledgments. The work was supported by the Russian Medium Fund, the Government of the Krasnoyarsk Territory and the Krasnoyarsk Science Foundation project No. 23-22-10016.