Магнитоимпеданс в тулий марганцевом халькогениде

• 1.    Введение

• 2.    Влияние иона халькогена на частотную зависимость импеданса

Управление транспортными характеристиками в полупроводниках под действием внешнего магнитного поля представляет интерес как с фундаментальной, так и с практической точки зрения [1–4]. В полупроводниках с неоднородным распределением электрического заряда транспортные характеристики зависят от степени неоднородности [5–8]. В спектре электронных возбуждений в запрещенной зоне образуется конечная электронная плотность на уровне химпо-тенциала в результате локализации заряда. При слабом легировании волновая функция электрона остается локализованной. С ростом концентрации замещения в центре зоны формируются делокализованные состояния и при некотором критическом значении возникает бесконечный кластер, при котором волновые функции электрона представляют в виде плоских волн, распространяющихся по всему кристаллу [9; 10].

Регулировать электрическую неоднородность можно за счет флуктуации валентности, концентрации и температуры [11–13]. Например, ион тулия обнаруживает трехвалентное состояние в TmS [14; 15], состояние промежуточной валентности в TmSe [16] и двухвалентное состояние в TmTe [17]. Электронная конфигурация иона Tm2+δ зависит от халькогена. Поэтому замещение иона марганца в халькогенидах MnS и MnSe ионами тулия приведет к разной энергии делокализации электронов. Введение в систему TmSe нестехиометрии способствует увеличению валентности ионов тулия до Tm3+.

Цель работы – выявить влияние ионов халькогена на время релаксации носителей тока, импедансные характеристики и их изменение в магнитном поле.

Твердые растворы Tm x Mn 1–x S синтезировали флюсовым методом из поликристаллического сульфида марганца и моносульфида тулия [18]. Образцы (MnSe) 1-x (Tm 0,76 Se) x получены методом твердофазной реакции в вакуумированных кварцевых ампулах в однозонной печи сопротивления. Подробно методика синтеза описана в [19]. Рентгеноструктурное исследование халькогенидов дает рентгенограмму, соответствующую ГЦК-решетке типа NaCl.

Импеданс, компоненты импеданса реагируют на изменение электронной структуры и локальной деформации решетки, которые меняют функцию распределения электронной плотности. Определение времени релаксации носителей тока является важной характеристикой определения механизма диссипации носителей тока. Релаксация может иметь как активационный, так и безактивационный тип [20].

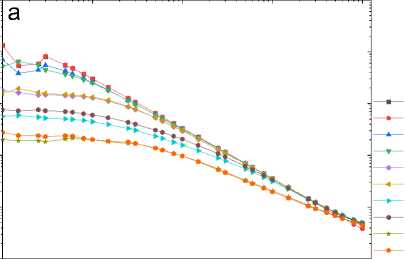
Релаксация носителей тока на частотах выше 1 кГц проявляется при температурах выше комнатной, поэтому зависимость импеданса от частоты без поля и в магнитом поле измерим при температурах выше комнатной. На рис. 1 приведены частотные зависимости импеданса Z(ω) и Im(Z(ω)) для Tm0,05Mn0,95S и (MnSe)1–x(Tm0,76Se)x. При замещении марганца ионами тулия частоты максимумов Im(Z(ω)) смещаются в сторону высоких частот в селениде марганца на два порядка. Независимо от иона халькогена время релаксации резко меняется в окрестности 400 К (вставки на рис. 1). Ниже Т = 400 К в системе существует одно время релаксации в области частот 102–106 Гц и компоненты импеданса описываются в модели Дебая:

Im Z ( го ) =

B гот

1 + ( гот )² ,

где τ – время релаксации носителей тока; B – параметр. Выше 420 К в системе появляется спектр времен релаксации. Время релаксации от температуры зависит экспоненциально τ = τ0·exp(Eg/T) c энергией активации Eg = 0,47 эВ в (MnSe)1–x(Tm0,76Se)x для х = 0,05.

О

E

E

b

10-2

10-3

10-4

300  400  500

T, K

го , Hz

го , Hz

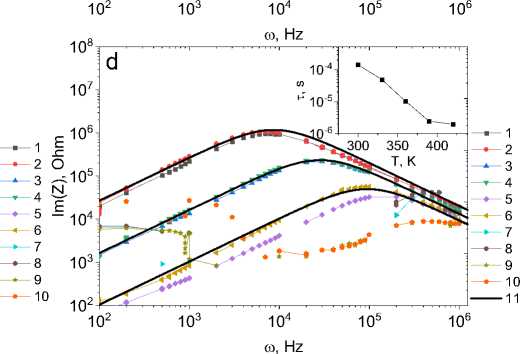
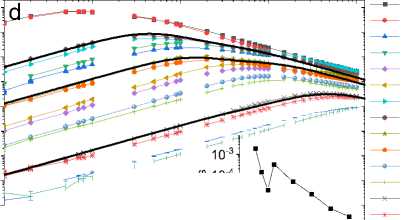
Рис. 1. Частотные зависимости импеданса Z ( a , c ) и мнимой части импеданса ( b , d ) для образцов Tm 0,05 Mn 0,95 S ( a , b ), измеренные в нулевом магнитном поле (1, 3, 5, 7, 9) и в поле 8 кЭ (2, 4, 6, 8, 10) при Т = 300 (1, 2), 350 (3, 4), 400 (5, 6), 450 (7, 8), 500 К (9, 10), и для образцов Tm 0,04 Mn 0,95 Se ( c , d ), измеренные в нулевом магнитном поле (1, 3, 5, 7, 9) и в поле 12 кЭ (2, 4, 6, 8, 10) при Т = 300 (1, 2), 330 (3, 4), 360 (5, 6), 390 (7, 8), 420 К (9, 10). Вставки: температурные зависимости времени релаксации τ. Результаты эксперимента описаны в рамках модели Дебая (сплошные линии 11)

Fig. 1. Frequency dependences of impedance Z ( a , c ) and imaginary part of impedance ( b , d ) for Tm_0.05Mn_0.95S samples ( a , b ) measured in zero magnetic field (1, 3, 5, 7, 9) and in a field of 8 kOe (2, 4, 6, 8, 10) at T = 300 (1, 2), 350 (3, 4), 400 (5, 6), 450 (7, 8), 500 K (9, 10) and for Tm 0.04 Mn 0.95 Se samples ( c , d ) measured in zero magnetic field (1, 3, 5, 7, 9) and in a field of 12 kOe (2, 4, 6, 8, 10) at T = 300 (1, 2), 330 (3, 4), 360 (5, 6), 390 (7, 8), 420 K (9, 10). Inserts: temperature dependences of the relaxation time τ. The experimental results are described within the Debye model (solid lines 11)

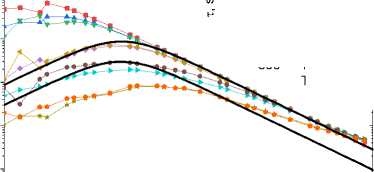
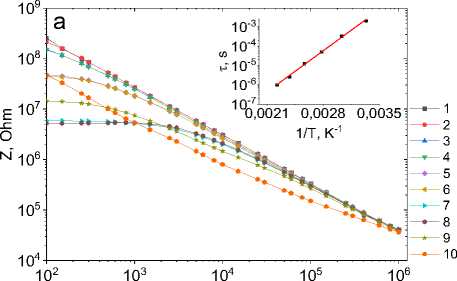
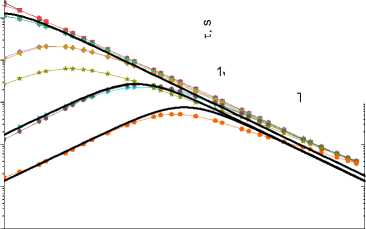
Компоненты импеданса от частоты в Tm 0,1 Mn 0,9 S (рис. 2, а ) можно описать в модели Дебая с одним временем релаксации, которое имеет активационный вид до Т = 450 К с энергией активации E g = 0,72 эВ (вставка на рис. 2, b ). В (MnSe) 1–x (Tm 0,76 Se) x с х = 0,1 Im(Z(ω)) хорошо описывается в модели Дебая:

Im Z ( го ) =

A гот1

1 + ( гот 1 )²

B гот ₂ +

1 + ( гоТ 2 )

с двумя временами релаксации (рис. 2, с ) и с энергией активации E g = 0,6 эВ для τ 1 меньше, чем в Tm 0,1 Mn 0,9 S.

n

E

b

350 400 450 500

T, K

10-3

10-4

10-5

10-1

10-2

E 107

O R

—■—1

—♦—2

--A3

--▼4

--<6

--►7

--•8

--• 10

ω , Hz

E

О

10-2

n

E

10-3 102

ω , Hz

Рис. 2. Частотные зависимости импеданса Z ( a , c ) и мнимой части импеданса ( b , d ) для образцов Tm 0,1 Mn 0,9 S ( a , b ), измеренные в нулевом магнитном поле (1, 3, 5, 7, 9) и в поле 8 кЭ (2, 4, 6, 8, 10) при Т = 300 (1, 2), 350 (3, 4), 400 (5, 6), 450 (7, 8), 500 К (9, 10), и для образцов Tm 0,08 Mn 0,9 Se ( c , d ), измеренные в нулевом магнитном поле (1, 3, 5, 7, 9, 11, 13, 15) и в поле 12 кЭ (2, 4, 6, 8, 10, 12, 14, 16) при Т = 300 (1, 2), 310 (3, 4), 320 (5, 6), 330 (7, 8), 360 (9, 10), 390 (11, 12), 420 (13, 14), 450 К (15, 16). Вставки: температурные зависимости времени релаксации τ. Результаты эксперимента описаны в рамках модели Дебая (сплошные линии 11, 17)

---1--- 16

ω , Hz

10-1

300 350 400 450

T, K

” 10-4

10-5

10-6

10^{6      17}

ω , Hz

Fig. 2. Frequency dependences of impedance Z ( a , c ) and imaginary part of impedance ( b , d ) for Tm 0.1 Mn 0.9 S samples ( a , b ) measured in zero magnetic field (1, 3, 5, 7, 9) and in a field of 8 kOe (2, 4, 6, 8, 10) at T = 300 (1, 2), 350 (3, 4), 400 (5, 6), 450 (7, 8), 500 K (9, 10) and for Tm_0.08Mn_0.9Se samples ( c , d ) measured in zero magnetic field (1, 3, 5, 7, 9, 11, 13, 15) and in a field of 12 kOe (2, 4, 6, 8, 10, 12, 14, 16) at T = 300 (1, 2), 310 (3, 4), 320 (5, 6), 330 (7, 8), 360 (9, 10), 390 (11, 12), 420 (13, 14), 450 K (15, 16).

Inserts: temperature dependences of the relaxation time τ. The experimental results are described within the Debye model (solid lines 11, 17)

Re[ ε _xx ( ω )] =

ε (1 -β ² + ( ωτ )²(1 +β ²)²)

1 + ( ωτ )²(1 + β ²)²

где β = μН, μ – подвижность, τ = RC. Относительное изменение импеданса [23]

( Z ( H ) - Z (0)) ₌ ( ε (0) -ε ( H )) ₌        β ²

Z ( H )            ε (0)       1 + ( ωτ )²(1 + β )²

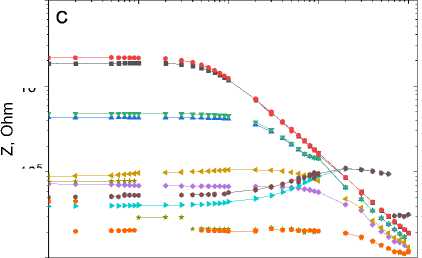
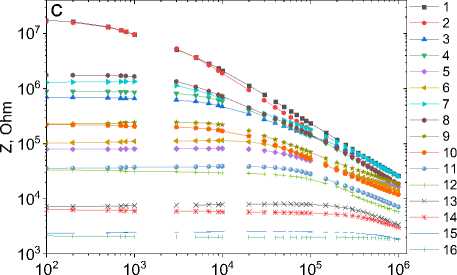
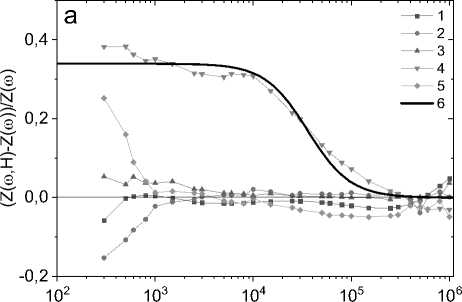
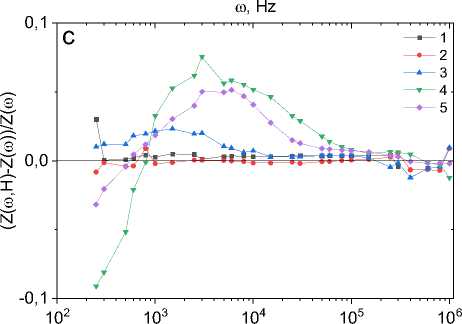
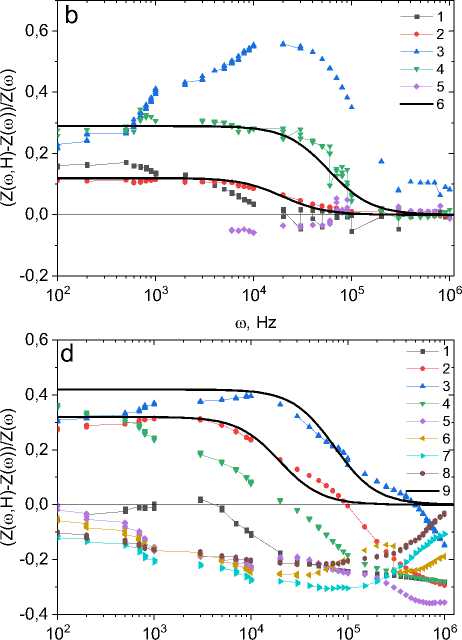
и его компонент удовлетворительно описывается этой функцией в области малых концентраций (рис. 3). В результате из импеданса можно получить информацию об электрической неоднородности [24] и диэлектрической проницаемости в среде [25; 26].

ω, Hz

Рис. 3. Магнитоимпеданс в магнитном поле H = 8 кЭ при температурах T = 300 (1), 350 (2), 400 (3), 450 (4), 500К (5) для образцов Tm_0,05Mn_0,95S ( a ); в магнитном поле H = 12 кЭ при температурах T = 300 (1), 330 (2), 360 (3), 390 (4), 420 К (5) для Tm_0,04Mn_0,95Sе ( b ); в магнитном поле H = 8 кЭ при температурах T = 300 (1), 350 (2), 400 (3), 450 (4), 550 К (5) для образцов Tm_0,1Mn_0,9S ( c ); в магнитном поле H = 12 кЭ при температурах T = 300 (1), 310 (2), 320 (3), 330 (4), 360 (5), 390 (6), 420 (7), 450 К (8) для Tm_0,08Mn_0,9Sе ( d ). Результаты эксперимента описаны формулой (5) (сплошные линии 6, 9)

ω, Hz

Fig. 3. Magnetoimpedance in a magnetic field of H = 8 kOe at temperatures T = 300 (1), 350 (2), 400 (3), 450 (4), 500 K (5) for Tm_0.05Mn_0.95S samples ( a ); in a magnetic field of H = 12 kOe at temperatures T = 300 (1), 330 (2), 360 (3), 390 (4), 420 K (5) for Tm_0.04Mn_0.95Se ( b ); in a magnetic field of H = 8 kOe at temperatures T = 300 (1), 350 (2), 400 (3), 450 (4), 550 K (5) for Tm 0.1 Mn 0.9 S samples ( c ); in a magnetic field H = 12 kOe at temperatures T = 300 (1), 310 (2), 320 (3), 330 (4), 360 (5), 390 (6), 420 (7), 450 K (8) for Tm 0.08 Mn 0.9 Sе ( d ). The experimental results are described by formula (5) (solid lines 6, 9)

4. Заключение

В (MnSe)1–x(Tm0,76Se)x найдено превалирование реактивной части импеданса, в сульфиде Tm0,05Mn0,95S преобладает реальная часть импеданса. С ростом концентрации замещения мар- ганца тулием импеданс и его компоненты увеличиваются на порядок. Возможно образование зарядового упорядочения и увеличение емкости на два порядка. Релаксация носителей заряда описывается в модели Дебая. Найден активационный характер времени релаксации и энергия активации. Для малых концентраций импеданс увеличивается в магнитном поле в халькогенидах. С ростом концентрации магнитоимпеданс меняет знак по частоте и температуре. Увеличение импеданса в поле вызвано уменьшением диэлектрической проницаемости в магнитном поле.

Работа поддержана Российским научным фондом, Правительством Красноярского края и проектом Красноярского научного фонда № 23-22-10016.

Acknowledgements

The study was supported by a grant from the Russian Science Foundation Nо. 23-22-10016, the Krasnoyarsk Regional Science Foundation.