Магнитоэлектрический эффект, индуцируемый орбитальным упорядочением электронов

Исследование мультиферроиков, в которых сосуществует хотя бы два из трех параметров порядка: магнитный, электрический или кристаллографический [1], является актуальной задачей, так как описывает возможность с помощью электрического поля управлять магнитными свойствами материала и, наоборот, осуществлять модуляцию электрических свойств магнитным полем. В перспективе такие материалы могут найти широкое техническое применение в качестве сенсоров, датчиков, устройств записи-считывания информации. Если в спиновой электронике запись информации происходит путем преобразования намагниченности в электрическое напряжение, то в мультиферроиках связь между магнитной и электрической подсистемами проявляется через магнитоэлектрический эффект [2; 3].

Твердые растворы CoxMn1–xS можно отнести к классу мультиферроиков [4]. В области температур Т = 230 К обнаружена корреляция между упругой, магнитной и электрической подсистемой. Это подтверждается следующими фактами: найдено изменение угла наклона постоянной решетки, сдвиг пика поглощения рамановской моды, зависимость от предыстории температурного поведения намагниченности и сопротивления при «отжиге» в магнитном поле, нелинейной зависимостью вольт-амперной характеристики в магнитном поле, и наличие максимума в изменении диэлектрической проницаемости во внешнем магнитном поле от температуры [5]. На взаимодействие между электрической, магнитной и уп- ругой подсистем при температурах Т = 120 К указывает также образование ферромагнитного порядка, максимум по температуре относительного изменения диэлектрической проницаемости, измеренной во внешнем магнитном поле и в отсутствие поля [6], аномалия коэффициента теплового расширения решетки.

Предполагается, что замещение ионов марганца кобальтом приводит к перераспределению электронной плот ности между e _g- и t_2g-состояниями. Конкуренция кулоновского взаимодействия между электронами, расположенными на одной орбитали и между орбиталями, совместно с изменением интегралов перескока приводит к упорядочению электронов на определенных орбиталях и к орбитальному магнетизму. В результате перераспределения электронной плотности меняется упругая энергия и под действием электрон-фононного взаимодействия индуцируются связанные моды колебаний ионов.

Цель работы состоит в установлении взаимосвязи между магнитной, электрической и упругой подсистемами и определении тенденций изменения параметров решетки, величины корреляционных функций орбитальных и спиновых моментов в зависимости от параметра электрон-решеточного и спин-фононного взаимодействия.

Модель взаимосвязи электронной и упругой подсистем. Для интерпретации полученных результатов в твердом растворе CoxMn1–xS [5; 6] необходимо рассматривать взаимосвязь электронной и кристаллической струк- тур. Ион кобальта содержит на два электрона больше в t2g-оболочке, чем ион марганца. В этом случае перескоки между соседними узлами и разными орбиталями совершаются без изменения кулоновского взаимодействия электронов. Кроме того, увеличивается кинетическая энергия электронов вследствие образования узкой минизоны в окрестности уровня Ферми, сформированной в результате перескока электронов по ближайшим ионам марганца.

Для пары ионов марганца с наполовину заполненными орбиталями интеграл перескока электронов через анион серы можно оценить по формуле Св = E x ,a E x ,e / ^{[( e} p ⁸ d ) ⁺ U ], где Е a ^- интегралы пере крытия p-орбиталей серы и t_2g-орбиталей марганца, имеющих величину Е б = 1,1 eV; e _p- 8 d = 1,5 eV - величина зарядовой щели; U = 4 eV. Для двух электронов на одном из пяти d-уровней ионов марганца в окружении ионов серы интеграл перекрытия равен нулю Е х a = 0 в силу принципа Паули, и при поперечных колебаниях ионов серы возможно слабое перекрытие электронных волновых функций ионов марганца с шириной минизоны W = 2zt = 0,5 – 0,8 eV. Таким образом, транспортные свойства связаны с перескоком дырки по e_g-орбиталям и с движением электронов по t_2g-состояниям. Тип носителей соответствует решеточным поляронам, т. е. движение электронов по решетке индуцирует связанные поперечные и продольные колебания ионов серы и реализуется по одной из подзон t_2g-зоны, обладающей орбитальным магнитным моментом, а в e_g-зоне движение носителей тока непосредственно связано с типом магнитной структуры. В результате индуцируется разная заселенность d_xy-, d_xz-, d_yz-орбиталей и образуется орбитальнозарядовое упорядочение, сопровождающееся упорядочением орбитальных угловых моментов.

Гамильтониан в феноменологическом представлении для двух орбиталей, обозначим их через x , y , и двух узлов можно записать в виде

H = - J 1⁽ n 1 x ^- n 1 y ⁾⁽ n 2 x ^- n 2 y ^{)(1 -} c ) ^-

- g ⁽ n 1 x ⁺ n 2 x ⁾⁽¹ - c ) x ^- g ⁽ n 1 y ⁺ n 2 y ⁾⁽¹ - c ) У ⁺

+ 2 k ( x ² + y ²) - b ( x ³ + y ³) - h ( n 1 _x + n 2 _x -

^- n 1 y ^- n 2 y ^{)(1 -} c ) ^- J 2⁽ n lix ^- n liy ⁾⁽ n 2ix ^- n 2iy ) c ^-

- KM 1 M 2 - gs (x + y) M 1 M 2 - X (1 - с )( n1 x - n1 y )x xM1 - X (1 - с) (n 2 x - n 2 y) M 2 - h (M1 + M 2) -

^- h ⁽ n 1x ^- n 1 ,y ⁺ n 2ix ^- n 2iy ) c ^-

-сX ( n1x - n1,y ) M1 - X ( n2ix - n2iy ) M2c, где n1,2ix, n1,2x,y – электронная плотность на орбиталях dxz-, dyz-ионов марганца, окружающих ион кобальта, концентрация которого равна с, и на ионах марганца в матрице с концентрацией (1 – с); J1 и J2 – обменные взаимодействия между орбитальными магнитными моментами Mn–Mn и Сo–Mn; g – параметр электрон-решеточного взаимодействия; x, y – смещения ионов в направлениях, соответствующих сторонам квадрата; k, b – упругие константы; h – магнитное поле; а – постоянная решетки; K < 0 – обменное взаимодействие между магнитными моментами М1 и M2; gs – константа спин-решеточного взаимодействия; X - параметр спин-орбитальной связи. При взаимодействии орбитальных и спиновых моментов возникают члены более высокого порядка (L1L2) и (M1M2), но для t2g-электронов они существенно меньше спин-ор-битального взаимодействия.

В рамках такого гамильтониана мы попытаемся ответить на несколько вопросов. Как влияет концентрация кластеров Mn–Co–Mn и эффективное орбитальное взаимодействие на температуру образования спонтанного магнитного момента. Каким образом будет меняться параметр решетки при орбитально-зарядовом упорядочении, при магнитном упорядочении? К каким изменениям в температурном поведении орбитальных корреляционных функций (соответственно перераспределение заряда) приводит внешнее магнитное поле?

Электронную плотность на t_2g-орбиталях ионов марганца в матрице оценим из величины спинового момента на узле S = 4,4 м_B для MnS, т. е. n _1,2 ~ 0,1, а электронная плотность в кластере Mn–Co может достигать величины n _{1,2 i} ~ 0,5.

Термодинамические характеристики, корреляционную функцию между ближайшими соседями для орбитальных < L ₁ L ₂>, L = n _{1 x} – n _{1 y} и магнитных < M ₁ M ₂> моментов, среднюю величину смещения по осям ОХ < x > и ОУ < y > вычислим в непрерывной модели Потса, где соответствующие величины меняются в интервалах 0 <  n _{1,2 x , y} < 0,1 и 0 <  n _{1,2 ix} < 0,5, 0 <  x , y < 1, –1 <  M _1,2< 1. ^{, ,}

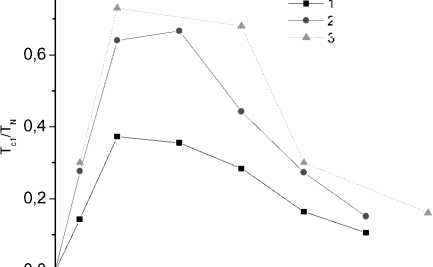
Термодинамические характеристики модели. Коррелятор магнитных моментов в области температуры перехода из магнитоупорядоченной фазы в парамагнитную уменьшается в два-три раза и имеет точку перегиба. Поэтому температуру, при которой исчезает дальний ферромагнитный порядок орбитальных моментов, ассоциируем с температурой, при которой наблюдается перегиб в температурной зависимости корреляционных функций < L ₁ L ₂> ( Т ) и < M ₁ M ₂> ( Т ). Рассмотрим температурные зависимости корреляторов для ряда концентраций ионов кобальта (рис. 1), где можно выделить две температуры, при которых упорядочиваются орбитальные магнитные моменты ионов марганца при T_c и орбитальные моменты кластеров Mn–Co–Mn при Т_{с 1}. Типичное концентрационное поведение Т_{с 1} (c) (рис. 2) для двух параметров обмена J ₂/ J ₁ коррелирует с концентрацией кластеров Mn–Co–Mn в зависимости от концентрации кобальта, вычисленных как с = zx (1– x ) ^{z –1} ( z – число ближайших соседей для ГЦК решетки, z = 12). Согласно нашим расчетам, зависимость Т_{с 1} от величины обмена между орбитальными магнитными моментами в кластере Mn–Co–Mn линейна, где угол наклона зависит от концентрации ионов кобальта и электрон-решеточного взаимодействия, которое сдвигает температуру перехода упорядочения орбиталей в сторону высоких температур в пределах 20 % при увеличении g / J ~ 1. Экспериментальные результаты (рис. 1, 2) удовлетворительно описываются в модели с орбитальным упорядочением угловых моментов.

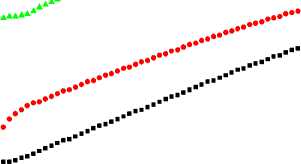
Рассмотрим влияние электрон-решеточного и спин-решеточного взаимодействия на деформацию решетки и изменение постоянной решетки с температурой (рис. 3). Даны зависимости величины среднего смещения ионов от температуры для ряда параметров электрон-решеточ-ного и спин-решеточного взаимодействий с учетом ан-горманизма колебаний решетки (рис. 3, а). Взаимодействие электронов с учетом решеточных степеней свободы приводит к увеличению расстояния между электронами, т. е. к росту постоянной решетки. Так, смещение прямо пропорционально константе электрон-фононно-го взаимодействия = gn/k в системах с сильными электронными корреляциями, когда кулоновское взаимодействие превышает ширину зоны, в пренебрежении ангор-манизмом колебаний. С ростом величины электрон-ре-шеточного взаимодействия наблюдается изменение величины наклона при некоторой температуре, которая сдвигается в область высоких температур с ростом параметра g.

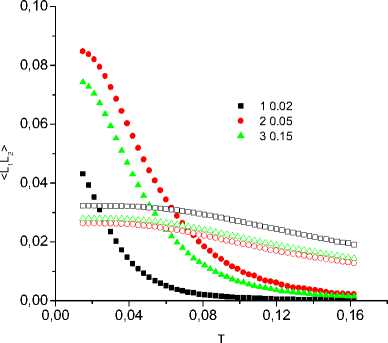
Рис. 1. Корреляционная функция магнитных орбитальных < L ₁ L ₂> моментов в матрице из ионов марганца (светлые символы) и в кластере Mn–Co–Mn (темные символы) в зависимости от температуры для J ₁ = 10, J ₂ = 6, g = 6, k = 20, b = 3, K = –0,35, g _s = 0,1, λ = 0,1, x = 0,02 (1), 0,05 (2), 0,15 (3)

0,8

0,0

0,1

0,2

0,3

,

Рис. 2. Температура формирования орбитального магнитного момента в кластере Mn–Co–Mn, нормированная на температуру Нееля, для ряда параметров J ₂ = 5 (1), 8 (2), J ₁ = 10, g = 6, k = 20, b = 3, K = –0,35, g_s = 0,1, λ = 0; эксперимент (3) от концентрации кобальта

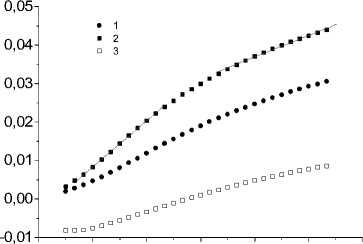
Обменное взаимодействие между локализованными спинами имеет экспоненциальную зависимость от рас- стояния, в результате сжатия решетки плотность перекрытия волновых функций электронов растет и возрастает энергия обмена. Увеличение спин-решеточной связи приводит к смене знака средней величины смещения ионов (рис. 3, б). В результате конкуренции электрон-ре-шеточных и спин-решеточных взаимодействий решетка сжимается. Изменение наклона зависимости d/dT наблюдается в области перехода в магнитоупорядоченное состояние.

0,020

0,016

0,012

0,008

0,004

■ 1

• 2

▲ 3

0,00   0,03   0,06   0,09   0,12   0,15   0,18

T а

T

0,00    0,03    0,06    0,09    0,12    0,15    0,18

T б

Рис. 3. Величина среднего смещения иона < x > от температуры для ряда параметров электрон-фононного взаимодействия g = 2 (1), 5 (2), 8 (3) c b = 1, J ₂ = 6, J ₁ = 10, k = 20, K = –0,35, g_s = 0,1, л = 0, x = 0,15 ( a ) и для двух параметров спин-фононного взаимодействия g_s = 0,1, x = 0,02 (1), x = 0,05 (2), g_s = 0,2, x = 0,05 (3) c J ₁ = 10, J ₂ = 6, g = 6, k = 20, b = 3, K = –0,35, λ = 0,1 ( б )

Флуктуации спиновых магнитных моментов в двух подрешетках ассиметричны при наличии спин-орбиталь-ного взаимодействия, в результате индуцируется суммарный магнитный момент ( M ₁ + M ₂) с максимумом при температуре Нееля. Магнитный момент и постоянные решетки зависят от температуры (рис. 4). Взаимодействие орбитальных и спиновых моментов аналогично действию внешнего магнитного поля h_ef = λ < L >, когда меняется величина намагниченности одной из подрешеток (рис. 4, а ). Перераспределение электронной плотности на d_xz -, d_zy -орбиталях является причиной возникновения тетрагонального искажения (рис. 4, б ).

Изменение электронной плотности на e_g- и t_2g-состо-яниях индуцирует электронную поляризацию иона, которая определяется поляризуемостью атома a = a _n + 2 b_n

[M2J –1/3 J(J + 1)], где an, bn – постоянные; J – полный момент атома; МJ – проекция момента на выделенное направление. Диэлектрическая проницаемость связана с поляризуемостью ε = 1 + 4πNa, и изменение диэлектрической проницаемости во внешних магнитных и электрических полях определяется как Δε ~Δa~ΔM2J ~ Δ . Перестройка орбитальной структуры магнитным или электрическим полями проявится в изменении корреляционных функций (рис. 5). Первый максимум в области низких температур обусловлен изменением орбитальной корреляционной функции в кластере Mn–Co, а второй связан с ростом орбитального порядка в марганцевой системе. Это качественно объясняет наличие двух максимумов в магнитоэлектрическом эффекте. Аналогичное поведение наблюдается во внешнем электрическом поле в результате изменения электронной плотности на орбиталях вследствие зависимости потенциальной энер-

Конкуренция кулоновского взаимодействия между электронами, расположенными на одной орбитали и между орбиталями, совместно с изменением интегралов перескока приводит к упорядочению электронов на определенных орбиталях и к орбитальному магнетизму. Электрон-фононное взаимодействие приводит к расширению решетки, а спин-фононное – к сжатию решетки. В результате конкуренции орбитального и спинового упорядочения вычислена величина тетрагонального искажения в зависимости от температуры. Оценена величина магнитоэлекрического эффекта.

гии электрона от расстояния во внешнем однородном электрическом поле. Существенный вклад в диэлектри- ческую проницаемость дает также ян–теллеровское смещение ионов, которое не учитывается в данной модели.

0,035

0,030

0,025

0,020 s' .

s 0,015

0,010

0,005

0,000

■   1

♦ 2

▲ 3

0,00        0,04        0,08        0,12        0,16

0,00        0,03        0,06        0,09        0,12

T/J

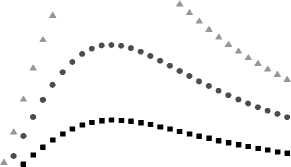
Рис. 5. Разность корреляционных функций орбитальных магнитных моментов для кластеров Mn–Co–Mn (левая шкала) и для ионов марганца (правая шкала), вычисленных в магнитном поле и без поля, от температуры для

J ₁= 10, J ₂= 5, g = 6, k = 20, b = 3, K = –0,35, g_s = 0,1, λ = 0,1, x = 0,02 (1), 0,05 (2), 0,15 (3)

0,010

0,005

0,000

0,00

T/J а

0,04         0,08         0,12         0,16

T/J б

Рис. 4. Общая намагниченность спиновых моментов (M₁+M₂) ( а ) и величина тетрагонального искажения решетки < x – y > ( б ) в зависимости от температуры для ряда параметров спин-орбитального взаимодействия λ = 0,1 (1), 0,2 (2), 0,3 (3) с J ₁= 10, J ₂= 5, g = 6, k = 20, b = 3, K = –0,35, g _s = 0,1, x = 0,05