Магнитоэлектрический эффект в Mn1-xCoxS

Исследование мультиферроиков, в которых сосуществует хотя бы два из трех параметров порядка: магнитного, электрического или механического, является актуальной задачей, так как предоставляет возможность с помощью электрического поля управлять магнитными свойствами материала и, наоборот, осуществлять модуляцию электрических свойств магнитным полем. В перспективе такие материалы могут использоваться в качестве сенсоров, датчиков, устройств записи-считывания информации. Если в спиновой электронике преобразование информации происходит через изменение намагниченности в электрическое напряжение, то в мультиферроиках связь между магнитной и электрической подсистемами проявляется через магнитоэлектрический эффект [1].

К мультиферроикам относятся бораты [2], гексагональные манганиты [3], сегнетомагнетики [4], например, феррит висмута BiFeO3 [5], у которого температура Кюри ферроэлектрического фазового перехода превышает температуру магнитного фазового перехода. Для семейства манганитов RMn2O5 [6] магнитный и ферроэлектрический порядок образуются при близких температурах. Возможный механизм перехода связан с Ян–Теллеровским ионом Mn+3 и превалирующим спин-орбитальным взаимодействием, индуцирующим нарушение инверсионной симметрии. Неинвариантность относительно центра инверсии может быть образована топологией магнитной структуры. Так, в Gd2CuO4 [7] спины ионов меди упорядочиваются антиферромагнитно в базисных плоскостях тетрагональной кристаллической решетки, а спины ионов гадолиния образуют ферромагнитные слои, намагниченные параллельно базисным плоскостям. В результате медная и гадолиниевая подсистемы оказываются обладают различной магнитной симметрией.

В данной работе рассматриваются магнитоэлектрические эффекты, возникающие в результате электрон-фо-нонного взаимодействия электронов 3d-элементов с упругими модами колебаний. В твердом растворе Mn1–xCoxS наличие дырки в t2g-уровне двухвалентного иона кобальта в октаэдрическом окружении обусловливает вырождение, которое снимается в результате взаимодействия с акустическими фононами, а резонансное взаимодействие с одной из мод октаэдра приводит к связанному электрон-фононному состоянию, которое вырождено в импульсном пространстве.

Межорбитальное кулоновское взаимодействие между электронами индуцирует флуктуации электронной плотности на d_xy-, d_xz-, d_yz- орбиталях в ионах кобальта, имеющих в ближайшем окружении только ионы марганца. В результате возникает орбитальный магнитный момент на узле, хаотически распределенный по решетке в области высоких температур. Взаимодействие орбиталей через акустические моды колебаний приводит к их ферромагнитному упорядочению и к изменению величины интегралов перескока Co–S–Mn, что вызывает изменение расстояния Co–Mn в кубическом кристалле из-за взаимодействия с одной из мод колебаний октаэдра. Под действием внешних полей, магнитного или электрического, вырождение по направлению гибридизации связей Co– Mn снимается.

Цель данной работы заключается в установлении взаимосвязи между орбитальным магнитным упорядочением, наблюдаемым нами ранее [8], и электрическим состоянием в результате измерения действительной и мнимой части диэлектрической проницаемости во внешних электрических и магнитных полях.

Технология приготовления образцов описана в работе [8]. Реальная и мнимая части диэлектрической проницаемости измерены в области температур 80 K <  T <  300 K на трех частотах f = 1, 10, 100 кГц как в магнитном, так и в постоянном электрическом поле в зависимости от пре-дистории образца.

Температурные зависимости диэлектрической проницаемости, измеренные на частоте f = 1 кГц для Mn_{1 –x} Co _x S, к которому приложено постоянное внешнее электрическое поле изображены на рис. 1.

С ростом поля реальная часть диэлектрической проницаемости уменьшается, а ее мнимая часть растет, особенно отчетливо это наблюдается при T >  200 K (вставка на рис. 1). При нагревании меняется характер частотной зависимости диэлектрической проницаемости (рис. 2) при некотором значении температуры Т *, соответствующей пересечению кривых ε ( Т ), измеренных на разных частотах. С ростом поля эта температура уменьшается от Т* = 220 K, E = 0 до Т* = 175 K, E = 50 В/см .

При T ~ 120 K на частоте f = 100 кГц наблюдается небольшой максимум диэлектрической проницаемости, который наиболее отчетливо проявляется при вычислении производной d ε ( T ) /dT. Постоянное магнитное поле также меняет величину диэлектрической проницаемости в сторону ее уменьшения.

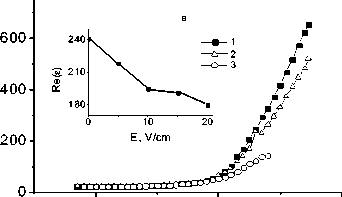
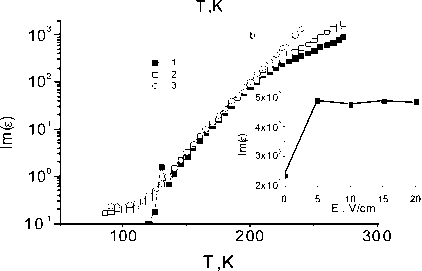
Рис. 1. Реальная (Re( ε ))(а) и мнимая (Im( ε )(b) части диэлектрической проницаемости от температуры, измеренные на частоте f = 1 кГц при разных величинах электрического поля Е = 0 (1), 5 В/см (2), 50 В/см (3). На вставках: зависимость Re( ε ) и Im( ε ) при температуре T = 260 K

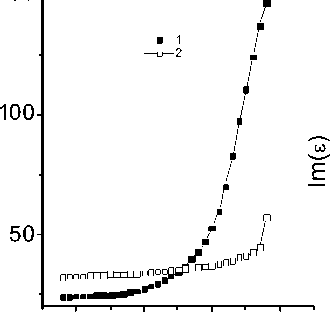
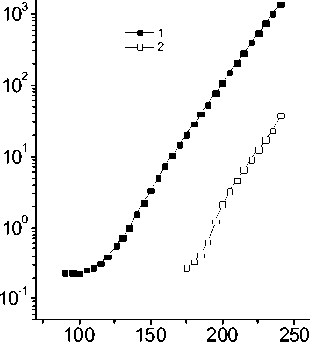
Относительные изменения диэлектрической проницаемости, измеренные в нулевом магнитном поле и в поле H = 5 кЭ приведены на рис. 3. Найдено два максимума в (ε(Н = 0,T) – ε (Н, Т))/ε(Н, Т)) при T1 ~ 125 K и T2 ~ 225 K. Величина магнитоэлектрического (MЭ) эффекта составляет 3 %, а мнимая часть ε(Т) уменьшается в магнитном поле в десятки раз при Т ~ 110 K. Величина МЭ эффекта в постоянном электрическом поле E = 5 В/см возрастает на порядок при T ~ 225 K, а мнимая часть резко падает на два порядка при T ~ 110 K. Температуры Т = 110, 125 K, соответствующие максимумам магнитоэлектрического эффекта, коррелируют с температурой, при которой образуется слабый спонтанный магнитный момент в Mn1–xCoxS [8], в результате ферромагнитного упорядочения орбитальных магнитных моментов.

Описанные выше эффекты можно объяснить в модели орбитально-зарядового упорядочения. Кулоновское взаимодействие между электронами, находящимися на разных t_2g- орбиталях, понижает энергию в случае разной заселенности орбиталей и приводит к расщепелению уровней

В результате возникает пространственная анизотропия интегралов перескока между соседними ионами кобальта и марганца через анион серы (рис. 4).

При половинном заполнении орбиталей перенос электронной плотности между соседними узлами связан с сильным кулоновским отталкиванием электронов на узле ( U ) и эффективный интеграл перескока электронов между соседними катионами вдоль оси x через анион серы приводит к выражению t^x_ab = E_x,aE_x,b/ ( e_p – e_d + U ), где е_р, e_d энергия уровней для p - и d- орбиталей, E_xа – интеграл перекрытия между t _{2 g}- и p_x- орбиталями, соответственно, для ионов Co^{2 +} , Mn^{2 +}. Для данной электронной конфигурации (рис. 4), интеграл переноса в направлении оси Y , имеет меньшую величину из-за сильного кулоновского отталкивания электронов на узле ( U ) и отличается практически в два раза ( t^x – t^y )/ t^x = U /( e_p – e_d ) . Неоднородное распределение электронной плотности по t _{2 g}- состояниям индуцирует орбитальный магнитный момент L^z = n _a – n _β , ( a , β = d yz , d_xz ), где n _a , n _β – числа заполнения электронов на соответствующих орбиталях.

На решетке (рис. 4) схематично представлено случайное распределение ионов кобальта по решетке с орбитальным моментом, направленным вверх и вниз и с сильным обменным взаимодействием между парой ближайших ионов марганца. Сильная величина ковалентной связи приводит к деформации октаэдра и к упругим искажениям в решетке. То есть электроны, локализованные в

100 150   200   250

T,K а                    б       ^T,K

Рис. 2. Реальная ( а ) и мнимая ( б ) части диэлектрической проницаемости от температуры, измеренные на частотах f = 1 кГц (1), 100 кГц (2) во внешнем постоянном электрическом поле Е = 50 В/см

кластере, взаимодействуют между собой посредством акустических и оптических мод колебаний, которые можно описать электрон-фононным взаимодействием. Среднее расстояние между ионами кобальта, находящимися только в окружении марганца l/a = 1/ c ^1/3 , тогда модуль волнового вектора Q = 2 √ 3 π /l = 2 √ 3 π c ^1/3, где концентрация соответствующих кластеров в ГЦК-решетки равна c = 12 x (1 – x )¹¹ и для концентрации x = 0,05 соответствует волновой вектор Q = 2 √ 3 π /3. В результате взаимодействия электронов с акустической и оптической модами колеба-

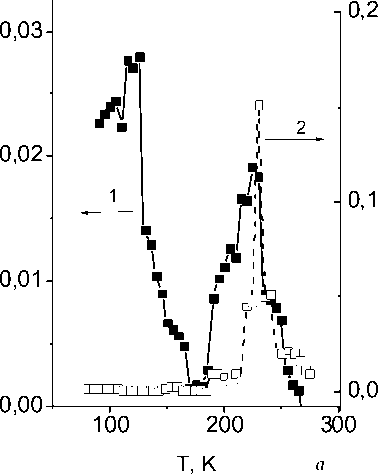
Рис. 3. Относительное изменение реальнай ( а ) и мнимой ( б ) части диэлектрической проницаемости в магнитном поле H = 5 кЭ от температуры на частоте f = 1 кГц в нулевом электрическом поле (1) и в поле E = 5 В/см (2)

б             T, K

ний с вектором Q возникает связанное состояние и в спектре возбуждений наблюдается расталкивание соответствующих мод.

При асимметричным расположении ионов серы относительно катиона образуется электрический диполь. Можно оценить энергию взаимодействия между диполями во втором порядке теории возмущений по параметру элект-рон-фононного взаимодействия H _eph ~ (dt_ij/du_i)u_ic_i⁺ c_j либо с нелокальным диагональным взаимодействием ~ ^g

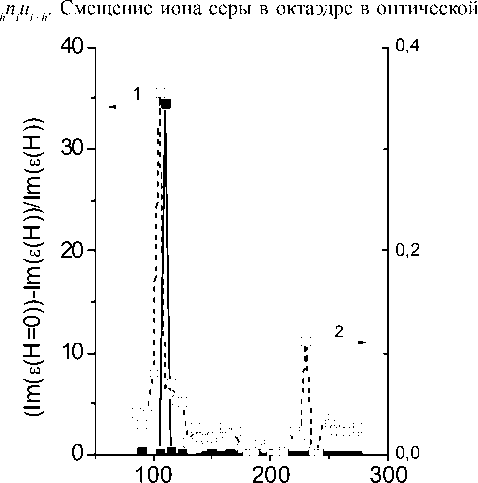
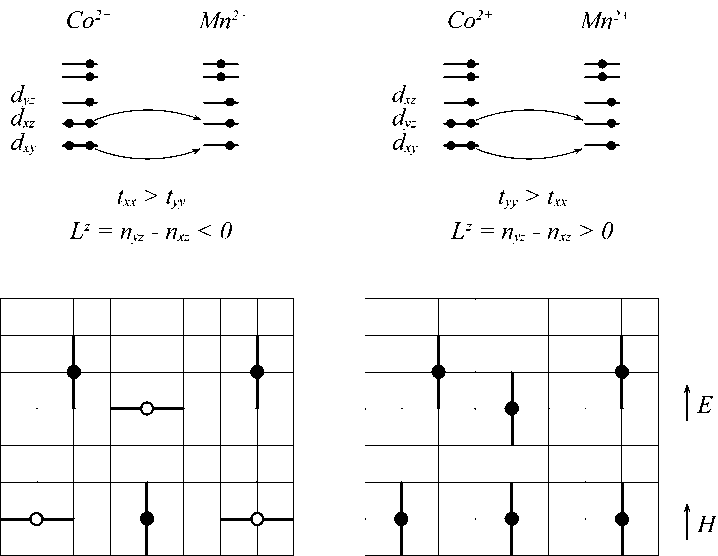
Рис. 4. Анизотропия интегралов перескока Co–Mn, обусловленная межорбитальным кулоновским взаимодействием. Схема распределения сильных обменных взаимодействий между электронами на парах Co–Mn (двойная линия) и орбитальных магнитных моментов, направленных вверх (точки) и вниз (пустые кружки) на решетке

моде колебаний приводит к нарушению операции центра инверсии и индуцирует локальный дипольный момент P = ( u_i – u_j ) n_i , где u_i = y_i – y_{i + h} , где y – локальное смещение иона на узле. При акустических колебаниях можно пренебречь слабой зависимостью корреляторов <  u_iu_{i + h} > от расстояния и для оценки ограничиться idh u_{i + h}>~< u²> , тогда при суммировании во втором порядке теории возмущений можно получить скалярное произведение орбитальных магнитных моментов и дипольных электрических моментов ионов, где наибольшим параметром является энергия зарядовой щели и кулоновское межорбитальное взаимодействие Δ = e_p – e_d + U_o . Эффективный гамильтониан имеет вид

H = – Σ JLL – Σ KPP , _{i , j}ij ij i j _{i , j} ij ij i j

J_ij=(dt/du_a)²< u² > / Δ ; K_ij = (dt/du_o)²/ Δ .       (1)

Взаимодействие между электрическими дипольными моментами и орбитальными магнитными моментами появляется в четвертом порядке теории возмущений H_int ~ A_ijkl ( L_iL_j )( P_kP_l ). Полный гамильтониан с учетом взаимодействия между подсистемами, так и с внешними магнитным и электрическим полями имеет вид

H = – Σ JLL – Σ A ( LL )( PP ) – _{i , j}ij ij i j _{i , j} ijkl ijkl i j k l

– Σ KPP – Σ ( HL+EP ),          (2)

• _{i ,    j}ij ij i j _{i ,} ji           i i

где H и Е соответственно магнитное и электрическое поле. Электрические диполи образуют несоразмерную структуру с вектором Q , который вырожден в ГЦК-решетке. Это вырождение при нагревании снимается и исчезает упорядочение диполей, сопровождающееся максимумом в диэлектрической проницаемости и диэлектрической восприимчивости. Качественную зависимость χ ( T ) можно оценить в модели Шотки χ ~ 1/T exp( –Kef/T ), где эффективное взаимодействие между диполями зависит от корреляционной функции орбитальных магнитных моментов Kef ~ K + A iL_j >. Тогда, разлагая экспоненту χ (0)/ χ ( H ) ~ exp( –A (( L_iL_j )( H = 0) – ( L_iL_j )( H )))/ T ) в ряд по малому параметру, получим оценку для относительного изменения диэлектрической проницаемости в магнитном поле ( ε ( Н ) – ε (0))/ ε ( H) ) ~ A (( L_i L_j ) ( H = 0) – ( L_iL_j )( H )))/ T. В области температур с упорядоченным расположением орбитальных магнитных моментов изменение корреляционной функции между ближайшими соседями стремится к нулю и имеет максимальное значение в окрестности перехода из магнитоупорядоченного состояния в парамагнитное. Так как существует две подсистемы с упорядочением орбитальных магнитных моментов между ионами кобальта и марганца с разными температурами упорядочения, что приводит к двум максимумам в температурной зависимости относительной диэлектрической проницаемости в магнитном поле (рис. 3).

При температурах Т > 200 K нелинейность диэлектрической проницаемости от внешнего электрического поля (вставка на рис. 1) обусловлена вырождением фурье образа дипольного момента P(Q) = 1/N Σ j exp(–iQrj)P(rj). Волновой вектор имеет шестикратное вырождение в импульсном пространстве. На рис. 5 даны значения Q(kx, k, kz), полученные при решении уравнения Q2 = (2πnx/La)2 +y + (2πny/La)2 + (2πnz/La)2 с L = 40 для двух значений кон- центраций. Внешнее электрическое поле приводит к асимметрии потенциальных ям и к понижению высоты потенциального барьера, разделяющих эти состояния, и в итоге при туннелировании результирующий дипольный момент увеличивается с ростом электрического поля, т. е. этот эффект аналогичен намагничиванию суперпарамагнитных частиц

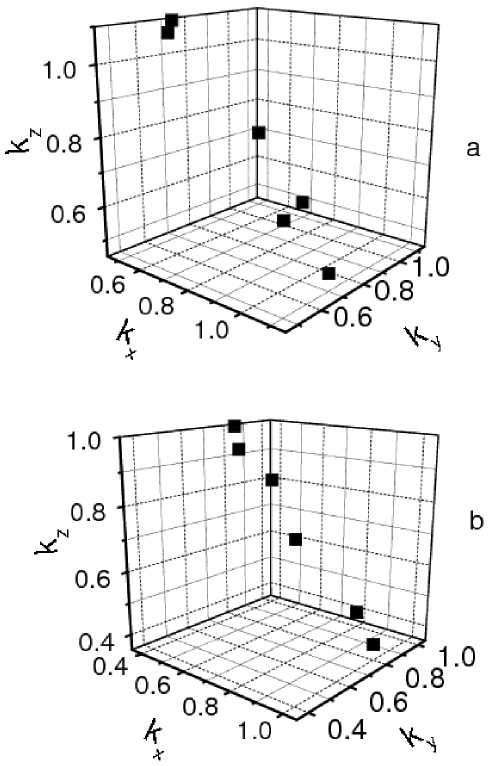
Рис. 5. Модуль волнового вектора Q = 2 √ 3 π c ¹/³ для электрического диполя P ( Q ), имеющего шестикратное вырождение в импульсном пространстве, для x = 0,05(a), 0,15(b)

Итак, в Mn_{1 –x} Co _x S обнаружен магнитоэлектрический эффект, имеющий максимальное значение при температурах T ~ 120 K и T ~ 230 K, величина которого увеличивается с ростом электрического поля. При T > 200 K найдена нелинейная зависимость диэлектрической восприимчивости от поля, характерная для суперпарамагнетиков. Экспериментальные данные объясняются за счет элект-рон-фононного взаимодействия дырки на t _{2 g}- орбиталях с акустическими и оптическими модами колебаний. В результате чего образуется связанное электрон-фононное состояние, которое конденсируется в одном из шести вырожденных состояний для электрического диполя с несоразмерным волновым вектором, модуль которого задается концентрацией ионов кобальта, имеющих в ближайшем окружении ионы марганца.