Магнитокалорический эффект в магнитоупорядоченных кристаллах. Состояние проблемы и перспективы технических приложений

Изложена теория магнитокалорического эффекта в кубическом, одноосном и поликристаллическом ферромагнетиках сучетом вращения намагниченности. Обсуждены вопросы создания новых холодилъныхмашин, использующих магнитокалорический эффект.

Магнитокалорический эффект (МКЭ) заключается в изменении температуры магнитного образца при изменении наложенного на него внешнего магнитного поля. Причиной этого эффекта является изменение магнитного состояния вещества и, следовательно, его внутренней энергии. МКЭ в парамагнетиках уже нашел широкое применение в технике криогенных температур, в то время как исследование МКЭ и его практическое применение в ферро- и ферримагнетиках требуют дальнейшего развития.

Измерение МКЭ в магнитоупорядоченных веществах может проводиться при двух принципиально различных условиях:

• -    при изменении напряженности магнитного поля без изменения его ориентации относительно образца;

• -    вращении магнитного поля относительно выделенных направлений в образце.

В первом случае для изотропного образца характерно изменение обменной энергии, во втором - изменение энергии магнитной анизотропии.

Первый эффект был открыт в 1918 г П. Вейссом и А. Пиккардом [1]. Для его описания в случае изотропного фер ромагнетика справедливо термодинамическое выражение a t = —

T f dM 1 a h , с I dT , ^c H V     J H

где М - намагниченность, АН - изменение магнитного поля; сн- удельная теплоемкость вещества. Отсюда следует, что приложение внешнего поля приводит к нагреву образца dM < 0 и этот эффект максимален вблизи тем- пературы Кюри.

Второй эффект был открыт в 1939 г. основателем и первым директором Института физики (г. Красноярск) академиком Л. В. Киренским при исследовании монокристаллического никеля и подробно описан в [2]. Для описания этого эффекта авторами [3] предложено выра использован для прямого преобразования механической энергии в тепловую. Анализу состояния исследования МКЭ и перспективам создания экологически чистых магнитных холодильных машин посвящены обзоры [4...7]. Особое внимание в них уделено редкоземельным металлам и их соединениям, где МКЭ достаточно большие значения. Заметим, что значительное место здесь занимает эффект Вейсса-Пиккарда, но при этом не учитываются процессы вращения намагниченности для изотропного ферромагнетика. Этот пробел в некоторой степени восполняют результаты исследований, изложенные в данной статье. Учет процессов вращения намагниченности позволяет дать иную формулировку принципов создания магнитных холодильных машин.

Анизотропия магнитокристаллического эффекта в ферромагнитных кристаллах. Рассмотрим эффект Вейсса-Пиккарда для случая одноосного и кубического ферромагнетиков [8].

Плотность свободной энергии одноосного кристалла во внешнем магнитном поле может быть записана в виде f = f о + к , а 2 + к 2 а ⁴ — ( MH ) ,          (3)

где/'. - не зависящая от магнитного упорядочения плотность свободной энергии; k₁ и k₂ - константы магнитной анизотропии; а - направляющий косинус вектора намагниченности относительно выделенной оси.

Равновесная ориентация вектора намагниченности находится по уравнению df / d а = 0 . Величина МКЭ определяется наклоном изоэнтропы на плоскости (Т, Н):

fA T 1 = ^{( д} S / d H ) т              (4)

(ah JS (дS / дт)H дf где s - энтропия, ^ = ^Т ■

Считая изменение температуры при МКЭ малым, можно ограничиться линейным разложением намагниченности и констант магнитной анизотропии по темпе жение

ратуре.

A Т = —

Т f dk 1

¹ А£а 2 а 2, с I dT , i j ^c

где k - первая константа магнитной кристаллографической анизотропии; а , а. - направляющие косинусы намагниченности относительно главных осей кристалла.

( к , sin 2 6 + 4 к ₂ sin ³ 6 cos

X-

f^ T 1 = T- X

(a h J ₅   c h

M ^ — к , —L 4sin ³ 6 cos 6^f M ^{д к} 2 — к д T ¹ д Т ,                I д Т ²

MH [ 2 к , cos 2 6 + 12 к ₂ sin ² 6 cos ² 6— 4 к ₂ sin ⁴ 6 + MH cos ( T — 6 ) ]

^{— T} T M ^{cos (T—6)} , ^c h ^{д T}

— (5)

В последние годы МКЭ в магнитных веществах привлекает пристальное внимание исследователей и инженеров. Это эффективный и универсальный метод для изучения магнитных структур, обменных взаимодействий, магнитной анизотропии, магнитных фазовых переходов ит. д., для которого не требуется сложного экспериментального оборудования. На практике МКЭ может быть

где О и г - углы между направлениями намагниченности, внешнего магнитного поля и выделенной осью;

T п„ = С „ +    X

H 0 M 2

X

. ™Г,,д к , д M ] . . ₃„ Д,,д к , д M sin26 M —¹ — к  + 4sin ³ 6cos6 M —² — к,

_ д Т ¹ д Т J              I д Т ² д Т

д к ,

д Т

[2 к , cos 26 + 12 к ₂ sin ² 6cos ² 6 — 4 к ₂ sin ⁴ 6+ MH cos ( T —6 ) ]

здесь С0 - решеточная теплоемкость. По (6) следует, что теплоемкость кристалла в магнитном поле - существен

но анизотропная величина.

В отсутствие магнитной анизотропии (k_Y = k = 0) выражение (5) переходит в известное для изотропного ферромагнетика (1); а соотношения между М(Т), k₁(T), k₂(T) в (5) обеспечивают нагревание либо охлаждение образца.

Плотность свободной энергии кубического кристалла в магнитном поле может быть записана в виде .

22  22  22    222

f     f 0   I k i I 10* 1 ^a 2   I La 2 La 3   I *0* 3 La i     I k 2 La i La 2 ^* 3     I 1MH   . (/)

Аналогичным образом можно определить изоэнтро

пы МКЭ для ориентации магнитного поля в различных кристаллографических плоскостях. Для плоскостей (100),

(110), (111) они имеют вид

( A T 3    _ T _________ k 1 sin² 46 _________

I A H J j(100) c_H 4 MH [ 2 k 1 cos4 6 + MH cos 6 ]

f d k. , d M 3 T d M x M —¹ - k

( d T ¹ d T J c_H d T

cos ( ^-6 ) ,

T sin2 46         (dk cH _ cn +                       M —1

^{H 0} 4 M ² [ 2 k , cos 46 + MH cos 6 ] ( d T

f A T I A H

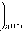
3cos ² 6+ - -

-------^—7------^^X f 3          1 3

MH { k i [cos26l 4 cos ² 6 + 4 1-

, d M 3

*»[«

-3 k sin ² 6 cos 60 + L sin ² 6 cos ² 6- ^- k, sin ⁴ 6 sin 26][sin 26 ^f 3cos ² 6+ ^- Y M — - k, M

2 ^{1                2}               4 2                     14        4 Yd T ¹ d T

X                 3,9,3                  ,                        ,

-4sin ² 26-4sin ² 26 + 4sin46] + k 2 [3sin 2 6cos46-3sin46cos 2 6-

-

3           f мдk  , d M 3             f „<дk  , d M 3

— sin ² 6cos6 M —¹ - k     + sin ³ 6cos ³ 6 M —¹ - k

2           Id T ¹ d T J              Id T   ¹ d T T d M , _nA

---------------¹-----------1-------------------¹-------------------T T ^cos (^ ^{- 6}),

-sin ³ 6sin 206cos6-2 sin ⁴ 6cos26] + MH cos(¥-6)}      c^H

T

⁺ M ²

{[sin 2 6^ 4 cos ² 6 + 4 3- 4 sin ² 6 sin 2 6 ] ( M d T - k - "d T 3+

{ k [2 cos2 6 ^f — cos ² 6 + — |— sin ² 2 6 — sin ² 2 6 + — sin4 6 ] + I 4        4 J 4         4         4

sin ³ 6 cos ³ 6- ^— sin ⁴ 6 sin2 6 Y M — - k M^-

4               JI    d T    ¹ d T

k 2 [3 sin ² 6 cos ⁴ ^- 3sin ⁴ 6 cos ² 6- sin ³

1;

6 sin2 6 cos 6- 2sin ⁴ 6 cos2 6 + MH cos ( Ф-6 ) ]

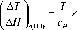
X---

MH

d k kM ^{2 2} I d T

-|sin2 6+ 144cos³ 6 sin 6- 1 296 cos⁵ 6

- 2cos 6- 432cos² 6 sin² 6 + 144cos⁴ 6 + 6480cos⁴ 6 sin² 6- 1 296 cos² 6

, (12) > I + MH cos ( ^-6 )

- - | M cos( T-6 ) c H ^d T

T

^:H = c ^{0 +} M

f M^k2-k2 ^M) f-3sin26 + 144cos3 6sin6-1296cos5 6] Id T d T j I 2                                                j x yi---------------u. (13) [k21 -2cos6-432cos2 6sin2 6 + 144cos4 6-6480cos4 6sin2 6-1 296cos‘ 6 ]+ MHcos(V-6)

В отсутствие магнитной анизотропии выражения (8), (10), (12) также переходят в известное для изотропного ферромагнетика выражение (1).

Формулы (5), (8), (10), (12) являются обобщением формулы (1) и позволяют описывать МКЭ на широком клас

се магнитоупорядоченных кристаллов.

Для иллюстрации рассмотрим МКЭ в поликристал-лическом образце. Макроскопическая изотропность поликристалла обеспечивает отсутствие вращающего момента во внешнем магнитном поле, так как среднее от вращающих моментов кристаллитов - векторных величин -равно нулю, но ситуация с МКЭ совершенно иная. При намагничивании поликристаллического ферромагнетика основной вклад в МКЭ по-прежнему дают про

цессы вращения намагниченности, поскольку в данном случае усредняется скалярная величина - работа намагничивания.

Продемонстрируем это на примере поликристалла с одноосными кристаллитами - аналога ГПУ- кобальта [8]. Для упрощения пренебрежем второй константой магнитной кристаллографической анизотропии и вкладом процессов вращения в теплоемкость. Поскольку оси кристаллитов изотропно распределены по объему образца, то угол с при достаточно сильном поле равномерно распределен от 0 до d / 2. В результате усреднения имеем

A T     2 T dk ,MM \ T dM _{л х}

= M - k . (14)

A H J j 3 c ₀ MH - dT ¹ dT ^J c dT

Здесь первое слагаемое также вносит существенный вклад в МКЭ.

Выражение (14) достаточно точно описывает знакопе-ременность эффекта при разных температурах и его коли

чественные характеристики для поликристаллического об-

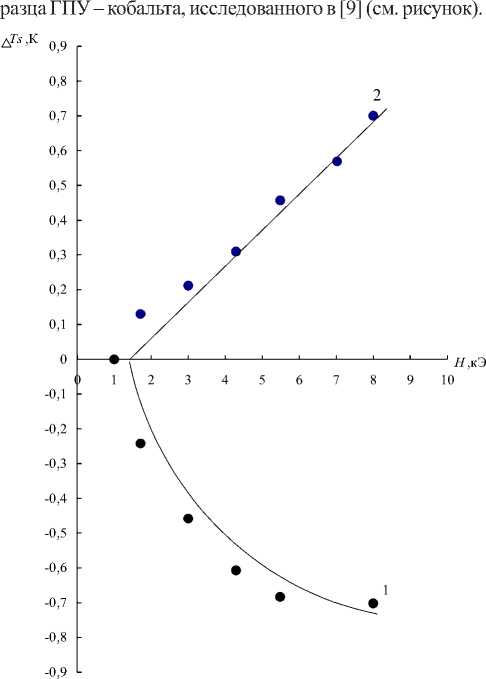
Магнитокалорический эффект в поликристаллическом образце ГПУ - кобальте при температурах: Т = 504 К (1),

Т = 612 К (2); точки - результаты эксперимента [9];

сплошные линии - результаты расчета по формуле (14)

Следует отметить весьма важное обстоятельство. Изоэнтропы (см.рисунок) показывают, что вклад процессов вращения растет с уменьшением напряженности магнитного поля. Нижний предел напряженности ограничен лишь возникновением доменной структуры. Следовательно, для практического использования МКЭ в данном случае не требуются сильные магнитные поля и связанные с ними большие энергозатраты. С другой стороны, в отли-

чие от намагниченности, константы магнитной анизот ропии магнитоупорядоченных кристаллов весьма чувствительны к наличию примесей, условиям термообработки и т д., что предоставляет широкие вазможности для выбора кристаллов, обладающих необходимым МКЭ.

Сильные эффекты следует искать в материалах со структурными фазовыми переходами [10], ориентационными фазовыми переходами [11] и в магнитных пленках с поверхностной анизотропией [12...14].

Новые типы магнитных холодильных машин. В последние годы обоснована перспективность создания новых типов холодильных машин, использующих МКЭ в ферромагнетиках [15...17]. Это прежде всего связано с достижениями в области физики твердого тела.

Один из типов магнитной холодильной машины предложен в [16; 17]. Ферромагнитное рабочее тело цикли чески перемещается между приемником и источником теплоты в неоднородном магнитном поле. В зоне сильного магнитного поля оно изотермически намагничивается, и выделенная теплота передается приемнику. В зоне слабого магнитного поля вследствие размагничивания тело охлаждается, и ему передается теплота от источника. В качестве рабочего тела был использован металлический гадолиний. МКЭ в гадолинии достигает 14 К при включении магнитного поля Н = 70 кЭ при температуре Кюри 293 К. Использование гадолиния в возвратно-поступательной машине обеспечило градиент температур 46 К.

Исследование вклада вращения намагниченности в МКЭ позволило сформулировать новый принцип магнитного охлаждения. Рассмотрим композиционный ферромагнетик, выполненный из пар блоков, имеющий намагниченности М₁и М₂ и константы одноосной анизотропии к₁ и к₂ разных знаков [18]. Можно показать, что вращающий момент такого композита во внешнем магнитном поле напряженностью Н имеет вид

L = ( kV + kV ) sm2 ^ + f kV + kV ) sin 4 ^ , (15) 11 22 MM H

V 1 2 у где ^ и V- суммарные объемы блоков; г - угол между напряженностью магнитного поля и одной из осей легкого намагничивания. Адиабатическое изменение температуры при повороте ферромагнетика в магнитном поле на угол ДГ

A T = - ^{T dL} дщ . (16) c _т dT

Очевидно, что полное изменение температуры AT за период вращения композиционного ферромагнетика в постоянном магнитном поле равно нулю. Однако если его вращение происходит в меняющемся по амплитуде магнитном поле, то AT может быть отличен от нуля. В частности, если напряженность магнитного поля меняется от Н₁ до Н₂ при вращении рабочего тела на угол d / 4, то полное изменение температуры за период будет

8 T = 2T х

2 kV д k 2 kV д Ь kV д M, k,’V д М₂ 11    1      22    2     1 1     1     2 2     2

---1---------

M 1 д T M ₂ д T M 1 д T M ₂ д T

^Х (17)

( 1

1 )

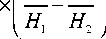
В зависимости от величин констант магнитной анизотропии, намагниченностей и их производных по

Гi i температуре, а также от знака разности

мож-

^^^^^^.

I 7^i 21₂ но получить нагревание илиохлаждениДтела.   ⁷

Сделаем оценки изменения температуры рабочего тела за период. Взяв типичные значения ^ ~ 10³ эрг / см³, . _ д k                    д M

М, ~ 10⁴Гс, —~ 10³ эрг/(см³ • К),--- = 10 ^{- 1} Гс/К,

• 1 -2          , дT          р (        ), дT

с ~ 10⁷ эрг / (см³ К), Н ~ 10³ Э, T ~ 10³ • К, имеем 8 T = 10 ^{- 2} К, что в данном магнитном поле по порядку величины соответствует магнитокалорическому эффекту, связанному с изменением магнитной части энтропии изотропного образца при намагничивании. Существенной особенностью этой холодильной машины является непрерывное охлаждение рабочего тела.

Таким образом, можно сделать следующие выводы:

• -    исследован магнитокалорический эффект в магнитоупорядоченных монокристаллах с учетом процессов вращения намагниченности;

• -    получено выражение для магнитокалорического эффекта в ферромагнитном поликристалле, хорошо описывающее экспериментальные результаты;

• -    предложен новый принцип работы магнитной холодильной машины, рабочим телом которой является композиционный ферромагнетик с взаимно перпендикулярными осями легкого намагничивания. Охлаждение рабочего тела реализуется при его вращении в синхронно изменяющемся по амплитуде внешнем магнитном поле.