Магнитооптические свойства дифракционной решётки на магнитной подложке

В настоящее время металлодиэлектрические структуры с резонансными свойствами являются предметом интенсивных исследований [1]. Большой интерес представляют гетероструктуры, содержащие намагниченные слои и обладающие резонансными магнитооптическими свойствами [2–4]. В работах [2–4] исследованы магнитооптические свойства двухслойной гетероструктуры, состоящей из металлической дифракционной решётки и диэлектрического намагниченного слоя (вектор намагниченности перпендикулярен слою). В [2–4] показано, что в указанные структуры обладают как резонансами пропускания, так и резонансами углов Фарадея и Керра.

В настоящей работе исследуется структура, состоящая из золотой дифракционной решётки на намагниченной подложке, вектор намагниченности направлен параллельно штрихам решётки. В результате численного моделирования на основе метода Фурье-мод обнаружено, что в данной структуре возникает нечётный по намагниченности магнитооптический эффект, заключающийся в изменении коэффициента отражения структура при изменении намагниченности подложки. Величина эффекта на порядок превышает аналогичные эффекты для однородных магнитных плёнок [5, 6].

ГЕОМЕТРИЯ СТРУКТУРЫ И ТИП

МАГНИТООПТИЧЕСКОГО ЭФФЕКТА

Геометрия исследуемой структуры представлена на рис. 1. Структура состоит из бинарной дифракционной решётки из золота, расположен-

Быков Дмитрий Александрович, техник.

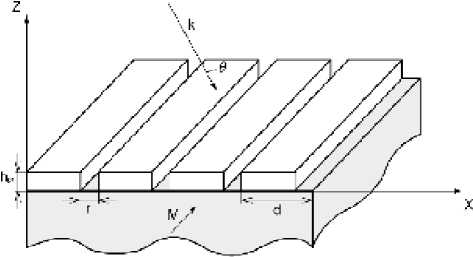
Рис. 1. Геометрия структуры

ной на подложке из намагниченного материала. Вектор намагниченности M направлен вдоль штрихов решётки.

Показатель преломления среды над структурой равен единице. Тензор диэлектрической проницаемости материала подложки имеет следующий вид [7]:

^£ M =

£

. - ig

0 ig

£ 0

0 £

где g — модуль вектора гирации среды, пропорциональный намагниченности [5]. Магнитная проницаемость всех материалов считается равной единице [7].

Для моделирования процесса дифракции света на рассмотренной структуре применялся метод Фурье-мод [8]. В расчётах была использована численно-устойчивая реализация метода, рассмотренная в [9, 10].

На риc. 2 представлены расчётные зависимости коэффициента отражения от длины волны для трёх значений намагниченности: - g , °, + g . Случай g = 0 соответствует нена-

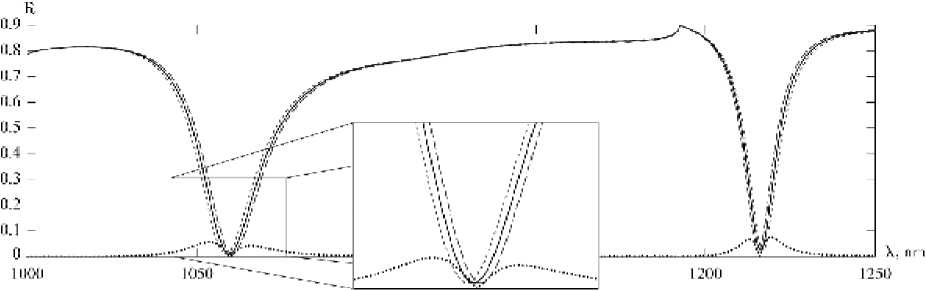
Рис. 2. Зависимость интенсивности нулевого отражённого порядка от длины волны при отсутствии намагниченности ( g =0 — непрерывная линия) и противоположных направлениях (“ + g ” — длинный пунктир, “ — g ” — короткий пунктир). Величина интенсивностного эффекта (2) — точечная линия

магниченной подложке, случаи “ — g ” и “ + g ” соответствуют двум противоположным направлениям вектора намагниченности. Расчёт проводился при наклонном падении волны с ТМ-поляризацией под углом 0 = 12 o при следующих параметрах: период d = 485 нм, ширина отверстия a = 0.05 ■ d = 24 нм , толщина решётки h_gr = 163 нм . Для диэлектрической проницаемости материала решётки использовались справочные данные для золота [11]. Для тензора диэлектрической проницаемости магнитного слоя использовались параметры е = 5.06 + 0.0004 / , g = (1.53 — 0.003 i ) х 10 ^{- 2} . Указанные параметры являются типичными для магнитооптических материалов типа вис-мут-замещённый диспрозиевый или иттриевый феррит-гранат в области ближнего ИК.

Рис. 2 показывает, что введение намагниченности приводит к смещению спектров, соответствующих случаям “ — g ” и “ + g ”. Определим величину интенсивностного эффекта в отражении по формуле

I r ( g )=| R » ( - g ) — R >( g ), (2) где R ₀ ( g ) — интенсивность нулевого отражённого порядка дифракции при намагниченности подложки “ + g ”. Величина интенсивностного эффекта показана на рис. 2 точечной линией. Максимальная величина эффекта близка к 8%. Следует отметить, что величина эффекта (2) для плёнок ферромагнитных материалов составляет всего порядка 0.1% [5]. В работе [6] исследован аналогичный интенсивностный эффект в многослойной системе магнитных плёнок. В [6] показано усиление интенсивностного эффекта при генерации в системе ПЭВ, однако величина эффекта также составляет менее процента. Таким образом, величина интенсивностного эффекта на рис. 2 является значительной по сравнению с аналогичными эффектами для намагниченных однородных плёнок.

ОБЪЯСНЕНИЕ

МАГНИТООПТИЧЕСКОГО ЭФФЕКТА

Согласно рис. 2, интенсивностный эффект наблюдается в окрестностях длин волн Л = 1060 нм и Л = 1220 нм . Отметим, что в разных минимумах спектра смещение происходит в разные стороны. Например, при длине волны Л = 1060 нм смещение минимума отражения при намагниченности “ + g ” происходит в сторону больших длин волн, а при длине волны и Л = 1220 нм — в сторону меньших.

Анализ распределения поля под решёткой показал, что рассматриваемые эффекты связаны с возбуждением поверхностной электромагнитной волны (ПЭВ) на нижней границе решётки. Действительно, длины волн Л = 1060нм и Л = 1220 нм хорошо совпадают с условием возбуждения ПЭВ на нижней границе дифракционной решётки порядками ±1. Условие возбуждение ПЭВ порядком с номером m имеет вид kx, m Re ( kspp ),

где к = +Z'

SPP 0

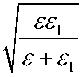
— константа распространения ПЭВ для границы раздела сред между металлом (диэлектрическая проницаемость Е1) и ненамагниченным диэлектриком (диэлектрическая проницаемость Е ). Из (4) получим длину волны в виде d Re k^pp

^Л т =-- T PP - Sin ⁰

m (  k0         )

Из (5) при m = ± 1 получим Л _{— 1} = 1056 нм и Л _{+ 1} = 1226нм , соответственно. Таким образом, минимумы отражения на рис. 1 при g = 0 хорошо совпадают с условием возбуждения ПЭВ.

Смещения спектров при значениях намагниченности ± g связаны с зависимостью условия возбуждения ПЭВ от величины намагниченности. Константа распространения ПЭВ на границе раздела между металлом и магнитной средой с тензором диэлектрической проницаемости (1) может быть получена из уравнений Максвелла в виде:

s г kspp (g) = kspp (0) —ik0g",------"^T,------7 + o(gX (6)

( s + s j ( s — s j       ^{v 7}

где первое слагаемое — константа распространения ПЭВ для границы двух ненамагниченных сред. В (6) в качестве в качестве s, g следует использовать вышеприведенные компоненты тензора (1) диэлектрической проницаемости подложки. Согласно (6), при малых g зависимость константы распространения ПЭВ от намагниченности g является линейной. Уравнение (6) позволяет получить длины волн, при которых происходит возбуждение ПЭВ при намагниченной подложке в виде d           s2

Am ( g ) = Am ( 0 ) + — Im g 7-----Тз/Ъ-----7 ’ (7)

m    ( s + ej ( s- 5) ⁽⁾

где A m ( 0 ) имеет вид (5). Формула (7) объясняет смещение минимумов отражения по длине волны на рис. 2. Согласно (7), смещение минимумов, соответствующих порядкам с номерами + 1 и _— 1 , должно происходить в разных направлениях, что также наблюдается на рис. 2. Формула (7) также позволяет оценить величину смещения минимумов спектров на рис. 2. Для первых порядков получим следующие величины смещений AA_{— 1} =j A_{— 1} ( g ) — A_{— 1} ( — g )| = 2.2 нм , AA_{+ 1} = A _{+ 1} ( g ) — A_{+ 1} ( — g ) = 1.7 нм . Расчётные значения согласуются с расстояниями между минимумами спектров при намагниченностях “ + g ” и “ — g ”. При A = 1060 нм и A = 1220 нм расстояния между минимумами смещенных спектров на рис. 2 составляют 2 нм и 1.4 нм, соответственно.

При малых g не только константа распространения ПЭВ, но и величина наблюдаемого эффекта (2) линейно зависит от g. На рис. 3 приведена расчётная зависимость величины интен-сивностного эффекта от g при A = 1065 нм . Значения по оси абсцисс нормированы на величину Re ( g ) = 0.0153 , использованную при расчёте спектров на рис. 2. Рис. 3 показывает близкий к линейному вид эффекта по g .

ЗАКЛЮЧЕНИЕ

Структура, состоящая из золотой решётки на диэлектрической подложке, намагниченной параллельно штрихам решётки, обладает нечётным

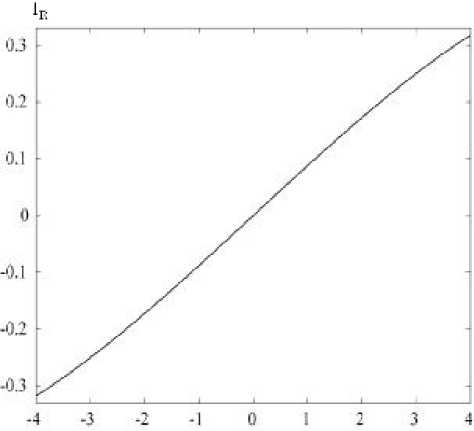
Рис. 3. Величина интенсивностного эффекта в зависимости от g по намагниченности интенсивностным эффектом. Эффект объясняется зависимостью условий возбуждения ПЭВ волн на нижней границе решётки от величины намагниченности материала подложки. Изменение условий возбуждения ПЭВ вызывает смещение минимумов в спектре пропускания при изменении намагниченности. Рассмотренные гетероструктуры могут быть использованы в оптических датчиках магнитного поля.

Работа выполнена при поддержке грантов РФФИ № 09-07-92421, 08-07-99005, 07-01-96602, 07-07-91580, гранта Президента РФ № НШ-3086.2008.9, “Фонда содействия отечественной науке”, фонда “Фундаментальные исследования и высшее образование” (RUXO-014-SA-06).