Максимально правдоподобные оценки параметров оптических сигналов с учетом дробового и фонового шумов

В отличие от приема сигналов радиосвязи и радиолокации, когда шумы и помехи можно считать независимыми, детектирование оптических сигналов сопровождается неустранимым дробовым шумом, статистические характеристики которого тесно связаны со значениями самого сигнала. Эта особенность не позволяет напрямую использовать весь имеющийся в наличии богатый арсенал методов и средств оптимального приема и требует разработки специальных методов и алгоритмов оценивания, учитывающих взаимную зависимость между сигналом и сопровождающим его шумом. Ситуация усугубляется еще и тем, что приему мешает фоновая засветка фотодетектора и его тепловой шум. Эти помехи также должны быть учтены при разработке методов оптимального приема.

Первая монография, посвященная решению задачи оптимального приема оптических сигналов, появилась еще в 1967ом году [1], однако, в силу несовершенства источников света и фотодетекторов того времени, их шумы существенно превосходили дробовой шум сигнала, и алгоритмы оптимальных оценок строились без учета зависимости сигнала и шума. С появлением лазеров и фотодетекторов – счетчиков фотонов, шумы источника и детектора резко уменьшились, и основной помехой стал дробовой шум. Теперь уже специалисты в области приема оптических сигналов учитывают эту ситуацию, но сосредоточились пока на задачах обнаружения, минимизации отношения шум – сигнал и оптимальной линейной фильтрации [2-6]. В то же время развитие методов оптимального оценивания, учитывающих связь сигнала и дробового шума, несомненно будет содействовать существенному улучшению надежности оптической связи, достоверности работы устройств дисковой оптической памяти, повысит точность лазерных локационных систем и оптико-электронных измерительных устройств в научном эксперименте, промышленности и медицине. Наряду с [7-9], наша работа является попыткой на частном примере оптического импульса заданной формы показать пути решения этой задачи.

В большинстве случаев приема оптических сигналов априорные сведения о распределении их параметров отсутствуют, в то время, как статистика сопровождающего дробового шума и ее связь со значениями сигнала хорошо известны: дисперсия дробового шума в каждой точке оси времени пропорциональна интенсивности сигнала в той же точке. В этой ситуации, как известно, [10,11], наиболее эффективным критерием оптимальной оценки параметров сигналов является достижение максимума функции правдоподобия. Именно этот путь будет использоваться нами в данной работе. Далее в соответствии с теорией фотоэффекта [12-15] примем, что поток первичных фотоэлектронов и, соответственно, поток одноэлектронных импульсов на выходе фотоумножителя или лавинного фотодиода подчиняется распределению Пуассона. Что касается статистики, первичных электронов, то при приеме когерентного излучения эта модель адекватна реальности. Если же принимается тепловое излучение, то при условии, что длительность времени измерения превышает время когерентности, соответствующее этому случаю биномиальное распределение фотоотсчетов с отрицательным показателем также переходит [16] в Пуассоновское. Для реальных условий, когда длительность сигнальных импульсов превышает 10 наносекунд (длительность измерений соответственно 1 наносекунда), это условие хорошо выполняется. Так, например, если ширина спектра теплового фонового излучения при длине волны λ =10 мкм равна 10нм, то время когерентности τ k = λ ²\ ∆λ C (где С – скорость света) составляет всего лишь 0,033 нсек, т.е. оно много меньше длительности отсчета. Реальные фотодетекторы из-за сложности явлений размножения фотоэлектронов, конечно искажают исходные распределения фотоэлектронов [17-19], и, в этом плане, выбранную нами Пуассоновскую модель следует рассматривать, как первое приближение.

И еще одно замечание относительно фонового и теплового излучения: изменение его интенсивности во времени происходит существенно медленнее, чем изменение формы большинства используемых на практике сигналов. Поэтому значения интенсивно- сти фона и соответствующего им дробового шума могут быть заранее оценены. C учетом этого, в дальнейшем мы полагаем, что интенсивность фонового излучения и среднего значения темнового тока известны и являются постоянной величиной.

Существуют три основных способа фотодетектирования оптических сигналов:

• 1.    Счет числа фотоэлектронов на интервале ∆ t равномерно квантового сигнала по времени;

• 2.    Б. Фиксация момента эмиссии каждого фотоэлектрона;

• 3.    Аналоговое фотодетектирование, когда поток фотоэлектронов сглаживается инерционность фотодетектора.

Метод подсчета числа фотоэлектронов хорошо согласуется с возможностями современной электронной техники и позволяет достаточно простыми средствами преобразовать интенсивность оптического сигнала в цифровую форму. Учитывая это, задачу оптимальных оценок будем решать, ориентируясь именно на этот метод. Упрощенная функциональная схема оптимального дискретного фотоприема показана на рис.1:

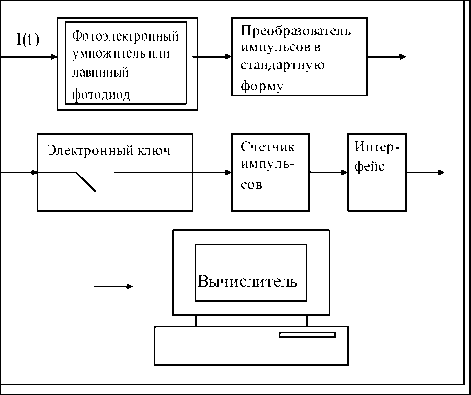
Рис.1. Схема оптимального дискретного фотоприема

График входного оптического импульса (верхний график) и одной из возможных реализаций выходного цифрового сигнала (нижний график) представлены на Рис.2.

Здесь под дробовым шумом мы понимаем отклонения значений выходного сигнала от значений оптического сигнала с учетом, конечно, соответствующего масштабного коэффициента κ/hν. С учетом этих особенностей дискретного фотоприема, задача оптимального оценивания параметров оптических сигналов решается на основе получаемой цифровой последовательности значений выходного сигнала, состоящего из аддитивной комбинации двух составляющих, одна из которых пропорциональна оптическому сигналу, а вторая – случайная – является дробовым шумом, рожденным самим этим сигналом. Что касается влияния интенсивности фона, то оно учитывается как случайная составляющая, рожденная этим фоном.

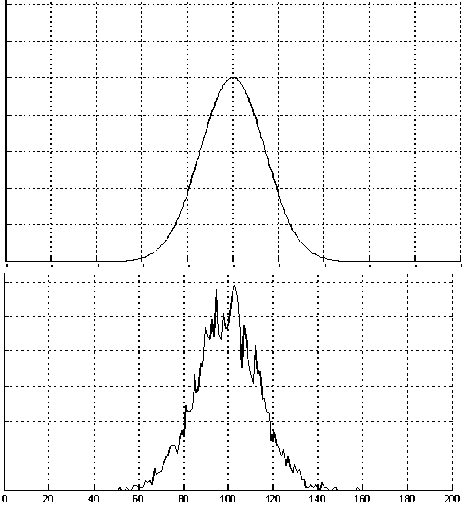
Рис. 2. Графики оптического импульса и выходного цифрового сигнала

В начале статьи на основе принятой модели представлен вывод обобщенного уравнения правдоподобия для любой формы сигнала и фонового излучения. Затем, в разделе 2 на примере приема оптического сигнала гауссовой формы в отсутствии фонового излучения получена система уравнений правдоподобия и найдены их аналитические решения для всех трех неизвестных параметров импульса: амплитуды А, длительности τ и положения на оси времени t 0 . В разделе 3 на основе уравнений правдоподобия в явном виде получены выражения для границ Рао-Крамера, определяющие качество получаемых оценок в виде минимально возможных дисперсий. В разделе 4 на примере оценки амплитуды гауссова импульса продемонстрирован путь численного решения уравнения правдоподобия с учетом фонового излучения. В этом же разделе с целью подтверждения возможности реализации этого пути и оценки качества получаемых оценок, представлены результаты модельного эксперимента, когда на основе заданных параметров сигнала и фона вычислялась модель соответствующего электрического сигнала, и затем на ее основе находилось решение соответствующего уравнения, а также мат. ожидание и дисперсия полученных оценок.

В присутствии фонового излучения не допустимы слишком большие времена измерений, так как со временем значение сигнала падает, а дробовой шум фона не исчезает. С учетом этого определена оптимальная длительность процесса измерений.

Уравнение правдоподобия при дискретном фотодетектировании

Пусть на катод счетчика фотоэлектронов поступает оптический сигнал интенсивностью I c (t) и фоновое излучение с интенсивностью I ф (t) , тогда, как известно из теории фотоэффекта [13-16] с выхода детектора пойдет поток фотоэлектронных импульсов со скоростью

скобках при малом в сравнении с длительностью сигнала интервалом квантования A t может быть заменен интегралом в бесконечных пределах. Тогда уравнение правдоподобия (6) преобразуется к окончательному виду:

N   nA (tj

2 Ac (tj + Хф (tj

to

— J A ' ( t i ) dt = 0 .

—to

X (t) = Х _с(1)+ Х ф (1) = ^Mn,<+ ^t) ! , h v h v

где к - квантовая эффективность фотокатода, а h v - энергия кванта света. Если известен темновой ток фотодетектора, то он также может быть учтен путем соответствующей коррекции значений фонового излучения.

В соответствии с принятой нами моделью, поток фотоэлектронов, определяемый (1), подчиняется распределению Пуассона. Это значит, что вероятность насчитать n фотоэлектронов на интервалах квантования A t в близи точки t i определяется как:

P⁽n. , t i ) = ^A ( t i ) ^A t ] exp ^{( — A (} t i ^{) A} t ) .                   (2)

ⁿi ^!

Совместная вероятность насчета n i фотоэлектронов на интервале A t в точках t₁^t_i^t_N (функция правдоподобия), в силу статистической независимости пуассоновских отсчетов будет определяться следующим произведением:

N

P(n i ^n N , t l ^t N ) = П P ( n i t i ) ,                  (3)

i = 1

где N – кол-во отсчетов на интервале наблюдения (оценки параметров) сигнала. Чтобы получить уравнение правдоподобия, необходимо найти логарифм функции правдоподобия, продифференцировать его по оцениваемому параметру и приравнять полученное выражение к нулю. Логарифмируя и дифференцируя (3) с учетом (2), получим:

N

= 2 [ n i (ln A ( t, ) - In A t ) - In n i ! — A ( t, ) A t ] ,              (4)

i = 1

Решив это уравнение при заданной форме сигнала A _c(t, x) , фона А _ф() и полученной реализации отсчетов n(t i ) относительно неизвестного параметра х , можно найти его максимально правдоподобную оценку с минимальной дисперсией. Если число оцениваемых параметров равно k, то, составляя и решая систему из k уравнений вида (7), получим оптимальные по точности оценки всех k параметров.

Решение задачи оптимальных оценок проведем на примере сигналов гауссовой формы

^f ( t — 1 ₀ ) ²)

I (t) = I о exp|--2— I, l т )

где I 0 – амплитуда интенсивности оптического сигнала. В соответствии с (1), скорость эмиссии фотоэлектронов A _c(t) примет вид:

A ( t ) = A exp | — ——20)— | , l т )

Здесь a = I0^ - скорость эмиссии фотоэлектро-hv нов (скорость счета) в точке t0.

Эта форма принята нами, как одна из реальных применяющихся на практике. Например, гауссова форма оптического сигнала имеет место при рассеянии света малой частицей пересекающей лазерный пучок, гауссовы импульса применяются также в световолоконной связи и устройствах оптической дисковой памяти (CD, DVD, МОП).

Оптимальные совместные оценки параметров оптических сигналов на примере гауссова импульса в отсутствии фонового излучения

Рассмотрим в начале случай, когда фоновое излучение и темновой ток пренебрежимо малы. Тогда уравнение (7) принимает вид:

dx

N

=2

i = 1

ⁿi ^ '⁽ t i ) . A ( t i )

^{— A} '⁽ ti ^{) A} t

N i=1

n i A '( t i ) . Ac ( t i ) _

to

— J A '( t i ) dt = 0.

—to

где A' (t_i)=d A (t_i)/dx , а х - оцениваемый параметр.

Тогда, с учетом (1.1) и (1.5), уравнение правдоподобия запишется в следующем виде:

N i=1

n i ^{A (}t i ) A c ( t i ) + А ф ( t i )

— A ( t i ) A t

= 0.

Подставляя в (10) соответствующие частные производные A (t, A, т , t₀) по A, т , и t₀ , получим следующую систему уравнений правдоподобия для оценки параметров A, т , t₀:

1 ^N

—2 ni = Птт,

A1= 1

Если, как это обычно бывает, весь сигнал умещается на интервале наблюдения, то второй член (6) в

N

2 ni(ti— t 0)2 = i=1

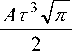
N

E ^п. ⁽ ч - t 0 ) = ⁰

i = 1

Решая эту систему уравнений, находим:

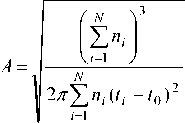
N nt i=1

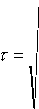
N

² E n i ⁽ t i - t 0^{) 2}

i =1 ____________________

N

E ni i =1

статистическое осреднение. Производная логарифма функции правдоподобия по оцениваемому параметру была выведена ранее (5), и, если весь сигнал, как это обычно бывает, умещается на интервале наблюдения, может быть представлена в виде:

d in L ( x ) dx

f n ^ X t i ) ^E Я ( ti)

to

- J я х t ) dt

-to

t 0 =

N

E ni i =1

Подставляя оценку t ₀ из (12) в выражения для

A и Т , получим окончательно:

A =

( Л I ²

I У n I

I ⁱ I

V i = 1    7

NN

2п Е n i E n i t} i = 1 i = 1

■ Л X ²

У nt, I ii

, i = 1        7

,

= ^. я х t i ) - C

^E я ( t i )       x ’

to где Cx = J яхt)dt, а ЯХt) - производная от Я(t) по

-to

оцениваемому параметру.

С учетом (5) и (17) элемент J mn матрицы Фишера примет вид

NN

J mn = М = ( EE i = 1 j = 1

nin j ^' m ⁽ ti) ' ^Я'п ⁽ t j ) Я ( t .) ■ Я ( t j )

— C m E j = 1

j'n ⁽ t j ) ^я ( t j)

N

- C n E j = 1

n i^'m ⁽ t i ) , C C Я ( t i ) ^{m    11}

где ^ m и ^ n - производные от Я (t) по соответствующему оцениваемому параметру, а C m , C n , в

NN

Т = _aE n E n^

E n> 1 ⁱ = ¹

i = 1

t 0 =

N

E niti i=1

N

E n i =1

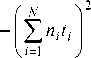
Таким образом, имея набор измеренных значений n i числа фотоэлектронов на каждом из интервалов Jt в моменты t i , можно, пользуясь выражениями (13)-(15), найти максимально правдоподобные оценки каждого из трех неизвестных параметров оптического импульсного сигнала.

Теперь осталось определить качество этих оценок.

зависимости от положения элемента J _mn в матрице

Фишера, принимает следующие значения:

C A ■ ( Я . ( t ) dt = to expf-I dt = T

^:                  J                  _T²      I

• -to            -to V              7

to                  9 Д to

C T = J Я Т ( t ) dt = - J ( t - 1 0 )² X

• -to                  ^T -to

x exp-- 0t — I dt = - 4пЛ             ⁽¹⁹⁾

V ^T 7

to             2Л to

C t 0 = J A t0 (t ) dt = — J( t - 1 0 ) x

-to              T -to f (t - to)2 Ъ x expl--0— 1 dt =

V T )

Границы Рао-Крамера для совместных оценок параметров гауссова импульса

Как известно [10-12], качество максимальноправдоподобных оценок параметров сигналов определяется границами Рао-Крамера. Минимальные дисперсии для каждого из оцениваемых параметров равны диагональным элементам корреляционной матрицы ошибок, которая обратна матрице Фишера. Элементы матрицы Фишера имеют вид [10]:

J mn = mHn>,                           (16)

где H= Е. [in l(x)]. Здесь х - оцениваемый параметр, dx а L(x) - его функция правдоподобия, < > - означает

Статистическое осреднение в (18) выполнено в Приложении, где показано, что

N

J =У mn i=1

я ; ( t i ) ■ я 2 я ² ( t i )

⁽ t j )

---+

NN

+ EE

(n^ln j ^x t< t i ) ■ ^я 2 ⁽ t j )

Я ( t i ) ■ я ( t j)

C ^ knjV’" ⁽ t j) m^Th Я( t j)

^л ( n i Я m ( t i ) C n E

Я ( t i )

+ С c

⁺ mm n^n .

Основываясь на (20), найдем элемент матрицы Фишера J_Aт. Учитывая (11) и переходя в (20) от сумм к интегралам, получаем выражение для суммы первых двух членов (20) в виде:

J A т 1 + J Лт 2

N

= 2

i = 1

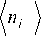
2 1 ( t i ) • 2 2 ( t j ) ⁺

24 t i )

Исходя из (21)-(24), получаем, что

JAt 0 = ⁰.                                           ⁽³²⁾

Найдем теперь элемент J _{T t0} . Действуя аналогично предыдущему, т.е. переходя к интегралам в (20), получим следующие значения всех пяти его членов:

NN

+ 22

i = 1 j = 1

П n^ ^ t i ) • 2 2 ( t j ) 2 ( t i ) • 2 ( t j )

- V n - n A т

Третий, четвертый и пятый члены (20), с учетом (19) соответственно будут равны:

N J лт 3 = C x i 2- i = 1	\ nt ^ 2 ( ti ) = 2 ( t i )	- л Л т ,	(22)
N JAT 4 = Cx, 2- i = 1	(nx ( ti ) = 2 ( t i )	-Пт ,	(23)
I . = C C u ArS xixixjxj	= - л Л т .		(24)

При этом учтено, что

4 A Jn 01 + J« 02 =        , т	(33)
Jt 03 = 0,	(34)
Jt 04 = 0,	(35)
Jt 05 = 0 .	(36)
Таким образом, 4 A J n 0 =     . т	(37)

Действуя аналогично, с учетом того, что по определению J_mm = /( H m )² \ , получим диагональные

элементы матрицы Фишера J_AA , J _тт и J_t0t0 :

(  - _t_ 'i² 1

(n^ = A exp - -!—--- At, l т )

^JAA =

Пn j ^ = A exp

-

( t j

-

t ₀)

2 1

l

т

^A t ,

J tt

так как А t<< т ...

Подставляя (20)-(23) в (20), получим окончательное выражение для элемента J_{А т} матрицы Фишера в виде:

^J A t =

п .

Теперь найдем элементы матрицы Фишера, касающиеся параметра t0.

Сначала найдем элемент J At0 . Учитывая выражения (19) и переходя в (20) к интегралам, первые два слагаемых (20) получим в виде:

9 ^to ( /2 1 2 t

^J At 01 ^{+ J} At 02 = J t ^exPl2" I ^{dt + т} -to l ^т )

Л ”      ( t 2 to

2 A          t

+ — J exp l -I dt • J t ^т -то l ^т ) -to

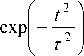
Учитывая (19), третий член (20) будет равен:

I          N ⁿ i ^{2 (} t i ) = 0

J At 03    C xm 2^     i/* \ ^O.

i = 1      ^{2 (} t i )

Аналогично четвертый и пятый члены в (20) будут равны:

«Ui \X'_m ( ti )

J At 04 = ^cx „ 2 ^x i ™    = 0,                 (30)

i = 1      ^{2 (} t i )

J At 05 = C A ' Ct 0 = ^{х Пт} • ⁰ = ⁰ .                  ⁽³ 1)

( d In L ( A ) 1 \

\ l dA )

l \                   / )

^{- 1}

/( d ln L(т) 1\

\ l   dT) / l \/ )

^Jt 0 1 0 =

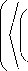
d ln L ( t 0 ) dt ₀

- 2

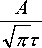
т

3 -JnA

- 1

т

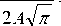
Таким образом, найдены все элементы матрицы Фишера. Инвертируя эту матрицу, получим корреляционную матрицу ошибок:

	А	T	t 0
А	A (3 n - 2)	n	1
	2 л/ пт ( n - 1)	2( n - 1)	2( n - 1)
T	П	тП	т
	2( n - 1)	2 A( n - 1)	2 A ( n - 1)
t 0	1	т	тП
	2( n - 1)	2 A ( n - 1)	2 A ( п - 1)

Ее диагональные элементы представляют собой дисперсии оптимальных оценок соответственно амплитуды А , длительности т и положения сигнала на оси времени t₀ , а недиагональные – коэффициенты корреляции соответствующих оценок.

Исходя из этого, можно записать следующие выражения для минимальных относительных среднеквадратичных ошибок оптимальных оценок:

£ L A

(3 п - 2)

2 A ПттП- - 1)

C

т

2 А т ( п - 1)

C 0

t ₀

тп

2 At 2 ( п - 1)

Если, например, А=10 9 эл/сек, т =10^-6 сек, то

^ A - =3,127%, — =2,03%, если 1 _о=10^-2 сек, то

А             т

^C t 0 =0,203%. t ₀

Оценка амплитуды оптического сигнала в присутствии фонового и дробового шумов на примере гауссова импульса

В случае присутствия как фонового, так и дробового шумов, оптический сигнал представляется в виде:

X (t i )= X c+д (t i ) At + X ф (t i ) A t,

где Л = A exp f- ( t ^t ⁰) ^с l       т т

,

Л _ф - скорость счета фо-

нового излучения.

Таким образом, уравнение (7) сохраняет свой вид:

Z   nA tf)

^Z А _с ( t , ) + Л ф ( t , )

T

- 2 J Л ( t ) dt = 0 .

При приеме Гауссова импульса уравнение (43) примет вид:

N

Z i=1

n i exp l

( t t 0 ) 2 ¹

т ² J

A expl

⁽ t ^- t 0^{) 2}

т

^{+ л} ф ⁽ t )

- J expl

- t ¹

l t ^% I d, = 0 т )

но n i =n CДi +n Фi , где n CДi – отсчет сигнала с учетом дробового шума, n Фi – отсчет фона.

К сожалению, найти его аналитическое решение не удалось, но, с учетом возможностей современных компьютеров, эта задача, по крайней мере, для одного неизвестного параметра, легко решается численными методами, например путем последовательного деления отрезка его возможных значений пополам. Это значит, что, получив реализацию выходного сигнала фотодетектора, мы, исходя из априорных сведений, задаемся интервалом возможных значений оцениваемого параметра. Затем делим интервал пополам и, подставляя крайние значения параметров в уравнение правдоподобия, находим значения невязок. Меньшее значение указывает, на каком подинтервале находится решение. Далее выбираем этот подинтервал и снова повторяем ту же процедуру. Повторение продолжается до тех пор, пока нас

устроит получаемый размер подинтервала, определяющий приемлемую ошибку данной частной оценки. Полученное при этом последнее значение подинтервала принимается в качестве окончательной оценки.

Чтобы определить возможную длительность такой процедуры оценивания при проведении вычислений с помощью современного персонального компьютера и оценить качество получаемых решений, мы провели модельный эксперимент с оценкой одного не известного параметра – амплитуды А. Его результаты приведены ниже. Суть эксперимента состоит в выполнении следующих шагов:

• 1)    Для заданного значения искомого параметра А, остальных известных параметров и известной постоянной интенсивности фонового излучения и темнового тока, строится модель электрического сигнала.

• 2)    Полученные значения сигнала подставляются в уравнение правдоподобия (2.7), которое решается описанным выше методом деления отрезка. Таким образом, находится оценка неизвестного параметра.

• 3)    Процедура моделирования сигнала и решения уравнения правдоподобия повторяется достаточно большое количество раз, например 100.

• 4)    На основе полученных результатов вычисляется выборочное мат. ожидание, дисперсия и среднеквадратичное отклонение полученной оценки, что позволяет оценить её качество.

Эксперимент проводился для значения амплитуды А=100 эл/сек, длительности импульса т =10 сек, значений t 0 =0 при интенсивности отсчетов фона 10, 30, 50 и 80 эл/сек. Полная длительность интервала наблюдения составляла Т=10 т , интервал квантования составлял 10^-2 т , а исходный диапазон выбранных значений амплитуды был выбран равным 200 эл/сек.

За основу программы моделирования были взяты процедуры библиотеки Mаtlab нахождения случайных величин с Пуассоновским распределением по заданному значению его параметра, и программа вычисления интегралов.

Следует учесть, что в присутствии фона недопустимо использовать слишком большие в сравнении с т длительности времени измерения Т, поскольку интенсивность фона практически не меняется во времени, а энергия сигнала сосредоточена на конечном интервале в близи значения t₀ ±T . Поэтому, чтобы найти оптимальные значения интервала Т, эксперимент был поставлен при различных длительностях сигнала в диапазоне от 0,1 до 50 т .

Опыт получения оценок показал, что современный компьютер решает задачу оптимальной оценки амплитуды в считанные секунды.

Чтобы оценить качество полученных оценок амплитуды, были найдены 100 оценок, их мат. ожидание, дисперсия и относительное среднеквадратичное отклонение. Результаты этого эксперимента сведены в таблицу при λ ф =10,30,50 и 80 эл/сек.

Таблица 1

T ( λ ф =10)	Мат. ожидание	σ A 2	σ /A
1	99.7139	0.2313	0.0048
5	99.8754	0.1038	0.0032
10	99.7489	0.0983	0.0031
20	99.7893	0.1149	0.0034
50	99.5812	0.1752	0.0042

Таблица 2

T ( λ ф =30)	Мат. ожидание	σ A 2	σ /A
1	99.5062	0.4137	0.0064
5	99.7753	0.7681	0.0042
10	99.6143	0.1578	0.0039
20	99.8559	0.1958	0.0044
50	100.2752	0.3027	0.0055

Таблица 3

T ( λ ф =50)	Мат. ожидание	σ A 2	σ /A
1	99.3867	0.4532	0.0067
5	99.7284	0.2395	0.0049
10	99.4623	0.2081	0.0045
20	99.9119	0.2377	0.0049
50	100.0675	0.3972	0.0063

Таблица 4

T ( λ ф =80)	Мат. ожидание	σ A 2	σ /A
1	99.4717	0.6242	0.0079
5	99.4848	0.2956	0.0054
10	99.9517	0.2538	0.0050
20	99.7817	0.3129	0.0056
50	99.9649	0.4916	0.0070

Сравнивая значения оценок А с истинной амплитудой видим, что разница даже при λ ф =50 эл/сек составляет всего 0,06%. Это означает, что мат. ожидание оценки амплитуды практически не смещено.

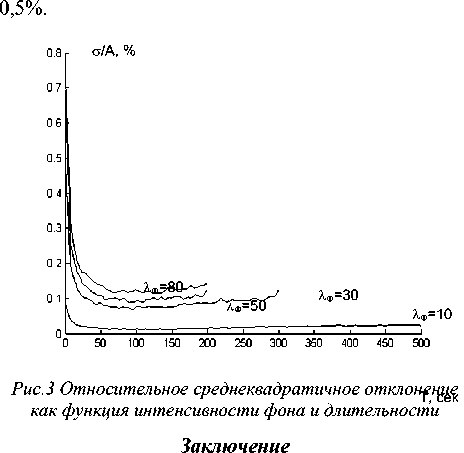
Относительное среднеквадратичное отклонение как функция интенсивности фона и длительности измерения представлена графиками на рис.3

Из этого графика следует, что ошибка в оценке имеет минимум по параметру Т. Причем, с повышением интенсивности фона, минимум ошибки сдвигается в сторону меньших Т, хотя следует отметить, что все значения Т min находятся вблизи значений τ . Таким образом, для получения оптимальных по точности оценок амплитуды гауссова импульса в присутствии фонового излучения, необходимо время измерения выбирать вблизи значений τ .

Если пользоваться этим алгоритмом, то можно утверждать, что относительное среднеквадратичное отклонение оценки для λф=10% от значения амплитуды не превышает 0,31%, а для λф=80% составляет

В общем виде получено уравнение правдоподобия для оптимального приема оптических сигналов фотоприемником – счетчиком фотонов с учетом дробового шума сигнала, фоновой засветки и темнового тока. На примере гауссова импульса в отсутствии фонового излучения и темнового тока найдены решения этого уравнения, позволяющие, располагая набором значений числа фотоэлектронов на каждом интервале равномерно квантованного сигнала легко вычислить совместные оптимальные оценки амплитуды, длительности и положения гауссова импульса на оси времени. Определены также элементы информационной матрицы Фишера, корреляционной матрицы ошибок и границы Рао-Крамера, характеризующие минимальные дисперсии этих оценок. Таким образом, разработчики лазерных систем связи, устройств оптической дисковой памяти и оптоэлектронной аппаратуры для научных исследований получают возможность сравнить полученные ими оценки с оптимальными и определить степень совершенства своих разработок, а специалисты в области лазерной локации могут воспользоваться алгоритмами оптимальных оценок.

Приложение.

Вывод обобщенного выражения элемента J mn матрицы Фишера

Как следует из (4.3), элемент матрицы Фишера имеет вид:

^{N N} n_i λ _m ′ ( t_i ) ⋅ λ _n ′ ( t_j ) J_mn = H_mH_n = ∑∑

-

λ ( t i ) ⋅ λ ( t j )

-

_C N n j λ n ′ ( t j ) ^{m ∑} j = 1 λ ( t j )

-

n_i λ _m ′ ( t_i )

Cn∑       +Cm⋅Cn j =1 λ(ti)

(П.1)

Так как среднее суммы равно сумме среднего, получим:

NN ∑∑ i = 1 j = 1

(n_i}(n_j\1'_х ( t )-X' ( t )

\ i I \ j / X1 x I 7 x2 x j 7

NN

J mn = ∑∑ i = 1 j = 1

( n i n j^'m ⁽ t iY^n ⁽ t j )

X( t , )-2( t j )

²( t , . )-2( t j ) i ≠ j

N (п \ X ‘ (

_- jn m k  X t j )

(П.2)

NN = ∑∑ i = 1 j = 1

( ⁿiXⁿX ^X' x 1 ⁽ ti^ '^ x 2 ⁽ t j )

X( t i )-2( t j )

N t n,- 2 ( ti ) i mi

Cn Z

i = 1

2 ( t i )

-

+ С С

⁺ mm ^п

Рассмотрим каждый член выражения (П.2) в от

дельности.

Первый член (П.2) равен:

J mn1

NN

= ZZ

, = i j = i

^{п n}iⁿj Х⁽ t i ) • ² X ₂ ⁽ t j ) 2 ( t i ) • 2 ( t j )

(П.3)

Пуассоновские случайные величины не коррели-

рованны, поэтому in j >=i>j> при i*j и inj>=1 > при i=j. С учетом этого,

N к 2 2 (^ ) • 2‘ (tz- ) i xi xi

т = V ' ' 1         2

^и mn1 Zi

i = 1

22( ti)

+

N ( n i /^C t D'X₂( t i )

^         X²( t i )

(П.8)

Докажем справедливость такого представления на примере, когда N=2. Первый член правой части (П.8) в этом случае можно представить в виде:

[1>f(t1)+2>f(t2)] [1>f(t1)+2>f(t2)]= =1>²f²(t1)+ 1>2>f(t1) f(t2) +

+ i>2>f(ti) f(t2)+ <п'\ПИ2                (П.9)

2                          2 2

= Z < ⁿi > ^{2 f 2(} t i ) ⁺ZZ < ⁿi > <  ⁿj > ^{f (} ti ) ^{f (} t j )

i = 1                              i = 1 j = 1

i * j

Где f ( t ,) = 2 ( t L ) 2 i < t i>

2 ² ( 1 1 )

Как следует из (П.9),

,

2 ; ( 1 1 ) 2 2 ( 1 2 ) ^{f (} t ^{2 )} = ^?o;r

.

NN zz может быть пред- i=1 j=1

i * j

NN

+ ZZ

i = 1 j = 1

(ⁿiXⁿ jV^l■ ) ) • ² X ⁽ t j ) 2 ( t i ) • 2 ( t j )

(П.5)

ставлена разностью (П.8).

Теперь, подставляя (П.8) в (П.7), получим

Для пуассоновских случайных величин

N

Jmn 1 =Z i=1

(n.y2 1 ( t i )• 2 2 ( t i ) 2 ²( (-)

n^ 2 ^ ) • 2 ‘ (^)

+ z -—-—------+ z     24 ti)

=2+,

(П.6)

Тогда

N N (n i X n j.) ² X⁽ t i ) • ² 2⁽ t j ) _ N ( п,У 2’ 1 ( t i ) • 2 2 ( t i )

J ^Z ; ^Z       2 ( t i ) • 2 ( t j )          ^Z         2 ²( t i )

N ni иmn 1

i = 1

² 2; < ц ) • 2 ;( ц ) 2 ²( t i )

+

N U \ 2 1 ( t i ) • 2 2 ( t i )    N N ^j ^{2 t i )} ' ^{2 2 (} t j )

= Z ,2i, . -------⁺ ZZ      2 ( t i ) • 2 ( t j )

i = 1             ^{2 (} t i )                 i = 1 j = 1

(П.10)

nn

+Z - i=1

^Х1(ti) • ^Vti)

+

22( ti)

Подставляя (П.10) в (П.2), получим обобщенное выражение для соответствующего элемента матрицы Фишера:

NN

+ ZZ

i = 1 j = 1

nniXnj ^^ti) ^ ^x2 (tj ) 2(ti) • 2tj)

(П.7)

N

J =У mn i=1

(п, \ 2 1 ( t i ) • 2 2 ( t i )

+

2 ²( (■)

¹ * ^j

NN

+ZZ

^{n п}^₅ ) ² 1 ⁽ t i ) • 2 2 ⁽ t j )

2 ( (■) • 2 ( t j )

(П.11)

С учетом того, что n i =n j при i=j , последний член (П.7) можно представить в виде следующей разности:

C N ( ⁿj) ² n ^{( t}j ) ^m j t !    2 ( t j )

N(n_f )2 L ( t, ) imj

Cn Z      A + Cm Cn j =1    2(t j )