Максимизация продольной электрической компоненты при дифракции на бинарном аксиконе линейно-поляризованного излучения

В соответствии со скалярной теорией дифракции, аксикон формирует бесселевый пучок нулевого порядка, диаметр центрального пятна которого по полуспаду интенсивности (FWHM) равен [1]:

FWHM = 0,36Х/ NA , (1)

где NA – числовая апертура аксикона.

Это на 30% меньше, чем диаметр диска Эйри, формируемого линзой с той же числовой апертурой (FWHM = 0,51λ/NA). Таким образом, вполне естественно использование аксикона при острой фокусировке [2, 3].

В работах [2, 3] было рассмотрено применение радиальной поляризации для формирования светового пятна, состоящего в основном из одной продольной компоненты, которое позволило достичь предсказанное скалярной теорией сверхразрешение по сравнению с линзой [1].

Однако большинство современных лазеров излучает линейно-поляризованный свет. Также достаточно легко можно получить круговую поляризацию. Генерация же цилиндрических пучков (с радиальной или азимутальной поляризацией) требует использования дополнительных довольно сложных и дорогостоящих устройств [4]. Таким образом, задача усиления продольной компоненты электрического поля в случае линейной поляризации является актуальной.

Управление вкладом различных компонент векторного электрического поля может быть полезно при оптическом манипулировании, использовании избирательно чувствительных материалов, для трёхмерно-ориентированного возбуждения флуоресцирующих молекул [5, 6].

Ранее было показано [7–9], что внесение вихревой либо линейной фазовой сингулярности в падающий пучок позволяет усиливать продольную компоненту на оптической оси в фокальной области. При этом был использован метод разложения по плоским волнам. Также было выполнено моделирование с помощью метода конечных разностей во временной области – FDTD. Сравнение результатов двух методов для би-

нарного аксикона приведено в работах [10, 11] и показывает их качественное совпадение при количественных различиях. Данные различия связаны с влиянием на результаты расчёта с помощью метода FDTD реальных оптических характеристик, таких как толщина подложки элемента, расстояние от источника до элемента [12]. Также влияние оказывает тип освещающего пучка, его размеры, длина волны излучения и материал, из которого изготовлен оптический элемент.

В данной работе решается задача максимизации продольной компоненты электрического поля при различных параметрах пучков, падающих на оптический элемент, а также параметров аксикона.

1. Исследование влияния типа пучка, падающего на бинарный аксикон

Рассмотрим бинарный дифракционный микроак-сикон:

T b(r) = ‘

exp

{ i arg |^ cos ( k a₀ r ) ] }

0, r > R ,

r < R,

с числовой апертурой NA= α 0 = 0,95, радиусом R = 4,462 X , который освещается излучением с линейной поляризацией. Внешний вид аксикона представлен на рис. 1.

Рис. 1. Структура бинарного дифракционного аксикона

Для моделирования дифракции различных пучков на аксиконе (2) использовался метод конечных разностей во временной области (FDTD), реализованный в программном пакете Meep [13]. Параметры моделирования: длина волны X = 0,532 мкм. Размер расчётной области x , y e [-6,5 X ;6,5 X ], z e [6 X ;6 X ]. Толщи-

на поглощающего слоя PML - 2 Х , шаг дискретизации по пространству - Х /30, шаг дискретизации по времени - Х /(60 c ), где c - скорость света. Толщина подложки аксикона равна 8 Х . Показатель преломления аксикона и подложки, в которой выполнен бинарный рельеф вида (2), n = 1,46. В этом случае высота микрорельефа составляет:

h =—^П— k ( n - 1)

« 1,087 Х .

В качестве падающего пучка была выбрана ограниченная плоская волна и гауссовый пучок с линейной y -поляризацией. Источник находится на расстоянии 2Х перед рельефом аксикона, внутри подложки.

Сравнение амплитуды двух пучков непосредственно перед плоскостью рельефа аксикона в различных сечениях (вдоль оси x и y ) показано на рис. 2. Видно, что ограниченная плоская волна при распространении теряет радиальную симметрию из-за линейной поляризации пучка.

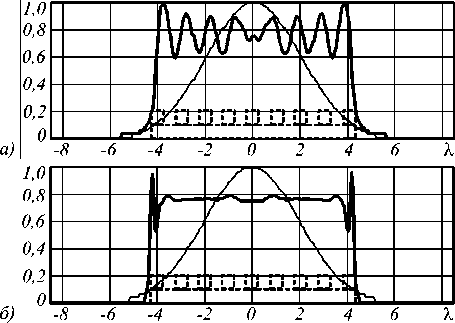
Рис. 2. Сравнение гауссова пучка и плоской волны: плоскость x (а), плоскость y (б), пунктиром схематично показан аксикон

Результаты моделирования дифракции при отсутствии и наличии в пучках фазового скачка (перпендикулярно плоскости поляризации) приведены в табл. 1–2. В случае гауссова пучка это соответствует использованию вместо фундаментальной лазерной моды пучка Гаусса–Эрмита (1, 0).

Как следует из табл. 1–2, линейная поляризация пучков сказывается и на асимметрии картины дифракции – происходит уширение фокального распределения вдоль оси поляризации. Это связано с наличием мощной продольной компоненты электрического поля, возникающей в фокальной области при использовании фокусирующих систем с высокой числовой апертурой. При этом интенсивность данной компоненты на оптической оси равна нулю, а основная энергия распределена в виде боковых лепестков вдоль оси поляризации.

Перераспределение энергии (концентрацию продольной компоненты на оптической оси) можно осуществить либо за счёт изменения поляризации пучка, либо за счёт изменения фазы [7–9].

Как видно из результатов, приведённых в табл. 1, использование моды Гаусса–Эрмита (1, 0) позволяет увеличить вклад продольной компоненты электромагнитного поля в фокусе, однако получить в общей интенсивности пятно меньше дифракционного предела не удаётся (из-за мощных боковых лепестков поперечной компоненты).

Преодоление дифракционного предела в общей интенсивности получено при освещении гауссовым пучком в направлении, перпендикулярном поляризации (FWHM( - ) = 0,44 Х ), при освещении же модой Гаусса–Эрмита (1, 0) такая возможность наблюдается только в продольной компоненте вдоль оси поляризации (FWHM z ( I ) = 0,43 Х ).

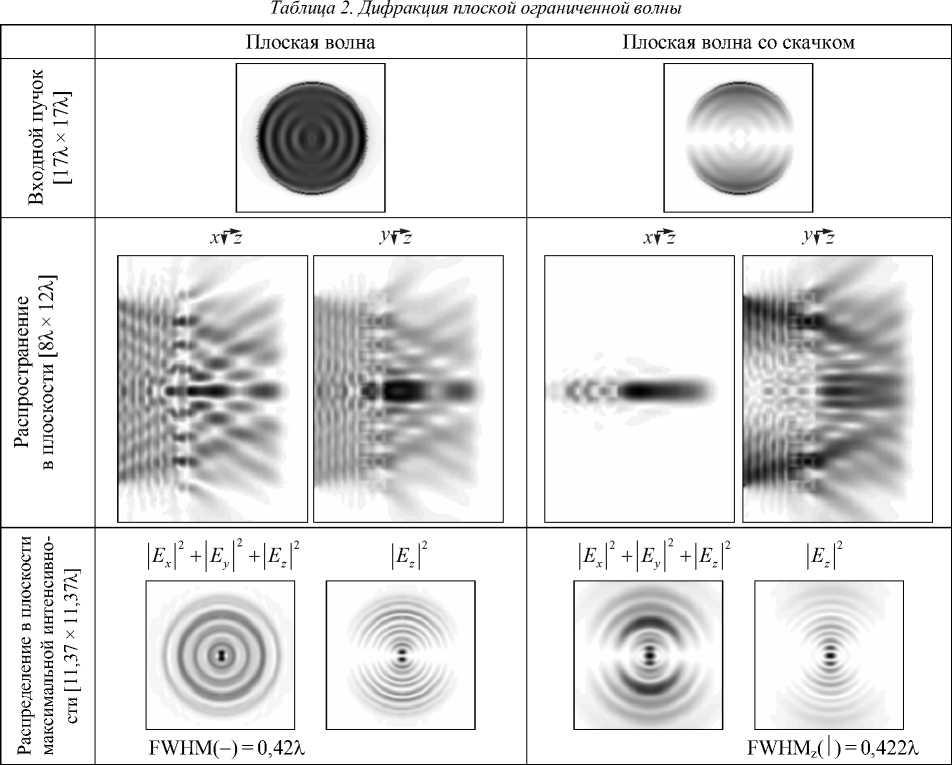
Для ограниченной плоской волны получились аналогичные результаты (см. табл. 2): FWHM( - ) = 0,42 X и FWHM z ( I ) = 0,422 Х соответственно.

Таким образом, не наблюдается какого-либо явно выраженного преимущества одного типа пучков над другими. Выделение продольной компоненты в данном случае не дало значительного уменьшения размера пятна, тем не менее, максимизация продольной компоненты таким простым способом может быть использована при оптическом манипулировании для ориентации молекул.

2.    Исследование влияния расстояния от источника до рельефа элемента

В отличие от ограниченной плоской волны гауссовы пучки при распространении в однородной среде меняют только масштаб. Поэтому, располагая источник непосредственно перед рельефом элемента и меняя размер пучка, можно таким образом варьировать расстояние от источника до оптического элемента.

Исследования проводились для моды Гаусса– Эрмита (1, 0). На рис. 3 показана дифракция в плоскости xz для различных размеров перетяжки ст .

Хорошо заметно, что увеличение радиуса пучка приводит к удлинению фокальной области вдоль оси распространения, однако в поперечном размере принципиального улучшения не происходит (поперечные изображения в плоскости максимальной интенсивности аналогичны приведённым в табл. 1).

Нужно отметить на рис. 3 появление слева от рельефа аксикона компактного светового пятна, сформированного внутри подложки за счёт отражённого от рельефа излучения.

3.    Исследование влияния материала оптического элемента

В настоящее время достигнутые пределы значений показателя преломления промышленных оптических стёкол составляют примерно 1,43 – 2,17. Нами было выбрано n = 2,0. В этом случае высота микрорельефа из формулы (3): h = 0,5 Х .

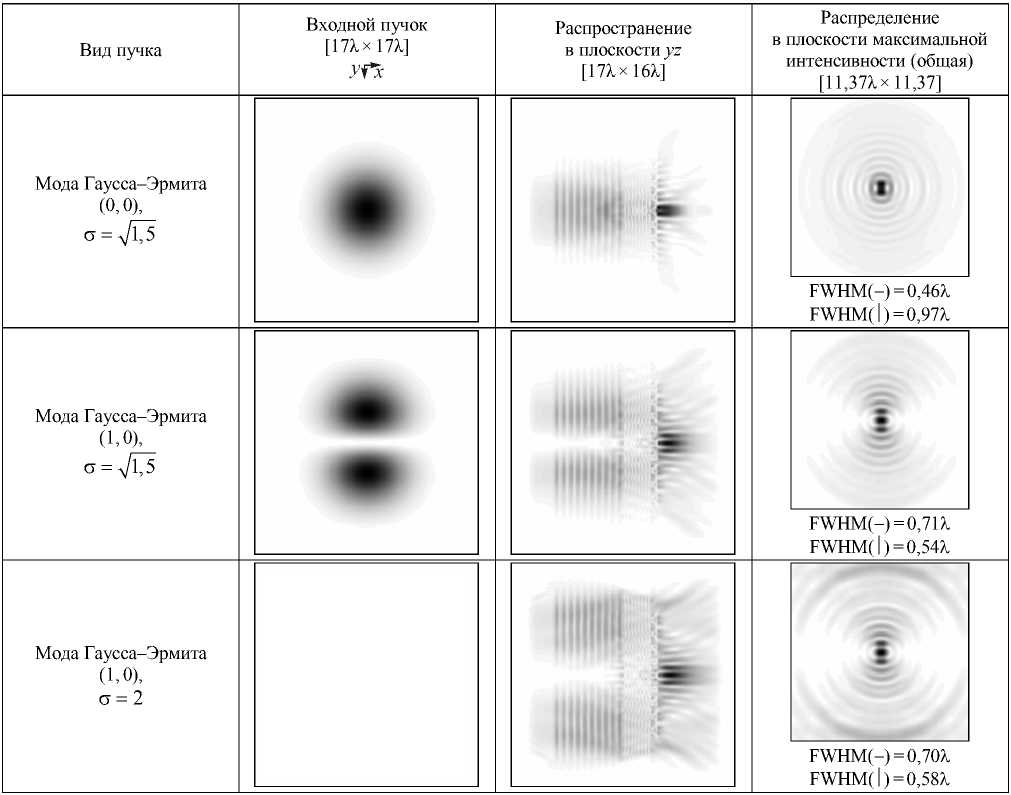
Исследования проводились для мод Гаусса–Эрмита (0,0) и (1,0) при размере перетяжки ст = д/1,5 и для моды Гаусса–Эрмита (1, 0) при σ=2. Результаты исследований приведены в табл. 3.

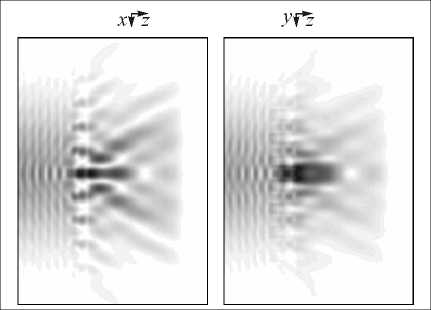
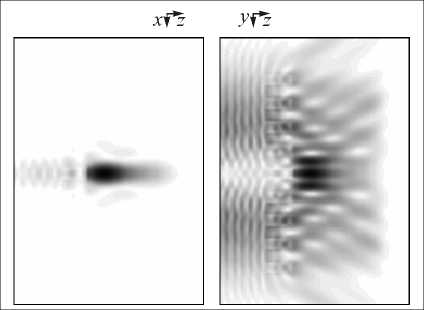
Таблица 1. Дифракция гауссовых пучков

	Мода Гаусса–Эрмита (0, 0)	Мода Гаусса–Эрмита (1, 0)
в о Kt У X О >> J X в р m	^^

в в в и В о н в в я о в в

§ в о к сЗ

-

У О О g

s в о

В

в

1,0

0,8

0.6

0,4

0,2

О

-8   -6   -4   -2

j^/W^

0.8

0,6

0,4

0,2

О

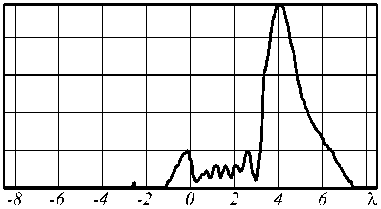
XT. E, | ¹ +| ^Ey |’ + | E, Г

FWHM(-) = 0,44X

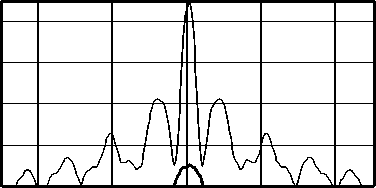
E z ²

I ^E , | ’ +1 E y Г +1 E J"

E z ²

FWHM z (l) = 0,43X

0.8

0.6

0,4

0.2

О

-4       -2        0        2       4   2

0,9

0.7

0,1

0,5

0.3

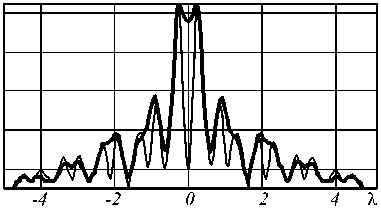
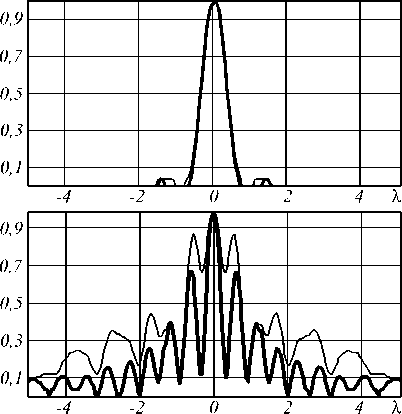
тонкая линия – общая интенсивность, толстая линия – компонента z

а)                              б)

Рис. 3. Распространение вдоль оси для источника рядом с рельефом аксикона [17 Лх 16Л ] : a = ^1,5 (а), а = 2 (б)

Отметим, что увеличение показателя преломления привело к увеличению продольной компоненты по отношению к поперечным и позволило сформировать отдельное компактное световое пятно.

Наилучший результат был получен для моды Гаусса-Эрмита (1,0) с перетяжкой g = д/1,5 (см. табл. 3). Следует также отметить, что после увеличения радиуса пучка фокальное пятно практически сохранило свою форму и размер, т.е. влияние уширения пучка несущественно.

Оценим также эффективность фокусировки по формуле:

s = I max ■ FWHM x ■ FWHM y IE о , (4) где I max – максимальная интенсивность в фокальном пятне, E ₀ – полная энергия в фокальной плоскости.

В табл. 4 приведены сводные значения поперечного размера фокального пятна по полуспаду интенсивности (FWHM) и эффективность фокусировки (4). Для рассматриваемой числовой апертуры (NA = 0,95) предел составляет 0,5368 X для линзы и 0,3789 Х для аксикона соответственно.

При оценивании влияния различных параметров также учитывалось расстояние от элемента до максимума интенсивности на оптической оси. В частности, для моды Гаусса–Эрмита (0, 0) данное расстояние составляет 0,012 Х при n =1,46 и 0,54 Х при n = 2, что говорит о значительном перераспределении в фокальной области. Также отметим уширение пучка по обоим направлениям, в особенности вдоль оси поляризации: от FWHM=0,86λ до FWHM=0,967λ. Таким образом, увеличение показателя преломления материала элемента привело к усилению продольной компоненты и одновременно к росту боковых лепестков.

Как видно из табл. 4, уменьшение толщины подложки приводит только к увеличению расстояния, на котором формируется пик интенсивности, на размеры и форму пятна оно не влияет.

Таблица 3. Дифракция гауссовых пучков при показателе преломления аксикона n=2

Заметим, что усиление продольной компоненты не всегда приводит к уменьшению размеров фокального пятна. Если же эта цель достигается, то эффективность фокусировки падает именно в связи с уменьшением площади центрального пика. Увеличить эффективность в этом случае можно за счёт увеличения показателя преломления и площади освещения фокусирующего элемента.

Заключение

В работе проведено моделирование дифракции линейно-поляризованного излучения на бинарном дифракционном аксиконе с высокой числовой апертурой методом FDTD.

Выполнено исследование влияния различных параметров пучков, падающих на оптический элемент, а также параметров аксикона с целью максимизации продольной компоненты электрического поля на оптической оси.

Для обычных пучков наличие продольной компоненты в фокальной области, возникающей при высоких числовых апертурах фокусирующих устройств, приводит к уширению фокального пятна вдоль оси поляризации – за счёт боковых лепестков, связанных с продольной компонентой.

Внесение фазового скачка в падающий пучок позволяет перераспределять энергию продольной компоненты, усиливая её интенсивность на оптической оси. Максимизация продольной компоненты таким простым способом может быть использована при оптическом манипулировании для ориентации молекул. Также при определённых условиях можно добиться формирования более компактного фокального пятна.

Преодоление дифракционного предела по сравнению с линзой было показано для различных типов пучков вдоль определённого направления.

Увеличение показателя преломления материала оптического элемента приводит к усилению продольной компоненты, а следовательно, к ухудшению ситуации для обычных пучков в связи с ростом боковых лепестков и улучшению ситуации для пучков с внесённым фазовым скачком.

Наилучший результат по формированию компактного фокального пятна, состоящего в основном из продольной компоненты, был получен для моды Гаусса–Эрмита (1, 0) с показателем преломления ак- сикона n =2. Размер пучка, падающего на аксикон, рах фокального распределения и может влиять не существенно сказывается на поперечных разме- только на протяжённость вдоль оптической оси.

Таблица 4. Параметры фокусировки рассматриваемых пучков

Вид пучка		Расстояние от элемента, λ	FWHM y , λ	FWHM x , λ	8
Мода Г–Э (0, 0)	Общая интенсивность	0,012	FWHM^, = 0,86 л	FWHM O,, = 0,44 Л	0,113
	Компонента Z		–	FWHM Z = 0,57 Л	–
Мода Г–Э (1,0)	Общая интенсивность	0,688	FWHM Z,, = 1,49 Л	FWHM Z,, = 0,76 Л	0,066
	Компонента Z		FWHM Z = 0,43 Л	FWHM Z = 0,73 Л	27,7%
Плоская волна	Общая интенсивность	0,030	FWHMay, = 0,9 Л	FWHM Z,, = 0,42 Л	0,348
	Компонента Z		–	FWHMx x = 0,57 Л	–
Плоская волна со скачком	Общая интенсивность	0,894	FWHMay, = 1,48 Л	FWHM Z,, = 0,72 Л	0,338
	Компонента Z		FWHM Z = 0,422 Л	FWHM' x = 0,7 Л	27,7%
Мода Г–Э (1, 0), n =2, G = л/1,5	Общая интенсивность	0,692	FWHMZ,, = 0,545 Л	FWHM Z,, = 0,708 Л	0,050
	Компонента Z		FWHM Z = 0,416 Л	FWHM^ x = 0,688 Л	74,2%
Мода Г–Э (1, 0), n =2, G = 2	Общая интенсивность	0,918	FWHMZ,, = 0,579 Л	FWHMZu = 0,699 Л	0,252
	Компонента Z		FWHM Z = 0,422 Л	FWHM^ x = 0,687 Л	71,6%
Мода Г–Э (0, 0), n =2, G = д/1,5	Общая интенсивность	0,542	FWHMZ,, = 0,967 Л	FWHM Z,, = 0,463 л	0,073
	Компонента Z		–	FWHMx x = 0,647 Л	–
Мода Г–Э (1, 0), n =1,46, источник рядом с подложкой, G = л/1,5	Общая интенсивность	0,753	FWHMZ,, = 1,488 Л	FWHM Z,, = 0,759 Л	0,111
	Компонента Z		FWHM Z = 0,430 Л	FWHMx x = 0,731 Л	10,0%
Мода Г–Э (1, 0), n =1,46, источник рядом с подложкой, G = 2	Общая интенсивность	0,903	FWHMay,, = 1,475 Л	FWHM Z,, = 0,742 Л	0,617
	Компонента Z		FWHM Z = 0,423 Л	FWHMx x = 0,716 Л	76,9%

Работа выполнена при поддержке грантов РФФИ 10-07-00109-а, 10-07-00438-а, гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9, а также ФЦП «Кадры» Минобрнауки (соглашение № 8231).