Малые колебания троса космического лифта

Рассматриваются малые колебания в плоскости экватора, гибкого нерастяжимого троса, закрепленного на экваторе, в гравитационно-центробежном поле. Такой трос является основным элементом космического лифта [1], и его динамика определяет характеристики всего сооружения. Исследование выполнено на. основе непрерывной математической модели, изложенной в [2, 3]. Рассматривается динамика, свободного троса, (без учета, движения кабины). Разработана, методика, вычисления собственных частот и форм линейных колебаний троса, найдены асимптотические по номеру моды формулы для этих частот и мод. Полученные результаты проверены и до некоторой степени развиты численными расчетами для нелинейной модели. Найденные разными методами результаты достаточно хорошо совпадают.

2.    Уравнения движения

Рассмотрим движение гибкого троса, в плоскости экватора, один конец которого закреплен на. планете, а. другой свободен, но на. нем закреплена, концевая масса. М. Введем систему координат, вращающуюся вместе с планетой с угловой скоростью ш, ис центром, совпадающим с центром планеты О. Ось Ох проходит через точку прикрепления троса, ось Oz направлена, вдоль оси вращения, а. ось Оу дополняет их до правой тройки векторов. Положение точки на тросе задается линейной координатой s, отсчитываемой вдоль троса от точки крепления троса к планете. Для компактности записи будем обозначать точками производные от переменных по t и штрихами - производные по s:

х 1

X = 2у ш + ш2х — и — +-- -— (Тх') , г³ p(s)

у =

^—2хш + ш^у ^— д^- +— — ^(Ту'У, г³    p(s)

х |_s=0= R;

•                      2     , ж Т ' ,

^{X — 2уш — ш ж} + р,^ + —X |₅₌д₊£= 0, г³  М

У |s=0= 0;

9 У Т , , у + 2хш — ш^у + д + —у l_s=_R+L= 0.

г³   М

В этом случае уравнения динамики такого троса записываются в виде (1) с краевыми условиями (2). Здесь L — длина троса, р = p (s') — линейная плотность троса в точке s, р — гравитационный параметр, Т = Т (s) — сила натяжения троса в точке s. t время, г — расстояние текущей точки троса, от центра. К уравнениям (1) и (2) необходимо добавить условие нерастяжимости троса. (3):

(ж')2 + (у')2 = 1.

Определение. Рабочим состоянием троса, назовем его вертикальную равновесную конфигурацию (4):

ж = R + s;   у = 0.

Будем считать, что трос состоит из двух компонент: несущей и дополнительной. Площадь поперечного сечения несущей компоненты обозначим S = S(s), ее объемная плотность ру, линейная плотность дополнительной компоненты постоянна по всей длине троса и равна ра. Тогда будем иметь р = Spy + ра. (5)

Для равнонапряженного троса Т (s) = S ( s)a, где константа у — допустимое по условиям прочности напряжение троса. В этом случае, известно из [2, 3], условие (6)

S = (So +   ) exp рУ ( U ( R e + s) - U ( R e )) -   ; U (г) = - Р - 2 ш²г ² .      (6)

U(r) — гравитационно-центробежный потенциал, So — площадь поперечного сечения троса, в нижнем сечении. Соотношения (4) - (6) полностью определяют равновесное вертикальное (рабочее) состояние троса.

Для изучения динамики троса, в окрестности этого состояния выполним линеаризацию задачи (1) - (3). Введем вариации ж1(s, t), y1(s, t), T1(s, t) переменных ж, у и Т, малые вместе со своими первыми и вторыми производными, так что ж = жо + Ж1, у = уо + У1, Т = To + Т1, где жo(s,t) = Re + s, yo(s,t) = 0, To(s, t) = S(s)y.

В дальнейшем будем пренебрегать членами выше первого порядка относительно жц уі, Ті. Из условия нерастяжимости (3) следует Ж1(s, t) = 0, г = жо = R e + s, а изменение сечения вдоль троса дается формулой (6). В результате линеаризации и замены у 1 = ( R e + s)y1 получаем краевую задачу (7) на вариации у 1 и T₁(s,t):

Т ' 0 = 2 w ( R e + s)yi + -¹, р

^У1 = р(, + r e )2 ^W‘ ^{+ RE)2У;)}''

2 R e + Г)№) - Д 0   у 1 + ^У1 = 0.

3.    Разделение переменных

Из (7) выделяется краевая задача на вариацию yi(s,t). В дальнейшем индекс «1» при обозначении вариаций будем опускать.

Воспользуемся методом разделения переменных и будем искать решения в виде ряда y(s,t) = ^Y k ( s )Ө k (t), г де Y k ( s )Ө k (t) — частные решения системы.

k

П         ¹               Ч² v'\'n    ^Өk        ^{+ R}E'V^kV

• ^YkӨ = p ( s + R e )^{2 (То}^ ^{+ Re} ) ^Yk) ^Өк ^ Өк = p ( s + R e )²Yk = ^Xk = const.

Далее покажем, что А& > 0, поэтому Ө _к = А _к cos(ДД t + P k ) ^— решение вспомогательной задачи.

(To(s + R e ) 2 Y fe ) ’ + A _k p ( s + R _e )² Y = 0;

Y k (0) = 0;   T o ( L ) Y^ ( L ) - A _k MY _k ( L ) = 0.

Для Y _k находим краевую задачу (8), где A _k — спектральный параметр. Это задача Штурма-Лиувилля, в решении которой и состоит основная сложность. Здесь А _к входит в краевое условие, что не позволяет использовать в данном случае стандартные результаты теории Штурма-Лиувилля.

В дальнейших выкладках индексы к опущены.

Утверждение 1. Собственные значения вещественны и положительны, а собственные функции ортогональны.

Доказательство. Интерпретируем задачу (8) как поиск спектра дифференциального оператора D;

(To(s + R e ) 2 Y ‘)‘ p ( s + R e )²

.

Данный оператор действует на множестве В функций из С ²[0, L], удовлетворяющих краевым условиям из системы (8). В — линейное пространство в силу того, что оба ограничения линейны. Введем на множестве В скалярное произведение:

L               L

( u,v) = J u ( s ) v ( s ) dp = J

u ( s ) v ( s ) p ( s + R _e ) 2 ds + Mu ( L ) v ( L )( L + R _E )².

Оператор D является симметричным оператором относительно введенного скалярного произведения. Действительно, с учетом формул (8) имеем

MDu ( L ) v ( L )( L + R e )² = -T o ( L + R e ) 2 u‘ ( L ) v ( L ) .

Поэтому

L                                                   L

( Du, v ) = j( T o ( s + R e ) 2 u‘ ) ‘vds - T o ( L + R e ) 2 u‘ ( L ) v ( L ) = - j T o ( s + R e ) 2 u‘v‘ds = ( u, Dv ) .

Отсюда следует вещественность собственных значений оператора и их ортогональность. Из полученного равенства легко видеть, что оператор D является отрицательно определенным, а равенство ( Du,u ) = 0 достигается только при u = 0. Утверждение доказано.

4.    Асимптотика собственных значений и собственных функций

Для упрощения дальнейших действий введем следующие обозначения:

А = х 2 ;	T 0 (s + R e )2 P1(s) =       2	(To ( s + R e )2) ;   P 2 (s)   To
	^(s) = V№(s);	^^(s) = J ^( T ) dT.

Заменой Y = ((s + R e )VT0) 1 Y система (8) сводится к краевой задаче (9):

Y ‘‘ + P 1 Y + xW = 0;

′2

^Y(0) = ^{0; Y}‘^(L) ' ^L A; L ⁺ l + r E ⁺ TL)⁼⁰'

Для этой задачи выполняются следующие условия:

• 1)    функции Р 1 Е С 1. Р 2 Е С 2.

• 2)    P2(s) >  0, поэтому корни Фі, Ф2 характеристического уравнения Ф² + P2(s) = 0 различны между собой: Ф₁(s) = iQ(s), Ф₂(s) = —^(sY

В работе [5] показано (см. также [6], [7] и [8]), что фундаментальная система, решений для задачи (9) представима, в виде (10) при выполнении условий 1) -2).

∞

Е « k,j ^(s)X ^{-: >} I , ^k = 0,1.

3 =0

Здесь -k,j(s) - некоторые непрерывно дифференцируемые функции. Подставляя эти решения в дифференциальное уравнение в системе (9) и заменяя Vk,j = tik,jП 2, находим

^-k,0 = ⁰;   ^-'k,j = ^{(— 1)k}г Q^{n 2} ( ^-kj-iQ ² ) ⁺ у^{П 1 -}k,j - i^ .

Для упрощения дальнейших выкладок введем новое обозначение а/=£ х2 ^п-2У'+P1 ""^

Из полученных уравнений следует рекуррентное соотношение для функций 1^ 3:

• ^- к, 0 ^C k, 0 ; ^— к,з     ^C k,j ^{+ (} 1) ^гА— k,j — 1^.

Здесь C k,j - это константы интегрирования.

Отсюда находим следующее выражение для функций —.ф

• ^- k,3 = '^2^{(( — 1)k}i Y ^AlC k,j - l .

l =0

Подставляя выражение, полученное для нқр ^в (10), находим функции, определяющие фундаментальное решение краевой задачи (9):

( го 3

ЕЕ ■'А cm- i : х^-3 1 .

3=0 l=0

Переставляя порядок суммирования в получившемся ряде, находим пару независимых решений дифференциального уравнения (9).

exp ( (—1)^kгх Пы) ^го

«k (s,x) = —------1 Е((—1)^{k і}) ¹ a¹: X- .                 (11)

V П       l=0

Решения краевой задачи (9) будем искать в виде линейной комбинации функций

«о^(s,X) = -М^хН M^X ) , V i ^(s,x ) = V0^(s,x^{) —} « 1 ^(s,x ) .

Отметим следующие свойства оператора А:

(А/) |s=o= 0;

( ' + А2 ) ^-1А = А ( z + А 2 )

Используя П(0) = 0, находим, что «1(0,х) = 0, а «0(0, х) = 2П 1/2(0) = 0.

Следовательно, собственные функции краевой задачи (9) имеют вид

"(s, х) = П ^1/2 ^sin ( хП ) ( ^ +    )

(1) + cos ( х^П ) Q +    )   ^А1) .

Возвращаясь к представлению обратного оператора в виде ряда и подставляя полученный результат в краевое условие при s = L, находим

sin ( хіі ) (»5 П - MX2) + cos ( хіі ) "К = ІС(-1)V ПМ21 + Т - ПА22+1 j =0       \ - cos = :b (-dV §)А21+1+ d-Adsi - пА21+2 1=0       \

("^+(П - ММА)х)_ =0; ( T0(s + Д е )2 ) 21 M ^21+2 ^ 2j, 2To(s + Д е ) 2 А + T „ A х     ' (Ж ^ ДДе) 2 ! ^21 + 1    М д21+з \ .-21-1 2To(s + Д е ) 2 А    +T 0 A х

Собственные значения ищем в константы. Тогда

∞ виде ряда х(п) = хо(п) + D хгп-\ гДе хг - некоторые i=1

F (s)

хо(п) = тnП(L) ;

Vp ( L ) T o ( L ) - MF ( L ) тМ

1 І ⁽ To⁾⁴ ( ⁽ To⁾⁴ ^ ‘‘ ₊ To(s + R e )²

2 У Ip p                2

( To(s + Д е )²

ПT)2

ds.

Подставляя полученную асимптотику в формулу для собственной функции, находим

"п(в,х)=П 1/2

Q(s)

Sin тп +

П( Ғ )

+ — cos тп

pTO

M

s = L

Q(s) - F (L)Q(s) + n( L ) F (s)

Возвращаясь к X _n и Y _n (s), получаем следующие выражения для собственных значений и функций:

L

Ап = т2п2

'o(L)

-

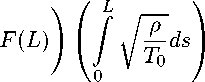
-1

Y„(s) -(« s + Д е ~

Q(s)

Sin тп + ^L)

+ ПУсо= тп

(тп      (

П( Ғ )

(p(L)To(L))1/2 Q(s)

M     n(L)

-

^{F (L)}s|^+F(s)))'

Выписанные формулы дают асимптотические приближенные для собственных значений и функций при больших п, а для точных вычислений при малых п использовался алгоритм, описанный ниже.

5.    Алгоритм вычисления собственных значений и собственных функций

Следуя методике, изложенной в [9], сделаем замену

T o ( s + R e )²Y‘ = d(s) cos y(s);

AM ( L + R e ) ² Y (s) = ri(s) sin y(s).

Поскольку T(s) > 0 и У(s) и Y‘(s) одновременно не равны нулю, то эта замена взаимно однозначна и d(s) = 0. Подставляя в (8) соотношения (14), получаем ri’

/         P^(R e + ^s)2 ,

= ^ytgy - M ( R e + L)2^{tg y;}

sin у (0) = 0;    d ( L ) cos у (L) — d ( L ) sin у (L) = 0.

Без потери общности можно считать, что у (0) = 0. Из второго краевого условия получаем, что tgy(L) = 1. Дифференцированием второго равенства (14) вместе с полученным выше соотношением получаем независимую краевую задачу (15) для у:

‘ _ AM ( R e + L)²   2 ₍ p( R e + s)² .2

^У     T ( R e + s)² cos ^{У +} M ( R e + L)² sin ^У;                 (15)

y(0) = 0; tgy(L) = 1.

Докажем теперь, что существует бесконечное число значений А^ (к = 0, 1, 2, ...), для которых краевая задача. (15) имеет решение.

Лемма 1. Пусть у ( х, а) - решение з;щачи Коши у ' _х = д ( х, у, а ) ,у (0) = 0. при чем д ( х, у, а) строго возрастает по а при х G [0,L),y > 0. Тогда Vxо G [0, L) у(хо,а) возрастает по а. Если хо < L, то возрастание строгое.

Доказательство. Допустим а < b и  у(хо,а)    >     у ( х о ,Ь).  Пусть

I := max{x G [0;хо] : у ( х,а ) <у ( х,Ь ) }. Тогда

д⁽^ у0, ^{а),а) —} д⁽^ у0, ^b),b) = у‘0, ^{а) —} у'О,^b) =

у⁽/ ⁺ ф ^{а) —} у⁽1, а ) ^— у⁽/ ⁺ h, ^{b) +} уД ^b) lim ------------------------------------ > 0

Һ^+о                  h так как сумма, нечетных слагаемых в числителе по предположению положительна, а. четных равна нулю. Но это противоречит строгому возрастанию функции д по последнему аргументу.

Следствие. Если у аД) - решение задачи (15) без второго краевого условия, то У аД) возрастает по А. (Вытекает из доказанной леммы, т.к. правая часть уравнения для у из (15) монотонно возрастает по А.)

После вычисления собственного значения соответствующая ему собственная функция находится совместным интегрированием уравнений в переменных ri и у:

‘ _ ^{Ам (R}e ^{+ L)2}   2      ^p(R E ^{+ s)2} . 2

^У = T ( R e + s)² cos ^{У +} M ( R e + L)² sin ^У;

‘ _  АМ ( R e + L)²

^{Й   ri(} T ( R e + s)²

-

P^(R e ^{+ s)2}

M ( R e + L ) 2 ^{)siny cosy}'

и затем от этих переменных нужно вернуться к исходным по формулам (14).

6.    Численное изучение малых колебаний космического лифта

Результаты описанной выше работы использовались для расчетов в программах, численно моделирующих движение лифта в нелинейной модели. Во-первых, это служит обоюдной проверкой численных и аналитически полученных результатов. Во-вторых, численные результаты дополняют аналитические, например, исследованием влияния движения троса на напряжение в нем. Численные результаты также позволяют определить границы применимости линейной модели.

При вычислениях собственные формы линеаризованной задачи задавались как начальные формы троса. Результаты расчетов показаны на рис. 1 на примере первых 8 мод колебаний. Для наглядности на каждой фигуре рисунка изображены положения троса через некоторые интервалы времени для одного движения. Рисунок растянут по горизонтальной оси, т.к. отклонение составляет порядка 0.001 от длины. (На дальнейших рисунках изображения троса тоже растянуты по горизонтали.) При достаточно малой амплитуде колебания получаются периодическими. Узлы остаются на месте на протяжении десятков периодов. Это показывает соответствие численных и аналитических расчетов.

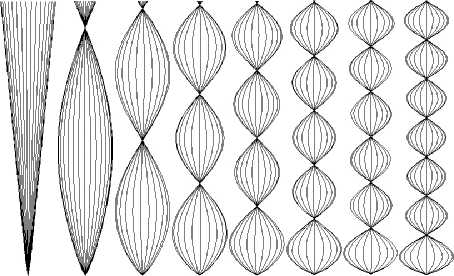
Рис. 1. Первые собственные моды колебаний

Здесь можно видеть собственные формы колебаний, п-я собственная форма имеет п пучностей и п + 1 узел и близка к синусоиде, у которой на длине троса располагаются п/2 периодов (хотя синусоидой, конечно, не является). В случае четной собственной моды п при разложении в ряды Фурье отклонений от вертикали преобладает одна (п/2) мода Фурье, в случае нечетной собственной моды п — две ((п — 1)/2, (п + 1)/2).

Поведение напряжения в линейных колебаниях. Вариация 6Т (s,t), то есть поправка 1-го порядка к силе натяжения троса, раньше не вычислялась, так как с точностью до линейных членов не входит в уравнения для вариаций отклонений. Из формул для уд—ф из (1), (2) следуют соотношения

—--+ 2шеp5v = 0, 5Т(L, t) — 2шеM5v(L, t) = 0, os

которые представляют собой дифференциальное уравнение для 6Т ( s,t и краевое условие. Отсюда 6Т (s,t) находится квадратурой

5Т ( s,t = 5Т ( L,t) + 2 w E

L j p(g)Sv(£,t)d£,

S

= 2 ш е

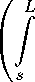
p(£)M£,t)d£ + M5)

Подставляем вариацию скорости 6v ( s, t ) как производиую по времени бу;

^бТ = ²ше ^ А _к Ө _к (<)Ек^(s), к

где Ak — амплитуда колебаний k-й моды, Sk(s) = модовых колебаний

( ^J Y k Сент +Yk ( l )m^

. Для одно-

^5Т = 2 ш е ^А к Ө к ^(t)sk^(s).

Если при t = 0 трос неподвижен и форма его соответствует к-й моде колебаний, то

5y ( s,t = А к Yk (s)cos( V^ k t ) ,5v ( s,t ) = -А к Yk (s) V^ k sin( V^ k t ) .          (19)

Формула (17) принимает вид

5Т (s,t) = -2 ш _е A k V^ k sin( V^ k t )s k (s).                       (20)

Напомним, что Т ( s,t ) = То (s) + 5Т ( s,t ) г де То — сила натяжения в вертикальном неподвижном тросе. Из (17) видно, что сила, натяжения изменяется периодически по времени и достигает экстремумов со сдвигом по фазе на. четверть периода, по сравнению с поперечным отклонением 5у. Т совпадает с То, когда фаза Д^к t = лп. то есть когда отклонения троса принимают амплитудные значения п Е Z или когда Sk(s) = 0. Заметим, что вариация силы натяжения в точке синфазна или противофазна скорости 5v ( s,t ) в (16), в зависимости от знака выражения Sk(s). Вообще, знак этого выражения может меняться вдоль троса. Видно еще, что вариация натяжения пропорциональна амплитуде Ak, которая определяется из начального отклонения.

Для вычисления напряжения a ( s,t ) разделим натяжение в точке на площадь сечения:

a ( s, t) = ао + 5а = ао + 2 ш _Е O k (t) Ak

^Sk^(s) S ( s )

Или, в другой форме:

L

M5v k ( L,t ) + J p« ) 5i> k ( C,t ) d<

a ( s, t) = ао + 5a = ао + 2 ш _Е

s

-

где ао - номинальное напряжение, то есть напряжение в вертикальном неподвижном тросе. Для равнонапряженного троса ао >  0 — константа.

Трос может порваться, если напряжение больше разрывного напряжения а^г, которое является характеристикой материала. Но при малых колебаниях напряжение не приближается к разрывному, поскольку номинальное напряжение ао выбирается с запасом прочности. Напряжение в рассматриваемых примерах меняется мало — на 0.1-0.01% от начальной величины, но ведет себя достаточно интересно.

Например, на. рис. 2 представлены парами профиль троса, и напряжение в один и тот же момент времени.

Начинается движение с гладкой кривой напряжения, в которой напряжение монотонно убывает (2а), потом быстро образует волнообразную кривую, у которой столько экстремумов, сколько узлов у собственной формы троса. (26). Такая примерно форма, кривой напряжения держится до половины периода. Амплитуда, колебаний напряжения увеличивается по мере движения от крайнего положения до среднего, т.е. при фазе от 2 п⁽ до (2 п + 1)( (2в — четверть периода), и уменьшается при движении от среднего положения к крайнему, т.е. при фазе от (2 п + 1)( до (2 п + 2)(, п Е Z. Потом на половине периода кривая становится монотонной (2г), затем перегибается в обратную сторону, т.е. образует столько же экстремумов (по числу узлов исходной формы), но минимумы и максимумы поменялись местами. И держится в таком виде еще полпериода.

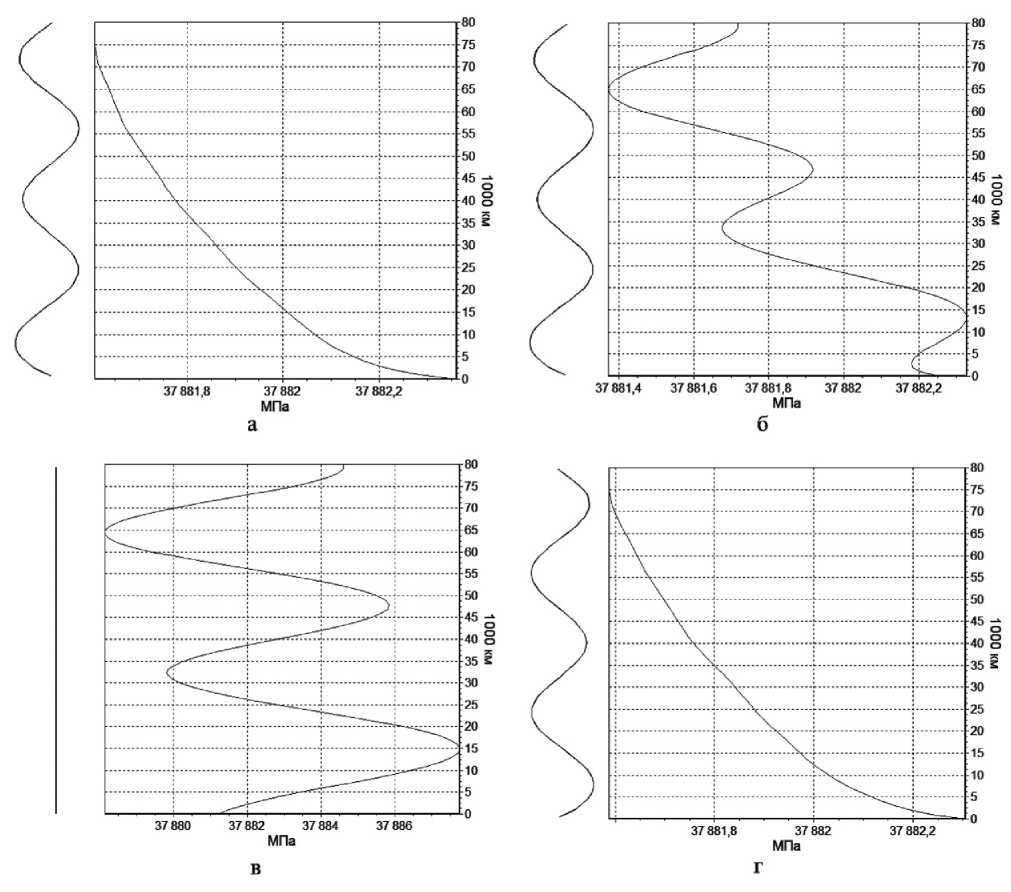
Рис. 2. Пары - профиль троса, и напряжение в один момент времени

На следующих рисунках для наглядности изображены положения троса, через некоторые интервалы времени, как на. рис. 1. Чтобы отразить на. том же рисунке изменение напряжения, участки с разным напряжением показаны разным оттенком. Кривые, соответствующие разным моментам времени, могут накладываться, более поздние перекрывать более ранние. Наблюдаются несколько интересных эффектов.

На рис. 3 показаны колебания для 14-й моды. Участки троса, с напряжением больше номинального сто закрашивались более светлым цветом, меньше - более темным. Напряжение больше при более прямом тросе и меньше при амплитудных значениях. Этот эффект наблюдается на. более высоких модах, где напряжение сильнее зависит от фазы движения, от того, находится ли трос в самом изогнутом положении (время кратно половине периода) или распрямлен (время составляет нечетное число четвертей периода). Скорее всего, большее напряжение при прямом тросе объясняется большей скоростью (22), которая в свою очередь математически объясняется большим множителем V^fe (19), а физически - тем, что колебания высоких мод более высокочастотные.

Иногда, на. протяжении всего движения напряжение на. одном участке троса, почти не меняется. На рис. 4а. изображена, первая половина, периода, на. рис. 46 — вторая, дальше все продолжается периодически. Рисунок выглядит сплошным, потому что положения троса, отрисовывались часто. Окраска следующая: номинальное напряжение обозначено серым,

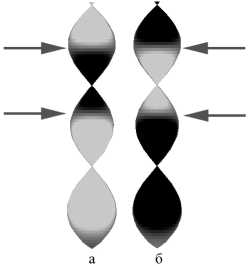
Рис. 4. 1-я и 2-я половины периода. Стрелками показаны участки с почти постоянным по времени напряжением

Рис. 3. 14-я мода чем напряжение больше, тем цвет светлее, чем меньше, тем темнее. Показаны стрелками два узких участка троса (две серые полосы), на которых напряжение практически сохраняется. Остальные участки троса кажутся черными или светло-серыми потому, что вариация напряжения на них, хотя в абсолютном значении мала, значительно больше вариации напряжения на участках постоянства напряжения, которая почти равна нулю. Видно, что 1-я и 2-я половины периода «инвертированы» по напряжению. Этот эффект наблюдается на низких модах.

Существование же участков, на которых напряжение почти не меняется, связано с тем, что для этой формы троса находятся координаты s, при которых L

E_k (s) = fYk(0р(^)d$, + У_к (L')M = 0, то есть 8a обращается в 0 (см. формулу (21)). S

Границы линейности. Вычисления показывают, что периодичность сохраняется при отклонении порядка десятков километров (для более низких мод больше, для более высоких - меньше), т.е. для отклонения порядка 0.001 от длины. Данная работа продолжает и развивает результаты, изложенные в [2], [3]. Она позволяет связать аналитические результаты для линейных колебаний с численными результатами, изложенными в [2]. Возможно дальнейшее развитие, и полученные данные (в частности, собственные формы) могут дать новые инструменты для изучения нелинейных колебаний.