Малые подграфы и расширения в семействе случайных подграфов плотных дистанционных графов

1.    Введение и история задачи

Исторически первая (и наиболее изученная) модель случайного графа G(n,p) была предложена. П. Эрдёшом и А. Реньи в 1959-1960 гг. (см. [1,2]). В ней все (неориентированные) ребра проводятся независимо друг от друга с вероятностью р. Если точнее, случайный граф G(n,p) есть случайный элемент, принимающий значения в множестве всех неориентированных графов на п вершинах с раопределением P(G(n,p) = (К, Е )) = р^|Е|(1 — р)^С" ^-|Е| (здесь К — это множество вершин графа — некоторое фиксированное множество мощности п, а Е — множество ребер — множество пар элементов К). Достаточно полное описание результатов, посвященных G(n,p), можно найти в [3-7].

Естественное обобщение этой модели получается, если ребра проводятся не все возможные, а принадлежащие множеству ребер некоторого графа G. Соответствующий случайный элемент в такой постановке называется случайном подграфом G_p графа G.

Одной из важных проблем в теории случайных графов Эрдёша-Реньи является нахождение предельного распределения малых подграфов в G(n,p). Первые результаты были получены еще самими П. Эрдёшем и А. Реньи [2], а. позже этим вопросом занимались Б. Боллобаш [8], А. Ручински, Э. Винс [9] и др. Приведем формулировки основных теорем, но прежде дадим основные определения.

Пусть Л = Л(п) — произвольное свойство графов. Формально под свойством графов для некоторого п понимается любое подмножество множества всех неориентированных графов на п вершинах. Примерами таких свойств являются свойство содержать некоторый

фиксированный граф в качестве подграфа, свойство графа быть связным, свойство графа иметь хроматическое число, равное пяти. Пороговой вероятностью свойства Л для случайного графа G_p называется такая функция р* = р*(п), что lim_n^^ Р(Л) = 0 пр и р = о(р*), п — то, и lim_n^^ Р(Л) = 1 при р = w(p*), п — то (или наоборот). Здесь /(п) = о(д(п)~) (/(п) = w(g(n))) означает, что для любого С > 0 сущеетвует пд > 0, такое, что для любого п > пд выполнено |/(п)| <  С |д(п) | (С|д(п)| < |/(п)|). Для этих отношений мы также будем использовать обозначения / (п) ^ д(п) и / (п) ^ д(п) соответствен но. Функция р* = р*(п) называется точной пороговой вероятностью, если для любого с < 1 при р 6 ср* выполнено lim_n^^ Р(Л) = 0 и для любого с >  1 пр и р > ср* выпо лнено lim_n^^ Р(Л) = 1 (или наоборот).

Будем обозначать и(Ғ ) и е(Ғ ) количество вершин и количество ребер графа Ғ соответственно. Напомним, что граф Ғ называется строго сбалансированным, если

р(Н ) <  р(Ғ )

для любого собственного непустого подграфа Н С Ғ, где р(Н ) = е(Н)/г(Н) — плотность графа Н. Граф называется сбалансированным, если неравенство нестрогое.

Максимальной плотностью графа Ғ называется величина

„ max              е(Н )

р   (^Ғ )= max .

нсғ и(Н ) цн )=д

Теорема 1 (Б. Боллобаш [8]; А. Гучински, Э. Вине [9]). Пусть Ғ — произвольный фиксированный граф. Тогда функция р* = п^-1/^^тах(ғ) является пороговой вероятностью свойства содержать копию Ғ для случайного графа G(п,pY Выполнен также закон больших чисел для числа копий Хғ графа Ғ в G(п,p): при р » р* для любого е >  0

P

Хғ

ЕХғ

— 1

< е^ —— 1.

Теорема 2 (Б. Боллобаш [8]). Пусть Ғ — строго сбалансированный граф с к вершинами и l ребрами а а — количество его автоморфизмов. Пусть р ~ сп ^к/. с >  0. Тогда распределение величины Хғ слабо сходится к пуассоновскому с параметром X = с¹ /а.

В настоящей работе мы получили ряд результатов об асимптотическом распределении малых подграфов в семействе других моделей случайного графа, называемых случайными дистанционными графами, определение которых будет дано в следующем разделе. Эти результаты распространяют утверждения, доказанные в [10], на более широкий класс графов.

Перейдем к описанию свойств расширений, являющихся обобщениями свойства содержать некоторый фиксированный граф.

Пусть Н — граф с вершинами zi,..., zn, Уі,..., Pk- где R = {zi,..., zn} — множество корней. Сетью называется пара (R,Н ). Говорят, что граф G удовлетворяет свойству расширения Ext(R, Н), если для любых u₁,...,un Е V (G) найдутся такие Wi,...,Wk Е V (G) \ {v1,... ,Vd}- что {zi,yj } Е Е (Н ) ^ {ui,Wj } Е Е (G) для любых г Е {1,..., d}. j Е {1,... , к} ii {y_t, Pj } Е Е(Н ) ^ {w_t, Wj } Е E(G) для лтобых г, j Е {1,..., к}.

Пусть l = е(Н ) — е (Н |д), где Н |д — подграф Н, индуцированный на множестве R. В общем случае величины к ii l будем обозначать v(R,Н ) 11 e(R, Н) соответствешю. Величина р(R,Н ) = l/к называется плотностъю сети (R,Н ). Подсетью называется сеть (R, S') := (R,Н І5), где R С S С V(Н ). В собственной подсети S = V(Н ). Сеть (R,Н ) называется строго сбалансированной, если p(R, S ) <  p(R, Н ) для всех собственных подсетей (R, S ). Она называется сбалапсированной, если неравенства, нестрогие. Сеть (R, Н ) называют нетривиальной, если каждая корневая вершина z соединена ребром в Н с хотя бы одной вершиной у Е V(Н ) \ R.

Дж. Спенсером в [11] была, доказана, следующая теорема.

Теорема 3 (Дж. Спенсер [11]). Пусть (R, Н) — нетривиальная строго сбалансированная сеть. Тогда существуют такие числа 0 < е < К, что если р 6 en-fc//(lnп)1/1, то lim P(Ext(R, Н)) = 0; n^^

если р > Кп~^к/ (ln п)¹/¹, то lim P(Ext(R,H)) = 1.

n^^

Верно и более сильное утверждение. Пусть ci есть число автоморфизмов графа Н, оставляющих корни на своих местах. Пусть, кроме того, с2 обозначает количество биективных отображений R на себя, которые можно продолжить до некоторого автоморфизма Н. Если А = const > 0 и для р = р(п) выполнено пкр1 /ci = ln (п^/(с2А)) , то lim P(Ext(R, Н)) = е-Х. n >^

2.    Описание модели и новые результаты

В этом разделе мы определим случайные дистанционные графы и приведем формулировки доказанных нами теорем для этой модели, аналогичных теоремам 1-3 из предыдущего раздела.

2.1.    Основные понятия и формулировки теорем

В настоящей работе рассматривается семейство полных дистанционных графов

G = G(п,ап,а²п) = (V, Е ), а = ¹, а1 ,а₂ Е N, Н ОД(а1,а₂) = 1, п = 0 mod а2, «2

в которых

V = {x Е ^{0,1}n : ⁽х,х) = ^аЦ, ^Е = {{x,y^} : ⁽х,y) = ^—2^п} , где (x, y) обозначает евклидово скалярное произведение.

Эти графы называются дистанционными, посколвку их ребра соответствуют парам вершин, находящихся на определенном расстоянии друг от друга. Подобные графві играют важную ролв в различных задачах комбинаторной геометрии (см., например, [12-16]).

Количество вершин этого графа будем обозначать N = N (п), а его степень (граф, очевидно, является регулярным) — Ni = Ni(n). Заметим, что в силу формулы Стирлинга

„ Н (a)n an °n   Д2^адн, е^

• ¹   <„. Sⁿ ~ 2^—312Р3І2П¹

где 3 = 1 — а, а Н (а) = —а ln — — 3 ln 3 функция энтропии.

Нас интересуют случайные подграфы G(п, ап, а²п), которые мы будем далее называть случайными дистанционными графами G_p(п,ап,а²п). Не опасаясь путаницы, в дальнейшем мы часто будем записывать G и G_p вместо G(n, ап, а²п) и G_p(п, ап, а²п) соответственно.

В статье [10] были получены результаты для G(n, п/2, п/4), аналогичные приведенным результатам для случайного графа G(п,р). В настоящей работе мы обобщаем эти теоремы на случай произвольного а. Будем использовать обозначение Хр для числа копий графа F в случайном графе G_p. Сформулируем полученные результаты.

Теорема 4. Пусть Ғ — произвольный фиксированный граф. Тогда функция

_р* = _N-1/pmax (F ) Л ^р             N1

является пороговой вероятностью свойства G_p(п, ап, а²п) содерэюатъ копию Ғ. При р ^ р* для любого е > 0

^P ( E X f -¹<^е) ^ ^1.

Теорема 5. Пусть Ғ — строго сбалансированный граф с к вершинами и I ребрами и а есть число автоморфизмов Ғ. Пусть р ■ cN-k/l N,

N1

где c = const > 0. Тогда распределение X f слабо сходится к пуассоновскому с параметром А = c^l /а, где X f — число к опий графа Ғ в G_p(п, ап, а²п).

Перейдем к свойствам расширений. Такие свойства являются монотонными (см., например, [4]) и поэтому для них существуют пороговые вероятности (см. [4]). Тем не менее, как показано в [10], для многих сетей (R, Н) и для любых р свойства Ext(R, Н) с вероятностями, стремящимися к 1, не выполнены для некоторых подпоследовательностей случайных дистанционных графов G_p(n, п/2, п/4). Аналогичные наблюдения могут быть сделаны и для графов G(n, ап, а²п). Поэтому для подобных свойств расширений пороговую вероятность не удается представить в удобном виде, как это сделано в теореме 3 для случайного графа G(п,p). В этой связи, действуя аналогично случаю а = 1/2 из [10], мы модифицировали определение свойств расширений для «дистанционного случая», сузив семейство множеств корней. Определим эти свойства.

Пусть f = f(п) — произвольная последовательность положительных чисел. Также пусть (R, Н) — нетривиальная строго сбалансированная сеть с V ( Н) = {щ,..., Zd,P1,... ,Ук}, R = {щ,..., Zd} и e(R, Н) = I. Рассмотрим произвольные вершины v1 =  (-01,...,Е),...,vd  =  (v^...,-^)  Е  V. Обозначим 51,...,52d  Е  {0,1}d раз личные d-последовательности из нулей и единиц, упорядоченные лексикографически: 51 = (1,..., 1) > ... > (0,..., 0) = 62d. Разобьем множество {1,...,п} на подмножества B1,...,B2d следующиеi образом: г Е Bj тогда и то.тько тогда, когда (u1,...,ud) = 5j. Положим

Xj = ^j (v1,..., v^) = |BjI — kj(d + 1) при j Е 11,..., 2^d| ,                 (1)

где wj (d + 1), j Е {1,..., 2^d}, определяются рекуррентно:

w1(2) = ап, w2 (2) = ^п,

FFi ^{+ 1)} = [^аҒк^(г)], "'2k^{(г + 1)}    "i^{(г) —} [^аҒк^(г)], ^{к Е} {^1,...^,2г-1}^{,г Е {1,}...^,d}.

Здесь и далее [•] обозначает целую часть числа (с округлением в меньшую сторону).

Обозначим V^d міюжеетво всех d-последователыіостей вершин из V. для которых \xj I 6 f (п), j Е {1,..., 2^d}. Будем говорить, что остовный подграф G² дистанционного графа. G обладает свойством Ext^di^st(R, Н). если для любого (v¹,..., v^d) Е V^d найдутся такие w¹,..., w^k Е V \{v1,..., v^d}. что {z₂,yj } Е Е (Н) ^ {v², w^j} Е E(G~) для любых г Е {1,...,d}. j Е {1,...,к} іі {уі ,Pj } Е Е(Н ) ^ {w², w^j} Е Е (G²) для любых i,j Е {1,...,к}. ііііыміі слов; іміі. свойство Ext^di^st(R, Н) получается ітз Ext(R, Н) рассмотрением только тех d-послелователыюстей вершин из V. которые принадлежит V^d. Таким образом, нас интересуют только последовательности вершин, разбивающие {1,...,п} на части, приблизительно равные tej(d + 1), j Е {1,..., 2^d}. Теорема, сформулированная ниже, выполнена при условии f ^ п^2/3 и является обобщением соответствующей теоремы из [10] на случай произвольного а.

Теорема 6. Пусть с₁ есть число авто морфизмов графа Н, которые оставляют на месте каждый корень х_г Е R. Пусть р = р(п) удовлетворяет равенству

N k

(N >

р¹ /c₁ = d ln N.

Тогда р является точной пороговой вероятностью для свойства Extd^lst(R, Н).

С точностью до используемых вспомогательных утверждений теоремы 4-6 доказываются так же, как и в случае а = 1/2, рассмотренном в [10]. Эти сформулированные в п. 2.2 утверждения, интересные и сами по себе, в случае произвольного а требуют другого подхода. В силу схожести доказательств лемм со случаем а = 1/2, мы ограничимся доказательством только первой из них в разделе 3, детали которого достаточно сильно отличаются в случае произвольного а.

2.2.    Формулировки основных лемм

Пусть J(п) — произвольная последовательность положительных чисел, причем ф ^ п^2/3. Пусть, кроме того, (R, Н ) — произвольная сеть с V(Н ) = {z1, ..., Zd,y1,..., yk }, R = {z₁, ..., Zd} и e(R, Н ) = I. Для раз личных v¹,..., v^d Е V обозначим M ( r, _h ) (v¹,..., v^d) количество инъективных отображений из V (Н ) в V, переводящих z^ в v¹, г Е {1,...,d}, и сохраняющих ребра между вершинами, среди которых хотя бы одна не является корнем. Поскольку величина M ( r,h )(v¹,..., v^d) ^не зависит от выбора конкретных вершин, а лишь от значений \Bj | (см. пара граф 2.1), j Е {1,..., 2^d}, которые, в свою очередь, зависят только от чисел х₁, ... ,х₂у будем обозначать M (_R h ) = M ( r,h )(v¹,•••, v^d) ^гД^е вектор х := (х₁, ..., х ₂< ) определен в (1).

Лемма 1. Найдется такая функция M(rh) = M(rh)(п), не зависящая х от х. что с условием

M ^ ^rh ) = M(’RH) (1 + 0 ((/(п))³/п²)) при п ^ то равномерно по всем х |Х1 6 ^{ф (п) j Е {1},..., 2^d}-

В следующем утверждении была получена асимптотика числа вхождений произвольного графа F в дистанционный граф G, которая выражается таким же образом, как и в случае а = 1/2.

Лемма 2. Пусть Mp — количество мономорфизмов графа F с к вершинами и Г ребрами о G. Тогда

M_p ~ M(к, Г) := N^k

(У

Как и в случае а = 1/2, мы получили формулу для M^rh ) из леммы 1.

Лемма 3. В обозначениях леммы 1 в качестве M ( r н) можно выбрать M(к, Г)

Доказательства последних двух лемм проходят так же, как в случае а = 1/2, отличаясь лишь использованием вспомогательных утверждений настоящей статьи. Поэтому здесь мы их не приводим.

3.    Доказательства лемм

В пи. 3.1-3.2 мы введем дополнительные обозначения и сформулируем и докажем некоторые вспомогательные утверждения. В и. 3.3 будет доказана лемма 1, сформулированная в предыдущем разделе.

3.1. Дополнительные определения и предварительные замечания

В дальнейших рассуждениях нам понадобятся вспомогательные обозначения. Пусть (R, Н) — произвольная сеть с V(Н) = {z1,..., zd, y1,..., yk}, R = {z1,..., zd} и e(R, H) = Z, a v1,..., vd G V — произвольные различные вершины. В обозначениях из раздела 2 положим to?(1) = iuKd + 1) + x1,..., х^(1) = чу^d(d + 1) + x2d.

Рассмотрим произвольное s G {1,..., к} и такие различные вершины w1,..., ws G V, что {Zi,yj} G E(H) ^ {v%w3} G E(G) для лтобых г G {1,...,d}. j G {1,...,s} и {Уг,Уз} G E(H) ^ {w\ w3} G E(G) для лтобых i,j G {1,...,s}. Для вершин v1,..., vd, w1,..., ws-i рассмотрим разбпение множества {1,...,п} на подмножества Bi,... , В2d+s-i (см. раздел 2), мощности которых, как несложно видеть, зависят от чисел x1,..., x^d. II положим to =wf(s) = |Вз|, Bj = {г3 ,...,ЕШ.}, j G {1,..., 2d+s-1} .

Посмотрим теперь на вершину w^s и на ее координаты как вектора в V. Для каждого j G {1,..., 2^d+s-1} обозначим n?(s) количество единиц среди чисел ит^ ,..., w^sj

3                                                                   rL.

(мы обозначили w^, ...,ш(( координаты w^s). В силу определения дистанционного графа G(n, ап, а²п) ясно, что наличие ре бра между вершиной w^s іі пекотороіі вершиной v из v¹,..., v^d, w¹,..., w^s-1, представляется в виде равенства скалярного произведения этих вершин а²п. Последнее, в свою очередь, единственным образом записывается в виде суммы 2^d+s-2 _{величин} u^s) с единичными коэффициентами (где индексы входящих в выражение величин суть индексы множеств Bj, для которых координаты вершины v с номерами из Bj равиы 1). Кроме того, для вершины w^s справедлив!) равенство (w^s, w^s) = ап. Этот скалярный квадрат, очевидно, записывается в виде суммы всех njj(s), j G {1,..., 2^d+s-1}.

Предположим, что в графе Н среди вершин Х1,..., xd, У1, ..., y_s-1 только вершины

^xZ1(s),...' ^xl¹, ,(s),^yll(s), ^{. .}

1                    ^a(^s)          1

. ,У/2 (s) соединены рсбрамн с вершиной ys (здось a(s) — коли-L b(s)

чество вершин среди х₁, ... ,xd, соединенных с y_s, b(s) — среди y₁, ..., y_s-1). Обозначим с^(1,г), ^{г G} ФУ),... У^)}, и с^(2,г), г ^G {Z^),.. .^,lb(_s)^(s )}, последовательности индексов —

переменных uj-(s), входящих в уравнения, соответствующие наличию ребер между вершинами ys и xi, г G {Z¹(s),..., Z¹(_s)(s)}, и между вершинами ys и у», г G {Z²(s),..., Z2_(s) (s)}, соответственно. Заметим, что длины всех таких последовательностей совпадают и равны m(s) = 2^d+s-2. Тогда для того, чтобы вершина w^s была соединена с вершинами

vl1(s),..., vll(s)(s), wl2(s),..., wl2(s)(s), равенства и неравенства системы

необходимо и достаточно, чтобы были справедливы

^              ^

"Z1(1,l1(.))

п^

C1 (_1’l«(s)(s))

ПТ

C1(2,ll(s))

...

(s)+ . .. +ПЖ z         (s)=a2n,

Cm(s) (1,la(s) (s))

' + П?„.)(2,І$(.))(*) = а2”-

Очевидно,

...

^                ^

-ж / 2      \ (s) + ... + пж     , 2      \ (s) = a2r

C1 (2,lb(s) (s))                       cm(s) (2’lb(s) (s))

n₁(s) + n₂(s) + ... + n₂d+s-1 (s) = ап, ^{k                       k}

Vj G {1, 2, 3,..., 2^d+s-1} 0 6 n^s) 6 w^s).

— m1rh . = V с и—(1)... cu—(1)

(R.H)    z^ _w?(1) _w^d(1)

— u^(k)      x-,U2d+fe-1 (k)

c —   ... c —        ,

№l(k)        №2d+fc-1(k)

—— где суммирование в выражении ведется по всем решениям (п.(1),..., пД (1)), ..., ——

(uf(k),..., u’,_d+k-1 (к)) систем (2) с s =   1,...,s   = к соответственно. Здесь

—             —    —           —— ш.— (s + 1) = n.(s), шД (s + 1) = ш.Д) - u.(s) при любых s Е {1,...,к —1},

3 Е {1,..., 2^d+s-1}.

3.2.    Вспомогательные утверждения

В предложениях ниже будем предполагать, что функция f (п) такова, что п¹/² ^ f (п) ^ п^2/3.

Предложение 1. Пусть

Ғ(ші, Ш2,X,t) =

С [аиД+^С [аиД-.+І

[awt]  [aw2]

Cwi  ^W2

Пусть таксисе для постоянных 0 < с,С <  1 выполнено сп 6 шг 6 Сп, г = 1, 2. Кроме того, пусть ші + ш, = ш. сп 6 ш 6 Сп. Тогда при достаточно больших п для некоторых' (зависящих от а) положительных констант СуС,

Ғ(wi,W2,x,t) 6 Сіе^{1 ln}^^/a) При |t| 6 f (п) и любых’ x.

Ғ(wi,W2,x,t) 6 Сіе^{1 ln(}№^)-C2⁽f И^)2/и при |t| 6 f (п) Z I |x| >  f (п).

Доказательство. Будем предполагать, что |t| 6 f (п). Пусть сна чала также |x| 6 f (п). Легко видеть, что

СД = . /           exp ( Н ( ^т) п + О (--1-- ) ) . т ^ ж,п — т ^ то.

у 2кт(п — т)        п )     —п  п — т

Используя это асимптотическое равенство и раскладывая Н (•) по формуле Тейлора, получим, что

^^С   ■ ' = ^==й!==. exp (^НМШ1 +

^[аш1]-^ ^{+ x} 1        [^аші]-^аші ^{+ x} V       /^{(f (п))3} \

^{+Н (а)}------ші------^{ші +} 2^{Н (а)} (------ші------ ш ^{1 + 0} ) ) ^Х

2я([аш2]

ш2

— x + t)(ш₂ — [аш₂] + x — t)

exp

Н Н (а)ш2+

+ Н ‘(а)\"^шl-mшl—x±l ш2 + 1Н ‘‘(а) ([ашгіхяшіхяхі ^’ш, + О ш2              2                ш,        /

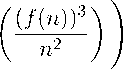
1  /                 шіш,

^Н (а)ш+

2л у [аш1][аш2](ш1 — [аш1])(ш2 — [аш2]) Р

Р                                     1 (x²    (x — t)²          (f (п))³

⁺ in (^а j^{([аші] + [аш,] — аш +1)} — тар (ші⁺        )^{+ О}          ).

Здесь мы учли, что Н ‘(x) = ln((1 — x)/x) и Н"(x) = — .(і—.) • Таким образом, Ғ(ш1,Ш2,x,t) 6 Сіе^{1 ln(}P^/a) ири |x| 6 f (п) (с обозначенными выше условиями на ші,ш,).

Кроме того, Ғ(ш₁,ш₂,x,t') 6 С₁е^{1 lnL(}d/“^)-C2⁽f (и))²/» _Пр_и |x| = [f(п)]. Для того чтобы получить утверждение, покажем, что, начиная с некоторого п, величина Ғ (ші,ш,,x,t) при

|t| 6 /(п) монотонно убывает по ж при ж > [/(п)] и монотонно возрастает при ж 6 — [/(п)]:

F(w1, w2, ж + 1, t)        ([aw1] + ж)!(гУ1 — [aw1] — ж)!

F(w₁, w₂, ж, t)      ([awi] + ж + 1)!(w₁ — [aw₁] — ж — 1)

([aw2] — ж + t)!(w2 — [aw2] + ж — t)!

([aw2] — ж — 1 + t)!(w2 — [aw2] + ж + 1 — t)

(a — ж)(Ь — ж + t)               ab — (a + Ь)ж + ж² + t(a — ж)

(с + ж + 1)(d + ж + 1 — t)    cd + (с + d')(ж + 1) + (ж + 1)² — t(c + ж + 1)

= 1 +

(ab — cd) — (a + Ь + с + d)ж — (с + d) — 2ж — 1 + t(a + с + 1) cd + (с + d)(ж + 1) + (ж + 1)2 — t(c + ж + 1)

—wж + w11 + О(п)

(с + ж + 1)(d + ж + 1 — t)

О(п) — wж + O(n)+w1t + О(/(п)) (с + ж + 1)(d + ж + 1 — t)

Здесв a = w1 — [aw1],  b = [aw2], с = [aw1],   d = w2 — [aw2].

Отсюда при достаточно больших п

F(W1, W2,Ж + 1,t)

F (W1,W2,Ж,t)

< 1. ос ли ж > [/ (п)].

и

F(w1, W2,ж + 1,t)

F(W1, W2,ж,t)

> 1. если ж 6 — [/(п)].

Предложение доказано.

Предложение 2. Пусть v ¹ = v ¹(n),..., v ¹ = v ¹(n) — вершины графа G, разбивающие множество {1,..., п} на подмножества В₁,..., B₂i мощностей ш₁(г + 1),...,w₂; (г + 1), причем при достаточно больших п для любого j G {1,..., 2¹} выполнено сп 6 wj (г + 1) 6 Сп, г де 0 < с, С < 1 — некоторые положительные постоянные. Выберем вершину с номером г + 1, фиксируя в каждом подмножестве Uj (г + 1) позиций, для которых соответствующие координаты искомой вершины-вектора равны 1, при чем ^ 2=14? (г + 1) = ап. Множество таких вершин, отвечающих набору и(г + 1) = (U1 (г + 1),..., u₂t (г + 1)). будем, обозначать V_u(_i+₁)( v ¹,..., v¹). Тогда, если хотя бы для одного j из {1,..., 2¹} выполнено |uj (г + 1) — [awj (г + 1)]| > / (п), то при достаточно больших' п мошдост/ь мнозісества. V_u(_i+₁)( v ¹,..., v¹) не превосходит С₁е^н(a)n-C2⁽f О)) ^/п для некоторых положительных констант С₁,С₂.

Доказательство. Заметим сначала, что

ІТ/ . . Л 1 _vill — <ч«1⁽¹+¹⁾ ^Х^^{1 (1+1)} I Pup+p l^v , . . . , ^v 11 = ^Сш₁(г+1) . . . ^С_№^ (i+1).

Будем доказывать утверждение по индукции. Пусть г = 1. Представляя Uj(2) = awj(2) + tj (2). j G {1,2}. получаем. что t₁(2) = ж = —1₂(2). Поэтому количество способов выбрать вершину с |t1(2)| > /(п) (и, соответственно, с таким же условием на. ^2(2)) в силу предложения 1 не превосходит С1е^н(а)п-С2⁽Т (Д) ^/п.

Предположим, что предложение доказано для всех г 6 р — 1, докажем его для г = ц. Пусть для некоторого k G {1,..., 2^-1} выполнено |u2fc-1(p + 1) + U2k(р + 1) — [aw2fc-1(p + 1)] — [aw2fe(ц + 1)]| > /(п). Образуем вектор п‘(ц) = (п‘1(д),... ,U‘2M-1 (ц)) по правилу п^(ц) = Н2к-1(ц + 1) + U2k(р + 1), k G {1,..., 2^-1}. Рассмотрим первые ц — 1 вершин и множество ^‘(^(v1,..., v^-1) вершин графа G. отвенаютних набору п‘(ц). Заметим, что Pu‘(^)(v1,..., v^-1) нс завііснт от v^ ii VU(д+i)(vi,...,vM) С Vu‘(и) (v1,..., v^ 1)- Поскольку л. тя некоторого k G {1,..., 2^ 1} выполнено |uk(ц) — [awk(ц)]| > /(п) — С1 С1 = const > 0. где wk(ц) = W2k-1(ц + 1)+w2k(ц + 1)- по предположению индукции Д/Д’^^) (v1,... , vAt-1)| < C1eH(“)Tl-C2(fW)'2/— a следовательно, | V^+^v1,..., vM)| < C1eH(a)n-C2(f(n)1)2/n. Здесь C1, C2. как и раньше. — некоторые положительные константы.

Таким образом, можно далее считать, что для всех k Е {1,..., 2^^-1} выполнено |«2k-1(p + 1) + ^2к(ц + 1) - \aw2k-1(p + 1)] - \aw2k(ц + 1)]| 6 /(и). Представим н , (ц + 1) в следующем виде:

Н2к-1(ц + 1) = \а^2к-1(ц + 1)] + qk (ц + 1),

^H2k ⁽Ц ⁺ 1) = \ttW2k ⁽Ц ^{+ 1)] — q}k ⁽Ц ⁺ 1) ^{+ S}k ⁽Ц ⁺ 1).

Ясно, что для всех к Е {1,..., 2^^-1} выполнено |sk (ц + 1)| 6 /(и). Поэтому можно применить предложение 1 для соответствующих пар последовательных множителей в выражении Для ^|V_и(_м+1)^(v1,...^, v^ )|:

|V_u(^₊₁₎(v¹,...,v^M)| 6 C₁e^k=-1 ^H(»WW^²k=i з^УМУИ—ОД (ⁿ))^2/n       ^

Поскольку

2''

^2 Hj (ц + 1) = an, j=1

выполнено

2^-1

£ s , (p + 1) = 0(1).

j=1

Таким образом, последнее выражение в (4) не превосходит (A₁e^H(a)n-C2(f (Д)²/— _Гд_е C^C₂ — некоторые положительные постоянные.

Предложение доказано.

3.3.    Доказательство леммы 1

Без ограничения общности будем считать, что / ^ и0'6. Будем также предполагать, что / (и) > и0'6 при всех и.

Доказательство проходит по той же схеме, что и в случае, разобранном в [10]. Для полноты картины мы, как и в [10], сначала обозначим основные идеи доказательства, а затем все строго докажем, не ссылаясь на доказательство соответствующей леммы из [10].

Идея доказательства. В разделе 3.1 мы свели задачу нахождения числа расширений M (^rh ) ^{к П0ИСК}У асимптотики для некоторой суммы (3) по решениям к систем уравнений (2). В такой формулировке достаточно доказать, что эта асимптотика не зависит от Ж1,..., x₂d и равномерна по ним при |жг | 6 J (и), г Е {1,..., 2^д}. —       —

Как будет видно далее, максимум суммы (3) достигается при uj-(s) = \awj(s)] +0(1), и ^ то. Также будет показано, что если в сумме (3) проводить суммирование не по всем — uHs), удовлетворяющим соответствующим системам уравнений (2), а лишь по таким, что --

|uj(s) — \awj:(s)]| 6 и0'6, то асимптотика суммы не поменяется, причем сохранится и равномерность по Ж1,..., X2d (при достаточно малых ж). Для такой «укороченной» суммы уже гораздо легче, вводя для удобства новые переменные и обозначения, доказать равномер ность ее асимптотики.

Доказательство. В силу определения чисел ж₁,..., x₂d существуют та кая константа с > 0 II такие d целых чисел ац..., ад. что |a j | 6 с для всех j Е {1,..., d} и всктор (ж1,..., X2d ) является решением системы (2), в которой s = 1, а(1) = d и правая часть заменена на столбец (ац..., ад, 0)^т. Покажем, что существует такая константа C >  0, не зависящая от (ж₁,..., x₂d ), что для всех j Е {1,..., 2^д} найдутся числа у , = у , (и) Е Z и г , Е Z,

для которых

7 = «2 dj ^{+ r}j ,

а вектор (yi,... ,y₂d ) является решением сіістемы (2). в которой s = 1. а(1) = d и правая часть заменена на столбец (0,..., 0)^т. Обозначим последнюю систему следующим образом:

Ay = 0. Подставив вместо у век тор (|Ч1/«2 ],.

.

., [a^d/«2]) получим в правой части некото-

рый вектор (bi,..., bd+1)T, абсолютное значение каждого элемента которого не превосходит некоторой константы с > 0. Заметим, что для любого г Е {1,..., d +1} в г-ой строке матрицы A = (ai,j)d+1 содержится ненулевой коэффициент: ai,2d-2d-i = 1 (если г Е {1,..., d}) и °d+i 2d = 1) ПРИ этом соответствующие коэффициенты в остальных строках (кроме последней) равны нулю: aj,2d-2d-i = 0 (если г Е {1,..., d}, j Е {1,..., г — 1, г + 1,..., d}) и aj,2d = 0 (если j Е {1,..., d}). Следовательно, положив d2d-2d-i = X2dJd *] — bi ПРи г Е {1,..., d}, y2d = [ Д'1 + ^ bi — bd+1, 1 «2 J І=1

^y = [|] -рп,-^Е {1,.

.

., 2d} \ pd — 2d-i, 2d

—

2d-2,...,2d — 1, 2d} ,

мы получим искомый вектор у.

Введем для удобства новые обозначения:

^tj ^(s) = ⁿ-^{(s) —} [« (^w-^{(s) — E}j ^(s)) ] ,

где Ej (1) = rj при j Е {1,.

.

., 2^d}. а при s Е {2,..., k}

/ Гу , если j = 2^s 1q. q Е {1,..., 2^d}: ^E3 ^(s) =

0, иначе.

Кроме того, пусть в обозначениях раздела 2 wj(1) = wj (d + 1), j Е {1,.

.

nj (s) пр и s Е {1,...,k}, j Е {1,.

.

., 2^d+s 1} _п wj(s) щэй s Е {2,..., k}. j Е {1,.

., 2d}. Далее.

.

.,2d+s-1}

определяются из следующих рекуррентных соотношений:

nj (s) = [«wj (s)] + tj (s),

^w2 j-i ^(s)=ⁿj^{(s —} 1),   ^w2 j ^(s) = ^wj^{(s —} 1)

--

— nj (s — 1),   j Е {1,..., 2d+s-2} .

-

Очевидно, wj? (1)  = wj(1) + «₂dj + rj и nj(1)  =  [«wj(1)] + «і«₂~^ + tj (1)

^{j Е {1},.

.

--

., 2^d}. Получим no индукции аналогичные выражения для wj-(s) 11 njj(s)

при при

s Е {2, ...,k}, j Е {1,..., 2^d+s 1}. Пусть s Е {2,..., k}. Предположим, что для любого j Е {1,..., 2^d+(s-1)-1} справедливы равенства

—

—

wj(s — 1) = wj(s —1)+ 6j (s —1) + Ej (s —1), uj-(s — 1) = [«wj(s — 1)]+«ф-(s —1) + tj(s — 1), (10)

где 5j (s), s Е {1,..., k}, j Е {1,..., 2^d+s 1}, определяются из рекуррентных соотношений:

6j (1) = «^ yj , j Е {1,..., 2^d} ,

^2j-1^(s) = «6j ^{(s —} 1), §2j ^(s) = P^j ^{(s —} 1), ^{j Е} {1, . . . , 2^{d+s 2}| .

Тогда в силу (8), (9) и (10) для любого j Е {1,.

.

., 2d+(s-1)-1} имеем

—

—

—

W2j-1(s) — Uj (s — 1) — Uj (s — 1) + a5j (s — 1) — W2j _— 1(s) + ^2j-1(s),

—

w^jj (s) = wj(s -

1) - u—(s - 1) = wj (s - 1) - uj (s - 1) + 3§j (s - 1) + Ej (s - 1) =

= w2j (s) + §2j (s) + E2j (s).

Окончательно, для любого j Е {1,.

.

. , 2^d+s 1} выполнено

-

Wj (s) = Wj (s) + 5 j (s) + Ej (s).

(И)

Следовательно, в силу (7)

uj(s) = tj (s) + [a ^wj(s) - Ej (s)^ = [awj] + adj (s) + tj (s).

Таким образом,

-

M(R,H)

__         [awl(1)]+ad1(1)+*1(1)     /<-<[aW2d(1)]+ad2d(1)+t2d(1)

=     Gw‘(1)+5i(1)+ei(1)     . . . Gw2d(1)+52d(1)+e2d(1)      X ... X

_С[awl (k)] +a6i(k)+ti(k)    _С [^aw2d+k-1 W] ^+a^d+k-1 to+Cd+fc-1 ^(k)

^X  wl (k)+8i(k)+ei(k)      ^...   w'_2d+_k-1 (k)+82d+k-i (k)+e2d+k-i (k)      ,

где суммирование ведется по всем наборам (t1(1),..., t2d(1),..., t1(k),..., t2d+k-i(k)), таким - что числа и3- (s), s Е {1,..., k}, j Е {1,..., 2d+s-1}, определяемые равенством (7), являются решением систем (2) при s Е {1,..., k}.

Докажем, что суммирование в (13) можно осуществлять по некоторому такому множеству T = T (п) наборов (t1(1),..., t2d(1),..., t1(k), ..., t₂»+k-i (k)). не зависящему от $1,...,^2d, что равенство в (13) заменится на асимптотическое равенство и для всех  (t1(1),..., t₂d (1),. ..,t1 (k),..., t₂d+k-i (k))  Е T будет вгтпо.тпепо  |tj (s) |  6  п⁰-⁶  при

s Е{1,...,k}. j Е {1,..., 2^d+s-1}.

Заметим, что в силу определения вектора    (у1 ,...,y₂d )

(51(1),..., 5₂d (1)) = (y1,...,y₂d ) является решением системы (2), в которой

вектор s = 1,

а(1) = d и правая часть заменена на столбец (0,. -

.

., 0)т. Произведем замену переменных

u^j(1), j Е {1,..., 2^d}, в системе (2) в соответствии с (12). Тогда коэффициенты системы при s = 1 без ограничений, записанных в ее последней строке, не зависят от ж. Следовательно, и ее решения также не зависят от ж. Более того, при достаточно больших п любое решение (t1(1),..., t2d(1)) системы (2) при s = 1 без ограничений, записанных в ее последней строке, удовлетворяющее неравенствам |tj (1)| 6 п^0-6, j Е {1,..., 2^d}, удовлетворяет этим ограничениям, так как w^j(1) > [(min{a,^ })^dп] - J (п) при всех j Е {1,..., 2^d}. Следовательно, множество всех наборов (t1 (1),..., t₂d(1)), удовлетворяющих неравенствам |tj (1)| 6 п^0-6, j Е {1,..., 2^d}, и определяемых равенством (7), совпадает с множеством всех наборов (t1(1),..., t₂d (1)). удовлетворятощих неравенствам |tj(1)| 6 п^0-6. j Е {1,..., 2^d}. ii являющихся решениями системы (2) без ограничений, записанных в ее последней строке. Обозначим T(1) множество всех таких наборов. Заметим, наконец, что в силу (6), (8),

(9) и (11) для любого набора (t1(1),..., t₂d (1)) Е T (1)

выполнены неравенства

- wj(2) > wj (2) - С1 /(п) > [min{a,^}wj(1)] - п0- -

С1/(п) >

> ^(min{a,^})d+1п] - С(2)/(п)

при всех j Е {1,..., 2^d+1}, г де С1 и С (2) — некоторые положительные константы.

Пусть s Е      {2,...,k}    и множество     Т (s — 1) наборов

(t1(1),..., t2d(1),..., ti(s — 1),..., t2d+s-2(s — 1)) задано. Рассмотрим произвольный набор t = (ti(1), ...,t2d(1),...,ti(s — 1),...,t2d+s-2(s — 1)) Е Т(s — 1).

Пусть для всех j Е {1,..., 2d+s-1} выполнено w—(s) > [(min{a,/3})d+s 1n] — C(s)/(n),

...

где C(s) = const > 0. По аналоги!i co случаем s = 1 в силу определения вектора (y1,

,^2d )

вектор (^i(s), . . . , d2d+s-l(s)) является решением ciістемы (2). в которой a(s) = d. b(s) = s — 1 — и правая часть заменена на столбец (0,..., 0)т. Снова сделаем замену переменных uj(s), j Е {1,..., 2d+s-1}. в соответствии с (12). Поскольку коэффициенты системы без ограничений, записанных в ее последней строке, не зависят от — и являются функциями от переменных tj (г), j Е {1,..., 2д+г-1}, г Е {1,...,s — 1}, которые также не зависят от —. то II решения такой <шетемы не зависят от —. и при достаточно больших n любое решение (t1(s),..., t2d+=-i(s)) системы (2) без ограничений, записанных в ее последней строке, удовлетворяющее неравенствам |tj (s)| 6 n0'6, j Е {1,..., 2ci+s-1}, удовлетворяет этим ограничениям в силу предположения (14). Следовательно, множество всех наборов (t1(s),..., t2d+=-i (s)), удовлетворяют, их неравенствам |tj (s)| 6 n0'6, j Е {1,..., 2ci+s-1}, и определяемых равенством (7), совпадает с множеством всех наборов (t1(s),..., t2d+=-i(1)), удовлетворяющих неравенствам |tj(s)| 6 n0'6, j Е {1,..., 2d+s-1}, и являющихся решениями системы (2) без ограничений, записанных в ее последней строке. Обозначим Т(t) множество всех таких наборов. При s < k, j Е {1,..., 2d+s} и лкобом (t1(s),..., t2d+s-i(s)) Е Т(t) в силу (6), (8), (9), (11) и предположения (14) имеем

— wj (s + 1) > wj(s + 1) — C1 /(n) > [min{a, ^}wj (s)] — n0' — C1/ (n) >

> ^min{a,^} (w—(s) — 6j (s) — Ej (s)}] — C2/(n) > [(min{a,j9})^d+sn| — C(s + 1)/(n), где C₁,C₂,C(s + 1) — положительные константы. Положим

Т^) =                  U                 {t}x Т^).

t=(ti(1),''',t2d (1),''',ti(s-1),''',t2d+s-2 (s-1))GT(s-1)

Множество Т определим следующим образом: Т = Т(k). Осталось доказать, что равенство в (13) заменится на асимптотическое равенство при суммировании по всем наборам из Т.

По аналогии с доказательством существования чисел y1,...,y₂^d> для которых выполнено (5) и (6), можно доказать, что для любых —1,...,—2d существует такое число с = const > 0. нс зависящее от —. и и;кбор (t₁ (1),...,t₂d (1),..., t₁(k),..., t₂d+k-i (k)) Е Т. что выполнены неравенства tj (s) 6 с для всех s Е {1,...,k}, j Е {1,..., 2^d+s-1}. Соответствующий этому набору элемент суммы из правой части равенства (13), как будет следовать из (16), оценивается снизу величиной е^{н (a)n}/n^c для некоторой константы с > 0.

Заметим, что в силу (14) найдется такое с > 0, что для всех —1,..., —2d Е [—/(n), /(n)], (t1(1),...,t2d (1),...,t1(k),...,t2d+fe-i (k)) Е Т. s Е {1,...,k} 11 j Е {1,..., 2d+s-1} — при достаточно больших n выполнено cn 6 wj^s) 6 n. Поэтому можно применить предложение 2, откуда следует, что слагаемые в (13), соответствующие наборам ((t1(1),..., t2d(1),..., t1(k),..., t2d+k-i(k))). в которых xoтя бы одно из tj(г) удовлетворяет неравенству |tj(г) | > n0'6, дают в совокупности nfc2d+fe-1 e-Q(n°.2)eH(a)fen

= о е^^{1 (a)kn}/n^ .

Здесь g(n) = Q(^(n)) означает, что при достаточно больших n для некоторого С >  0 выполнено g(n) >  Сһ(п). Окончательно получаем

—    =                ^                 [аД(1)]+а81(1)+Ц(1)

(F^H)                      / j                  ^w‘(1)+8i(1)+ei(1)

(ti(1),...,t2d (1),...,ti(k),...,t2d+k-i (k))ET

.

.. х

[^aw2 _d ⁽¹⁾] ^+a82d ^(1)+t₂d ⁽¹⁾        [awl (k)] +a81 (k')+t1(k)

^{X   w}2 _d(1)+82d (1)+e₂d(1)      . . .   w1 (k)+8i(k)+ei(k)

.

.. х

Д “^W2 d+k-1 '' ^a82././   (^k)+t₂d₊k-1 ^(k) A       /1 \\

^{X   w}2 d+k-1 ^(k)+82d+k-1 ⁽k⁾⁺e₂d+k-1^(k)      (^   ^{+ 0} Уп) )

равномерно по всем x₁ , ...,x₂d E [-/(n), /(n)]. Покажем теперь, что

_С [awl (s)]+a»l(s)+t1(s) _С ^aw' d+s-1 ⁽ⁱ⁾] ^+a82d+s-1 ^(s)+4d+s-1 ^(s) w‘(s)+8i(s)+ei(s)      . . .   w2_d+_s-1 (s)+82d+_s-1 (s)+e₂d+s-i (s)

~

[aw‘(s)]+ti(s)        [a£d+s-1(s)] +t2d+s-1(s)

~ Cw‘ (s)           •••Gw'., .(s)

2d+s-

равномерно по всем x₁,...,x₂d E [-/ (n),/ (n)], s E {1,...,k} и (t₁(1),..., t₂d (1),..., t₁(k),..., t₂d+k- 1(^)) E T. у

Поскольку в силу (14) для всех s E {1,...,k} ид E {1,..., 2^d+s-1} выполнено wj(s) > cn для некоторого c > 0, по формуле Стирлинга найдется такая константа с > 0, что для всех тех же наборов переменных

[^aW^(s)]^+a8_d ⁽s)+tj (s) / [а£^(s)]^+a8_d ^(s)+tj (s)             (s)

Д (s)+8j(sHy (s)    / ^Cw< (s)+8j (s)               P

<5 M

.

n

Более того, по формуле Стирлинга существует такое М > 0, что для всех w E [cn, n] П N имеем

!   -1 6 М.

V2TT у     w

Разложение Тейлора дает существование такого ci > 0, что для всех s E {1,...,k}, w E [cn,n], |y| 6 /(n)

Vw - 1 6 _c I У I 6 ci ^ ^{/ (n)} Vw + у          I w I c n

Заметим, что в силу определения величин xi,...,x₂d и yi,...,y₂d справедливы равенства £2=1 х- = £2=1 у. = 0. а. слелователвио. £^₌₁ ^д = 0 в силу (6) и £²=Т-¹ 6₃ (s) = ^£2!+^{- 1} Е₃ (s) = 0 для лтобого s E {1,...,k} в силу определения величин 6₃ (s) 11 е₃ (s). Наконец.

[aw< (s)]+a83- (s)+tj(s) = w'j (s)+8j(s)             —

^wg^(s) + ⁵j ^(s)

^ 2л ^[aw<(s)] +a5₃ (s) + t.(s)^ ^w' (s) - ^aw' (s)j + P^j(s) - t.(s)^

X

awj (s) - aw'(s) + t₃ (s)

X exp H(a) (wj(s) + 63(s)) + H'(a)-^-----Д77ДГГТ7Д-------(wJ(s) + 5j(s)) + у                                          w3(s) + °j(s)

- aw''(s) + t₃ (s) ’ 3<^{s) +} °3 ^(s)

+ 2 Я "(a)

J2та,ЗМЫ exP (Н^Ү(8) +Н(“)(Л ““/8) + ti(8)) + !        ([aw' (8)] -aw' (8) + t, (8))2      ((/(„))3 Л + 2Н (a)            w' (8)             ' " t »2 И - = 6H(«)«,(s)c[«w;<")l+t.И Д + " ((ЛСД))3)) wj(s)                           n2 равномерно по всем Ti,...,^ € [-/(»),/ (»)], 8 € {1,...,k}, 3 € {1,..., 2,;'s 1} и (ti(1),...,t2d(1), ...,ti(k),...,t2d+k-i(k)) € Т.

Поэтому

„ [aw! tol+a^i

w1 (s)+<5i(s)+ei(s)      . . . ^w^d+s-1 (s)+<52d+s — i (s)+e2d+s-i (s)

— ^2=+= 1   (s)   [awl(s)]+a5i(s)+ti(s)

. . X

w( (s)+5i (s)

aw xd, 2d+ w '

2d+s

■ s

-

—1 (s)] +a^2d+s-1 (s)+^2d+s-1 (s) (s)+^2d+s-1 (s)

(1 + "V »"))-

H(a) E^T- 5j (s)J«w‘(s)] +ti(s)       [^aw2d+s-1^(s)] ^d+s-1^(s)

(1+" ()) -

• ⁶                   ^(s)         ...^Gw2d+s-i (s)

_ [awi (s)] +ti (s)     ^ [^aw2d+s-1^(s)] ^+t2d+s-1^(s)

(1+" ())

w' (s)               .. . w'         (s)

1                         2d+s-1

равномерно по всем x1,...,x₂d € [—/(n),/(n)], 8 € {1,...,k} и (ti (1),...,t₂d(1),..., ti(k),..., t2d+k-i (k)) € Т. Тем самым лемма показана, поскольку множество Т и все величины в правой части не зависят от х.

Работа выполнена при финансовой поддержке гранта РФФИ 15-01-03530.