Маневренное испытание "зигзаг" и обученная нейросеть как инструменты идентификации адекватной математической модели движения судна

Пашенцев С. В. и др. Маневренное испытание "зигзаг" и обученная нейросеть как инструменты идентификации адекватной математической модели движения судна. Вестник МГТУ. 2025. Т. 28, № 4/1. С. 558–571. DOI:

e-mail: , ORCID:

Pashentsev, S. V. 2025. Zigzag maneuvering test and trained neural network as tools for adequate identification of the mathematical model of vessel motion. Vestnik of MSTU, 28(4/1), pp. 558–571. (In Russ.) DOI:

Нейронные сети широко используются при решении разнообразных прикладных задач: распознавание образов, классификация, кластеризация, прогнозирование временных рядов ( Николенко и др. 2018 ); реже – задач регрессионного типа в многомерном пространстве. Предыдущие работы по данной тематике ( Пашенцев, 2023; Юдин и др., 2024 ) касались проблем связи параметров математической модели движения судна с характеристиками управляемости, полученными в процессе компьютерных испытаний модели. В ходе решения задач с помощью пакета Statistica Neural Nets (SNN) доказано достоверное предсказание характеристик управляемости по параметрам математической модели судна, выполненной обученной нейросетью ( Пашенцев, 2023 ). Решение задачи регрессии от параметров модели к характеристикам управляемости не рекомендовалось для практического применения и было выбрано при разработке нового подхода. Для целей коррекции математической модели следует решать задачи обратной регрессии – от характеристик управляемости к параметрам корректируемой модели, повышая таким способом ее адекватность.

В работе ( Юдин и др., 2024 ) показана инверсия входа и выхода сети; увеличено число характеристик управляемости судна до 20; число параметров математической модели движения увеличено до 19 и включало массы корпуса судна и момент инерции. Задача регрессии с переходом от 20 к 19 переменным составляет вполне приемлемое соотношение между входом и выходом. В работе использован иной способ генерации наборов для обучения сети: равномерно распределенная вариация параметров модели изменена на нормально распределенную, что является естественным переходом, так как сеть применяет для оценок качества своей работы среднеквадратические отклонения (СКО). Отметим также существенное увеличение числа обучающих наборов: до 500 наборов в сравнении с 120 наборами, указанными в работе ( Пашенцев, 2023 ).

При модельных испытаниях ( Юдин и др., 2024 ) для получения обучающих наборов использовался стандартный маневр "циркуляция" (резолюция ИМО № 137¹). Данный маневр удобен для программной обработки, но дает ограниченную информацию о поведении модели, так как после перекладки руля на борт и входа в циркуляцию судно-модель достаточно быстро достигает установившегося состояния, и далее все кинематические параметры движения, кроме курса, практически не изменяются. Перспективным источником коррекции является стандартный маневр "зигзаг 20/20" (или 10/10); он разнообразен по характеру движений и изменению кинематических параметров, а также положению рулевого органа судна. Поэтому для обучения сети и получения результатов коррекции математической модели в качестве источника информации выбран маневр "зигзаг".

Материалы и методы

Для анализа выберем математическую модель в перемещениях ( Тумашик, 1978 ) для танкера типа "Архангельск" при состоянии в грузу. Расчет параметров модели произведем с помощью алгоритмов, представленных в работе ( Юдин и др., 2015а, с. 157). Модель плоского движения описывают три нелинейных дифференциальных уравнения относительно линейных скоростей судна vx , vy и угловой скорости го поворота вокруг вертикальной оси судна:

( m ⁺    ) dux' = ( m ^{+ Z} 22 ) ^U У “ ⁺ X^{k +} X^{a + X}w ^{+ P ,}

( m ⁺ ^ 22 ) ^ = ( m ⁺ \1 ) ^U x ® ^{+ Y}k ^{+ Y}a ^{+ Y}w ⁺ Yr ,

( Iz + ^ ) ^ = Mk + Ma + Mw + Mr .

В правые части дифференциальных уравнений (1) входят усилия и моменты различного характера: гидродинамического (индекс k ), аэродинамического (индекс а ), волнового (индекс w ), а также рулевые (индекс r ) и движительные (индекс е ). Для наших целей существенны гидродинамические силовые характеристики, так как именно в них входят постоянные, которые являются параметрами математической модели:

„   ( Cxz - Cx 0   Cxz - Cx 0   _D                           .„^ p A ₂

X_k = I--------- cos в + Cx 1 ■ sin ² в + Cx 2 ■ sin ³ в ' sin 2в I — L- v 2 ,

Y_k = ( 0,5 Cy в ■ sin2e ■ cose + Cy 2|sine|sinв + Cy 3 ■ sin ³ 2e|sin2e|)“ L ¹ v ²,

M_k = - ( Cm 1 ■ sin2в + Cm 2 ■ sin в + Cm 3 ■ sin ³ 2в - Cm 4 ■ sin ³ 2в|sin2в| - Ckm ® ■ v ² +

Ckm ω2             ρ A

+ Ckm rol ■ ro ro L +-------- ( v² + ro ² L ■ sinn)    L ¹ v .

π2

Силовые характеристики рассчитываются для модели в перемещениях ( Тумашик, 1978 ) с помощью группы формул (2).

Базовый набор коэффициентов модели определяет гидродинамические воздействия среды на корпус судна и усилия, возникающие на рулевом устройстве. Дальнейшие вариации параметров модели произведем с использованием этого набора. Он содержит 16 параметров модели, к которым добавлены 3 коэффициента масс корпуса и его момента инерции (19 параметров).

Параметры находятся с помощью большого числа формул и вычислительной техники по данным главных размерений судна и его теоретического чертежа. Расчеты проверены многократно ( Юдин и др., 2015б, с. 142) для различных типов судов: танкеров, рыболовных судов, сухогрузов, буксиров и т. д.

Результаты расчета параметров модели танкера типа "Астрахань" приведены в таблице.

Таблица. Базовый набор коэффициентов математической модели

Table. Basic set of coefficients of the mathematical model

Cx 0	0,05	Cy β	0,1322	Сm 2	2,53 E -03	Ckm ω1	–0,01215	k 11	0,05
Cxz	5,846 Е -02	Сy 2	0,6389	Сm 3	2,28 E -02	Ckm ω2	0,06604	k 22	0,7
Cx 1	–5,438 E -02	Сy 3	5,97E-02	Сm 4	–1,835 E -03	Cyra	2,60	k 66	0,8
Сx 2	1,347 E -03	Сm 1	4,81E-02	Ckm ω	7,59 E -02	Сxra	1,0	–	-

Для создания наборов, обучающих сеть, применен принцип вариативной генерации базовых параметров модели. Генерировалось нормальное распределение параметров вокруг средних значений, равных их базовым величинам, и с заданным средним квадратическим отклонением. Использовано преобразование Бокса – Мюллера, которое из случайных равномерно распределенных чисел Rnd(1) формирует числа, распределенные нормально. Эти преобразования имеют вид:

z l = yj - 2ln( v l) - cos(2n v 2), z 2 = J - 2ln( v l) - sin(2n v 2).

Здесь v1 и v2 распределены равномерно на отрезке [0, 1], z1 и z2 распределены нормально с нулевым средним и СКО, равным 1. Соответствующий программный код генерации приведен ниже в виде подпрограммы CreateVarModel на языке VB6 на примере вариаций параметра модели Cxz (см. таблицу). Число таких вариаций определяется в точке обращения к подпрограмме и определено глобальной переменной NumbVariants, которая увеличивается на единицу с каждым обращением:

Public Sub CreateVarModel()

' варьировать параметры случайно с нормальным распределением вокруг базы

' амлпитуда вариаций в процентах 10 %

If NumbVariants = 0 Then aa = 0 Else aa = 0.1 ' 10 %

With MyModelVar

GoSub zzz

End With

NumbVariants = NumbVariants + 1 zzz:

If rnd(1) > 0.5 then sw = 1 else sw = -1

Z = sw*Sqr(-2 * Log(Rnd(1))) * Cos(2 * i * Rnd(1))

Return

End Sub

После вариаций всех параметров внутри такой подпрограммы запускается программа ( Программный комплекс…, 2018 ) на испытание сгенерированной модели с помощью стандартного маневра "зигзаг 20/20". В процессе испытания фиксируется набор кинематических характеристик управляемости модели, который описан ниже. После завершения каждого испытания модели сгенерированные параметры и зафиксированные характеристики управляемости записываются в файл, затем процедура циклически повторяется установленное через NumbVariants число раз. Этот файл участвует в обучении сети для формирования регрессионной связи характеристик управляемости (входы) и параметров модели (выходы). Принципиально ничего не меняется в сравнении с циркуляцией, но обработка маневра "зигзаг" усложняется, что вызвано повышенными сложностью и информативностью самого маневра.

Опишем детально важную часть испытаний модели – процедуру обработки маневра "зигзаг". Согласно резолюции ИМО № 137 на судне, идущем прямолинейно фиксированным курсом К0 с постоянной скоростью, руль перекладывается, например, на правый борт на 20 ° . Курс судна растет, и когда он изменяется от начального К0 на 20 ° , руль перекладывается на 20 ° левого борта. Курс начинает убывать, и когда он станет меньше курса К0 на 20 ° , руль вновь перекладывается на правый борт на 20 ° . Цикл следует повторить три-четыре раза; ИМО рекомендует фиксировать время и величины максимального зарыскивания судна вправо и влево.

Скриншот рабочего окна программы, на котором показаны некоторые результаты исследования, приведен на рис. 1. В графическом координатном поле ( X, Y ) изображена траектория "зигзага 20/20". На нижнем (голубом) поле построены изменения во времени курса судна-модели и положения руля; отражены моменты перекладки положения руля; положение изменяется линейно с постоянной скоростью после перекладки. Точками отмечены моменты переключения положения руля и точки максимального зарыскивания. Задача исследования заключается в том, чтобы с помощью программы отыскать указанные точки и зафиксировать кинематические параметры движения в этот момент.

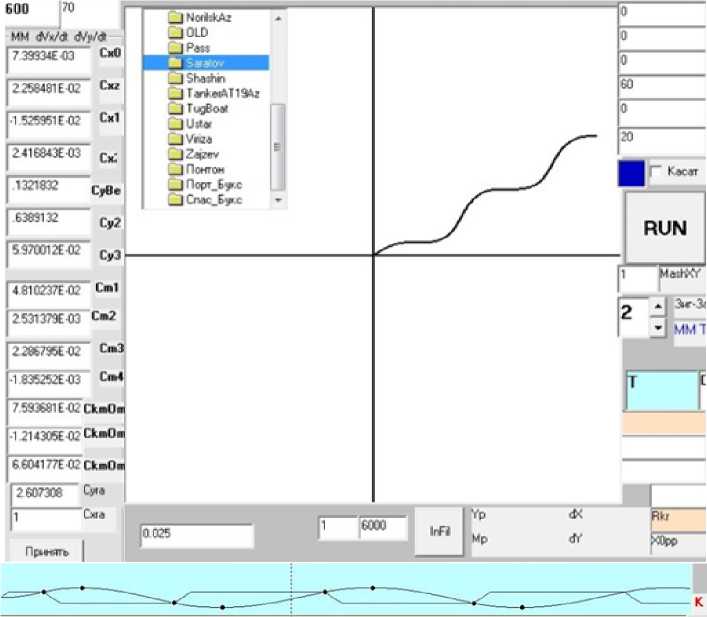
Рис. 1. Скриншот рабочего окна программы, выполняющей испытания математической модели движения судна Fig. 1. The main frame of the program that tests the mathematical model of the vessel's movement

В программу введены глобальные массивы для записи необходимых характеристик движения в требуемые моменты времени (времени события, координат судна, скорости, отклонения курса от начального значения, угловой скорости, положения руля):

Public Tzig(9), Xzig(9), Yzig(9) as Integer; Public Vzig(9), DKzig(9), Rulzig(9), Omzig(9) As Single.

Определим 3 первых зарыскивания, т. е. зафиксируем состояние модели при испытаниях в 6 точках.

Также введены необходимые для дальнейших испытаний глобальные переменные (среди них и логические сигналы):

delRuldK – разность между положением руля и отклонением курса от начального значения;

IsSeekEqulRK As Boolean – сигнал поиска равенства отклонения курса от начального и положения руля;

IsSeekMax As Boolean – сигнал поиска максимума отклонения курса от начального значения.

В каждом единичном цикле интегрирования модельных уравнений движения выполняется ряд операций по анализу состояния модели. Для упрощения алгоритма поиска следует учесть тот факт, что нет необходимости параллельно вести поиск максимума и равенства отклонения курса с положением руля. На рис. 1 показано, что точки с этими свойствами сменяют друг друга. Поэтому введены булевы переменные (семафоры), сигналящие программе, что следует искать в данный момент. Так, вначале открывается семафор для поиска только равенства положения руля и отклонения от начального курса. Когда это состояние достигнуто, данные сохраняются в списке элементов массивов с номером NP найденной точки:

Tzig(NP) = Т: Xzig(NP) = xk1: Yzig(NP) = yk1: Vzig(NP) = Vk, DKzig(NP) = dellk: Rulzig(NP) = rulk: Omzig(NP) = omk1 * cc, а номер точки увеличивается на единицу NP = NP + 1.

Соответствующий семафор выключается (IsSeekMax = false), а другой включается (IsSeekEqulRK = true). Процесс продолжается до исчерпания числа необходимых шести точек. Точки с четными номерами 0, 2, 4 будут относиться к равенству отклонения курса от начального и положения руля, а точки с номерами 1, 3, 5 – к максимуму зарыскивания. Таким образом, получаем 6∙7 = 42 маневренных характеристики для 6 точек.

С учетом всех изменений и описанных дополнений программа запускается обычным образом на испытание маневра "зигзаг 20/20" с повторением 600 раз при изменяющихся параметрах модели. В завершение такого цикла все результаты (параметры модели и маневренные характеристики) записываются в текстовый файл в виде строк – наборов данных для последующего обучения сети.

Построение нейронной сети и ее обучение

После получения массива исходных данных происходит конструирование сети и ее последующее обучение. Используем пакет Statistica Neural Networks, Release 4.0E, StatSoft Inc. (далее – пакет SNN2).

Запуская программу, получаем возможность выбрать для работы файл данных; выбираем созданный выше массив данных TestModZig600.txt и получаем на экране форму, показанную на рис. 2. В отличие от выбора базового подхода к построению сети ( Пашенцев, 2023 ), выберем вариант Advanced – использование интеллектуального решателя проблем IPS (заголовок всех последующих форм диалогов). При таком выборе следует более длинная интерфейсная процедура формирования задания на построение сети. Ее интуитивно понятные этапы опускаем, но обращаем внимание на наиболее важные из них.

Рис. 2. Выбор интеллектуального решателя проблем для формирования и обучения сети Fig. 2. Selecting an intelligent problem solver for network formation and training

В первую очередь это относится к заданию входных и выходных переменных, что выполняется с помощью форм, которые показаны на рис. 3 и 4. Сформированные нами 600 наборов данных содержат 19 параметров модели судна в качестве выходных переменных и 42 маневренные характеристики в качестве входных переменных.

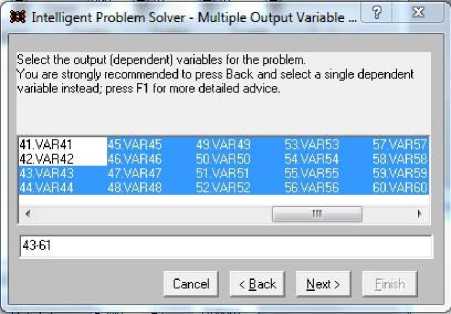
Рис. 3. Выбор выходных переменных из общего набора переменных Fig. 3. Selecting output variables from a common set of variables

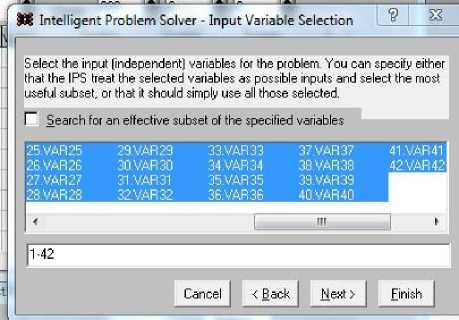
Рис. 4. Выбор входных переменных из общего набора переменных Fig. 4. Selecting input variables from a common set of variables

Форма на рис. 3 позволяет выбрать выходные переменные сети. При необходимости выделить несколько выходных переменных следует нажать кнопку Multipl… Нами выделены переменные 43–61 – параметры модели.

Форма на рис. 4 дает возможность выбора входных переменных. Здесь по умолчанию можно выбрать произвольное число переменных, но система предлагает выбор переменных, которые не фигурировали в выборе диалога рис. 3, т. е. переменных 1–42 – маневренных характеристик в испытаниях "зигзаг 20/20", описанных выше. На форме рис. 4 снимем чек, дающий право системе варьировать число входов при поиске эффективной сети. Таким образом задаем, чтобы на входе были сохранены все 42 компоненты.

Следующий этап определяется стандартным вариантом построения сети; выдержка из него приведена на рис. 5. Массив обучающих данных из 600 наборов разделен на три группы: 400 наборов для обучения (Training), 100 наборов для проверки качества обучения (Verification) и 100 наборов для тестирования (Test). При этом выбор Randomly дает возможность случайного перемешивания наборов в процессе работы системы. В противном случае наборы используются строго так, как они распределены в диалоге.

Рис. 5. Определение массивов наборов для тренировки, проверки и тестирования сети Fig. 5. Defining arrays of sets for training, verification and testing the network

В диалоге рис. 6 происходит выбор сетевой архитектуры из предложенных вариантов. Многослойный персептрон – наиболее распространенная форма сетевой архитектуры. Такие сети требуют итеративного обучения (подобный процесс обучения может быть довольно медленным), но они компактны, быстро работают после обучения, чаще приводят к лучшим результатам, чем сети иной архитектуры. В данном случае выбран трехслойный персептрон, имеющий один (средний) скрытый слой.

Рис. 6 Выбор структуры сети Fig. 6. Selecting a network structure

Форма рис. 7 завершает задание структуры сети. Данный диалог задает число нейронов в скрытом слое или разрешает программе его подбирать. Чтобы задать указанное число, следует снять отметку в поле Determine…, после чего выбрать число нейронов для трехслойного персептрона. В этом случае получаем одну сеть с установленными параметрами.

Рис. 7. Задание числа нейронов скрытого слоя для трехслойного персептрона Fig. 7 Setting the number of hidden layer neurons for a three-layer perceptron

Если же чек в поле Determine… сохранить, то можно использовать все возможности интеллектуального решателя проблем IPS. Система сама будет варьировать число нейронов скрытого слоя, обучать сеть, проверять результат и оценивать точность прогноза с помощью средней квадратической погрешности СКП (RSME). Сохранение этих результатов и способы их демонстрации представлены на рис. 8 – диалоге, который определяет число сохраняемых сетей и принцип их сохранения.

Форма рис. 8 определяет набор важных показателей, с которыми будет работать интеллектуальный решатель проблем IPS.

Рис. 8. Определение числа сохраняемых сетей и иерархический принцип их сохранения

Fig. 8. Determination of the number of saved networks and the hierarchical principle of their preservation

Вначале зададим число сетей, которые будет сохранять система; установим число 10, так как дополнительный анализ большего числа сохраненных сетей требует времени.

Затем укажем, какие сети сохранять: с лучшими результатами или с учетом баланса между качеством результатов и сложностью сети. При этом под качеством подразумевается средняя квадратическая погрешность (СКП) результатов, а под сложностью сети – число входов и число нейронов в скрытом слое.

Последний выбор этого диалога: увеличивать набор сохраненных сетей или заменять худшую сеть в наборе из 10 полученной позже, но лучшей сетью; выбираем варианты Balance и Replace.

Результаты процесса обучения сети

Основные этапы построения сети выполнены в показанных выше диалогах (рис. 2–8), остальные этапы не представляют сложности. Сделанные выше выборы в диалогах определяют стратегию обучения сети и ее использования. Когда нажата финальная кнопка последней интерфейсной формы, система выполняет предписанные действия, т. е. на базе введенных наборов данных формирует сеть, обучает ее, проводит прогноз на тестовых данных, определяет СКП прогноза и записывает сеть в сетевой набор (рис. 9). Первый выбор (DataSheet…) дает системе указание приводить результаты не только по всем входным наборам данных в совокупности, но и для каждого выбранного набора. Наиболее важно установить опции для получения сводных статистических данных (Summary Statistics) и результаты анализа чувствительности (Sensitivity Analysis). Последний выбор дает возможность определить, от каких входных переменных и в какой степени зависит конечный прогностический результат. Данный диалог является конечным в длинном ряду подготовки работы решателя IPS.

Рис. 9. Задание опций для представления конечных результатов Fig. 9. Setting options for presenting final results

Нажатие кнопки Finish запустит систему, часть полученных результатов немедленно появится на мониторе автоматически, часть других возможностей анализа реализуется обращением к верхней линейке задач в основном кадре SNN.

Затем те же действия выполняются с вариациями наборов исходных данных, структуры новой сети и определения СКП ее прогноза. Сеть снова записывается в сетевой набор, если не превышен лимит набора, равный 10. Когда этот лимит превышен, то СКП текущей сети сравнивается с самой большой СКП из уже заполненного набора сетей. Если новая СКП меньше (прогноз точнее), то записанная, худшая по точности сеть удаляется из набора, а новая включается в него. Здесь может работать дополнительное соображение сложности сети – выбирается более простая сеть, хотя и с худшим результатом прогноза, что было определено нами (Balance) в диалоге рис. 8. Этот выбор зависит от особенностей решаемой проблемы и специфических требований к результатам.

Среди информации, которая появляется на мониторе в качестве финального результата, в первую очередь интересен список сетей, записанных системой в сетевой набор (рис. 10). В столбцах списка для каждой из 10 сетей приведены следующие результаты: число нейронов скрытого слоя; СКП для тренировочного, проверочного и тестового наборов данных; качество работы по наборам. У десятой сети поставлена отметка * как у лучшей среди представленных сетей: она имеет самые малые СКП по трем категориям множеств и лучшее качество.

Под качеством здесь понимается отношение суммы квадратов ошибок прогнозов к сумме квадратов отклонений от среднего значения. В описаниях работы с сетями это значение называется производительностью – один из вариантов перевода английского термина Performance (три последних столбца в таблице рис. 10). Эти же величины появляются в исследованиях и под наименованием S.D. Ratio, что вполне соответствует указанному выше смыслу качества сети как отношения. Производительность сети не характеризуется одной величиной и является более сложным понятием, включающим точность прогноза, сложность архитектуры сети, время работы, а также ресурсы, потребляемые при работе сети.

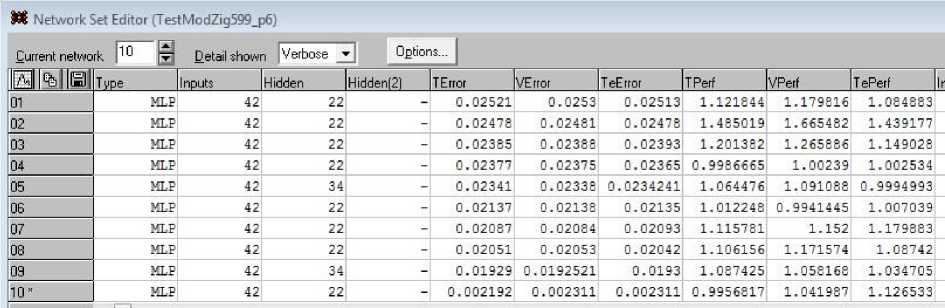
Рис. 10. Список 10 сетей, полученных в результате работы интеллектуального решателя проблем Fig. 10. List of 10 networks resulting from the intelligent problem solver

Одновременно со списком сетей, отобранных решателем, на экране возникает форма рис. 11, в которой указываются сводные данные. Эта форма включает большой объем данных; в матрице результатов содержится 61 столбец и 600 строк (она не помещается в один скриншот).

M Run Data Set                                                                       | □ | |~E~ || S3

Outputs shown (Variables 2] Run |   <-Data Set |

RMS Error Train 0.01852 Verify 0.01856 Test 0.01842

Ml^llisi	VAR43	VAR44	VAR45	VAR 46	VAR47	VAR48	VAR49
01	0.004162	0.0756577	-0.06696	-0.001906	0.1728618	1.240472	0.1675291 *
02	0.0044	0.07528	-0.06724	-0.001838	0.1737428	1.275811	0.163765L
03	0.004117	0.07575	-0.06697	-0.00192	0.1731986	1.23677	0.1681225
04	0.004392	0.07534	-0.06713	-0.001835	0.1744011	1.266257	0.1633506
05	0.004125	0.07569	-0.0668	-0.001909	0.1725818	1.227167	0.1677794
06	0.004142	0.07566	-0.06705	-0.001916	0.1724395	1.246099	0.168222
07	0.00407	0.07578	-0.06685	-0.001929	0.1728719	1.225949	0.1686529
08	0.003933	0.07603	-0.06674	-0.001971	0.1726551	1.208421	0.1708709
09	0.004002	0.07584	-0.06689	-0.001957	0.1711125	1.227351	0.17081
10	0.004157	0.07566	-0.06696	-0.001908 0.1726316		1.24036	0.1677447
11	0.0039	0.0752	-0.06639	-0.00195	0.1637077	1.203292	0.1727825
							►

Рис. 11. Результаты определения выходных параметров, найденных по всей совокупности входов

Fig. 11. Results of determining output parameters found across the entire set of inputs

Найденные сетью выходные параметры указаны в 19 столбцах (var43–var61), следующие за ними столбцы отражают их погрешности в режиме тренинга и погрешности в режиме проверки. Эти параметры и погрешности приведены для всех 600 наборов входных данных, т. е. матрица имеет размер (600 × 61). В рамках SNN ее можно изучать визуально, перемещаясь с помощью вертикального и горизонтального слайдеров. Но данную матрицу легко перенести в другую среду нажатием одной из показанных ниже кнопок слева вверху над матрицей (слева направо: файл SNN, ClipBoard, файл текстовой):

Далее можно размещать записанные таким образом результаты в Excel, MathCad и т. п.

Важно, что система SNN дает возможность получить результаты не только по всему набору исходных данных, но и по любому одиночному набору из них. Это делается простым переходом по Run\Run Single

Case, выбором в поле Case No нужного номера набора и нажатием кнопки пуска Run. Результат такой процедуры приведен на рис. 12, где для сети 10 выбран 24-й набор входных переменных.

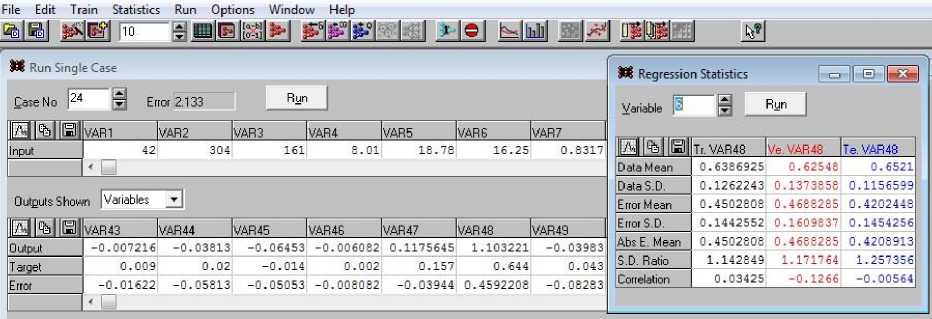
Рис. 12. Результаты прогноза для 19 выходных переменных и 24-го набора входных данных. Статистические данные для 6-й (var48) выходной переменной (справа) Fig. 12. Prediction results for 19 output variables for 24th input datasets.

Statistics for 6th (var48) output variables (right)

Вверху показана часть из ряда входных данных var1–var49, ниже – полученные выходные параметры модели var43–var49, их целевые значения и погрешности. Справа показана статистика по шестой выходной переменной (var48 в счете системы), где приведены подробные данные о точности результата прогнозирования именно этой переменной, номер 6 которой выбран в поле Variable формы Regression Statistics. Изменяя этот номер и нажимая кнопку Run, получаем поочередно статистики для всех 19 выходных результатов var43–var61.

Подобную процедуру можно выполнить с любым набором входных данных, например, с теми, которые ни в каком качестве (Train, Verify или Test) не участвовали при обучении сети. Выполним процедуру с помощью перехода по Run\Run One-Off Case, открывая форму рис. 13. В форме в строку Input можно ввести любые значения, нажать Run и в нижней строке Output получить набор выходных переменных от var43 до var61.

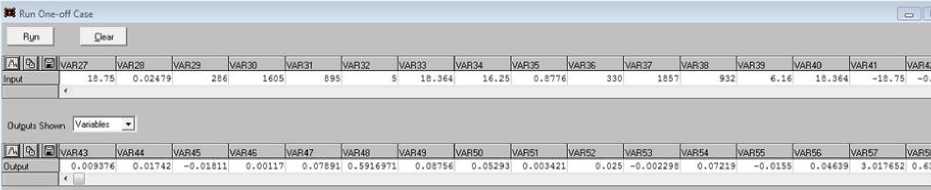
Рис. 13. Введение произвольных входных значений и получение для них параметров модели Fig. 13. Entering arbitrary input values and obtaining model parameters for them

Таким образом находятся параметры математической модели движения судна, при которых она будет наилучшим образом соответствовать введенным маневренным характеристикам. Модель легко изменить произвольно в вертикальном блоке параметров слева непосредственным вводом новых значений в выбранные текстовые поля. Произведем следующие замены четырех параметров: Cx 0 – 0,007 на 0,0063; Cy β – 0,13 на 0,143; Cm 1 – 0,048 на 0,0432; Cyra – 2,6 на 2,86. Нажав кнопку принятия новой модели "Принять", запустим маневр на выполнение и получим на координатном поле траекторию нового "зигзага" (синий цвет). Предварительно сделан запуск с параметрами базовой модели, ее трек для сравнения показан черным цветом. Данные файла траекторных измерений вдоль синего трека введем в строку Input формы рис. 13 как входные данные, не участвовавшие в обучении сети. Нажав кнопку Run, получим в строке Output параметры модели, соответствующие данным маневренного испытания.

Именно такая задача была поставлена нами как основная в начале работы; на данном этапе исследований появляется возможность ее решения, для этого имеются все необходимые средства. Сформируем данные для проверки такого подхода. На рис. 14 повторим форму рис. 1, где демонстрировалось получение набора из 600 данных для обучения сети. Программа повторяла процедуру интегрирования уравнений движения "зигзаг" с варьированными параметрами модели и фиксировала кинематические характеристики 600 траекторий. В базовой модели мы изменили вручную часть ее параметров и получили траекторию для новой модели. Сохраненные в файле характеристики ее трека введем в форму диалога рис. 13 и получим скорректированные параметры модели для этого трека, завершив процедуру решения проблемы.

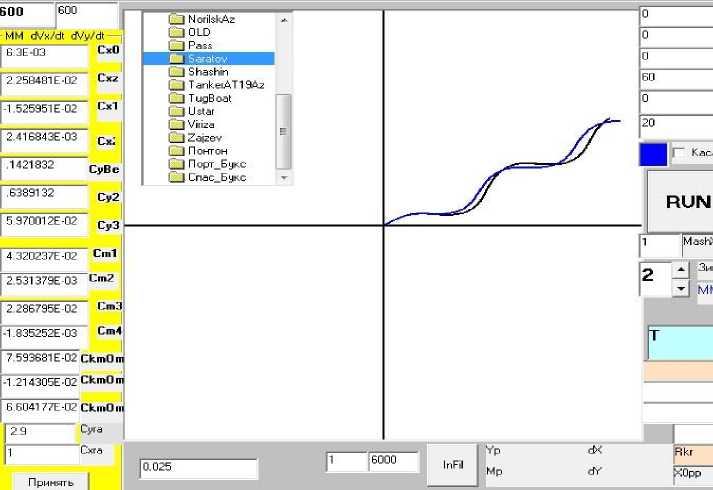
Рис. 14. Ручное изменение 4 параметров модели

Fig. 14. Manual change of 4 parameters of the model

Результаты и обсуждение

Окончательную проверку результата прогноза проведем с помощью той же программы, которая формировала обучающее множество. Прежде чем продемонстрировать результат визуально (на графике), рассмотрим альтернативу для нейронной сети, используя сгенерированный массив для обучения. Переведем его в пакет Mathcad15 и считываем в него матрицу размером 600 × 61. Выделив в ней две подматрицы трековых измерений и варьированных параметров модели, найдем траекторию, наиболее близкую к той, которая получена при ручном изменении параметров модели, с помощью коротких подпрограмм в стиле Mathcad. Сравнение производится не с реальными данными, а их нормированными образами, так как данные очень неоднородны по величине (например, присутствуют координаты, имеющие порядок тысяч, и угловые скорости поворота порядка тысячных долей). На самом деле пакет SNN предварительно делает с неоднородными данными то же самое (режим Pred\Post), но этот процесс от нас скрыт. Мы делаем его явным, позволяя производить корректно дальнейшие сравнения траекторий.

На рис. 15 показаны три программы, которые решают задачу сравнения траекторий. Вверху слева VNorm(V) нормализуют вектор, справа MNorm(M) нормализует матрицу. При нормализации значения всех переменных сводятся к отрезку [0, 1], что делает дальнейшие сравнения корректными. Программа внизу ищет минимум стандартного отклонения среди строк матрицы M от заданного вектора V. Результатом работы программы является номер найденной траектории.

VNonn(V) >

minV 4— min(V)

maxV 4— max(V)

MNoim(M) :=

col 4- cols(M) for nc € 0.. col — 1

VoUt 4—

V - minV ' maxV - minV /

VN 4- VNoiJm^.I

MN^^VN

return Vout

return MN

SRAWN_VcM(M,V) :=

S<- 99

col 4— cols(M) for nee 0.. col - 1

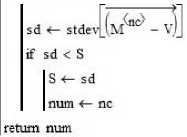
Рис. 15. Программы нормализации вектора и матрицы (вверху) и программа поиска строки матрицы с минимальным отклонением от заданного вектора

Fig. 15. Vector and matrix normalization programs (top) and program for finding a matrix row with minimal deviation from the given vector (bottom)

На рис. 16 представлено графическое координатное поле программы, которая формировала обучающее множество (рис. 1). На поле нанесены четыре траектории, которые получены разными способами: черная – траектория базовой модели; синяя – траектория модели, возникшей при изменении четырех параметров базовой модели; зеленая – траектория модели, которую дала система SNN; красная – траектория, выбранная по минимуму отклонения от синей траектории из обучающего множества.

Нормализуем матрицу траекторий из обучающего массива (обозначим LDTNbx) и вектор траектории с ручным изменением 4 параметров модели (обозначим NormIZMbx). Применив к ним программу сравнения num=SRAWN_VcM(LDTNbx, NormIZMbx), получим num = 102, т. е. "свойством лучшей близости" обладает 102-я траектория из массива 600 траекторий.

Найдем СКО 102-й траектории и траектории, которую определила нейросеть в режиме Run One-Off Case (рис. 13). Ее нормализованный вектор имеет обозначение NormKorrTrack, которое указывает на тот факт, что эта траектория – продукт корреляции модели. Используя stdev (встроенную функцию Mathcad) для вычисления обоих СКО, найдем stdev (NormIZMbx - LDTNbx^2)

= 4,028 - 10 - 3 , stdev I ( NormIZMbx - NormKorrTrack ) l = 6,389 - 10 ^{- 3}. (3)

Получен интересный результат – СКО траектории, выбранной из обучающего массива, в 1,5 раза меньше, чем СКО траектории, предложенной SNN, хотя оба СКО убедительно малы. Данный результат демонстрируют графики, указанные на рис. 16. Визуально показано, что красная траектория ближе к синей траектории по сравнению с зеленой линией в соответствии с результатом (3). На графическом координатном поле видна только геометрическая близость траекторий, а в ходе расчета среднеквадратических отклонений сравниваются также и кинематические характеристики.

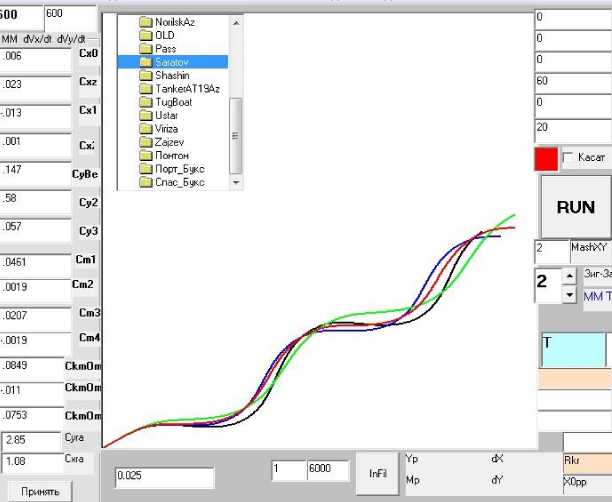
Рис. 16. Четыре траектории маневра моделей, полученные разными способами

Fig. 16. Four maneuver trajectories for models obtained in different ways

Анализ чувствительности

Нейронная сеть обладает возможностью анализа влияния входных переменных на выходные результаты. Выберем Statistics\Sensitivity из верхней линейки задач. Система открывает форму, часть которой, в силу протяженности, показана на рис. 17. Для каждой входной переменной даны три значения: Rank (ранг), Error (погрешность), Ratio (отношение).

Рис. 17. Показатели чувствительности переменных входа – степени их влияния на выходные результаты Fig. 17. Sensitivity indicators of input variables – the degree of their influence on output results

В строке Error приводится СКП, которая достигается, если данную переменную проигнорировать на входе. Чем она меньше и ближе к базовой СКП, тем переменная менее значима.

Ratio есть отношение полученной при этом СКП к ее первоначальному значению 0,002233 (см. в поле Baseline errors вверху формы слева). У менее значимой переменной Ratio будет также меньше. Система присваивает каждой переменной ранг тем больший, чем меньше Ratio. Если погрешность от игнорирования переменной возрастает, ее Ratio также растет, ей присваивается малый ранг; переменная более значима. Так, переменная var13, у которой СКП равна базовой и отношение равно единице, получает самый высокий ранг 42; она практически незначима для системы оценок. Переменная var10 имеет отношение 1,85842 (наибольшее значение) и получает ранг 1; она первая среди входов по значимости. Все остальные переменные получают ранги от 2 до 41, так как входных переменных всего 42.

Информация о значимости входных переменных способствует решению вопроса об упрощении проведения маневренных испытаний для получения входных значений. Это особенно важно для натурных испытаний, проводить которые достаточно сложно и любое их упрощение дает уменьшение потребных для этого ресурсов.

Заключение

Проведенные этапы коррекции параметров математической модели движения судна по результатам маневренных испытаний (модельных, натурных) позволяют сделать ряд выводов:

• 1.    Нейронная сеть способна решить проблему регрессии 42 входных переменных на 19 выходных. Варьируя в стандартном режиме архитектуру сети, которая была найдена решателем IPS как лучшая, можно дополнительно повысить точность результатов коррекции.

• 2.    Альтернативно полученному сетевому результату применяется прием простого перебора всех обучающих траекторий; траектория, ближайшая к заданной, находится в режиме ручной вариации ее параметров. Среднее квадратическое отклонение такой траектории в полтора раза меньше по сравнению с отклонением траектории, найденной сетью.

• 3.    Трудовые затраты на выполнение указанных способов примерно одинаковы; один из них требует освоения непростого сетевого пакета SNN, другой – умения программировать в Mathcad, работать с матрицами высокого порядка для их разделения, нормализации и подсчета отклонений; нейронная сеть выполняет данные процедуры самостоятельно (без участия оператора).

Преимущество обученной нейронной сети заключается в возможности анализировать степень влияния каждой из входных переменных на выходные, что открывает путь к обоснованному упрощению математических моделей, удаляя из них параметры, которые не влияют на конечный результат. Эта интересная и важная проблема оставлена для последующих исследований.