Маневренные характеристики судна как функции параметров его математической модели

Для точной идентификации параметров математической модели судна приходится затрачивать значительные материальные и временные ресурсы. Это включает постановку самих натурных испытаний, начиная с разработки методики их проведения, собственно натурные испытания, зачастую в сложных гидрометеорологических условиях, и последующую обработку результатов испытаний. Такая обработка может показать необходимость новых испытаний с повторением описанного технологического цикла. Затрачивая большие усилия для точной идентификации параметров математической модели судна, следует каждый раз оценивать, в какой мере погрешности в определении этих параметров скажутся на погрешностях оцениваемых с их помощью маневренных характеристик судна или траекторий самих маневров.

Такая задача для общей математической модели является весьма актуальной и, скорее всего, может быть решена только численными методами. Это утверждение особенно верно для того случая, когда параметры модели идентифицируются аналитически минимизацией функционала, соответствующего дифференциальным уравнениям, а не минимизацией суммарных отклонений модельной траектории от траектории фактической. В этом случае реальным является простое "проигрывание" модели при вариации ее параметров с изображением траекторий маневров и последующим подсчетом отклонений траекторий от некоторой базовой траектории. Однако, учитывая большое число параметров, входящих в модель, такой путь представляется не слишком перспективным, поскольку не выделяется влияние каждого из параметров модели.

Чтобы подтвердить это соображение, приведем результаты вариации параметров полной модели судна. Для анализа выбраны два дифференциальных уравнения управляемости судна, которые мы запишем в следующем виде:

d β / dt = – ( С y^β ⋅ β + С y^ββ ⋅ β | β |) ( v / L ) + С y^ω ⋅ ω + С y^δ ⋅ δ ( v / L ), d ω / dt = – ( С m^ω + С m^ωββ ⋅ β ² ) ω ( v / L ) + ( С m^β ⋅ β + С m^δ ⋅ δ )( v / L ) ² ,

где v – скорость судна, β – угол дрейфа, ω – угловая скорость, L – длина судна, δ – угол кладки руля, а C с различными индексами представляют собой соответствующие численные коэффициенты модели.

Структура этих уравнений, способ определения и обозначения параметров С c верхней и нижней индексацией соответствуют справочнику Гофмана А.Д. (1988) и несколько отличаются от ( Справочник , 1985). При использовании модели были изменены знаки отдельных параметров так, чтобы все они были положительны, соответственно изменились и знаки членов дифференциальных уравнений (1). Согласно такой модели, для танкера "Саратов" в балласте были вычислены следующие значения параметров С :

С y^β = 0.4;        С y^ω = 0.46;       С y^δ = 0.39;       С y^ββ = 0.94;

С m^β = 2.4;        С m^ω = 3.0;       С m^δ = 4.5;        С m^ωββ = 6.2.

Далее были рассчитаны модельные траектории для трех совокупностей параметров: первая – исходная совокупность (2), вторая и третья – с измененными примерно на 10 % параметрами в сторону увеличения и уменьшения. Полученные при этом траектории для v = 2 м/с, L = 147 м и кладке руля 15° п/б представлены на рис. 1. Сравнивать такие траектории в целом не просто. Чтобы дать какую-то численную

оценку их близости, сравнивались значения координат на траекториях с дискретностью в 1 сек. для 1000 точек в одинаковые моменты времени. Крайние две из этих трех траекторий дали средние квадратические отклонения по координатам Х и Y : □ X = 112 м, c Y = 124 м. Это значительные отклонения, но они вызваны тем, что сравнение координат проводилось в одинаковые моменты времени, т.е. в отклонения вошли неодинаковые темпы движения по траекториям. Понятно, что сравнение такого рода не очень удобно для практического использования. Поэтому ниже мы будем применять способ сравнения моделей с измененными параметрами по отдельным маневренным элементам.

• 2.    Установившаяся циркуляция

Для реализации этой идеи выберем ту же модель (1) при начальной скорости v = 2 м/с, начальном курсе 0 град., и перекладкой руля линейно за 7 сек. из ДП до значения 20 град. Вначале найдем базовые значения характеристик установившейся циркуляции, т.е. их значения при исходных параметрах модели. Положив производные угла дрейфа и угловой скорости нулевыми, найдем условия стационарного состояния объекта. Это два алгебраических уравнения относительно стационарных значений угла дрейфа в с и угловой скорости поворота го с :

Рис. 1. Сравнительные траектории при ± 10 % вариации параметров модели судна (кладка руля 15 ° , начальный курс 30 град., кривая 1 - базовая, 2 и 3 - +10 % и -10 %, соответственно)

- ( С у^в в с + С у^№ -в с в l)( v / L ) + С у^т - Го с + С у⁸ -8 ( v / L ) = 0, - ( С т^Ю + С т^Ювв- в с ^? ГО> ( V / L ) + ( С т^в -в с + C m⁸ 8 )(V / L ) 2 = 0.

Из второго уравнения системы (3) получим выражение для установившейся угловой скорости поворота:

го = [( С т^в -в с + C m⁸ 8 ) / ( C m ™ + C m ^ ⁸ в с ²)] ( V / L ).

Подставив его в первое уравнение, найдем нелинейное алгебраическое уравнение для значения установившегося угла дрейфа в с :

С у^вв - С ^го - в с ³ | в с | + С у^в - ^ -в= ³ + ( С у⁸ - С то* ■ в с ² - 8 + С у^вв - C m ™ -в- - | в с |) + + в с ( С у^в - C m ™ - С у ™ - C m ' ) + 8 " С у⁸ - C m ™ - С у ™ - C m⁸ ) = 0.

У этого алгебраического уравнения было записано три варианта: одно - исходное (5) четвертого порядка, другое - третьего порядка, в котором опущен член четвертого порядка, и, наконец, уравнение второго порядка, в котором опущены члены четвертого и третьего порядка по углу дрейфа. Заметим, что традиционно решается именно это третье уравнение как обычное квадратное уравнение. Это естественно, если решение производится аналитически, так как общего решения уравнений третьего и четвертого порядка мы записать не сможем. Но в нашем случае использованы вычислительные средства, поэтому в целях сравнения были решены все три вида уравнений для трех различных кладок руля. Результаты таких расчетов приведены в табл. 1 для судна в балласте, скорость хода 6.9 м/с.

Таблица 1. Сравнительные результаты расчета характеристик установившейся циркуляции

Уравнение	4 степени	3 степени	2 степени
	Кладка руля 5 °
в с , °	15.2	16.0	17.9
го с , ° /мин	14.0	15.3	18.5
R c , м	491	450	372
	Кладка руля 10 °
в с , °	20.7	22.6	26.7
го с , ° /мин	20.3	24.1	32.8
R c , м	339	285	210
	Кладка руля 20 °
в с , °	27.9	32.4	42.0
го с , ° /мин	28.6	39.6	67.2
R c , м	240	174	102

Эти результаты показывают, что упрощенное решение уравнения второго порядка дает искаженные результаты, опасные с точки зрения маневрирования. В частности, оно дает заниженные значения радиуса установившейся циркуляции и, следовательно, реальный маневр, основанный на этих значениях, может не вписаться в акваторию маневрирования. Именно поэтому для точности последующих выводов мы находим значения указанных характеристик только с помощью полного уравнения (5).

Найдем эти характеристики для кладки руля 20 град. при исходных значениях параметров модели (2) в с = 0.487 рад, т с = 0.008337 рад/c, R c = 239.9 м. Далее проведем вариации параметров модели судна С . Для этого изменяем каждый из параметров модели отдельно и определяем численно приращения в угле дрейфа, угловой скорости поворота и радиусе установившейся циркуляции (к их базовым значениям). Затем приближенно находим частные производные от этих характеристик по параметрам модели как отношение соответствующих приращений. Например, S R c/с С_у ^вв ® A R c / A С_у ^вв -частная производная от радиуса установившейся циркуляции по параметру С_у ^вв . Эту величину мы назовем коэффициентом влияния параметра С_у ^вв на радиус установившейся циркуляции. Все эти расчеты сведены в табл. 2, где под С i ⁰ подразумеваются базовые значения коэффициентов модели в порядке, перечисленном при их первом введении в (2), а под С i – их варьируемые значения.

Таблица 2. Результаты расчета коэффициента влияния на радиус установившейся циркуляции

	(	C y ™	С у8	Cy№	С тв	C m ™	C m8	C ™вв
С i 0	0.40	0.46	0.39	0.94	2.4	3.0	4.5	6.2
С i	0.44	0.50	0.43	1.02	2.64	3.3	4.9	6.5
R c, м	238	242	241	239	231	255	229	243
S Rl 5Ck м	-36.6	49.2	28.0	-17.2	-37.4	49.6	-26.2	11.5

Результаты табл. 2 позволяют легко определить, какие коэффициенты в большей степени влияют на определенную характеристику установившейся циркуляции и в какую сторону – увеличения или уменьшения. Так, на радиус установившейся циркуляции наиболее сильно влияют параметры C y ™ и C m ™ в сторону увеличения радиуса при увеличении этих параметров. Это позволяет, например, выбрать из возможного диапазона значений параметров С те из них, которые увеличивают расчетный радиус циркуляции. Такой расчет важной маневренной характеристики пойдет в запас безопасности плавания, так как позволит реально вписаться при повороте в ограниченную акваторию маневра. С другой стороны, параметр модели С_у ^в влияет на радиус установившейся циркуляции в другую сторону. Поэтому при интервальной оценке параметров модели значения параметры C y ™ и C m ™ надо выбрать на правой границе их интервалов, параметр С_у ^в - на левой границе. Именно такой выбор даст наибольшую безопасность рассматриваемого маневра.

Имея результаты табл. 2, можно рассчитать полную вариацию в определении каждой маневренной характеристики по формулам:

Ав с = SA C i ■ K i ; Ao = SA C i- K ™^ A R с = SA C i ■ K^R i , (6) где K * i - коэффициенты влияния соответствующей характеристики, A C i - вариации в определении (задании) параметров модели. При этом параметры С пронумерованы в порядке их первого появления, чтобы избежать здесь сложной индексации.

• 3.    Эволюционный период циркуляции

Проведем те же оценки для характеристик эволюционного периода циркуляции: обратного С 0 и прямого С п смещений, выдвига В и тактического диаметра Д т . Базовые значения этих характеристик при работе с моделью оказались равными, соответственно -0.427, 151, 377 и 275, все данные в метрах.

Коэффициенты влияния этих характеристик рассчитываются точно так же, как в табл. 2, и результаты их расчета приводятся в табл. 3.

Таблица 3. Результаты расчета коэффициентов влияния на характеристики эволюционного периода циркуляции: С ₀, В

С 0	-0.426	-0.590	-0.434	-0.506	-0.433	-0.362	-0.435	-0.459
В	375	378	376	380	369	252	371	390
SB I S C	-50	25	-12.5	75	-33.3	-62.5	-20	43.3

При работе с моделью фиксировались и моменты достижения максимального обратного смещения, изменения курса на 90 ° и 180 ° . Они также изменчивы при вариации параметров модели, но в меньшей степени, и потому не представлены в этих результатах.

Табл. 2 и 3 дают коэффициенты влияния, которыми удобно пользоваться, если необходимо найти абсолютные значения полных приращений маневренных характеристик, зная приращения параметров модели. Такая задача решается с помощью формул вида (6).

Если же перед нами стоит задача анализа, т.е. выявления параметров модели, оказывающих наибольшие влияния на те или иные характеристики, то удобнее представить соотношения (6) в процентной форме, которая выражает процентное приращение характеристики через процентные приращения параметров модели, при этом все соотношения становятся безразмерными. Для этого модифицируются значения коэффициентов влияния – делятся на базовое значение характеристики и умножаются на базовое значение параметра. Пересчитанные таким образом все коэффициенты влияния представлены в табл. 4. Там же приведены еще раз базовые значения параметров.

Таблица 4. Коэффициенты влияния параметров на характеристики циркуляции в процентном представлении

С i	С yβ	С yω	С yδ	С yββ	С mβ	С mω	С mδ	С ωββ
баз. знач.	0.4	0.46	0.39	0.94	2.4	3.0	4.5	6.2
KR i	-0.061	0.094	0.046	0.068	-0.389	0.584	-0.513	0.292
KВ i	-0.053	0.092	0.026	-0.031	-0.212	0.345	-0.746	-0.329

Данные, приведенные в этой таблице, позволяют решать все задачи анализа о влиянии параметров модели на маневренные характеристики. Например, следуя по строке K^R i , мы можем сказать, что угловая скорость поворота более всего влияет на радиус установившейся циркуляции через коэффициент С_m ^ω . Этот же параметр достаточно сильно влияет и на прямое смещение.

Следуя по строке, например, прямого смещения, можем утверждать, что на него сильнее всего действует параметр С_m ^δ , затем параметр С_m ^ωββ , причем их увеличение ведет к уменьшению прямого смещения. Все формулы типа (6) будут теперь выглядеть однотипно, например, для угла дрейфа:

∆ β с = ∑ K ^βij ∆ a ij .

• 4.    Начальная поворотливость судна

Воспользуемся уравнениями (1) и построим диаграмму поворотливости нашего судна. Для этого возьмем еще раз стационарный вариант этих уравнений (3), когда производные угла дрейфа d β / dt и угловой скорости поворота d ω / dt равны нулю. Отнесемся к этим уравнениям как к линейной системе двух уравнений относительно угла кладки руля δ и безразмерной угловой скорости ω ^∼ _с :

С y^ω ⋅ ω ^∼ с + С y^δ ⋅ δ = ( С y^β + С y^ββ ⋅ | β с |) β с , ( С m^ω + С m^ωββ ⋅ β с ² ) ω ^∼ с – С m^δ ⋅ δ = С m^β ⋅ β с

где ω ^∼ _с = ω _сL / v .

Фактически, это и есть уравнение диаграммы поворотливости, записанное в параметрической форме, в которой параметром служит угол дрейфа β _с .

Из системы (8) легко найти угловую скорость ω и угол кладки руля δ через угол дрейфа β _с , используя обычный метод Крамера (определителей). Запишем параметрические выражения для безразмерной угловой скорости и кладки руля через угол дрейфа:

ω ^∼ с = D ω / D = [ С y^δ ⋅ С m^β + С m^δ ⋅ ( С y^β + С y^ββ ⋅ | β с |) β с ]/ [ С y^ω ⋅ С m^δ + С y^δ ⋅ ( С m^ω + С m^ωββ ⋅ β с ² )],                ₍₉₎

δ = D δ / D = [– С y^ω ⋅ С m^β + ( С y^β + С y^ββ | β с |) ⋅ ( С m^ω + С m^ωββ ⋅ β с ² )] β с / [ С y^ω ⋅ С m^δ + С y^δ ⋅ ( С m^ω + С m^ωββ ⋅ β с ² )].

Очень просто изобразить графически, например, в пакете MathCad, эту параметрическую зависимость безразмерной угловой скорости поворота от кладки руля, которая и носит название диаграммы поворотливости. Далее мы приведем две таких диаграммы. Важной маневренной характеристикой, которая связана с диаграммой поворотливости, является начальная поворотливость судна. Ею называется производная от угловой скорости поворота судна по кладке руля в нулевой точке диаграммы, когда ω ^∼ = 0 и δ = 0. Эта производная характеризует устойчивость судна на прямом курсе. Найдем ее через параметры уравнений С_i :

dω∼/dδ = (dω∼/dβ)/(dδ/dβ) = [d(Dω/D) /dβ]/[d(Dδ/D) /dβ] = (D′ωD – DωD′) / (D′δD – DδD′), где все производные, обозначенные штрихом, понимаются как производные, взятые по углу дрейфа β.

Для вычисления начальной поворотливости надо положить в этом выражении угол дрейфа β = 0. Получим окончательно:

П 0 = ( d ω ^∼ / d δ ) 0 = ( С y^β ⋅ С m^δ + С y^δ ⋅ С m^β ) / ( С y^β ⋅ С m^ω – С m^β ⋅ С y^ω ).                 (10)

По знаку начальной поворотливости просто определяется устойчивость ( П ₀ > 0) или неустойчивость ( П ₀< 0) судна на прямом курсе. Прост и геометрический смысл начальной поворотливости – это тангенс угла наклона касательной к диаграмме поворотливости в начале координат. Чтобы не оперировать в дальнейшем бесконечно большими значениями, будем определять угол наклона этой касательной а , равный arctg( П 0 ). Тогда касательная с углом наклона а = 90 ° будет отделять диаграммы устойчивых судов от диаграмм неустойчивых.

Используем формулу (10) для расчета коэффициентов влияния параметров математической модели на начальную поворотливость. Сразу можно сказать, что коэффициенты влияния параметров С_у ^в и С_т " ^в равны нулю, т.к. они вообще не входят в выражение для П ₀. Это вполне естественно, потому что это параметры при нелинейных членах в , и, следовательно, не сказываются на производных, вычисленных в точке в = 0.

Как и выше, дадим результаты расчетов в виде табл. 5. Базовое значение начальной поворотливости в виде угла равно 21.2 ° . Для определения коэффициента влияния варьируем каждый параметр уравнения отдельно вокруг базовых значений и вычисляем приближенно коэффициент влияния (производную) как отношение приращений. Последняя строка табл. 5 дает коэффициенты влияния в процентном исчислении.

Таблица 5. Коэффициенты влияния параметров на начальную поворотливость

	С	С у "	С у8	С ув	С т	С т "	С т8	С "в
баз. знач.	0.4	0.46	0.39	0.94	2.4	3.0	4.5	6.2
знач.	0.44	0.48	0.43	1.02	2.45	3.3	4.9	6.5
П 0	10.4	37.8	21.9	21.2	27.2	9.8	22.3	21.2
сПa/ c h i,	-270	830	17.5	0	120	-38	2.75	0
%	-5.1	18.0	0.3	0	13.6	-5.4	0.6	0

Хорошо видно, что при всех вариациях параметров модели, судно остается устойчивым на прямом курсе, т.к. начальная поворотливость остается положительной. Там, где П ₀ увеличилось в сравнении с базовым значением 21.2 ° , начальная поворотливость стала больше, судно становится менее устойчивым. Это, в основном, действие параметров модели С_у " и С_т ^в .

Изменим все параметры на 10 % в такую сторону, чтобы максимально ухудшить начальную поворотливость. Возьмем следующие значения параметров модели:

С/ = 0.36; С у " = 0.5; С у⁸ = 0.43; С у^№ = 0.94;

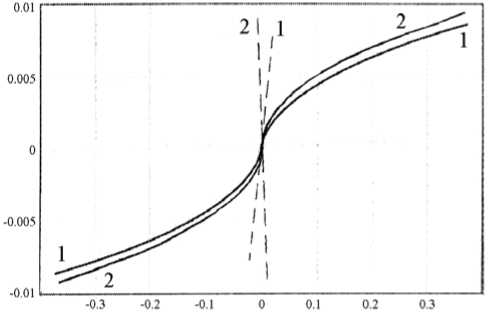
Рис. 2. Диаграмма управляемости для модели судна 1 – базовая модель, устойчивость, 2 – измененная модель, неустойчивость

С / = 2.65; С т " = 2.7; С т⁸ = 4.9; С т " ^№ = 6.9.

Такие вариации параметров приводят к значению начальной поворотливости П 0= -47.2 ° . Это значит, что судно, соответствующее этой модели, неустойчиво на прямом курсе. Кривые диаграмм поворотливости для этого и базового вариантов приведены на рис. 2. На нем, кроме самих диаграмм в осях "угол кладки руля – угловая скорость поворота", показаны и касательные к кривым в начальной точке.

Но это лишь предельный модельный результат, т.к. такое "согласованное" изменение всех параметров модели реально произойти не может. Параметры модели связаны между собой и находятся через одни и те же базовые размерные характеристики корпуса судна.

• 5.    Способность судна к одерживанию поворота

Под термином "одерживание" понимается остановка вращения судна, которое совершает поворот, перекладкой руля на борт, противоположный повороту. Одерживание – один из важнейших маневров, связанных с обеспечением безопасности судовождения. К сожалению, параметры этого маневра трудно нормировать, т.к. начальные и конечные его параметры слишком многообразны.

Поэтому решено сузить это понятие и считать одерживанием маневр вывода судна из установившейся циркуляции перекладкой руля на противоположный повороту борт, считая окончанием маневра момент равенства нулю угловой скорости поворота.

Предложено ( Гофман , 1988) оперировать двумя численными характеристиками, позволяющими оценить способность судна к одерживанию: t ₁ – время одерживания, т.е. время от начала перекладки нуля до конца одерживания, и 9 1 - угол зарыскивания, т.е. угол, на который успевает повернуться судно за время одерживания.

В дополнение к этим двум характеристикам мы введем еще одну, которая оказывается более полезной для судоводителя-практика. Это d 1 – максимальное поперечное смещение судна от линии пути в момент начала. Именно это расстояние определяет смысл всего маневра при уходе от опасности со стороны начального поворота. Названные характеристики вместе с траекторией маневра одерживания показаны на рис. 3.

Для анализа действия параметров модели на эти характеристики одерживания поступим в соответствии с нашей методикой, примененной выше. Будем давать отдельным параметрам модели примерно 10 % приращения и фиксировать изменения исследуемых характеристик. На основании изменения самих характеристик найдем коэффициенты влияния на них параметров модели. Как и ранее, сделаем это в абсолютном и процентном исчислении. Результаты таких испытаний модели и последующих расчетов приведем в табл. 6. Базовые значения характеристик до изменения параметров модели равны, соответственно: t 1 = 36 c, 9 1 = 17 ° , d 1 = 117 м.

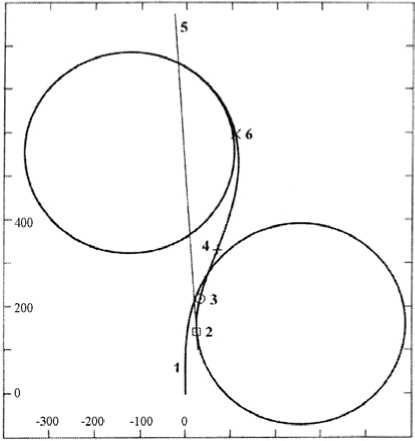
Рис. 3. Траектория судна при одерживании (1 – траектория, 2 – начало одерживания, 3 – конец перекладки руля, 4 – конец одерживания, 5 – путевая линия в момент начала маневра, 6 – положение судна в момент максимального смещения от линии 5)

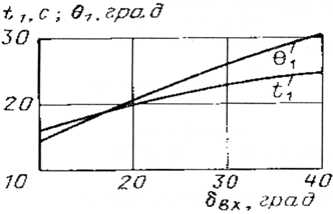
Рис. 4. Зависимости времени одерживания t ₁ и угла зарыскивания 9 1 от кладки руля 5 _вх, с которой совершалась начальная циркуляция судна ( Гофман , 1988)

Таблица 6. Результаты расчета коэффициентов влияния на характеристики одерживания

	С т в	C m ™	C m 5	C ™№
	2.64	3.3	4.6	6.7
t 1 , с	39	34	36	35
д 1 / 3^	12.5	-6.7	0	-2.0
%	0.8	-0.6	0	-0.3
9 1 , град	31.6	-6.4	21.3	8.8
59 1 / o a ij	131.7	-21.3	213	17.6
%	0.9	-0.2	2.8	0.3
d 1, м	122	124	103	125
d d i / d a ij	20.8	23.3	-140	16
%	0.4	0.6	-5.4	0.8

Отметим, что в табл. 6 присутствуют только параметры второго дифференциального уравнения поворотливости. Это означает, что параметры С_у ^в - С_у ^вв не влияют на изучаемые характеристики одерживания.

Пользоваться результатами этой таблицы, как и предыдущих аналогичных таблиц, очень просто – достаточно умножить каждый коэффициент влияния на изменение соответствующего параметра модели и сложить. Например, при 10 % изменении всех параметров второго уравнения получим изменение отклонения d 1 равным (0.4 + 0.6 - 5.4 + 0.8) ■ 10 % = 36 %. Это означает, что при данной комбинации изменения параметров d 1 станет равным 117 ■ 1.36 = 159 м.

Среди всех маневров одерживания при различных кладках руля на противоположный борт выделяют аварийное одерживание, когда руль перекладывается на максимальный угол. В этом случае все характеристики одерживания становятся функциями только параметров циркуляции, в которой находилось судно к моменту начала одерживания. Для этого случая в ( Гофман , 1988) приводятся зависимости t 1 и 9 1 от угла кладки руля, при которой происходила начальная циркуляция (рис. 4). Ниже мы добавим к этим характеристикам, показанным на рис. 3, еще и d 1 .

На рис. 5 приведена модельная траектория, характерная для аварийного одерживания. Выход из правой циркуляции с кладкой руля в 20° произведен кладкой руля в 35° на левый борт. При этом три важнейших характеристики маневра изменились и стали равными: ;1 = 26 c, 91 = 13.7°, d 1 = 62 м. Обращаем внимание на значительное сокращение поперечного смещения судна от начальной линии пути. Именно в этом и состоит смысл маневра, и это подтверждает полезность введенной нами характеристики. Две других характеристики также улучшились, но по их величине судоводителю не всегда просто быстро осознать эффект маневра. На рис. 5 результат их уменьшения виден как приближение точек 3 и 4 к начальной точке 2 маневра.

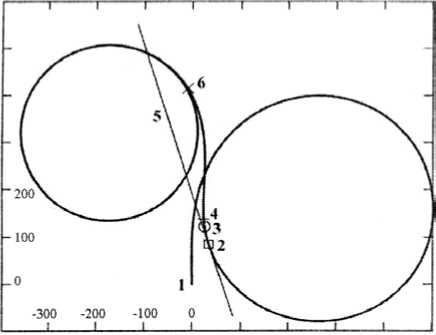
Рис. 5. Траектория судна при маневре аварийного одерживания (правая циркуляция при кладке руля

Построим, подобно ( Гофман , 1988), кривую бокового отклонения d 1 от начальной линии пути при аварийном одерживании в зависимости от кладки руля, с которой вошло судно в исходную циркуляцию. Для этого были сделаны испытания с математической моделью судна на ряде кладок руля, с которыми судно совершало установившуюся циркуляцию до начало маневра.

Эти результаты можно собрать в табл. 7, где приведены значения кладок руля и поперечные максимальные смещения. Простой просмотр результатов, полученных при испытании модели, 2оо, левая — при кладке 35°. Обозначения см. рис. 4) позволяет заключить, что их связь практически линейна. Чтобы увидеть это, представим график зависимости табл. 7 (рис. 6).

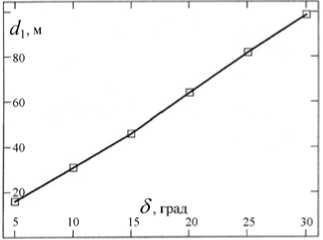
Рис. 6. Зависимость максимального поперечного смещения при одерживании от кладки руля до начала маневра

Из тех же модельных маневров можно получить еще одно полезное соотношение между временем окончания перекладки руля на другой борт t kr и временем конца одерживания t 1 . Эти результаты представлены в табл. 8 и на рис. 7.

Простой анализ говорит о близости к линейной зависимости, и ее можно аппроксимировать линейной функцией:

t 1 = (3 t kr – 5)/2.                      (11)

Формула (11) дает самое большое отклонение в крайней левой точке, приводя к значению t 1 = 18.5 вместо 16 c, однако такой результат идет "в запас" и потому ее можно применять как быструю оценочную формулу.

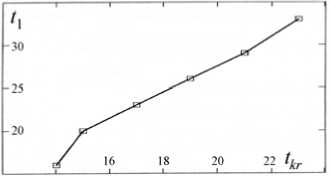
Рис. 7. Зависимость времени окончания аварийного одерживания от времени перекладки руля на другой борт

Таблица 7. Зависимость максимального поперечного смещения при одерживании от кладки руля до начала маневра

5	5	10	15	20	25	30
d 1, м	16	31	43	64	82	99

Таблица 8. Зависимость времени окончания аварийного одерживания от времени перекладки руля на другой борт

tkr , c	14	15	17	19	21	23
t 1 ,c	16	20	23	26	29	31

6. Заключение

Введенное в статье понятие коэффициентов влияния параметров математической модели судна на его маневренные характеристики, проиллюстрировано расчетами всех маневренных характеристик для танкера типа "Астрахань". Расчеты выполнены с помощью специально разработанной авторами компьютерной программы. Она позволяет максимально упростить сложные вычислительные процедуры и реализовать большое количество модельных маневров при вариации параметров модели. Эффективность использования коэффициентов влияния для "подгонки" модели судна показана в другой статье, публикуемой в настоящем номере.