Манипуляционные коды для систем с итеративной обработкой принимаемого сигнала

В настоящее время методы итеративной обработки находят все более широкое применение при построении устройств обработки сигналов в каналах с межсимвольной интерференцией, в частности, в КВ модемах. Основное достоинство итеративных методов – существенное уменьшение сложности процедур обработки при характеристиках качества близких к оптимальным. Одним из наиболее предпочтительных вариантов достижения высоких характеристик помехоустойчивости в каналах со сложными условиями распространения сигнала, характеризующимися как возможностью глубоких замираний, так и высоким уровнем помех, (в том числе в КВ каналах) является кодированная модуляция с битовым пе-ремежением (BICM) в сочетании с итеративной обработкой сигнала на приеме.

Известно, что на характеристики bIcM существенное влияние оказывает выбор метода манипуляционного кодирования. При неитеративных методах приема лучшим выбором всегда будет код Грея, а в случае итеративной обработки, как правило, требуются другие методы манипуляционного кодирования, выбор которых будет зависеть от характеристик канала связи и требуемых параметров достоверности.

Оптимизация вида манипуляционного кодирования является очень привлекательной задачей, поскольку достижение положительного эффекта, требуя определенных затрат на этапе проектирования, не затрагивает ни алгоритмов формирования передаваемого сигнала, ни методов приема, а фактически состоит только в выборе подходящего порядка нумерации сигнальных точек.

Известные манипуляционные коды

Наибольшее распространение получили манипуляционные коды Грея и Унгербоека (Set Partitioning, SP). Код Грея – это код, обладающий свойством, состоящем в том, что метки сигнальных точек, находящиеся друг от друга на минимальном евклидовом расстоянии, отличаются значением только одного бита. Никаких требований на метки сигнальных точек, находящихся на евклидовом расстоянии, большем минимального, кодом Грея не накладывается.

Таким образом, для многоточечных сигнальных созвездий кодирование Грея не уникально. Могут существовать разные коды Грея, обладающие разными характеристиками помехоустойчивости. Часто под кодом Грея подразумевают код, образованный при помощи регулярного алгоритма, предложенного самим Греем в [1].Иногда такой метод называют «отражением», а сами коды reflected Gray code. Данная разновидность кодов Грея обладает наилучшими характеристиками помехоустойчивости при неитеративных методах декодирования [6]. Известны также так называемые «балансные» коды Грея [2], обеспечивающие равномерную защиту бит на различных позициях.

Код Грея является наилучшим выбором при отсутствии априорной информации, то есть он оптимален для схем, не использующих итеративную обработку. В последнем случае, должен выбираться манипуляционный код, обеспечивающий не максимально возможное значение передаточной функции при отсутствии априорной информации T(dem) (0), а код с достаточным порогом первоначальной сходимости (по возможности с минимальным запасом), но обеспечивающий наилучшие характеристики после завершения итерационного процесса, т.е. максимально возможную величину T(dem) (1). Код Грея для этой цели не подходит, поскольку, несмотря на то, что для него T(dem) (0) максимально, наличие априорной информации мало влияет на увеличение взаимной информации на выходе модулятора, наклон передаточных функций на диаграмме EXIT chart мал T(dem) (1) ~ T(dem) (0) и, следовательно, итера- ционный процесс не будет приводить к улучшению характеристик.

Манипуляционное кодирование по методу SP было предложено в [3-5] для модуляции с решетчатым кодированием. Это был первый метод совместной оптимизации кодирования и модуляции. Целью была максимизация минимального евклидова расстояния между кодовыми словами.

Хорошо известно, что модуляция с решетчатым кодированием обладает плохими характеристиками в каналах с замираниями по причине малой величины кодового разнесения, несмотря на большую величину свободного евклидового расстояния. Поэтому наибольший интерес в рассматриваемой задаче будут представлять манипуляционные коды для методов модуляции, приспособленных для использования в каналах с замираниями. В частности, для bIcM и bIcM-ID.

Методы манипуляционного кодирования для систем с итеративной обработкой изучались в [715]. Наиболее известными манипуляционными кодами для итеративных систем являются MSP [8] и MSEW [10].

Критерии выбора метода манипуляционного кодирования для итеративных систем

Качественно разница в стратегиях манипуляционного кодирования в случае итеративного приема и без него может быть объяснена следующим образом. В системах с итеративной обработкой в ходе выполнения итераций появляется априорная информация об оцениваемых символах. В случаях, представляющих практический интерес, надежность этой информации возрастает по мере выполнения итераций, приближая оценки большинства бит к точным. При наличии полной априорной информации обо всех битах, за исключением оцениваемого, сигнальное созвездие превращается в bPSK, состоящее из двух точек, отличающихся значением оцениваемого бита только в одной позиции. Следовательно, для обеспечениянаилучшиххарактеристик(приболь-ших отношениях сигнал/шум), манипуляционное кодирование должно быть выбрано таким, чтобы минимальное евклидово расстояние между двумя сигнальными точками, имеющими метки, отличающимися одним битом, было максимальным. Но при выборе манипуляционного кода в схемах без итеративной обработки критерий совершенно другой: присвоить значения меток, имеющих минимальное хемминогово расстояние, сигнальным точкам с минимальным евклидовым расстоянием, или другими словами, минимизировать евк- лидово расстояние между сигнальными точками, имеющими метки с минимальным хемминговым расстоянием. В частности, целью кодирования Грея является минимизация евклидова расстояния для сигнальных точек, метки которых находятся на хемминговом расстоянии друг от друга, равном единице.

Способы формального описания манипуляционного кодирования и подход на основе метода EXIT chart

Манипуляционное кодирование, как метод отображения последовательности m бит в одну из M = 2 ^m сигнальных точек используемого созвездия, может рассматриваться как код единичной скорости, только вносящий зависимость между выходными символами без добавления избыточности. Тогда рассматриваемую схему демодуляции (BICM-ID) можно интерпретировать как декодер последовательного турбокода (SCCC), в котором роль декодера внутреннего кода выполняет демодулятор, а роль внешнего – декодер помехоустойчивого, исправляющего ошибки, кода.

Аналогия с помехоустойчивым кодом очень полезна. Можно рассматривать модулятор как сверточный код, решетка которого имеет только одно состояние. Между соседними узлами решетки возможны М параллельных переходов. Переходы могут быть охарактеризованы хеммин-говым расстоянием и евклидовым весом. Соответственно, отображение групп бит в символы, рассматриваемое как кодирование, может быть описано спектром евклидовых расстояний (EDS) и спектром хемминговых расстояний. Как и при декодировании турбокодов, EDS, очевидно, будет меняться от итерации к итерации в зависимости от априорной информации.

Как известно, в большинстве случаев (а при достаточно больших величинах отношения сиг-нал/шум – во всех) код тем лучше, чем большим свободным евклидовым расстоянием d free он обладает, и чем меньше вес, соответствующий данному расстоянию. Таким образом, аналогично задаче выбора наилучшего помехоустойчивого кода, EDS может быть использован для выбора манипуляционного кода. Однако в случае использования итеративной обработки следует учитывать зависимость EDS от количества априорной информации, поступающей на вход декодера. В первом приближении задача выбора наилучшего манипуляционного кода должна состоять в выборе его варианта, обладающего приемлемыми характеристиками, как при отсутствии априорной информации, так и при наличии полной априор- ной информации о принимаемом сигнале (знании точных значений всех бит сообщения за исключением оцениваемого).

В случае полной априорной информации EDS может быть сравнительно легко получен, поскольку выбор происходит только между двумя точками созвездия и требуется перебор всех попарных комбинаций, отличающихся оцениваемым битом.

Из аналогии с последовательным турбокодом следует, что для достижения хороших характеристик модулятор (как аналог внутреннего кода в схеме Sccc) должен был бы быть рекурсивным кодером. Но это невозможно, поскольку он (модулятор) не является устройством, обладающим памятью. Следовательно, не будет выигрыша от наличия перемежителя (interleaver gain) и достижение точки (1,1) на диаграмме EXIT chart невозможно. Однако, при помощи оптимального согласования модулятора и внешнего кода можно добиться достаточно большого значения передаточной функции модулятора в конечной точке ^T map ( 1 ) ■

Согласование модулятора и кодера внешнего помехоустойчивого кода в случае итеративной обработки сигнала на приеме может быть проведено на основе учета зависимости EDS от априорной информации [10], другим подходом может быть использование технологии EXIT chart. Поскольку взаимная информация (используемая методом EXIT chart) в отличие от EDS, зависит от характеристик канала, следовательно, они (свойства канала) учитываются при данном методе оптимизации манипуляционного кода, что должно положительно сказываться на характеристиках. Это существенное преимущество метода, основанного на EXIT chart по сравнению с аналогичным, основанным на расчете EDS [10].

С точки зрения метода EXIT chart согласование между собой модулей итеративного устройства обработки представляет собой задачу выбора соответствующей формы передаточных функций отдельных модулей, так чтобы:

• -    по возможности приблизить друг к другу передаточные функции взаимодействующих между собой модулей, поскольку площадь области между этими кривыми представляет собой величину, равную потере пропускной способности по сравнению с максимально возможной ее величиной, равной пропускной способности внутреннего модуля обработки. Отсюда следует, что избыточность, вносимая внутренним модулем обработки, должна быть по возможности меньшей. А скорость внутреннего кода ближе к

единичной. Однако, очевидно, что сужение туннеля между передаточными функциями будет приводить к увеличению числа итераций до достижения окончательных характеристик, то есть к увеличению вычислительных затрат;

• -    избежать раннего пересечения кривых передаточных функций отдельных модулей, по возможности, добиваясь достижения крайней точки (1,1) на диаграмме EXIT chart, с целью достижения максимальных характеристик после завершения итерационного процесса;

• -    для внешних модулей обработки(связанных с каналом передачи) обеспечить достаточную величину значения передаточной функции модуля при отсутствии априорной информации (в точке I pr = 0 ), с целью обеспечения гарантированной сходимости итерационного алгоритма.

Согласно «свойству площадей» последние два требования являются противоречивыми и требуют компромиссного подхода.

Для возможности удовлетворения вышеназванным требованиям модули обработки должны обладать некоторыми управляемыми параметрами (степенями свободы), позволяющими влиять на форму передаточной характеристики.

Например, в рассматриваемой задаче, управляемые параметры демодулятора – вид сигнального созвездия и тип манипуляционного кода. Пропускная способность ограничена видом созвездия, но не зависит от типа манипуляционного кода. Изменением вида манипуляционного кода можно добиваться согласования передаточной функции демодулятора с передаточной функцией внешнего помехоустойчивого кода.

Основные управляемые параметры помехоустойчивого кода – скорость и длина кодового ограничения. Скорость ограничивает пропускную способность, а изменением длины кодового ограничения можно добиваться изменения вида передаточной функции.

Три характеристики демодулятора важны при проектировании итеративных устройств обработки сигнала:

• -    значение передаточной функции при отсутствии априорной информации T ⁽ dem ) ( 0 ) , эта величина определяет порог первоначальной сходимости алгоритма, то есть она обязательно должна быть больше соответствующей величины передаточной функции декодера T ⁽ dec ) ( 0 ) ;

• -    значение передаточной функции при полной информации относительно всех бит, кроме оцениваемого определяет характеристики в конечной точке сходимости итерационного алгоритма;

• -    площадь под кривой передаточной функции, равная пропускной способности устройств

cw ^ymap\d)dd

Основное свойство передаточной характеристики манипуляционного кода состоит в том, что площадь под кривой передаточной функции демодулятора зависит только от выбранного сигнального созвездия, но не зависит от закона отображения бит в символы. Следовательно, варьируя способом отображения бит в символы можно изменять вид передаточной функции манипуляционного кода, но при этом обязательно будет существовать компромисс между T ( dem ) ( 0 ) и т(dem) ( 1 ) _: увеличение (путем выбора того или другого манипуляционного кода) одной из этих величин непременно должно сопровождаться уменьшением другой и, таким образом, уменьшение порога сходимости итеративного алгоритма будет приводить к ухудшению его характеристик после завершения процедуры. Поэтому, необходимо добиваться приемлемого компромисса между этими параметрами.

Алгоритмы построения манипуляционных кодов для систем с итеративной обработкой

Для небольших сигнальных созвездий возможен компьютерный перебор всех возможных вариантов отображения с целью поиска наилучшего. Но для больших созвездий сложность такого подхода резко возрастает, поскольку количество вариантов пропорционально M ! (необходимо ис-ключитьсимметричныекомбинацииивращения). Практически такой перебор возможен только для низкоскоростных систем передачи информации с модуляцией малой кратности. Например, для QPSKвозможнотолькодвавариантаманипуляци-онного кодирования: Грея и анти-Грея. Для высокоскоростных модемов, использующих частотноэффективные методы модуляции поиск методов манипуляционного кодирования при помощи перебора всех возможных вариантов очевидно становится неприемлемым. Так, поиск путем перебора даже при помощи компьютера невозможен для сигнальных созвездий с количеством точек больше 8 (8! = 4320, 16! = 2.09279Е13).

В [16] отмечается, что в настоящее время нет точных конструктивных методов решения данной задачи. Существуют только эвристические алгоритмы, способные с большой вероятностью найти решение возможно близкое к наилучшему. Это разновидности генетических алгоритмов [19]: «жадный» алгоритм (GA – Greedy Algorithm), TS (Tabu Search) [17], [18], и BSA (Binary switching algorithm) [20].

Данная задача относится к так называемому классу задач неполиномиальной вычислительной сложности [1 9], то есть таких, вычислительные ресурсы на решение которых не могут быть охарактеризованы полиномом степени, зависящей от размерности задачи. Для решения задач подобного рода вместо поиска его точного варианта, строго максимизирующего значение целевой функции, как правило, используются подходы, основанные на понятии «приемлемости решения» с точки зрения потребителя и строятся алгоритмы, позволяющие это решение найти. Такого рода алгоритмы, обычно, используют итеративные методы обработки, последовательно отыскивая все лучшие варианты решения до тех пор,пока качество решения не достигнет приемлемого уровня или не будет исчерпан ресурс на объем вычислений. Основная проблема при построении такого рода алгоритмов – ложная сходимость к локальному (а не к глобальному) экстремуму целевой функции. Особенно это касается вышеупомянутых «жадных» алгоритмов. Считается, что алгоритм эволюционно-генетического поиска bSA лучше других вышеупомянутых преодолевает проблему скатывания в область локальных экстремумов.

Данный алгоритм, изначально использовавшийся в задачах неравномерного квантования и примененный для выбора метода манипуляционного кодирования в [21 ], является наиболее известным и согласно [1 7] наилучшим для рассматриваемой задачи. В то же время этот метод является достаточно простым по структуре и экономичным с точки зрения вычислительных ресурсов.

В [21-22] и [16] приводятся результаты поиска с помощью алгоритма bSA подходящих методов манипуляционного кодирования для определенных видов сигнальных созвездий. Поскольку для использования в КВ модеме, по ряду причин [23], должны использоваться сигнальные созвездия, отличные от рассматриваемых в вышеупомянутых работах, то целесообразно найти близкие к наилучшим способы отображения групп бит в символы именно для интересующих видов сигнальных созвездий. Это может быть выполнено при помощи алгоритма bSA.

Краткое описание алгоритма BSA и его формализация для рассматриваемой задачи

• 1.    Случайная начальная инициализация.

• 2.    Вычисляется интегральная величина какой-либо целевой функции стоимости Е ( Т , § ) зависящая от вида сигнального созвездия Ψ и манипуляционного кода ξ . Целью является минимизация Е ( Т , § ) , то есть ищется решение ^o_Pi = arg min { — ( V , § ) } , на которое могут накладываться дополнительные условия.

• 3.    Тем или иным способом определяется вклад каждого символа (цена каждого символа) в данную функцию и создается ранжированный в порядке уменьшения величины данного вклада список символов.

• 4.    Метка первого по списку символа, последовательно заменяется меткой каждого из остальных символов. Находится вариант перестановки меток приводящий к наименьшему значению целевой функции и происходит возврат к п.2. Если в результате ни одной из перестановок меток величина целевой функции стоимости не уменьшается, то операция повторяется для следующего по списку символа.

• 5.    Алгоритм выполняется до тех пор, пока либо не перестанет уменьшаться значение целевой функции, либо не закончится лимит времени на проведение вычислений.

Алгоритм находит локальный минимум функции стоимости. Однако, если алгоритм выполняется несколько раз, проинициализированный случайным образом, то с большой вероятностью может быть найден глобальный минимум [16]. Критерием качества решения может служить относительная частота его нахождения при различных случайных инициализациях алгоритма. Строгого формального доказательства оптимальности выбранного решения нет.

Построениецелевойфункциистоимости для алгоритма BSA

Ключевыми моментами bSA алгоритма являются способ построения целевой функции стоимости и критерий ранжирования списка сигналь-ныхточекповеличиневкладавцелевуюфункцию. В [22] предлагается проводить поиск оптимального вида манипуляционного кодирования при помощи алгоритма bSA, используя построение целевой функции стоимости и проводя ранжирование списка сигнальных точек на основе EDS. Поскольку в рамках рассматриваемой задачи нас интересуют созвездия, используемые в КВ моде- мах передачи данных [25-28], являющиеся неэквидистантными, и, следовательно, для которых описание при помощи EDS не совсем подходит, а также, желая принять в расчет характеристики канала связи, предложим другой подход к выбору целевой функции стоимости на основе взаимной информации и метода EXIT chart [7].

Формализуем требования к Е ( Т , § ) и уточним дополнительные условия, накладываемые на ξ , для предлагаемого подхода.

Условие достижения максимальных характеристик в конечной точке сходимости может быть получено на основе следующих соображений. Пусть I ^' есть результат решения уравнения T demap ( ¹ ) = ^T d - Cod ( ¹ ) , то есть абсцисса точки пересечения кривых передаточных функций. Естественной характеристикой качества манипуляционного кода является значение вероятности ошибки после завершения итерационного процесса p _BER . Эта величина однозначно определяется значениями априорной I _pr и внешней I _e информации на входе и выходе завершающего модуля обработки на последней итерации его работы. Соответствующая зависимость p BER ( I _pr , I e ) может быть рас-считанааналитически,измеренаэксперименталь-но или получена при помощи моделирования.

С этой точки зрения наилучшим выбором манипуляционного кода будет:

• ^ opt = argmax { T demap ( I ) } , (1) ξ

а в качестве интегральной целевой функции алгоритма bSA следует выбрать:

E ( T , § ) = -T dema, ( I ) . (2)

Знак минус необходим, поскольку оптимизация в алгоритме bSA рассматривается как задача минимизации целевой функции E ( T , § ) .

Если внешний помехоустойчивый код является достаточно мощным, например, используется турбокод, LDPc код или сверточный код с большой величиной кодового ограничения, то передаточная характеристика декодера в области значений априорной информации, приближающихся к единице, будет плотно «прижатой» к вертикальной асимптоте I _pr = 1 . Тогда характеристики алгоритма после завершения итерационного процесса будут определяться в основном свойствами демодулятора, поскольку его характеристики в конечной точке, как правило, гораздо дальше отстоят от своего предельного значения, чем характеристики декодера, то есть для конечной точ-

Idemap        demap ppr Р) >> Ie p) или, (decod )        (decod )

что то же самое, I p ' <<  I e \ При таком условии, близким к наилучшему будет следующий выбор вида манипуляционного кодирования § :

S ept ~ arg max { T demap ( 1 ) } = arg max { I m -i } , (3) для которого целевая функция алгоритма bSA должна быть выбрана как

• 2 ( V, § ) = - T dema, ( 1 ) = — I m- , (4) что гораздо проще для вычисления, чем (2).

Но в таком случае (при замене критерия выбора (1) на (3) и целевой функции алгоритма bSA (2) на (4)) необходимо гарантировать отсутствие других точек пересечения кривых передаточных функций демодулятора и декодера при I существенно меньших I .

С этой целью сформулируем следующее условие, которое также может рассматриваться как условие первоначальной сходимости, по анало^гии с условием T demap ( 0 ) decod ( 0 ) в [22]:

min { T d„ap ( I ) — ^TdL ( I ) } >^ - (⁵⁾

Величина 0 < A <<  1 представляет собой некоторый запас надежности, обеспечивающий достаточную ширину тоннеля и влияющий на количество итераций. Участок поиска минимума функции может быть ограничен интервалом 0 <  I <  R (где R - скорость внешнего кода), а не 0 <  I <  1 - так как передаточная функция декодера является выпукло-вогнутой с точкой перегиба при I = R .

Рассмотрим взаимосвязь предлагаемого подхода с задачей оптимального согласования по пропускной способности методов модуляции и кодирования. Условием такого согласования с точки зрения подхода на основе взаимной информации является минимизация выражения:

• ¹    m - 1 min ^ J^T demap ( I ) — T Cod ( I ) ]dI ^ min ^ E I f " (6)

" 1 0 I "  I i = 0 J

Согласно вышеупомянутому «свойству площадей» передаточной функции демодулятора, выполнение (3) автоматически влечет удовлетворение (6). Поскольку условие (3) проще для проверки, то выбрать следует его, при этом оптимальное согласование будет достигнуто автоматически.

Начальная инициализация алгоритма BSA

Условие (5) с наибольшей вероятностью выполняется для кода Грея, но при этом характеристики в конечной точке сходимости будут наихудшими. Максимальная величина T _demap^ ( 1 ) (условие (3)) получается для манипуляционного кода анти-Грея, но при этом может не выполняться условие (5).

Если одно из условий (или оба сразу) выполняется с некоторым запасом для крайних случаев (кодов Грея или анти-Грея), то может быть найден лучший вид манипуляционного кодирования: либо с меньшим порогом первоначальной сходимости (сдвиг в сторону кода Грея); либо с лучшими окончательными характеристиками (сдвиг в сторону кода анти-Грея).

Если первоначально не выполняется ни одно из условий (каждое для своего крайнего случая), то решение не может быть найдено и требуется выбор другого внешнего помехоустойчивого кода большей скорости.

Когда оптимальное решение существует, оно может быть найдено с помощью алгоритма bSA как ^o t = arg min {E (T,^)}. В качестве целевой p          ξ функции Е (Т, §) выгодно использовать (4) при дополнительной проверке условия (5).

Предлагаемыйкритерийранжирования сигнальных точек для алгоритма BSA

Критерий переключения пар в алгоритме bSA требует расчета вклада каждого символа в итоговое значение целевой функции. В [22], где предлагается схожий вид целевой функции, так же основанный на взаимной информации, данный критерий строится при помощи расчета спектра евклидовых расстояний манипуляционного кода. Как уже упоминалось, этот подход затруднительно реализовать для неэквидистантных сигнальных созвездий, поэтому предложим вариант, основанный на символьной взаимной информации. В качестве критерия ранжирования списка будет выбираться величина отклонения символьной передаточной характеристики от значения передаточной характеристики внешнего помехоустойчивого кода при I = 1 - то есть T (1|xi). Расчет передаточной функции демодулятора как для каждого символа, так и в среднем может быть произведен аналитически или при помощи моделирования его работы. Достоинством экспериментального измерения передаточной функции является автоматический учет погрешностей реализации алгоритмов обработки. Однако в данной задаче его трудно использовать по причине больших вычислительных затрат.

Вывод аналитических выражений для безусловной и условной передаточных функций демодулятора

Вместо экспериментального определения передаточной функции демодулятора на символьном уровне (то есть зависимости взаимной информации на выходе от взаимной информации на входе для символов) для нее может быть получено аналитическое выражение на основе следующего подхода.

В [29] был предложен метод описания систем с многопозиционной модуляцией на основе взаимной информации и концепции эквивалентных каналов, согласно которой взаимная информация I (Y, X) о передаваемом символе сообщения X , после приема сигнала Y , соответствующего данному передаваемому символу, может быть представлена как:

m-1

I (Y, X) = £ I i ,              (7)

i = 0

где I l – средняя взаимная информация, приходящаяся на бит передаваемого сообщения, при условии, что точно известны другие l бит из m бит символа. Усреднение производится по всем возможным значениям числа известных бит l (от 0 до m - 1 ); а также m позициям бита в символе; C _m ^l _-1 конфигурациям известных бит и 2 ^l комбинациям значений известных бит. В итоге получим:

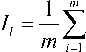
C ^l

1- 1 ? 1 1 (M c l ⁾ ) , m-1 j = 1 ² Cj ^X           ’

где c j ) — j -й вариант одного из C m -1 векторов априорно известных l бит, а условная взаимная

I ( ^Y , C i |c jl ¹ )

информация

рассчитывается непос-

редственно по определению

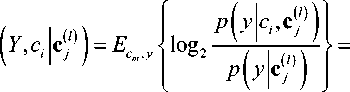
Л

= 2 1 f P ( У\^С‘’ c j ) )

² C i = { 0,1 } 4                '

X log 2

² P ( y\ ^ci, c j ) )

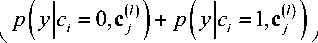
dy . (9)

В свою очередь, условная плотность вероятности сигнала на входе p (y|c;, c()), зависящая от вида сигнального созвездия Ψ и манипуляционного кода ξ рассчитывается путем усреднения ус- ловной плотности вероятности входного сигнала p(y|x) по 2m-l-1 точкам сигнального созвездия x, имеющим значения cj на l позициях точно известных бит и значениям бита ci на i -ой по- зиции

p

( y\ci, c l ) ) = TmUr   1 p ⁽ yx ) ,   ⁽¹0)

X     ' 2   x^j где p (y|x) представляет условную (при условии, что передавался символ x) плотность вероятности сигнала на входе демодулятора приемника, которая всегда может быть легко получена, если известна статистика помех и замираний в канале. Например, для канала АГБШ

— Р ( yx ) = ^ex P

{| y - x| ² /сn ² } / 2 nc П и для канала с

независимымизамираниямииплотностьювероят-ности распределения амплитуд pr (^) и АГБШ -∞ p (yx) = JPr (s) exp {| y - sx 2 A2} ds/:

2 πσ _n ² .

Для самых интересных случаев, отсутствия ( l = 0 ) или наличия полной ( l = m - 1 ) априорной информации, вычисления по (10) довольно просто могут быть выполнены, так как Т ( c i , c ( j ) ) представляет собой множество либо всех точек сигнального созвездия Ψ _, либо сводится только к двум точкам, отличающимся значением неизвестного бита соответственно.

Величина I (Y, X) зависит только от вида используемого сигнального созвездия Ψ , но не зависит от вида манипуляционного кода ξ , несмотря на то, что I ₀ , I ₁ ... I _m-1 зависят от ξ . Очевидно, что I ₀ ≤I ₁ ≤ I ₂ ≤... ≤I _m-1 .

Величина I0 – средняя по всем позициям величина взаимной информации на бит сообщения символа при отсутствии априорной информации о других битах символа. Параметр Im-1 – средняя величина взаимной информации в бите символа сообщения, усредненная по всем позициям, при известных значениях бит на всех остальных m - 1 позициях, кроме позиции оцениваемого бита, и определяет характеристики при полностью известной априорной информации, то есть в конце итерационного процесса.

Очевидно, что       I 0 = T ^{( demap )} ( 0 )       и

( demap )

Im-i = T     (1). Так же несложно показать, что II = T( emap) (1/(m -1)). Следовательно, T(demap) (i) легко может быть определена в точках I = i/(m — 1), i = 0 ... m -1.

Методы приближенного вычисления передаточной функции демодулятора

Интересный вариант приближенного вычисления передаточной функции демодулятора был недавно предложен в [30]. Определяется эквивалентный виртуальный дискретный канал с жесткими решениями по символам, обладающий такой же пропускной способностью, как и непрерывный канал (с АГБШ или замираниями) и для него по простой формуле для дискретных каналов [7] вычисляется передаточная функция демодулятора. Как утверждается в [30], она является хорошей аппроксимацией передаточной функции демодулятора с мягкими решениями по каналу обратной связи.

Результаты поиска оптимальных манипуляционных кодов и их анализ

При помощи разработанного подхода были найдены оптимизированные манипуляционные коды для сигнальных созвездий 16QAM, 32QAM и 64QAM, предназначенные для модемов КВ диапазона [25-28]. Поиск проводился путем многократных независимых попыток использования процедуры bSA со случайной начальной инициализацией. Целевая функция выбиралась в соответствии с (3), при ограничении на решения (5). Окончательно выбирался результат с лучшими характеристиками.

При выборе манипуляционного кода для 16QAM для каждого набора параметров проводилось около 100 независимых попыток поиска лучшего решения при случайных начальных параметрах. Примерно в 15% случаев остановка алгоритма происходила в результате прекращения уменьшения величины Е ( Т , § ) . Примерно в 40% указанных случаев решения совпадали, и при этом величина Е ( Т , § ) была наименьшей из всех рассчитанных в ходе всех экспериментов. Согласно [22], это является удовлетворительным результатом, свидетельствующим о высокой вероятности нахождения глобального минимума ^Е ( Т § ) .

Для 32QAM выполнялось около 50 независимых попыток поиска лучшего решения. Остановка алгоритма в результате насыщения происходила примерно в 4% случаев. Случаи совпадающих вариантов решений были единичны.

Для 64QAM осуществлялось около 30 вариантов поиска для каждого набора параметров. Во всех случаях остановка алгоритма происходила по истечении лимита времени на вычисления. Совпадающих решений получено не было.

Несмотря на то, что для созвездий 32QAM и 64QAM оптимальное решение, очевидно, не было получено, характеристики найденных заметно превышают аналогичные показатели для известных или случайно выбранных вариантов решений.

Помимо алгоритма bSA, выбор наиболее подходящих вариантов проводился при помощи ненаправленного случайного поиска. Интересно, что последний путь, позволяя добиться характеристик выше средних, не приводил к столь хорошим результатам как bSA за сопоставимое время вычислений.

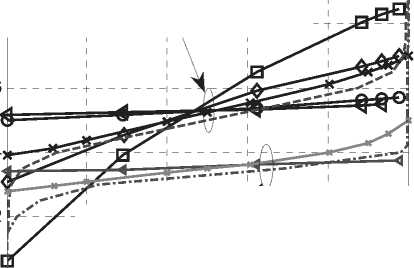
В качестве примера, на рис. 1 изображены передаточные функции демодуляторов для известных и оптимизированных, согласно (3) и (5), способов манипуляционного кодирования для сигнального созвездия 16QAM, используемого в КВ модемах [25-28]. Предложенные способы предназначены для сочетания модуляции:

• -    со сверточным кодом (133,171), R = 1/2, декодируемым с помощью алгоритма SOVA при E b[ N 0 = 1 dB ( SNR = 7,021 dB );

• -    с турбокодом, R = 1/3, декодируемым алго-ритмомBCJR-MAP,15итерацийи E b /N ₀ = -2 dB , ( SNR = 4,021 dB ).

0.8 0.6 0.4

На рис. 1 приведены так же обратные передаточные функции данных декодеров, образующие диаграммы EXIT chart. (Поскольку декодеры являются внешними модулями, их передаточные функции не зависят от величины отношения сигнал/шум.) Как видно из рис. 1 предлагаемые методы манипуляционного кодирования обеспечивают меньшую величину порога сходимости при большем значении передаточной функции в конечной точке.

Как видно из рис. 1, оптимизация манипуляционного кодирования позволяет заметно улучшить согласование кода с модуляцией, выражающееся в уменьшении потерь пропускной способности (численно равных площади тоннеля между кривыми передаточных функций) из-за необходимости уменьшения скорости кодирования. А также улучшает характеристики алгоритма, определяемые значением передаточной функции в конечной точке, при приемлемом снижении порога первоначальной сходимости и отсутствии преждевременного пересечения кривых передаточных функций. Видно, что для сверточного кода, при вышеназванных условиях, добиться сходимости итерационного алгоритма можно только при оптимизированном манипуляционном коде.

свёрточный код, R=1/2,

Eb/No=1 dB, (SNR=7,021 dB)

турбо код, R=1/3

Eb/No=-2 dB, (SNR=4,021 dB)

0.2       0.4       0.6       0.8

i (map) pr

Gray

Anti-Gray

Natural

MIL-188-110B (1 dB) оптимиз.манип. код для свёрт.кода свёрт.код (133,171)

MIL-188-110B (-2 dB) оптимиз.манип. код для турбо кода турбо код, R=1/3

Gray, свёрт. код оптимиз. манип.код для свёрт. код

Gray, турбо код оптимиз. манип. код для турбо кода

Рис. 1. Диаграммы EXIT chart для различных манипуляционных кодов

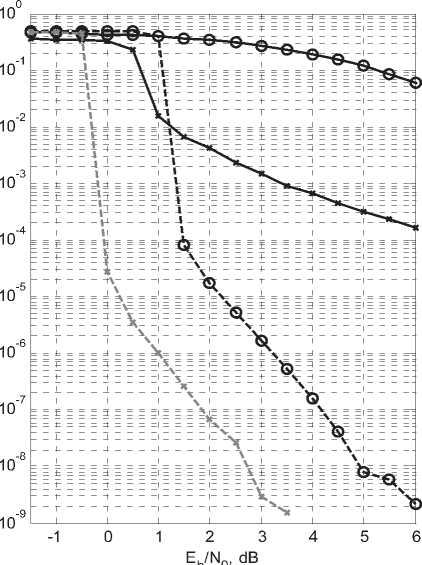
Обратной стороной хорошего согласования является замедление процесса сходимости, проявляющееся в увеличении необходимого количества итераций для достижения конечной точки, и, соответственно, в увеличении вычислительных затрат. Так, для изображенного на рис. 1 случая, конечная точка для стандартного по [28] манипуляционного кода может быть достигнута за одну-две итерации, в то время как для оптимизированного кода требуются семь – восемь итераций (но, как видно на рис. 2, величина двоичной ошибки в результате оптимизации может снизиться более чем на два порядка!).

На рис. 2 показаны зависимости вероятности ошибок от величины отношения сигнал/шум для описанных выше случаев различных типов сигнальных созвездий, включая предложенные. Величина энергетического выигрыша достигает 2 дБ для турбокода, что согласуется с [22], где так же методом bSA, но при другом выборе целевой функции и способах ранжирования точек решена аналогичная задача для QAM созвездий прямоугольной формы.

Рис. 2. Зависимости bEr от отношения сигнал/шум для различных манипуляционных кодов

Выводы

• 1.    На основе использования технологии EXIT chart разработан метод оптимизации манипуляционного кодирования при итеративной обработке сигнала. Достоинством метода, по сравнению с другими известными, является учет характеристик канала связи.

• 2.    При помощи разработанного подхода получены оптимизированные манипуляционные коды для сигнальных созвездий, стандартно используемых в КВ модемах передачи данных, при разных методах помехоустойчивого кодирования (включающих как простые сверточные, так и турбокоды).

• 3.    Для рассмотренных видов сигнальных созвездий найденные манипуляционные коды с высокой вероятностью являются наилучшими из возможных, а для созвездий с большей частотной эффективностью (с большим количеством сигнальных точек) обеспечивают заметное улучшение характеристик помехоустойчивости.

• 4.    Результаты моделирования демонстрируют величину энергетического выигрыша пред-

• лагаемого метода около 2 дБ по сравнению с кодом Грея.

Работа выполнена при финансовой поддержке РФФИ (проекты 08-02-13555, 09-07-97522).