Many-parameter m-complementary Golay sequences and transforms

Binary ± 1-valued Golay – Rudin – Shapiro sequences (2-GRSS) associated with the cyclic group Z2n were introduced independently by Golay [1, 2, 3] in 1949-1951, Shapiro [4, 5] and Rudin [6] in 1951.M.J.E.Golay [2] introduced the general concept of “complementary pairs" of finite sequences all of whose entries are ± 1. For building the classical FGRST in bases of classical 2-GRSS the following actors are used: 1) Abelian group Z2, 2) 2-point Fourier transform ^2, and 3) complex field С, i.e., these where {Grm,Gr2,...,Grm} is a set of arbitrary finite groups of given order m Here {Um, Um,..., U m} is a set of arbitrary unitary (m×m) – transforms represented in the many-parameter Jacobi-Euler form [9– 10]:

m — 1    m

um = um (фо, ф1,..., ф^ )=um (ф^ )=п П J (ф’г , s), r=1 s=r+1

m—1   m um = u m(фo2, ф?,..., ф2 )=um (фq)=пп J(ф 2, s), r=1 s=r+1

transforms are associated with the triple ( Z 2 , ^ 2 , C ).

In previous papers [7, 8], we have shown a new unified approach to the GF ( p ) -, or Clifford-valued complementary sequences and Golay transforms. It was associated not with the triple ( Z 2 , ^ 2 , C ), but with triples

( Z 2 , { CS 2 ( ф 1 ,a_b Y i ), CS₂ 2 ( ф ₂, « 2 , у 2 ),...,

CS П ( ф „ , a „ , у n ) } , A lg )

and ( Z 2 ,CS₂( ф , a , y ), Alg ) , where { CS 2 ( ф 1 ,a_b Y i ),

CS₂ ² ( ф ₂, a ₂, Y 2 ),..., CS П ( ф _n , a _n , y _n ) } is a set of arbitrary

unitary(2×2) -transforms of type

CS₂( ф k , a k , Y k ) =

e i ^{a k} cos ф _k e ^— i ^{Y k} sin ф _k

e i^k sin ф _k

- e ^{- i a k} cos ф _k

,

k = 1,..., n, and CS2 (ф, a, y) is a single transform, Alg is an algebra (for example, Clifford algebra).

In this work, we develop a new unified approach to the so-called generalized multi-parameter m – complementary sequences. This construction has a rich algebraic structure. It is associated not with the triple ( Z ₂, ^ 2 , C ) , but with

• 1)    ( Z m , U m , Alg ) , 2) ( Z m , { u m , u m ,..., U m } , Alg ) ,

• 3)    ( Gr m , { u m , и m ,..., и m } ,Alg ) ,

• 4)    ( { Gr m , Gr m ,..., Gr m } , { u m , u m ,..., u m } , a lg ) .

n

m

where

= u m ( ф о , ф О ,

is the Jacobi

...

m — 1 m

, ф q ) = u m ( ф q ) = ПП J ( ф ns ) ,

r = 1 s = r + 1

r

s

s

r

^J ( ф r ,s ) =

r 1 -	0		0	- 0 "
0 -	c ( ф r , s )		s ( ф r , s )	- 0
0 -	s ( ф r , s )		- С ( ф r , s )	- 0
v 0 -	0		0	- 1 ^

, orthonormal rotation with reflection,

,...,

ф^ = (фо, ф1,..., фq),..., ф q = (фо, ф,

parameters, q = C m = m ( m — 1) / 2,

ф q ) are the Jacobi c ( ф r , s ) = cos ( ф r , s ),

s ( ф r , s ) = sin ( ф r , s ).

The rest of the paper is organized as follows: in Section 2, the object of the study ( Golay – Rudin – Shapiro m -ary sequences) is described. In Section 3 we propose method based on new generalized iteration rule with n unitary ( m × m )-transforms U ¹ _m , U ² _m ,..., U ⁿ _m and single group Z m . Then we generalize the previously method on n unitary ( m × m )-transforms U ¹ m , U ² m ,..., U m ⁿ and on n finite groups { Gr m , Gr 2 ,..., Gr m, } - In Section 5 we derive fast algorithms for binary Golay transforms.

The object of the study.New iteration construction for original Golay sequences

We begin by describing the original Golay m -complementary sequences.

Definition 1 . A generalization of the Golay complementary pair, known as the Golay m-Complementary m-element Set (m- GCS ) of complex-valued sequences [11]

como(t) := (co(O), co(1), ..., co(m -1)), m-GCS = (

com i ( t ) : = ( C i (O),    C 1 (1), ..., c 1 (m - 1) ) ,

....................................................................., com m-1 (t) := (cm-1(0), cm-1(1),..., cm-1( m -1))

is defined by m ^ COR k ( t ) = m -5 ( t ), m -1| COM 1 ( z )| 2 = m , k =0                              k =0

where {CORk (t)}m=0 are the periodic autocorrelation functions of {comk (t)}m=1 and COMk (z) = Z {comk (t)} are their Z - transforms.

We use two symbols ane[0,mn-1-1] = Zmn and tne[0,mn-1-1] = Zmn for numeration of Golay sequences and discrete time, respectively. For integer ane[0, mn-1-1] = Zmn and tn€'0, mn-1-1] = Zmn we shall use m-arycodes     an = (a1,a2,...,an), tn = (t1,t2,...,tn), where a1t1e{0,1,^,m-1} = Zm, i=1,2,...,n.

Let an = (a1,a2,...,an) and tn = (t1,t2,...,tn) be m-ary codes, then define an = |an| = Aan-i+1 mi-1, and tn = |tn| = A tn_м mn-i i =1

as integers whose m-ary codes are an = (aba2,...,an) and tn = (t1,t2,...,tn), where an, t1 are less significant bits (LSB) and a1, tn are most significant bits (MSB) of a n = (a1, a 2,..., a n) and

Obviously, a1 = (a1) € Zm, a2 =(61,a2)€Zm xZm = Z2, a 3 =(a 2, a3 )€ Zm x zm = zm, ,

an = (an-1, an) € z m1 x zm = zm t = (t1 ) € Z m , t2 = ( t1, t2 ) € Zm X Zm = Zm , t3 = ( t2, t3 ) € Zm X Zm = Zm ,

( t ₁, t ₂,..., t_n ) , respectively.

a 1 = a € Z m ,

( a_b a ₂ ) € Z m X Z m , ( a ₂, a 3 ) € Z _m 2 x Z m ,

.............................,

( a n -1 , a n ) € Z - 1 x Z m ;

t 1 = t 1 ^{€ Z} m ,

( t 1 , t 2 ) ^{€ Z} m ^{x Z} m ,

( t 2 , 1 3 ) € Z _m 2 x Z m ,

...................................................., ..........................., tn =( t„-1, tn )€ Zm. x Zm = Zm ,     (t n-1, tn )€ Z mn., x Z m .

Let {com^n^(tn+1)} be mn+1-element set of m complementary sequences (of length mn+1), where an+1, tn+1 = 0,1,.., mn+1-1 They form rows of a (mn+1Xmn+1) -matrix G[n„+1] = Г com,n+1](t„+1)!         , that is called the m +1      L        an+1     n+1 7_lan+,.tn+, =0, m-Golay matrix. Here index [n+1] shows that Golay matrix have been obtained on the n+1 iteration step. We are going to group these rows (sequences) as mn+1 -1

com

[ n +1]

( a n + 1 )

^a n + 1 =⁰

( t n +1 )

^ m -1                          A m n -1

Ecom' a+1an+,)(t n+1) = EE y_a n+1 =0                          / a n =0

Let us to select the more fine structure of the m -Golay matrix:

com ' n a + '0)^{( t} n +1 ) com ' n a + j])^{( t} n +1 )

. com ( ⁿ a + m -1) ( t n +1 )

^com( "a + - ¹₁^]0,0)^{( t} n +1 )

com ' 21’0,1) ( t n +1 )

m n + - 1                              mn-1 c ' n +1] — 1 1 1 ——' n +1]      \ _ lll G m n + 1 = r"E com( a n + 1 )( t n +1 ) = rE	com ' n a + '0)( t n +1 ) com ' n a + 11])( t n +1 )	m n -1 -1 = ffl	r m -1 E	com ' 2А ^^ n +1 ) com( a +A n 1)( t n +1 )	>	m n - 1 -1 = в
a n + 1 =0                           a n = 0	..................... . com ' "a + m -1)( t n +1 ) .	a n - 1 =0	" ■ =0 V	...................... _ co m ( n a +A n m -1)( t n +1 ) .	V	a n - 1 =0

com ' n a +A. m -1)^{( t} n +1 ) com ' n a + - i t n +1 ) com ' A , ^]1,1)^{( t} n +1 )

...

com ' n a +A, m -1)^{( t} n +1 )

com ' n a +A-1,0)^{( t} n +1 ) com ' n a +¹’ m -11)^{( t} n +1 )

com ' a +A-1 m -1)^{( t} n +1 )

Example 1. For n = 1 and n =2 we have, respectively,

G 31 1 ] =[ ^c °m a ¹ ₁ ^] ( ^t 1⁾ ] _{a 1}, _{t 1}=0 = й com a ] ( t i ) = a i =0

2 rcom(2a],0)(t 2) 1 G32] = Й com(a],1)(t 2) = a1=0 _com(a],2)(t2)_ com(20]0)(t 2) com(20]1)(t 2) com(20]2)(t 2) . □ com(2,]0)(t 2) com(2]1)(t 2) com(2]2)(t2) com(22]0)(t 2) com(2]1)(t2) _com(2,2)(t 2) _ com[(0]) (t1) com[(11]) (t1) com[(2]) (t1)

The matrix G ^[ _m ⁿ „ + ! ^] is constructed by an iteration construction. The initial matrix G ^[ _m ¹ 1 ^] is formed by starting with an arbitrary unitary ( m×m )-matrix (in manyparameter form or not)

U m = A0(0) [Aa (t)] := A0(1) G[1] = m1 A0(2) . com01](t1) com[11] (t1) n -1) .............. comm-1 (t1)_ ...    A0( A1(0) A1(1) A1(2) ...    A1(m - 1) A2(0) A2(1) A2(2) ...   A2( m - 1) ... Am-1(0) Am-1(1) Am-1(2) ...              . ...   Am -1( .. m -1) where A„ (t) e A 1g, coma] (t) = (A (0), A^ (1),..., ,L (m -1)).

Example 2 . The initial matrix G ^[ _m ¹ 1 ^] can be the Fourier transform on Abelian group Z m :

G ^[1] = m ¹

com ^[ ₀ ^1] ( t 1 )

com₁ ^[1] ( t 1 )

com ^[ ₂ ^1] ( t ₁ )

. com m L1 ( t 1 )

1	1	1.	.. 1
1	б 1 ' 1	б 12      .	..       б 1( m -1)
1	б 2 ' 1	б 22     .	о 2-( m -1) .. б

1     _c ( m -1)-1      q( m -1)'2            _c( m -1)'( m -1)

1 Б Б ... Б

where б _m = m 1 e A 1g , com ¹ , '¹ (t ) = ( 1, б ^k '1 , б ^k '2 ,..., б ^k '^{( m} 1) ) , ( k =0,1,., m -1) are characters Z m . □

It is easy to check that

(|COM o ( z )|² + |COM 1 ( z )|² + ... + |COM m -1 ( z )|² ) z ₁ = m .

Indeed, m-1                , m-1               

ZlCOMk(z)| =ZCOMk(z)COM (z) = k=1

m -1 Л m -1          Л ( m -1

= Z | Z a k ( t ) z Z a k ( * ) z¹

k =1 V t =0           7 V s =0

m-1 m-1 ( m-1               A          m-1 m-1

= ZZ| Zak(t)a(S) Izz =Z£31-z   = ZIz|2t, s=0 t=0 V k=0               J          s=0 t=0

m -1

since Z a k ( t ) a k ( s ) = 3 ₁ - _S is true for an arbitrary unitary k =0

(orthogonal) matrix. Hence,

( m -1                 A         ( m -1

|ZI COMk (z )2|    =|ZI z2 t

^V k =¹                  У_м =1 V t =0

and initial sequences in the form of rows of an unitary matrix (in particular case, in the form of characters com k ( t 1 ) = (1, б ^k ' ¹, б ^k ' ²,..., б ^k ' ( ^{m -1)}) of cyclic group Z m ) are the Golay m -complementary sequences.

Methods

The matrix Gm^1 is constructed by an iteration construction rj2                               [13       rjn+1

U _m U _m U _m

G m 1 ( U m ) ^ G m ] ( U m , U² , ) ^ .... ^ С^Ш ,..., U m , U m ⁺¹ ), (4)

where wn+1 :={um,..., um, u m+1} = {Wn, иm+1}, Wn :={Um,...,иm}.

Here U m ( ф q ) = [ A a ( 1 1 Ф q ) ] m t =0 e SU (A 1g , m ) ( s = 1, 2,…, n ) are a sequence of unitary many-parameter ( m × m ) -transforms, belonging to the special unitary group SU(Alg , m ), where s =1,2,., n +1 and A q ( 1 1 ф q ) are Alg- valued many-parameter sequences.

Let us assume that we have m -Golay matrix G ^[ m ,^]( U 1 ,..., U n ) = G m ⁿ n ^](W n ) (depending on n previous transforms U ¹ m ,..., U ⁿ m ). We need to construct the next m -Golay matrix G m ⁿ :1^] ( U m ,..., U n ⁺¹ ) = G ^[ m +!^] (W „ +1 ) using only G m ] ( U m ,..., U m ) and U m ⁺¹. We are going to use for m -Golay matrix G m n ¹ (W _n ) the same structure as in (1):

m n -1

G m ](W n ) = ffl com ( a n ) ( t n\U „ ) = ^a n =0

mn -1

= ffl

a n = 0

com ' a n -1 ,0)⁽ t n \ ^w n ) ^com( a n -1 ,1)⁽ t n \ ^w n )

com S a n -1 , m -1)^{( t} n \ ^W n )

For constructing G[mn„+!](Wn+1) from G[m„1(Wn )we take each complementary set in the form m -GCS[ n ] (Un ) =

^com( а П - 1 ,0)^{( t} n I ^U n ) com ( a n - 1 ,1) ⁽ t n ^{1 U} n )

com a n - 1 , m -1)^{( t} n | ^U n )

and construct m shifted versa of their components

/ m -GCS [ ⁿ i ( U n ) ^

X where

m -GCS a n '=0 ( U n . ) , m -GCS^ ( U n . ) ,

m -GCS L n n l m -1 ( U n +1 ) ,

p a n m

^co m ( a n - 1 ,0) ⁽ t n | ^U n ) com al 1 ,1)⁽ t n | ^U n )

com ( a +10) ⁽ t n +1 | и +1 ) com a + ^( t n+1\Un +1 )

^y (6)

^com( a n - 1 , m -1)^{( t} n ^{1 U} n )

^co m ( a +¹ m -1)⁽ t n +1 \ ^U n +1 )

Here a _n = 0,1,..., m - 1, P m a n is the cyclic permutation

operator on a n positions (modulo m ), T tm " ^s is the shift op-

erator on mⁿs positions T m"^sf ( t _n ) : = f ( t _n + mⁿ s), P m is

transposed matrix of P m .

According to (1) we obtain

com

mⁿ -1

G [ _m ⁿ :1] ( и n +1 ) = щ

n

=0

x

com

_(a+'0) ( t n + 1 \ u n +1 )

*(a+ n + 1 \ u n +1 )

^co m ( a +¹ m -1)⁽ t n +1 \ ^u n +1 )

I t n

A

mⁿ -1

Штт n +1

^a n =0

com

com

com ^[

P a,

m

n

•

T 1 m' t _n

n

T ( m - !) • m n t _n

—w

. P a n m

x (7)

- 1 ,0) ^{( t}

- 1 ,1) ⁽ t

n - 1

I U n ) I U n )

( t n \U n )

,

and, consequently, com(a+11] an ,an+1)(t n+1\Un+1) =

= У an ⁺¹ (₽„ ) T ^m" ^(P n ^ea n ) com [ n ^] _B ,( t„ \ U„).

/      a n + 1 v r n/ t n                     ⁽ a n - 1 , p n )\ n I n/

P n =0

Since t n +1 = ( t n , t n +1 ), then believing t n +1 = a n ®P n , we

m obtain:

c ^om( a n- ^a n ,a„ 1 ) ^{( t n +1} \ ^U n ⁺¹ ) ^co m ( a n - ^a n ,a„ 1 )^{( t n} , t^{n +1} \ ^U n ⁺¹ )

m -1

= Z <1 (an ®tn+1)TT" 1com[an„an®,„ +)(tn \ U„) = (8) tn+1=0              m                               m m-1

= Z Aan+1(an ® tn+1)ТГ"+1com(an-1,an etn+ 1)(t n + mntn+1 \ Un ). mm tn+1 =0

So, com( a+']an,a n+1)(t n , tn+1 \ Un +1) =

= ^A a+1 ^{( a} n ^e t n +1 ) • ^com( a П - ,a n e t n + 1 ) ^{( t} n \ ^U n )- m m

It is finally recurrent relation between m -complementary sequences of G ^[ _m ⁿ „ ⁺J^] [ U n _{+ 1} ] and G m n ¹ [ U n ] . From (9) we obtain expression for com a n n + 1 ^1] ( t _{n + 1} \ U n _{+ 1}):

n com(a+11])(tn+1)=nAaa+a ets+2(ase ts+1), a0, tn+2=0.(10) mm s=1

In particular, for matrices in the form of the Fourier transform U m = U ² _m = ... = U mm = [ s mt ] we have

com ^[”^+1]„ „ ,( t„ ₊₁) = com ^[ n ^+1]„ „ ,( t„ , t „₊,) =

^{( a} n - 1 ^,a n ^,a n + 1^{)V n + l 7              ( a} n - 1 ^,a n ^,a n + 1^{)V n} , ^{n + l 7}

Z (a s e t s + 1 ) ( a s + 1 e t s + 2 )

mm

= F s = 1

^s m .

Where « 0 , t n +2 ^ 0. New sequences in (9) are orthogonal and m -complementary sequences.

Generalizations

In this section, we introduce generalized m -complementary sequences. It is based on using new permutation matrices P m a n in (7). The mappings g : X ^ X of a set X into (or onto) itself are of particular importance. They form the following set X^х : = { g \ g : X ^ X }.

Definition 2. One-to-one map from a set X to itself g : X ^ X , x ‘ = g ( x )= g ° x is called a transformation of the set X.

If X is finite and consists of m elements (for example, X = {0, 1, 2,…, m }) then a transformation of the set X is called a permutation. As is well known, the set of all permutations of X forms a group S m = Sum { X } in which the product on of a pair of permutations ст, n is defined by ( an )° x : = o °( n °x).

If X contains more than two elements, S m is not commutative. Any subgroup of S m is called a permutation group on X , or a group of permutations of X . We shall say that the permutations in Sym (X) act or operate on the elements of X .

Definition 3. A homomorphism of a group on a set h: Gr ^ Sym { X } is called a permutation representation (or realization) of .

The image h ( Gr ) c Sym { X } is a permutation group and the elements of are represented as permutations of . A permutation representation is equivalent to an action of on the set : To specify an action, we need to define for element g e Gr the corresponding permutation h ( g ) of , that is, h ( g )° x for any x e X . We are going to write h ( g )° x

in the short form g ° x and to call the group of transformations of . The pair {) is called a space with transformation group the elements x e X are called points of the space .

Definition 4. If is a permutation group of degree , then the permutation representation of is the linear permutation representation of : P : Gr ^ GL m (Л ig ) which maps to the corresponding permutation matrix P ( g ) , .

That is, acts on by permuting the standard basis vectors { e n } n _Е х е Л ig m such that

P( g) en = eg ° n = en' e{ en } neX , where P(g) 's are the operators in Лigm which define the above mentioned linear representation.

Example 3 . Let

X = [0,1,..., m - 1], Gr = Z m = /{0,1,..., m - 1},®\

m

P(0) = "1 1 1 1 , P(1)= " 1 1 1 1 , P(2) = Г 1 [ 1 1 J [ be the cyclic group of order m. Then

1              "		"                          1 "
1		1
	,..., P ( m - 1) =
		1
1		1

In particular, for m =2 and m = 3we have

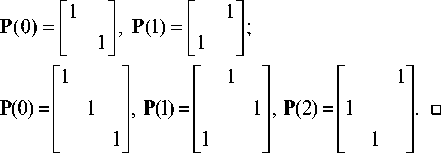
In expression (7) was used linear permutation representation P(g) of only one group . However, we can use others finite groups of given order m. Let Gr = Grm = {g a}m=0 be a group of given order m and {P( g a )}m=1. Then mn-1

Gm+!](Un+1; Grm) = Щ an =0

com ( a n ,0) ( t n |U n +1 ; Gr m ) com ( a n .„ ( t n | U n _{+ 1}; Gr „ )

com ^[ a n , m -1) ( t n \ ^U n +1 ; Gr m )

mⁿ -1

= № an =0

n +1 m

^P m ^{( g} a n ) '

Itn rp 1-mn

T t n

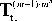
- P m ( g a . )

^com[ n a n - , .0)^{( t} n\ ^U n ; Gr m ) com ( a n _{- 1},1) ( t n I U n ; Gr, )

com ^[ n a n . , . m -1) ( t n \ ^U n ; ^G r m )

is the Golay matrix associated with triple ( Gr m ,{ U m , U m ,..., U m ⁺¹}, Л ig ) .

matrices associated with two triples

Example 4. For m =4 we have two groups: Z 4 = {0, 1, 2, 3} and Z 2 × Z 2 = {(0, 0), (0, 1), (1, 0), (1, 1)}. For both groups we have the following permutation representations:

	" 1			"	1 "		"	1 "		"                  1 "
		1			1			1		1
P (0) =		1	, P (1) =		1	, P (2) =	1		, P (3) =	1
	.	1 J		_ 1	.		-	1 .		-          1 J
	" 1	"		"	1		"	1 "		"                  1 "
		1		1				1		1
P (0,0) =		1	, P (0,1) =		1	, P (1,0) =	1		, P (1,1) =	1
		1 .			1			1          .		- 1               J

Hence, we can construct two different set of Golay

1) ( Z 4 ,{ u m , u m ,..., и m ⁺¹},л ig ) ,

2) (Z2 XZ2,{um,um,...,um+1},лig), respectively.                                             □

Let Qn+i :={Gr™,Gr2,...,Grm,Grm+1}={Qm,Grm+1} be a set   of arbitrary groups   of   given order m —1                             m-1

m : Gr1 = ggM ,...,Gr”+1 = ggI }     . Then we m    l6al fa: =0 , , m       t6™n+1 lan+1 =0

can use on each kthiteration permutation representations {Pm(gak )}m 1 for Grm . In this case, we obtain the following Golay transform mn -1

Gm+PC Un+i;Q„+1) = Щ an =0

com ( a n ,0) ( t n |U „ +1 ; Q n +1 ) com ( a n ,_n ( t n | U „ + i ; Q „ +1 )

^com( a , m —1)^{( t} n | ^U n +1 ; ^Q n +1 )

I t

n

mⁿ -1

= В U an =0

n +1 m

P m ⁺¹ ( g a n ) ■

It is associated with triple

rp 1 mn

T t n

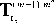
( { Gr m , Gr m ,..., Gr n ⁺¹ } , { u m , u m ,..., и m +1 } , л ig ) .

n +1 m

⁽ g a n )

^com( a n — 1 ,0)^{( t} n | ^U n ; ^Q n ) com ( a n — 1 ,1) ( t n | U n ; Q n )

com ( a n m —1) ( t n |U „ ;Q n )

^com(£ПП) ^{( t} n +1 ) = ^com( a +¹ a n ,a n + 1 ) ^{( t} n , t n +1 ) =

Fast Golay transforms

Let us consider expressions (8) and (9) for m =2 ( i.e., expressions (6) and (7) from our work [7]):

= £( — 1) ^{( a} - ’- )- 'n.,_„( tn + 2 '’■tn „), tn +1 =0                                                  ²

[ n +1]                 l = (-17' n . ^{t n +1 ) a n +} 1тт[ n ]          x

^Co m ( a n — 1 ,a n ,a n + 1 ) ^{( t n} , ^{t n +1} ) ( 1)             com a n — 1 ,a n ® t n + 1 ) ^X

x ( t n ) = ( — 1) ^{a n a} n + ¹ ( — 1) ^a n + ^{1 t n +1} com ( ⁿ I 1 ,a n ® t n+ 1 ) ( t n )

and find matrix representations of these expressions. We introduce the following G -parametrized (2 ⁿ x2 ⁿ )-matrix:

2 ⁿ -1

CT ft [ n ] ,__ I I J p CT

^G 2 n := Г~Т г 2

^a n = 0

c^om[ a n — 1 ,0) ⁽ t n ) ^com ( a n — 1 ,1) ⁽ t n )

2 ⁿ -1

0[ n ]        0

^G 2 n   ПЕ г 2

_n = 0

2 ⁿ -1

1[ n ]         1

^G 2 n      I I Г 2

^a n = ⁰

2 ⁿ -1

G 2 n ^]= Щ ^a n = 0

2 ⁿ -1

¹ G 2 n ^]= В _n = 0

^com ( ⁿ , n — 1 ,0) ^{( t} n ) . ^com ( ⁿ , n — 1 ,1) ^{( t} n ) _ , c^om ( a n — 1 ,0) ^{( t} n ) c^om ( a n —„a^{( t} n ),

ст = 0

<

com i a n — , .0) com^[₍ ^{n ]} ₁₎

c^om ( a n . 1 ,0) com^[₍ ^{n ]} ₁₎

2 ⁿ -1

0 ^G 2 n ^] = В _n =0

2 ⁿ -1

1 G 2 n ^] = В n ⁼0

^{( t} n ), ( t n ) J

^{( t} n )1, ( t n )

ст = 0,

com S a n — 1 ,0) com ^[ ₍ ^{n ]} ₁₎

com ^{[ n ]} ( a n — 1 ,1)

com ^{[ n ]}

( ^a n — 1 ^,0)

. ( t n ) , ( t n ) J ,

^{( t} n ) 1 , ( t n ) ,

G = 0,

G = 1,

and construct the direct sum of introduced matrices

G n ; ^1] = . ^(G) G 2 n ^] = G=0

(0)    [ n ]

2 ⁿ

(1)    [ n ]

2 ⁿ

( I ₂ n — 1 ® P 2 ) G 2 " n ^]

2 n — 1 -1

В 1

n — 1 ⁼0 L

^com( a n — 1 ,0)^{( t} n ) ^com( a n — 1 ,1)^{( t} n )

2 ^{n —1} -1