Маркировка элементов частично маскированных групповых объектов по локальным описаниям ассоциированного сплошного образа

Образы в виде группы точечных объектов (ГТО) представляют собой множества изолированных в пространстве точечных отметок, объединенных групповыми признаками, например, пространственной близостью, контрастом по отношению к фону, устойчивым взаимным расположением и др. [1]. С ними ассоциируют локационные изображения скоплений антропогенных объектов или группы блестящих элементов протяженных объектов [2], астрономические ориентиры [3], множества характерных точек изображений крупноразмерных объектов [4], кластеры данных в признаковом пространстве.

Распознавание групп точечных объектов (ГТО) как человеком, так и техническими системами осложняет несвязность их элементов, узкая автокорреляционная функция их изображений по параметрам геометрических преобразований. Мешающими факторами также служат координатные шумы или флуктуации положений элементов ГТО, фон из ложных отметок, образованный ошибками обнаружения отдельных малоразмерных объектов [5, 6].

Наиболее перспективные подходы к распознаванию изображений данного типа основаны на преобразовании ГТО в связный объект (ассоциированный сплошной образ (АСО)) и анализе его вторичных признаков [1, 5, 6, 7]. Высокой избирательностью обладает признак формы АСО, отображающего конфигурацию взаимного положения элементов ГТО.

Ранее авторами были получены методы формирования АСО и распознавания ГТО, высоко устойчивые к перечисленным мешающим факторам за счет кумулятивного вклада всех элементов ГТО в каждый отсчет описания признака формы [5, 6, 8]. Однако преимущества данных методов оборачиваются их ограничением в предположении, что в поле зрения нахо- дятся все элементы ГТО и он обладает стационарной конфигурацией (существуют постоянные во времени эталонные положения его элементов).

В данной работе проверяется гипотеза о наличии устойчивых признаков формы и у нестационарных, а также частично маскированных ГТО (когда в поле зрения попадают не все его элементы). В качестве таких признаков исследуется ближайшее окружение крайних и внутренних элементов ГТО с цепочечной структурой, а также внешних и внутренних элементов ГТО со структурой скоплений, которые так или иначе составляют ГТО других более сложных конфигураций. В рамках данной работы отнесение элемента ГТО к одному из четырех указанных метаклассов будем называть «маркировкой».

В работе также рассматриваются вопросы использования результатов маркировки для последующего распознавания ГТО.

Постановка задачи

Для целей настоящей статьи примем, что задачи обнаружения отдельных точечных и малоразмерных объектов на фоне крупноразмерных объектов решены [6], решены задачи обнаружения и пространственной локализации групп этих объектов по критерию пространственной компактности [1, 6]. Результаты обнаружения ГТО представлены в виде множества

V = { Vn } = { x n , S n } , n = 1,2,3,..., N , (1)

из N точечных отметок с координатами x n и яркостями s n . Предполагается, что в качестве координат обнаруженных малоразмерных объектов приняты координаты их центров тяжести. Результат обнаружения можно также представить в виде точечной сцены

N

s ( ^X ) = S S n ⁵( x - x n ) , x ^e X , (2) n = 1

где Х – множество допустимых значений координат изображения, 5 ( x ) - символ Кронекера или дельтафункция, в зависимости от дискретного или непрерывного случая соответственно.

На рис. 1 приведен пример точечной сцены с несколькими выделенными пунктиром областями пространственной локализации обнаруженных ГТО. Область № 1 соответствует ГТО с четко выраженной цепочечной структурой, № 3 – типичное скопление, остальные области соответствуют составным (№ 2, 4) и другим более сложным (№ 5) структурам.

Необходимо для каждого элемента vn ГТО найти представление конфигурации его ближайшего окружения (признака формы) zn, а также множество из M эталонных описаний um, m = 1, 2, 3,…, M, которые бы обеспечили достаточно устойчивую в условиях действующих мешающих факторов кластеризацию наблюдаемых реализаций zn в соответствующем признаковом пространстве вокруг M эталонов. Под мешающими факторами подразумеваются: ошибки первого и второго рода при обнаружении точечных и малоразмерных объектов, частичное маскирование ГТО, а также флуктуации координат элементов ГТО, вызванные как координатными шумами, так и нестаци-онарностью их природы.

Рис. 1. Примеры ГТО с различной структурой

В случае стационарных ГТО, примером которых могут служить созвездия небесной сферы, каждый эталон соответствовал бы конкретной звезде из астрономического атласа. В случае нестационарных и частично маскированных ГТО эталон должен быть абстрактным и соответствовать большему разнообразию конфигураций.

По предварительным исследованиям и как можно судить по примерам ГТО на рис. 1, существенно отличаются по своему окружению четыре типа элементов ГТО: 1) концевые элементы цепочки, 2) внутренние элементы цепочки, 3) внешние точки скоплений, 4) внутренние точки скоплений. Их идеализированные описания u m , m = 1, 2, 3, 4, и предполагается использовать в дальнейшем для решения задачи маркировки элементов ГТО.

Формирование локальных описаний конфигурации ближайшего окружения элементов ГТО

Для формирования локальных описаний формы ГТО используем доказавшее свою помехоустойчивость [8] для стационарных ГТО отображение точечной сцены в кумулятивное векторное поле (ассоциированный сплошной образ), но с исключением парциального поля j -го элемента ГТО, для которого формируется это отображение.

N

Zj(x)= X Snh (x - xn) exp (iФn (x)), i = 4-1, h (x) = exp

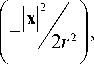
фn (x) = arg(x — xn ) = arctg(Im(x -xn)/Re(x -xn)), где h(x) – функция силы действия парциального абстрактного поля источника, ф(x) - направление действия поля, r – параметр, характеризующий радиус действия парциального поля. Очевидно, распределе- ние потенциала и направления действия такого поля однозначно связаны с конфигурацией расположения точечных отметок.

Для снижения избыточности и инвариантности к смещению и вращениям поставим в соответствие каждому точечному объекту v n локальное описание конфигурации ГТО в виде множества из K отсчетов векторного поля (3), расположенных по окружности радиусом r :

v n ^ z n { z n 0 , z n 1 ,..., z nK - 1 } , ⁿ 1, 2, 3,..., N .

Отсчеты целесообразно брать с равным угловым шагом α с учетом теоремы отсчетов Котельникова.

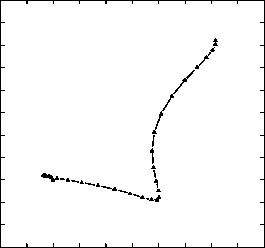
На рис. 2 приведены примеры локальных описаний для двух элементов ГТО: а – совмещает точечную сцену и векторную диаграмму поля в точках взятия отсчетов; б и в – те же отсчеты векторного поля при цепном кодировании на комплексной плоскости.

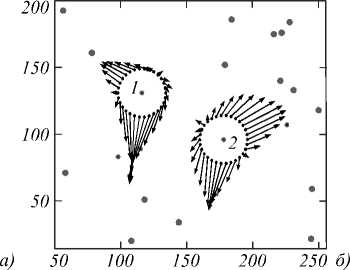
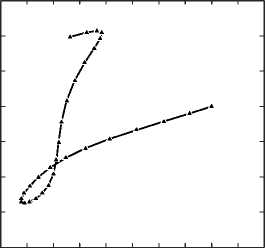
Рис.2. К принципу формирования локальных описаний формы ГТО

Множество таких комплекснозначных отсчетов представляет собой дискретный сигнал или вектор-контур [6] унитарного пространства, к которому применимы известные типовые преобразования и методы обработки [1, 6].

Синтез алгоритма маркировки элементов ГТО

Примем в качестве эталонных идеализированных описаний четырех заявленных метаклассов элементов ГТО соответствующие вектор-контуры точек прямолинейной регулярной цепочки с фиксированным шагом d и регулярного скопления с матричной структурой с таким же расстоянием d между элементами. На рис. 3 показано, что векторная картина поля вокруг заданных типов элементов цепочки сохраняется даже при высокой кривизне траектории цепочки. Эталон- ные описания типовых элементов скопления даны на

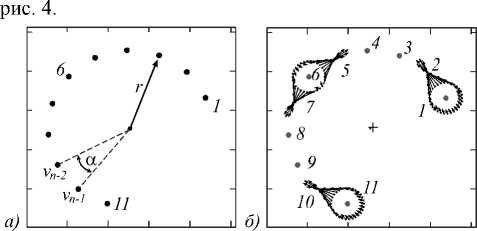
Рис. 3. Характерные описания элементов цепочки

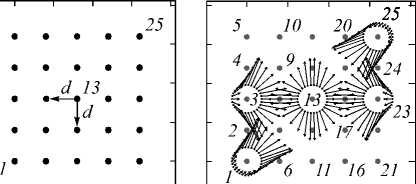
а)                              б)

Рис. 4. Эталонные описания типовых элементов скопления

Локальные описания формы ГТО z n можно рассматривать как векторы или точки в K -мерном признаковом унитарном пространстве C^K . Предполагается, что искаженные указанными ранее мешающими факторами вектор-контуры образуют в этом пространстве кластеры вокруг эталонных центров. При таком допущении в качестве меры схожести вектор-контуров используется расстояние между точками этого пространства, а в качестве критерия распознавания может использоваться минимум расстояния в признаковом пространстве.

Итак, примем, что на этапе обучения для четырех типов элементов ГТО сформированы эталонные век-тор-контуры

{ u m } , m = 1,2,3,4, u m = { u mk } , k = 0,1,2,..., K - 1, (4) а для элементов обнаруженного ГТО множество

{ z n } , n 1, ^2,3,...^, N , z n { z n 0 , z n 2 ,..., z nK - 1 } ⁽⁵⁾ наблюдаемых описаний.

Для удобства дальнейших рассуждений представим все искажения вектор-контуров, вызванные мешающими факторами, аддитивной моделью zn = um (a, Фо ) + gn , (6)

^U m ( a , ^ф 0 ) { u m ( k + a )mod K exp ( i Ф 0 ) } , (7)

где g n — шумовой вектор-контур, Ф 0 - угловое рассогласование эталонного и наблюдаемого изображений ГТО, a – циклический сдвиг начальной точки контура, u m ( a , Ф 0 ) - повернутый и циклически сдвинутый код эталонного вектор-контура.

Тогда оптимальный по критерию минимального расстояния алгоритм маркировки элемента v n ГТО заключается в нахождении в пространстве C^K ближайшего к z n эталонного вектора u m :

H = argmin R (um, Zn), (8) m где R(um, zn) – расстояние между вектор-контурами в признаковом пространстве, Н – результат маркировки, равный номеру самого близкого эталонного век-тор-контура.

В работе [6] показано, что благодаря свойствам скалярного произведения ( u , u (0, ф о )) вектор-контуров в унитарном пространстве C^K перераспределять энергию между своей действительной и мнимой частями

( u , u ( 0, ф о ) ) = cos ф о ||u| |2 + i sin ф о ||u| |2

мешающими факторами. В качестве такой меры искажений для относительности полученных зависимостей использовалась величина – эквивалент отношения сигнал/координатный шум q = d / g . Эти зависимости соответствуют диагональным элементам мат-

и при произвольных масштабах вектор-контуров, участвующих в скалярном произведении, минимальной достаточной статистикой распознавания может служить максимальный (в отношении смещения отсчетов) модуль нормированного скалярного произведения

H

= arg max m , a

|( u m ( a ) , z n )| u m z n

Данный алгоритм оказывается инвариантным к угловому рассогласованию и смещению эталонных и наблюдаемых ГТО, а также к энергиям (нормам) век-тор-контуров.

Важно отметить, что если обнаружение ГТО осуществлялось путем разрушения ребер минимального остовного дерева точечной сцены, в статистическом смысле слишком длинных, чтобы принадлежать ГТО [6], то можно провести для каждого эталона селекцию элементов наблюдаемого ГТО. Так, например, если в минимальном дереве ГТО вершина имеет степень 3, то она может быть отнесена к 4-му метаклассу без вычисления (9) и формирования вектор-контура для данного элемента ГТО. Если степень вершины равна двум, то она не может относиться к 1-му метаклассу, т.е. можно на четверть сократить число проверяемых гипотез в алгоритме (9).

Оценка достоверности маркировки элементов ГТО

Исследование достоверности маркировки элементов ГТО по алгоритму (9) проводилось методом статистических испытаний на компьютерных моделях изображений цепочек и скоплений. В каждом эксперименте генерировался ГТО типа цепочка с заданным относительным (к средней дистанции d между соседними элементами ГТО) радиусом кривизны траектории цепочки R = r / d (рис. 3) или скопление (рис. 4). Флуктуации координат элементов ГТО формировались независимо по центрированному нормальному закону со среднеквадратическим отклонением σ.

В ходе экспериментов заполнялась квадратная матрица частот принимаемых решений P = [ P mn ], где номер строки соответствует номеру метакласса, искаженного эталона на входе алгоритма маркировки, а номер столбца – номеру метакласса, в пользу которого было принято решение.

На рис. 5 приведены характеристики маркировки элементов ГТО в виде зависимостей вероятностей безошибочной маркировки от уровня искажений ГТО

рицы относительных частот принимаемых решений

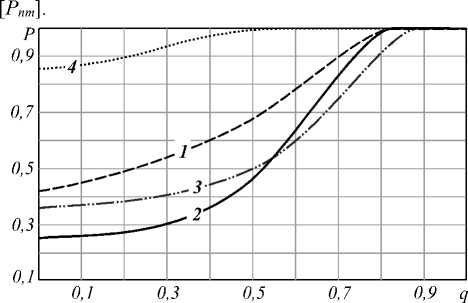
Рис. 5. Зависимости вероятностей правильной маркировки от уровня искажений ГТО мешающими факторами:

• 1    – краевая точка цепочки, 2 – центральная точка цепочки,

• 3 – краевая точка скопления, 4 – центральная точка скопления

Приведем значения других, скрытых в алгоритме (9) параметров экспериментов: относительный радиус парциального поля r 1 = 1,179, размерность вектор-контуров K =60, относительный радиус кривизны траектории цепочки R =5 /3.

Из полученных характеристик следует высокая надежность принимаемых решений вплоть до уровня искажений, когда даже экспертами цепочка воспринимается таковой уже с разбросом мнений. Следует отметить, что мешающие факторы существенно меньше влияют на достоверность правильной маркировки элементов скопления по сравнению со случаем скопления. По мнению авторов, это обусловлено большим кумулятивным вкладом соседних точек из-за большего их числа у любого элемента ГТО типа «скопление».

Заключение

При распознавании групп точечных и малоразмерных объектов и идентификации их элементов в большинстве приложений наиболее информативным признаком выступает форма взаимного расположения точечных объектов группы. Применение известных методов распознавания формы ГТО становится проблематичным, когда в поле зрения наблюдателя попадает лишь часть ГТО одного из известных классов. Существенные флуктуации точечных объектов от своих эталонных положений или отсутствие таких положений у нестационарных групповых объектов дополнительно усложняют решение перечисленных задач.

Использование признаков формы для распознавания частично маскированных и нестационарных ГТО возможно, если использовать не полное, а локальные описания конфигурации соседних элементов ГТО. В качестве локальных описаний предла-

гается использовать дискретизированные цилиндрические сечения абстрактного кумулятивного векторного поля с источниками в элементах ГТО и ограниченным радиусом действия. В качестве устойчивых третичных признаков формы, устойчивых (подобно точкам бифуркаций) в условиях вариабельности и изобилия классов ГТО, предлагается использовать принадлежность каждого элемента ГТО к одному из четырех метаклассов: крайние и внутренние элементы цепочек и скоплений, т.е. результатов четырехвариантной маркировки элементов ГТО.

Инвариантный к смещению, ракурсу наблюдения и норме вектор-контуров из отсчетов указанных цилиндрических сечений векторного поля алгоритм маркировки сводится к определению максимального модуля нормированного скалярного произведения вектор-контура элемента ГТО с четырьмя вектор-контурами метаклассов в унитарном пространстве.

Малое число эталонов в сочетании с невысокой размерностью вектор-контуров, а также инвариантностью к ракурсу наблюдения определяют высокую вычислительную эффективность данного метода маркировки. Дополнительно эффективность может быть повышена предварительной селекцией элементов ГТО и сокращением числа метаклассов по результатам обнаружения ГТО.

Полученные на данном этапе исследований характеристики маркировки подтверждают эффективность рассмотренного метода для нестационарных и частично маскированных ГТО в практически значимом диапазоне уровней вариабельности ГТО.

Результаты маркировки элементов ГТО имеют и самостоятельное значение (подобно идентификации элементов ГТО), но могут также служить основой для дальнейшего распознавания ГТО. В перспективе целесообразно исследовать эти задачи. Например, на поверхности лежит логическая процедура различения ГТО по наличию или отсутствию хотя бы одного из символов алфавита маркировки или использование четырехкомпонентного дискриминационного признака, где каждая из компонент равна числу повторений соответствующего символа маркировки в наблюдаемом ГТО.

Работа выполнена при поддержке грантов РФФИ № 16-01-00451 и Министерства образования и науки РФ №2.3135.2017/4.6.