Master equation averaged over stochastic process realizations for the description of a three-level atom relaxation

Master equations for the density matrix of a quantum dynamical system (QDS) interacting with the environment are widely used in atomic spectroscopy, laser physics, nonlinear optics [1]. For the description of spontaneous relaxation, the environment is modeled by an infinite set of harmonic oscillators in a thermodynamic equilibrium, characterized by the temperature Т [2, 3].

In recent years, a new direction has been intensively developing – the «noisy» optical spectroscopy [4, 5]. The basis of this direction is the study of a QDS response on an external stochastic field. The study of related issues is actual today because of the experiments in the spectroscopy of isolated molecules [6] and development of quantum information and quantum computing theories [7–9].

In [10], the nonequilibrium density matrix method is used for studying relaxation of a QDS interacting with a heat bath and an external stochastic field. The balanced type master equations describing levels population evolution were obtained, and the probabilities of transitions in a three-level QDS are calculated. In [11, 12], the radiation line shape is calculated for a two-level system interacting with dichotomous noise.

In [13], the master equation was reduced to a Fokker-Planck equation by the method of generalized coherent states. The solution of the Fokker-Planck equation is used for calculation of the probability for the atom to be in an excited state and shapes of radiation lines in presence of a delta-correlated process. Relaxation of a three-level atom in a heat bath and an external stochastic field is investigated in [14] for a delta-correlated process and a Kubo-Anderson process. Radiation line shapes are obtained in the explicit form, and the influence of adjacent transitions is showed. In [15], the dependence of a solution of the Fokker-Planck equation describing relaxation of a two-level atom in a stochastic field on the order in which the averaging over realizations of the stochastic field is applied to the QDS is investigated.

The present paper goal is to obtain the master equation averaged over stochastic field realizations, to calculate radiation lines shapes employing it, and to compare the shapes with the ones obtained in [14] by perturbation theory.

1.    Problem formulation

In this paper we consider relaxation of a stationary three-level atom interacting with a photon heat bath and an external stochastic field. We propose a new approach that allows investigation of the interaction of the atom with the stochastic field in the same order of perturbations theory as used for the interaction with the photon heat bath.

The model Hamiltonian of a quantum system consisting of a three-level atom, a photon heat bath, and a stochastic field is given by

Л      Л        Л        ЛЛ

H = Ha + Ht + Hat + Ht,(1)

where HA is the Hamiltonian of the three-level atom

TH A = Am H1 + М2 H2,(2)

HT is the Hamiltonian of the photon heat bath, which is modeled by an infinite set of harmonic oscillators,

^

Ht = £ AmM ,(3)

k = 1

HAT is the Hamiltonian of interaction between the atom and the heat bath, written in the rotating wave approximation,

^

H AT = * 3 ( / 1 J + + f 2 k K + + f 3 Л) b k + h . c . | ,     (4)

k =1 ^{L                                           J}

Hst is the Hamiltonian of interaction between the atom and the stochastic field

H_st = й ( Q ( t ) H 1 +S ( t ) H 2 ) +

+ Й ( ^ ( t ) J ₊ + Z ( t ) K T ₊ + % ( t ) L ₊ + h . c . ) .

Here, ω k is the frequency of the k -th mode of the heat bath field; b k and b k ⁺ are creation and annihilation operators of the k -th mode of the heat bath; f 1k , f 2k and f 3k are constants of the atom-field interaction with the k -th mode of the heat bath; Hi and H2 are the diagonal operators defining energy levels of the atom; J± , KC ± and L, ± are transition operators between atomic energy levels (Fig. 1); Ω( t ) and Ξ( t ) define random shifts of atomic energy levels; ξ( t ), ζ( t ), and λ( t ) are random functions, proportional to the stochastic field intensity and defining transitions between atomic energy levels. The stochastic processes described by the random functions Ω( t ), Ξ( t ), ξ( t ), ζ( t ), and λ( t ) are assumed to be ergodic.

In the interaction picture by the atomic subsystem and the heat bath, the interaction energy operator is given by

( Hl, + TT, ) t                                  - ( Hi. + TT, ) t

V ( t ) = e ^{й (} A T ) ( H AT + H st ) e ^{й (} A T ) = V AT ( t ) + V_S1 ( t ) (6)

where

и

Vat (t) = *Z k=1

+ f 2 k K + e

I

+ f 3 Лe^{( a} 0 ^{+Ю 0} -“ ^k ) b^ + hC .

V t ( t ) = Й ( Q ( t ) H 1

( i

+ B ( t ) H ) + Й ^ ( t ) e

и In „+^0 I „

■ ^{1     2 J} J ₊ +

и ^Ю 0

+ Z ( t ) e ² K ₊ + X ( t ) e ^{( n} ° ⁺™ ⁰ ) L ₊ + h . c .

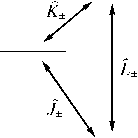
e>o/2

do-\-too/2

Fig. 1. Notation of the three-level atom transition operators

Interaction between the atom, the heat bath, and the stochastic field is described by the Liouville-von Neumann equation [1,16]:

i Й ( др ат / д t ) = [ V ( t ) , p ат ] .                             (9)

A formal integration of (9) gives

t

P aT ( t ) = P aT ( 1 0 ) - ( i /^)\[ V ( t ' ) , P ат ( t ' ) ] d t '.       (10)

t ₀

Substituting (10) in (9), we obtain

^{( др} aT ( t ) ^{/ д} t ) = ^{- (} i ^{/ Й ) [ V} ( t ) , ^P aT ( t 0 ) ] ⁺

+ ( - i / Й ) ² J [ V ( t ) , [ V ( t ' ) , p aT ( t ' ) ]] d t '. t ₀

Using the irreversibility approximation and the second order of perturbation theory for the small interaction V ( t ), the equation (11) can be written for the reduced density operator

P ( t P a ( t ) = Tr_T [ P aT ]                                (12)

in the following form

( д р/ д t ) = ( Y 1 /2) [ ( N 1 + 1 ) ( 2 J - P J - J J - P - P J J . ) +

2 J + P J _ - J - J ₊P-P J - J + ) ] + ( у 2 /2) x

( N ₂ + 1 ) ( 2 K _ P K ₊ - K ₊ K _ P - P K ₊ K - ) +

2 K + P K - - K - K + P-P K - K + ) ] + ( Y 3 /2) x       (13)

( N 3 + 1 ) ( 2 L - P L + - L + L - P -P L + L - ) +

+ N 3 ( 2 L + P L- - L - L+P - P L - L + ) ] - ( i / Й ) [ V^t, ( t ) ,p ( 1 0 ) ] +

(-i/Й)2 J[Vpst (t),[V^st (t'),p(t)]]dt', t0

where γ 1 , γ 2 , and γ 3 are damping constants of the atomic subsystem

Y1 = 2n| f y|2 g (Юу)! %.=П0+(Ш0/2),

Y2 = 2n| f2у|2 g (ЮУ)| my=(m0/2),

Y3 = 2n|f3y|2 g(Юу-)| ™У=П0 +ю0 .

Here, g (ω ) is the density of states in the heat bath; N 1 , N 2 , and N 3 are average numbers of photons in the heat bath on the transitions 2 → 1, 3 → 2, and 3 → 1 respectively:

N1 = [exp(Й(2Q0 irn )/2kT)-1]-1,(17)

N2 = [exp(ЙЮ0 /2kT)-1] ,(18)

N3 = [exp (Й (Q0 + ®0) / kT)-1] .(19)

Averaging Eq. (13) over realizations of the stochastic field, one can obtain d

/dt = Ko(TH1 (p) 7H1 - TH2 (p)) +

+ K _s(T H 2 (P) T H 2 - T H ² (P)) +

+ ( П 1 + K , )(. 7 -^ .^p + - .7 + . 7 -( P) ) +

+ ( 8 1 + K , ) ( J+(P) .J - - .J - . J +( P) ) +

+ ( П 2 + K _с ) ( KK -( P) K + - KK + K -( P) ) + + ( 8 2 + k z ) ( K +( P) K - - K - K +( P) ) + + ( П 3 + K _x ) ( L-( P L L + - L L + L-( P ) + + ( 8 3 + K _x ) ( L L +( P) L L - - L L - L L +( P )) + + h . c .,

where

П у = ( Y y /2) ( N y + 1 ) , 8 y = ( Y y /2) N y , у = 1,2,3 ;(21)

K _й

J (Q( t ) Q ( t 1 )) d t 1 , t ₀

t

K= = J (5( t )5(t1)}d t1, t0

t

K , = J ^( t ) ^ ( t 1 )) d t 1 , t ₀

t

K y = J (X( t ) % ( t 1 )) d t 1 .

t ₀

t

K ^ = J (?( t ) Z ( t 1 ))d t 1 , (22)

t ₀

In derivation of Eq. (20) we assumed that average values of all random functions and the two-point correlation functions not presented in (22) are equal to zero. We also discarded terms of higher degree of smallness in respect to V ( t ), which appear when expending average values of expressions that contain a product of a random function and the density matrix operator ρ̂.

2.    Solution method

In the matrix representation, Eq. (20) takes the form of a system of ordinary differential equations for ele-

ments of the density matrix < ρ̂ ( t )>. Matrix realization of

the operators J +, Kt +, L, +, H 1 , and H 2 can be selected to be

the following:

( 0 0 0 )        ( 0 1 0 )

./ + = 0 0 1, K f + = 0 0 0,

ч 0 0 0 J       ( 0 0 0 ?

' 0 0 1 A        ( 10 0 ^

L + = 0 0 0 , H 1 = - 0 0 0 ,            (23)

ч 0 0 0 J        2 ^ 0 0 - 1 ?

f 1 0 0 A

H f2 = 10 1 0 .

2 3

( 0 0 - 2 J

The two-point correlation function of a creation operator  + and an annihilation operator  - can be calculated by a shift of the initial conditions for the atomic subsystem density matrix [17]:

/x A ₊ ( 0 )x A ( t)\ = h^e_e-i ^m- t|

\ +v - \ I         ^ j/            lp ( 0 ) ^p ( 0 ) .^+ ( 0 )

.

For example, the correlation function of operators J + and J — can be written

(./ + ( 0 ). / - ( t )) =

^- i ™ 12 t ^- J ( § 2 ⁺¹ Ъ ⁺Л 2 ⁺ⁿ 3 ⁺ K Z ^{+ 2} K z ⁺ K X ⁺ 4 K й )^d t 1

= P 22 ⁽ t 0 ) ^e      0

Substitution of (23) in (20) gives

(Р_п) = - 2 ( ^ +П з ⁺ K z ⁺ K X )< Р 11) ^{+ 2} ( § 2 ⁺

⁺ K z ) (^р22 ) ^{+ 2} ( § 3 ⁺ K X )( Р з3 ),

(Р 12 ) = ^- ( § 2 ^{+ П} 1 ^{+ П} 2 ^{+ П} 3 ⁺ K Z ^{+ 2} K z ^{+ K} X ⁺ + (1/4) K й )< р ₁₂>,

(Р 13 ) = ^- ( § 1 ⁺ § 3 ^+п 2 ^+П 3 ⁺ K Z ⁺ K z ^{+ 2} K X ⁺

⁺ K й ⁺ K S ) (Р 1з) ,

Other correlation functions have similar form.

In the case when the stochastic field is given by a delta-correlated process, the integrals of correlation functions (22) become

t кa= J 2(^a/va )§( t -11) d t1 = (aa/va),            (36)

t ₀

where α = ξ, ζ, λ, Ω, and Ξ; σ α ² are the variances of corresponding random processes; ν α are frequencies of external influences on the considered system.

Finally, the radiation lines shapes have Lorentzian form:

^r i

(^Р 21) = ^- ( § 2 ^+п 1 ⁺ⁿ 2 ⁺ⁿ 3 ⁺ K Z ^{+ 2} K Z ⁺ K X ⁺

+ (1/4) K _й )( р ₂1) ,

(Р 22) = ² ( ^П 2 ⁺ K Z )( Р 11) ^{- 2} ( § 2 ^{+ П} 1 ⁺ K Z ⁺

^{+ K} Z ) (^р22 } ^{+ 2} ( § 1 ⁺ K Z )( Р зз) ,

(Р 23 ) = ^- ( § 1 ⁺ § 2 ⁺ § 3 ^+П 1 ^{+ 2} K Z ⁺ K Z ⁺

+ K х + (1/4) K й + K _а )( р 2з) ,

(^р 31) = ^- ( § 1 ⁺ § з ^+п 2 ^+П 3 ⁺ K z ⁺ K z ^{+ 2} K X ⁺

⁺ K й ⁺ K = )(Р з1) ,

(^р 32) = ^- ( § 1 ⁺ § 2 ⁺ § з ^+П 1 ^{+ 2} K Z ⁺ K z ⁺

+ K х + (1/4) K й + K _а )( р з2> ,

(^р33 ) = ² ( ^П 3 ⁺ K х )Ф 11) ^{+ 2} ( ^П 1 ⁺ K Z ) (^р22 ) ^-

^- 2 ( § 1 ⁺ § 3 ⁺ K Z ⁺ K X ) (Р зз )•

g j ⁽™^{) = 1} 2 / Y ^ПГ j I ( ™ ™ у )

2 ,

0 2   0 2   0 2

Г ₁₂ = § 1 +§ ₂ + § ₃ +П 1 + 2— + — + — +

+ 1 ° « +° ^ , 4 V й   v_H

VZ   vz

VX

_                     °E  , Oz

Г 23 = § 2 + П 1 + П 2 + П з ++ 2 —

VZ     vz

1 ^CT 2

+7 , 4 V й

+ —+

VX

3. Calculation of radiation line shapes

By definition, the radiation line shape of an atom on the transition i → j is calculated as

от gj (to) = Re Je™' A( 0) A-( t)) dt,                  (33)

where by the angle brackets a two-point correlation function is denoted;  + and  - are transition operators between the levels i and j .

О О            О   ^O z     0 2

Г 13 = § 1 + § 3 + П 2 + П з +++ 2 + ^vZ ^vz ^vX

+ —+ ^, vй  v=

Ц2 =Й 0 + ( Ш ₀/2), « 23 = ( « 0 /2), ® 13 =Й 0 +® 0 .(41)

To obtain radiation lines shapes of the atoms with one of its transitions forbidden by the optical selection rules it is necessary to set in Eq. (38) - (40) equal to zero the constants of the forbidden transition. Further, everywhere, when considering atomic configurations, for a V -atom the constants δ 2 , η 2 , and σ ζ have to be taken equal to zero, for a Ξ-atom – the constants δ 3 , η 3 , and σ λ , for a Λ-atom – the constants δ 1 , η 1 , and σ ξ .

In [14] we obtained radiation line shapes for a three-level atom interacting with a heat bath and a weak stochastic field. We used perturbation theory to consider the

impact of the interaction between the atom and the stochastic field. Analysis shows that the radiation lines shapes in [14] equal to the first two terms in the expansion series of (37) by the stochastic field intensity.

Fig. 2 a and b illustrate the differences between the shapes of the radiation line of a V -atom on the transition 2 → 1 obtained by perturbation theory in [14] and by Eq. (37). The following values of parameters are used: Ω 0 /ω 0 = 2, δ 1 /ω 0 = 0.5, δ 2 /ω 0 = 0, δ 3 /ω 0 = 0.5, η 1 /ω 0 = 0.5, η 2 /ω 0 = 0, η 3 /ω 0 = 0.5, σ Ω /ω 0 = 0.1, σ Ξ /ω 0 = 0.1, ω 0 /ν Ω = 1, ω 0 /ν Ξ = 1, ω 0 /ν ξ = 0.7, ω 0 /ν ζ =0, ω 0 /ν λ = 0.7, σ ζ /ω 0 = 0. The stochastic field intensity is varied by parameters σ ξ and σ λ .

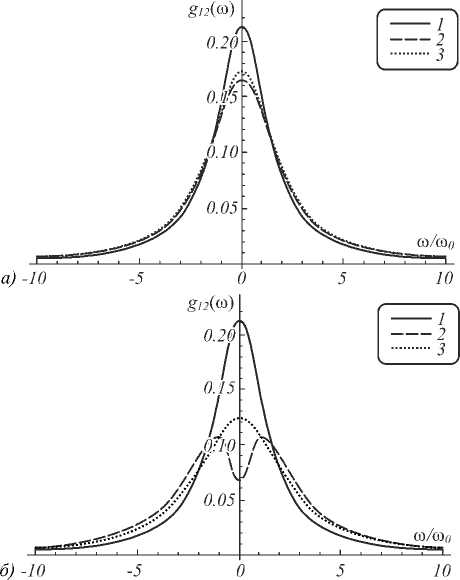
Fig. 2. Shapes of the radiation line of a V-atom on the transition

2 → 1 for the values of the delta-correlated process intensity: σ ξ /ω 0 = 0.4 and σ λ /ω 0 = 0.4 (a), σ ξ /ω 0 = 0.7 and σ λ /ω 0 = 0.7 (b). The line 1 denotes the radiation line shape when the field is absent, the line 2 – the radiation line shape obtained by perturbation theory in [14], the line 3 – the radiation line shape given by (37)

In the case when the stochastic field can be represented by a Kubo-Anderson process, Eq. (22) takes the form t

K α = ∫ σ ² α e ^{-να ( t - t 1 )} d t 1 ,                                     (42)

t ₀

where notation (41) is used.

When the frequencies of collisions are sufficiently high, i.e. max (σ α ² / ν α ²) << 1 and ( ω 0 + Ω 0 ) / max (ν α ) << 1, contours of the radiation lines are Lorentzian

g ij ( ω ) = (1/ π )( Γ ij /[ Γ i ² j + ( ω- ( ω ij +∆ω ij ) ) ² ]), (43) where Γ ij are given by the same expressions as in the case of a delta-correlated process (38) – (40), ω ij are defined by (41), Δω ij represents a shift of the central peak

σξ2       σζ2

∆ω12 = 2ω12 2ξ -ω23 2ζ + ω13 λ ,(44)

12        12 ν 2 _ξ 23 ν_ζ 2      13 ν 2 _λ

^∆ ω 23 ⁼

-

σ_ζ 2

23    + ω13

23 νζ213 2

^σξ ² ω 12   ^ξ + 2 ω

12 ν_ξ 2

ν

λ

^∆ ω 13 ⁼

σξ      σζ

ω12    + ω23    + 2ω13

νξ2        νζ2         ν 2λ

where notation (41) for the transition frequencies is used.

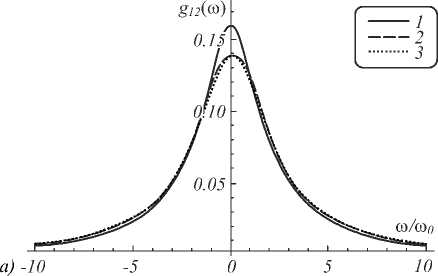
In Fig. 3 a and b , we show the differences between the shapes of the radiation line of a V -atom on the transition 2→1 given by Eq. (43) and obtained in [14]. Here, the following values of parameters are used Ω 0 /ω 0 = 2, δ 1 /ω 0 = 0.5, δ 2 /ω 0 = 0, δ 3 /ω 0 = 0.5, η 1 /ω 0 = 0.5, η 2 /ω 0 = 0, η 3 /ω 0 = 0.5, σ Ω /ω 0 = 0.1, σ Ξ /ω 0 = 0.1, ω 0 /ν Ω = 0.1, ω 0 /ν Ξ = 0.1, ω 0 /ν ξ = 0.1, ω 0 /ν ζ = 0, ω 0 /ν λ = 0.1, σ ζ /ω 0 = 0. Parameters σ ξ and σ λ specify the intensity of the stochastic field.

gi?*®)

0.15 h

б) -10

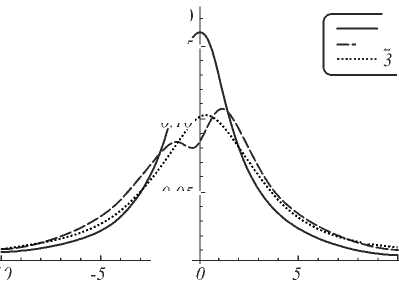
--2

0.05 H co/coo

Fig. 3. Shapes of the radiation line of a V-atom on the transition 2 → 1 for the values of the Kubo-Anderson process intensity: σ ξ /ω 0 = 2 and σ λ /ω 0 = 2 (a), σ ξ /ω 0 = 1 and σ λ /ω 0 = 1 (b). The line 1 denotes the radiation line shape when the field is absent, the line 2 – the radiation line shape obtained by perturbation theory in [14], the line 3 – the radiation line shape given by (43)

O'. 10'

The proposed method of averaging of specific realizations of the random processes Ω( t ), Ξ( t ), ξ( t ), ζ( t ), and λ( t ) leads to a zero contribution from the first term in the right part of (11) into the final expression for the master equation (20), which describes only relaxation processes in the considered case. The external stochastic field acts like a heat bath, which is reflected in Eq. (20). Here, the constants describing the photon heat bath and the correlation functions of the stochastic fields are included in the same way.

This leads to the situation when the equations for the diagonal density matrix elements (24), (28), (32) form a closed system, and the equations for the non-diagonal elements are decoupled. As a result, the radiation lines shapes for a delta-correlated process (37) and a Kubo-Anderson process (43) are Lorentzian.

The finiteness of the correlation time for a Kubo-Anderson process lead to a shift of the center of a radiation line shape by Δω ij , which is dependent on the resonance frequencies of atomic transitions and parameters of the stochastic field. Numeric modeling of the obtained results for radiation line shapes and comparing them with the results from [14], derived with help of perturbation theory, show that the radiation line shapes are in good agreement in the area of validity of the perturbation theory. Increasing of the stochastic fields intensity lead to growing difference between the Lo-rentzian line shapes (37) and (43) and the radiation line shapes from [14], the emergence of a valley (Fig. 2 b ) and significant deformation (Fig. 3 b ).

Conclusion

In the present paper, the efficiency of the method of averaging over stochastic fields realizations at the stage of deriving of the master equation is showed. The method is used for describing relaxation of a QDS interacting with a photon heat bath and an external stochastic field, which can model the stochastic character of the dipoledipole interaction between the QDS and the environment or a fluctuating component of the broadband laser radiation. The exact solutions are obtained. A delta-correlated process and a Kubo-Anderson process are examined. Explicit expressions for radiation lines shapes, containing parameters of the stochastic processes, are derived. It is showed that the radiation lines shapes are Lorentzian. For the Kubo-Anderson process an explicit expression for a shift of the center of the Lorentzian contour is obtained. The presented approach allows to define the times of longitudinal ( T 1 ) and transverse ( T 2 ) relaxation of a three-level atom in a stochastic field and also to find the relationship between T 1 and T 2 . It will be the subject of our further research.