Математическая формализация алгоритма демодуляции по правилу максимума апостериорной вероятности, минимизирующего вероятность ошибки на символ

Алгоритм Витерби (АВ), рассмотренный в [1-2], минимизирует вероятность ошибки на блок информационных символов, в котором производится поиск кратчайшей траектории на решетке дискретных альтернатив. Алгоритм Кловского-Николаева (АКН) минимизирует вероятность ошибки на бит при минимально возможной задержке принятия решения.

Оба алгоритма работают с текущим потоком данных и в рамках своих возможностей непосредственно выдают решения или группу решений. АКН выдает решения на каждом тактовом интервале. При этом задержка принятия решения постоянна и равна максимально возможной величине памяти канала. АВ в условиях оптимальной работы решение выдает по мере того, как происходит схождение траекторий по решетке Витерби. Это означает, что задержка в принятии решения может быть произвольной величиной, но так же, как и у АКН, не меньше величины, соответствующей памяти канала. В [1] приведена формула, по которой можно определять задержку принятия решения для АВ. Фиксация задержки принятия решения в АВ позволяет получить субоптимальный алгоритм, который удобен в практической реализации.

Алгоритм максимума апостериорной вероятности (МАВ), в отличие от рассмотренных выше, работает с блоком информационных символов , который должен быть окружен (в начале и конце) известными информационными символами. При описании алгоритма МАВ [3] такими символами обычно являются «нулевые» из двоичного алфавита. В данной статье МАВ рассмотрен для любой возможной позицион- ности символов, а также для ситуаций, когда анализируемый блок окружают как известные символы, так и неизвестные символы соседних блоков. Такая задача рассматривается в рамках блочного моделирования радиотехнических устройств [3], позволяя универсально использовать алгоритм МАВ , например в задачах демодуляции сигналов .

Постановка задачи

Для анализа алгоритма применим теорию дискретного марковского процесса.

Пусть процесс протекает в дискретном времени с постоянным шагом. Для моделирования канала с памятью воспользуемся сдвигающим регистром с длиной (первая ячейка регистра содержит текущий информационный символ), на вход которого поступают информационные символы блока некоторой детерминированной функции и на выходе функции добавим идеальный канал без памяти с белым гауссовским шумом (рис. 1).

В условиях МСИ параметр Q обозначает относительную память канала [1; 4]. Значения элементов входной последовательности b^VA-A-J выбираются независимо согласно некоторому распределению вероятностей, и каждый элемент может принимать одно из m значений на входе модулятора.

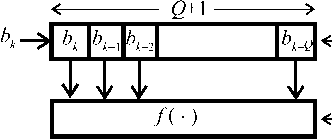
Сдвигающий регистр с иг' комбинациями

Детерминированная функция

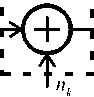
Идеальный канал без памяти с белым гауссовским шумом

Рис. 1. Упрощенная модель канала с памятью в дискретном времени на основе регистра сдвига

При этом обязательно выполняется равенство УЖ =0=1. На выходе блока детерминированной функции (1) каждый элемент последовательности У к определяется новым входным значением bj, , поступившим во входную ячейку сдвигающего регистра, и значениями в других ячейках сдвигового регистра ^-1 ’ ^А-2 ’ •■•’ ^А—О ’ которые были перезаписаны туда после операции сдвига. Каждый элемент наблюдаемой последовательности на выходе канала 2 к = Ук+^_к, где ^к – отсчеты белого гауссовского шума. Таким образом, рассматривается m -ичный марковский процесс v -го порядка.

Для предложенной модели со сдвиговым регистром введены [2] определения состояния х_кЦь_к__А,Ь_к-1>-Л-д) и перехода ^Дь_к1ь_к-г-Л-о\ Состояния образуют пространство X . Число состояний в этом пространстве |х| = т®. Переходы образуют множество с числом элементов |е| = т .

Для модели, показанной на рис. 1, введено [1] определение комбинации

Кк "Ук-д , Ьк_д+\ , Ьк_А , Ьк )

Комбинация полностью определяет переход. Будем считать, что дискретное время k может принимать как положительные, так и отрицательные значения. В интервале 1<к<В производится передача блока информационных символов ^к } . Вне этого интервала могут передаваться как известные, так и неизвестные символы.

Известные символы могут быть произвольными из используемого алфавита размером m и принимать значения от 0 до т -1 . Кроме того, алфавит дополнен еще одним символом с номером m. Это дополнение означает, что каждая ячейка регистра сдвига характеризуется m +1 состоянием. Символ с номером m означает начальное «пустое» состояние, соответствующее «физическому нулю» для сигнала.

Неизвестные символы могут быть информационными и принадлежать другому информационному блоку. Неизвестные символы, находящиеся вне диапазона 1<к<В, не входят в задачу определения их информационного содержания. Число элементов последовательности z составит B + Q, то есть

7, yZy, Z2, ..., Z к ,

•"’ ZB+Q-l ’ “В+О

Таким образом, постановка задачи заключается в следующем: имеется последовательность Z наблюдений дискретного по времени марковского процесса с конечным числом состояний |х| = т (или комбинаций |K| = m0+1, Q – память канала; m – позиционность символов ^к ), наблюдаемого на выходе идеального канала с белым гауссовским шумом. В каждый k-ый момент времени требуется найти наиболее вероятный элемент Ьк входной последовательности b = (b0,bv...,bk,...,bK_A\ для которого апостериорная вероятность Pw) максимальна, что соответствует критерию МАВ.

Описание алгоритма

Символ b^ представлен как переменная, принимающая значения bk = z" = 0, m -1 . Тогда и условную плотность вероятности (ПВ) X'(i|6.) для каждого символа ^A можно представить как Hzjbk = z). В сдвигающем регистре (см. рис. 1) входные символы ^k заходят слева направо. Мысленно развернем регистр так, чтобы данные в него заходили справа налево. Тогда состояния в момент времени k обозначим как

Xk.j ~ ^k-Q ’ ^A-0+1 ’    ^A-2 ’ Ьк_х ) = j , где j = 0, me -1 – порядковый номер состояния, совпадающий с числом в m-ичной системе счисления, образованным содержимым в таком сдвигающем регистре при условии, что рассматриваются только Q последних ячеек.

При решении поставленной задачи для заданной последовательности наблюдений z любому символу Ь _k ставят в соответствие величину (метрику), пропорциональную -^P(b_k,i), где p^.i} – совместная вероятность того, что символ b_k примет заданное значение, а сигнал z , как точка в многомерном пространстве сигналов, попадет внутрь некоторого элементарного объема S-Y

"^dz, , часто обозначаемого [4-5] как di .

i=0

Учитывая, что

P(bk, z e di) = W(z)P^bk \i)di , то поиск максимума P\bk, z) соответствует поиску максимума H^|4 что дает в итоге решение поставленной задачи максимизации H6^) для поиска наиболее вероятного символа ^k " Здесь ^(z) – многомерная ПВ распределения последовательности сигналов, объединенных в вектор z.

Используя байесовский подход, можно перейти к другим вероятностям

P^b_k , z e di) = P^b_k |z) W^i)di = ^(г|/>₄ )Р(Д )di .

Здесь И%) – ПВ распределения i при условии передачи символа ь_к. НьД^) – апостериорная вероятность передачи символа bk • Отсюда

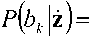
И#. H.) ^(z)

и максимум апостериорной вероятности ml 4 соответствует максимуму произведения ^ыт.) .

Наиболее вероятный символ Ьк следует искать исходя из введенных понятий состояния и перехода. Переход ^ к из состояния ^Xk ^{B X}J-+1 связывает два момента времени к и к +1

^=k-+i,^-)=k -^^+i и предполагает появление во входной ячейке сдвигового регистра символа bk+\ .

Совокупность состояния (или последовательности символов) *^'/,' + 1 и символа bk+\ образует комбинацию ^ kp\ в сдвиговом регистре, из которой формируется сигнал Уа+1 и в конечном итоге сигнал на выходе канала ^A+l " Аналогично, совокупность состояния X и символа ^ к образует комбинацию ^Kk ’ что в итоге формирует сигнал z . Однако в комбинацию ^Kfc входит последовательность x_k+x . Обозначим ее как ^X'k =^Xk₊V

Таким образом, последовательность ^ к имеет место при формировании сигналов ^Zk ^{И Z}k+Y и содержит передаваемый искомый символ bk . В этом случае можно ввести пятимерную (при рассмотрении квадратурных компонент сигнала) совместную ПВ M^zk^k₊nb_k), которую можно связать с пятимерной ПВ M^zk ’ > ^Xk ) как

w(zk,zk+x,bk)= ^lV^k,zk+x,xk)

ПриэтомПВ ^(Zk,2_k+x,X_k)=P7(z_k,Z_k+x,X_k+1) можно представить состоящей из ПВ K^zk ^'^ H^zk, ^хы ) и w^_k+x, x'_k) = w(z_k+x , x_i+1).

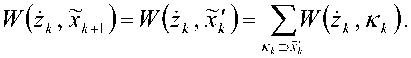
В формировании сигнала ^/c + l участвует комбинация ^Kk+\ ^— (^XA+1 ’ Ь_к+\ )— \b_k_Q₊Y , - .., Ь_к+Х ). Совместная ПВ распределения сигнала ^ kp\ и наличия в сдвиговом регистре той же самой последовательности ^Xk₊Y =^b_k__Q+Y,...,b_k)

H^Zk₊Y’^X_t+1)= ЕН^₊1^А₊1)-   (4)

В выражении (3) ПВ H^l^) соответствует произведению ПВ распределения сигнала 2" при условии передачи символа bk и нахождении системы со сдвиговым регистром в состоянии к ? на вероятность передачи этого символа и на ве- роятность нахождения этой системы в состоянии

W_k ^^ ^w^k к, b_k )p(x_k )p(b_k ). (5)

Аналогично в выражении (4) для ПВ имеет место

В выражении (10) каждое слагаемое суммы содержит состояние ^Xk -^vt+l . Это состояние в своей последовательности содержит всегда один и тот же искомый символ bk . То есть каждое слагаемое умножается на одну и ту же вероятность p(b_k ) . Вынесем эту вероятность за знак суммы.

W(zk+A,KkM =

= ^k₊i k/_c+i, ь_к+1 )p(x_k+2 )р(ь_к+А )= (6)

= ^k₊i k/_c+i, ь_к+1 )pK’₊₁ )p(b_k+l).

^(zfc,zk+A,xk+A) =

= K^b к ) E ^W^k Vk ^ b_k )P_a К к) ^x

Kk ^x’k

x E^fe+il^i’^iKfcM^i)

Вероятность нахождения системы в соответ- ствующем состоянии будет определяться соот- ветствующей нормировкой ПВ, чтобы выполнялось условие У^,)=1:

hs.,^ л+)

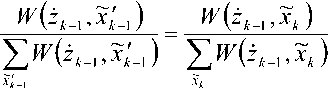
— (8)

Выражение (7) показывает, что И^Л₊1) в (3) определяется в итоге через H^-i,^J, а выражение (8) показывает, что ^(z_k+1,x_k+1) в (4) определяется через ^(^Zk+2’^Xk+2)‘ Это означает, что H^Mj будет определяться по цепочке очередными предыдущими во времени выражениями, а W(z_t+A,x_k+A) – выражениями, которые следуют по времени позже. Обозначим все зависимости, уходящие в прошлое, значком a , а уходящие в будущее – P . В силу независимости отсчетов шума и с учетом новых обозначений можно записать

H^Zk , ^zw > ^₊i) = ^« M, ^) M k+i, ^-₊i), (9)

что соответствует предположению о факторизации ПВ K^W_wY

Параметры а и p в (9) соответствуют функциям вероятности, обозначенным также в [3]. Подставляя (3)-(6) в (9), получим

W(zk,zfc+A,xtM =

= У^_а (z_k ,K_k\ Y W „ (z^, K_k+A ) =

= ^JP^z_k Jx^, b_k ^jP_a (x_k }P(b_k ) x        (10)

x E^fe+ik+i’^ifefe^M^i).

Тогда с учетом (2)

Mzk^k+1,bk)=

=p№

£ K^zw |^₊1 ’ ^bW И k₊2 Mb to ) ’

В выражении (12) вероятность ^PaKK вычисляется по цепочке, уходя в прошлое до момента времени к — 1 . В момент времени к — О определяются вероятности начальных состояний до начала блока элементов последовательности z . Вероятность к (^Xt+2 ) также вычисляется по цепочке, уходя в будущее до момента времени . В момент времени к = В + Q + 1 также будут определены вероятности начальных состояний после этого блока.

Формула ПВ (12) будет определять достаточную статистику для использования ее в решении задачи максимизации произведения wtoMa . Из (12) можно заметить, что множитель справа от р^к ) как раз и представляет собой ПВ И%)’ где в сумме имеются составляющие, рекуррентно связанные между собой на всем протяжении блока элементов последовательности Z.

Найдем все эти рекуррентные зависимости с учетом того, что комбинации и состояния образуют числа в m -ичной системе счисления:

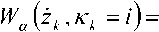
= W z,x

— ,b_k =imodm х т *

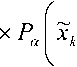
P(bk =imodm\

i = О, me+1 -1, i = 0, m -+1 -1,

^z (z_k ,x_i+1 = i)=A ^k A=^ =     (14)

^ ^wa h ,K_k=i-m^Q+ j), i = 0, m ⁹- 1,

/=0

^Pa^k^=^Pa^'k =0 =

= У^а^^к’^х'-^ ,i = w 1, (15)

У^ЛчА =A bk = arg max W(zk, zk+1, bk = z), z = 0, m -1, к = 1, В,

так и «мягкого» решения, которое используется при декодировании помехоустойчивых кодов. Такое «мягкое» решение может быть определено как вероятность

P{b_k^i^ ^k^A-i") ^^"_X(22)

УА^к’АхЛ =y)

7=0

W_p(z_k,K_k = z)

= W z

k

- A m

= z mod in x

x Pp \x_k = i mod m ⁹ )P(b_k = i mod m\

На рис. 2 схематически показаны две соседние комбинации ^Kk ^{И K}W а также состояние, которое содержит последовательность символов, входящую в обе комбинации ^k = ^-₊1 . В этой последовательности имеется символ b_k , в пользу которого будет принято решение.

Мж' -1,

WP ^k Ak=^^ Wp (zk ,кк=Ьт+ j\

_________                               (17)

z = 0, m⁹—l.

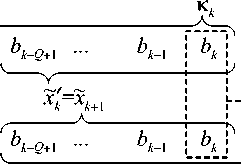
•> решение: b_k

Рис. 2. Принятие решения в пользу символа b_k на фоне комбинаций и состояния

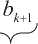
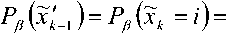
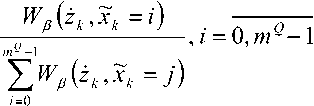
Произведение согласно (9) примет вид

w^k,Ai ,xk) = W(zk,zki],xk+] =i)=

= ^« ^k, x_k+A = z) Wp (z_k+], x_M = z),    (19)

i = 0, m ⁹ -1.

Определ и м слагаемые в сумме (2). Количество состояний ■^ к ’ содержащих конкретное значение символа ^k ⁵ в m раз меньше общего количества состояний в этот момент времени и равно m , тогда

Рассмотрим функции ПВ W^kVk^b^ и w(z_k+}\x_k+},b_k+}\ приведенные в выражениях (5) и (6). Обе функции эквивалентны. К ожидаемому сигналу v , полученному некоторой комбинацией символов в сдвиговом регистре размером 5 + 1 элементов (рис. 1), добавляется вектор шума и на входе приемника фиксируется отсчет сигнала “k . При условии, что шум является белым гауссовским, ПВ распределения сигнала z_k равна [6]:

w^k\xk,bk)

exp’i+

Q

2 A

^k-TAA-u • (23) /=0

Wti^Atub, =. = E^-’^+i’

^ 1 (20)

ПВ w^k^kti,bk =z) может быть использо- вана в определении как «жесткого» решения

Здесь O"^ – дисперсия белого гауссовского

Q шума, УЛАк-и – ожидаемый сигнал, кото-

„       '=0                                                       .

рый получается как сумма отдельных i-ых составляющих среза (см. рис. 3) импульсных характеристик канала, умноженных комплексно на значение сигнала йь . Каждое такое умножение соответствует символу ^k-i > находящемуся в сдвиговом регистре, а вся последовательность символов, ограниченная данной суммой, будет представлять комбинацию Кк '

2к-е	“bt-Q	gk-O,0	Sk-QA •	" - - - a - срез ИХ • ^ x "gk-QS 1
Zk-1	4-	gk-1,0. "	Xgk-1, V	• •     gk-LQ
	иьИ
Zk^	L*		' SkA •	• •       gk.Q
	Ubt	\gkS^ '

Рис. 3. Срез импульсных характеристик

При компьютерном моделировании важно правильно учитывать отношение «сигнал-шум» Е_{с 2}

N ’ которое обозначается как h [7]. Можно расписать его через мощность сигнала Р_с и шума Р.=р„

/,= 4 ₌ EL ₌ E_{FT :}^fe FJ. R ш ⁷ ш ⁷ ш ш

F здесь Ес – энергия ненулевого сигнала, соответствующего информационному элементу; 2V0 – спектральная плотность мощности шума; T – величина тактового интервала, в течение которого передается сигнал, соответствующий информационному элементу; Рд – частота дискретизации; а F – шумовая полоса частот, обычно совпадающая с верхней частотой сигнала.

В [7] исследовано, как рассчитывать дисперсию шума для различных вариантов отношения «сигнал-шум» и разных вариантах многолучевости в канале связи при компьютерном моделировании.

Переходя к отсчетам сигнала и шума, можно записать

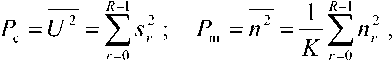
где R – число рабочих отсчетов сигнала на интервале T . При моделировании удобно нормировать мощность сигнала на передаче р,=УР=' для расчета параметра ^0 или на приеме

Р_С=^=Х для расчета параметра h . Кроме

'-°                                        I-----т того, можно не учитывать множитель 1/V2^ , а при вычислениях использовать логарифмы от ПВ и вероятностей.

При решении задачи уменьшения вычислительной сложности нормирование согласно (15) и (18) может быть проигнорировано, и вместо вероятностей могут использоваться соответствующие ПВ. При рекуррентных вычислениях оба направления, согласно обозначениям а и Р , рассматриваются независимо друг от друга. Но в обоих случаях выражение ^w^k\^k^k)^p{^bk) вычисляется одинаково. Поэтому, прежде чем приступать к рекуррентным вычислениям, можно сформировать двумерный массив данных, соответствующий значениям выражения ^wkz_k\x_k,b_k^b^ для всех т вариантов ^хк ^{и Ь}к , и для всех к = 1,г.

Выражения (3)-(8) показывают зависимость совместных ПВ и вероятности нахождения системы в соответствующем состоянии, с одной стороны, от предшествующих элементов, и с другой стороны – от последующих. При передаче двоичных символов (т = 2) для памяти Q = 2 взаимосвязи между рассмотренными функциями ПВ и вероятностями показаны на рис. 4.

Если в передаваемом сообщении информационный блок окружен известными символами, то можно определить так называемые стартовые моменты времени. Это означает, что в сдвиговом регистре могут находиться известные информационные символы. Стартовый момент времени необходим для установки начальных значений в приведенных зависимостях.

Самый ранний стартовый момент времени ^ = 0. Поздний стартовый момент времени для обратного направления Р зависит от памяти канала и равен k = B + Q + \. В [3] момент времени k = B + Q обозначен как т .

Начальные значения р(хо =z) и р(л-г. =/), i = 0,mQ -1 определяются исходя из содержимого сдвигового регистра в указанные моменты времени. Если в сдвиговом регистре все символы известны, то вероятность состояния с номером, который образуют символы в сдвиговом регистре, равна единице. Вероятность других состояний равна нулю. Если некоторые символы все-таки неизвестны, то стартовые вероятности состояний если все символы

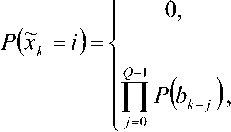
bMvj = 0,2-1 неизвестны, иначе,

Z - 0, 777 9 - 1.

Здесь

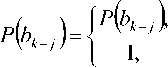
если символ b_k ■ известен, иначе.

Выводы

Математическое описание алгоритмов, как в [1], так и в данной статье, создает единую основу и возможность описания их уникальных реализаций для дальнейшего синтеза и анализа, а также дополняет материал к общему взгляду на рассмотренные алгоритмы АВ и АКН. Любая граничная группа символов до начала информационного блока и после него позволяет однозначно реализовывать данный способ демодуляции.

Единая запись для демодуляции m -позиционного сигнала позволяет анализировать произвольные линейные виды модуляций, в том числе и с основанием т > 2 . Приведенное математическое описание алгоритмов позволяет быстро и эффективно переходить к их программированию на любой платформе.

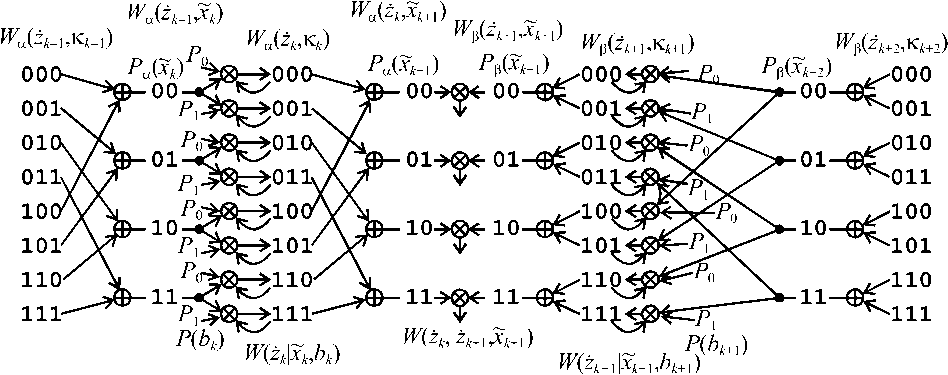
Рис. 4. Взаимосвязи между функциями ПВ и вероятностями при т = 2 ; 5 = 2