Математическая и компьютерная модели формирования потока заказов в сбытовой системе предприятия

Организационная структура сбытовой системы предприятия по выпуску автомобилей представляет собой систему продажи, субъектами которой являются связанные между собой материальными и информационными потоками дилеры по продажи автомобилей и покупатели [1-4]. Дилерские фирмы включены в состав предприятия, располагают складом готовой продукции, формируют заказы на автомобили со стороны покупателей и осуществляют поставки изделий и реализацию заказов. На поведение потребителей большое влияние оказывает величина запаздываний в потоках, поэтому для оценки динамических характеристик сбытовой системы необходимо определить время запаздывания в материальных и информационных потоках.

Схема информационных и материальных потоков в производственно-сбытовой системе представлена на рисунке 1.

На схеме представлены два основных потока производственно-сбытовой системы предприятия:

• – поток заказов (пунктирная линия);

  – материальный поток изделий (сплошная линия).

МОДЕЛЬ ФОРМИРОВАНИЯ УРОВНЯ НЕВЫПОЛНЕННЫХ ЗАКАЗОВ

Поток заказов со стороны покупателей к ди леру и поток заказов со стороны дилера в произ- Кобенко Александр Владимирович, исполнительный директор.

водство характеризуются величиной скорости потока заказов VRR (At), VRD (At). Материальные потоки изделий от производства к дилеру и от дилера к покупателям характеризуются величиной скорости потоковv^(At) и Vss(At).

Для моделирования системы введены следующие обозначения

Xuoto – объем потока невыполненных заказов в сбытовой системе;

^vrr(A1) – величина скорости входящего потока заказов на изделия со стороны покупателей;

v^(At) – величина скорости входящего потока поставки изделий в сбытовую систему из производственной системы предприятия;

v^s(At) – величина скорости исходящего потока отгрузки изделий покупателям;

^Df(At) – величина запаздывания в процессе реализации заказов в сбытовой системе;

^(t) – фактический запас в сбытовой системе;

ax –начальные условия.

Сравнивая величины скоростей входящего потока заказов с величиной скорости исходящего потока отгрузки изделий можно определить объем невыполненных заказов в сбытовой системе, а сравнение величин скоростей потоков поставки изделий с потоком отгрузки изделий покупателям можно определить величину уровня запасов изделий на складе дилера. С учетом введенных обозначений модель формирования уровня невыполненных заказов с учетом величин скоростей потоков будет иметь следующий вид:

x5o(t + At) = x^o(t) + At(v^R(At) - v^s(At)),

Vgs(At) = ^^^-.v^CAt) = const, (1)

"DF

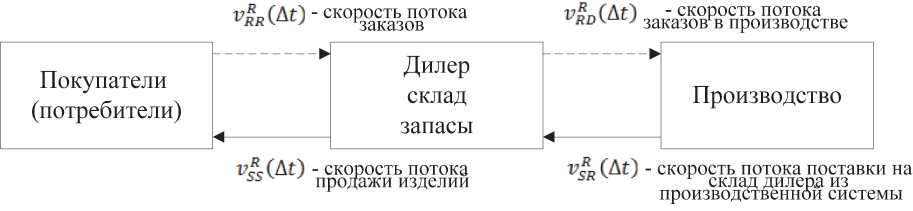
Рис. 1. Схема потоков в производственно-сбытовой системе предприятия

х£₀(°) = ^х^оСО >  0, At = 0,1,2

Предположим, что в дискретной динамической модели (1) величина разности между скоростями потоков заказов и потока отгрузки изделий покупателям больше нуля (v^R(At)-v^(M))>0. Это неравенство означает, что величина скорости потока формирования заказов VRR(At) превышает величину скорости потока отгрузки изделий покупателям Vss(At). При выполнении этого неравенства объем невыполненных заказов увеличивается с каждой итерацией и в установившемся режиме скорость потока отгрузки изделий покупателям становится равной заданной скорости формирования заказов, т.е. VrR( At) = ^(Д€), а разность{vJKM-v’Ut))=0. Умножая величину разности между скоростями потоков

At на интервал времени , получаем объем невы- полненных заказов, характеризующий уровень синхронизации между двумя потоками vrr(^0 и v^(At). Произведение продолжительности интервала времени At на скорость входящего потока заказов со стороны покупателя определяет объем заказов полученный за интервал At. Аналогично, произведение At(v£s(At)} представляет собой объем реализованных заказов покупателям в течении интервала At . В случае, когда величина разности между скоростями потоков заказов и потока отгрузки изделий покупателям является отрицательной величиной, т.е. (vRR(At) -v^s(At))< 0, то умножая эту величину разности на интервал времени At, получаем объем запасов на складе у дилера. Полу- ченное неравенство означает, что величина скорости отгрузки изделий покупателям VsS(At) больше скорости формирования потока заказов vRR(At), т.е. v^(At) > vRR(At). Это означает, что в системе не производится отгрузка изделий покупателю, а величина запасов увеличивается с учетом отрицательной разности между потоками .

Представленную модель формирования объема невыполненных заказов реализуем с использованием пакета прикладных программ

Matlab, с помощью средств моделирования динамических систем Simulink [5]. На рисунке 2 изображена дискретная динамическая имитационная модель формирования объема невы- полненных заказов.

Входной сигнал в модели представляет собой величину скорости потока заказов от покупателей, характеризующий спрос со стороны потребителей на изделие. Данный сигнал является заданной установкой, поступает на сумматор в котором вычисляется разность между скоростями потоков заказов и потока отгрузки изделий покупателям(v^Atj-v^At)), являющейся величиной невыполненных заказов которая поступает на дискретный интегратор, выходом которого является искомая величина Хц0 (t) равная объему потока невыполненных заказов. Блок saturation учитывает ограниче- ния на величину потока невыполненных заказов XUO ("0 — 0. Таким образом имитационная модель представленн6ая на рисунке 2 совместно с математической моделью (1) представляет собой электронный макет блока формирования объема невыполненных заказов в торговой системе, позволяющего с учетом различных производственных ситуаций синхронизировать потоки заказов со стороны покупателей VRR(At) с потоком отгрузки изделий потребителям VsS(At) .

В таблице 1 представлены расчетные и имитационные результаты полученные по модели (1) с учетом следующих исходных данных:

1400 шт.; Vrr (At) = 1500 шт./нед.; At = 0,1 недели.

С учетом исходных данных дискретная модель (1) потока невыполненных заказов имеет следующий вид:

X^o(t + At) = x^0(t) + 0,1(1500 - vsRs(At)),

R                                    znx

VSslMJ — -----,          (2)

x^_o(0) = 1400₇x^_o(t) > O_f At = 0,1,2

Результаты расчетов по модели (2) представлены в таблице 1.1.

Из таблицы 1 следует, что результаты расчетов по модели (2) и по дискретной динамической модели (рисунок 2) совпадают, что

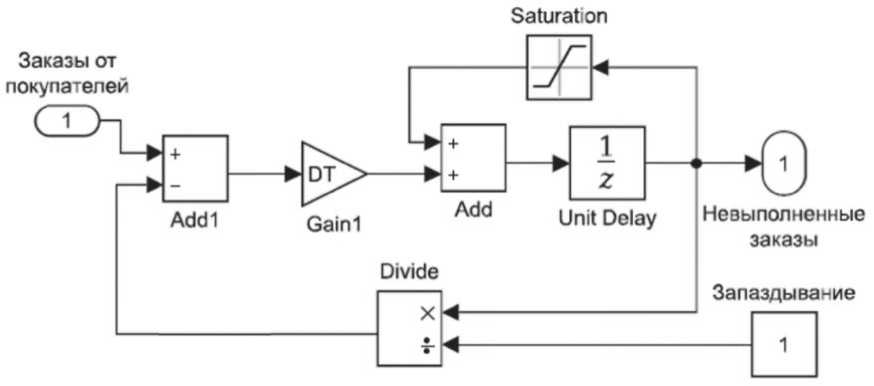
Рис. 2. Имитационная модель формирования объема невыполненных заказов

Таблица 1. Сравнение расчетных и имитационных данных по формированию объема невыполненных заказов

Объем невыполненных заказов (расчет по имитационной модели)	Скорость потока отгрузки изделий потребителям (расчет по имитационной модели)	Объем невыполненных заказов (расчет по формуле)	Отклонение ст.1-ст.3
х ио (t)	V sR (At)	XR o (0 f^ tR^ti — V SS (^t)) = a R + At^--------------
1	2	3	4
1400,00	777,7777778
1436,11	792,1014355	1436,11	0,00
1471,51	805,9047491	1471,51	0,00
1506,21	819,223254	1506,21	0,00
1540,25	832,0904635	1540,25	0,00
1573,65	844,5368302	1573,65	0,00
1606,42	856,5891027	1606,42	0,00
1638,59	868,2700144	1638,59	0,00
1670,18	879,5982358	1670,18	0,00
1701,20	890,5885274	1701,20	0,00
	...	...
		...
3706,74	1506,565155	3706,74	0,00
3706,41	1510,806816	3706,41	0,00
3705,87	1515,005969	3705,87	0,00
3705,12	1519,162854	3705,12	0,00
3704,16	1523,27767	3704,16	0,00
3703,00	1527,350577	3703,00	0,00
3701,63	1531,381692	3701,63	0,00
3700,06	1535,371086	3700,06	0,00

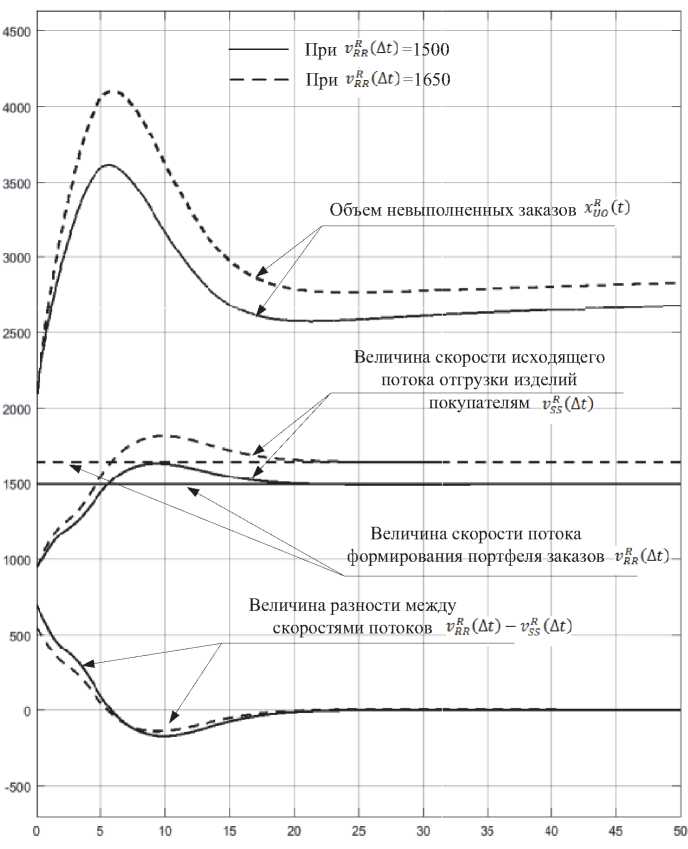
Рис. 3. Графики траекторий изменения параметров модели формирования объема невыполненных заказов

позволяет обосновать результаты расчетов имитационного моделирования.

На рисунке 3 представлены траектории изменения во времени объема невыполненных заказов ";: :■, графики величины разности между скоростями потоков заказов и продаж ; ’. г- >■ - ■.— 17- :, графики траектории изменения скорости потока отгрузки изделий потребителю v:'7 17- и график скорости потока формирования заказов vi'- 17-. Пунктирные линии траекторий соответствует ситуации, когда величина скорости формирования заказов (спрос) "Г- .^7- увеличена на 10% относительно установившегося значения равного 1500 шт./ нед. Из графика траекторий следует, что невыполненные заказы в начальный период растут до максимально значения равного 3600 шт. в неделю, а затем при времени 7 = с нед. умень-шаютя до установившегося значения. Уменьшение объема невыполненных заказов объясняется тем, что разность между скоростями

^R(At) -v^s(At)j потоков становится отрицательной с момента времени " = ^ нед. и далее эта величина стремиться к нулю, поскольку величина скорости потока заказов достигает заданной скорости потока отгрузки изделий потребителю равной 1500 шт./нед. Таким образом, расчетные траектории потоков в полной мере характеризуют динамические характеристики параметров дискретной динамической модели (1) по определению объема невыполненных заказов.

Отметим, что в модели (1) скорость потока заказов ".г- 17 -принята постоянной величиной, однако как показывает практика скорость потока заказов со стороны покупателей "Г- 17-колеблется во времени и имеет случайный характер изменения, возникает необходимость в усреднении потока информации о заказах в сбытовую систему. Процедура усреднения требует определенного времени накопления данных, что порождает в системе время запаздывания информационного потока. Таким образом, усреднение данных о величине текущего потока заказов со стороны покупателей осуществляется за определенный период времени. Чем больший период времени требуется для усреднения величины заказов, тем больше величина запаздывания в системе. В этой связи процедура усреднения является важной характеристикой динамики изменения параметров сбытовой системы. Результаты процедуры усреднения пред- ставим в виде следующего дискретного динами- ческого уравнения:

VR_S(t+ At) = v£_s(t) + At(4-) (vr_R(AI) - v£_s(t)) vnOR/ V                  /

^(At) > 0, (At) = 0,1,2..., где VrS№ – средняя скорость потока заказов со стороны покупателей в сбытовую систему; ^dr – время запаздывания у дилера, необходимое для реализации процедуры усреднения заказов, поступающих от покупателей.

Сформированное уравнение позволяет определить усредненную скорость продаж изделий на каждом временном шаге.

На рисунке 3 представлена дискретная динамическая имитационная модель, сформированная в соответствии с математической моделью

(2) по определению усредненной скорости потока заказов со стороны покупателей в сбытовую систему. В качестве входного сигнала скорости потока заказов принятая случайная величина со следующими характеристиками: среднее значение сигнала - 1500 шт.; среднеквадратическое отклонение - 100 шт.; время запаздывания, необходимое для выполнения процедуры усреднения, принято в двух вариантах - 0,1 и 0,5 нед.; шаг интегрирования At = DT = 0,05 нед.; начальное условие скорости потока Vrr(0) = 1300 шт.

На рисунке 4 и рисунке 5 изображены траектории скорости изменения потока заказов и его усредненная величина при времени запаздывания равном - 0,1 и 0,5 нед. Сравнивая процедуры усреднения при различном времени запаздывания, можно сделать вывод, что чем больше величина запаздывания, тем больше требуется времени на достижение среднего значения случайного потока заказов со стороны покупателей в сбытовую систему.

ЗАКЛЮЧЕНИЕ

Приведенные результаты моделирования системы формирования невыполненных зака-

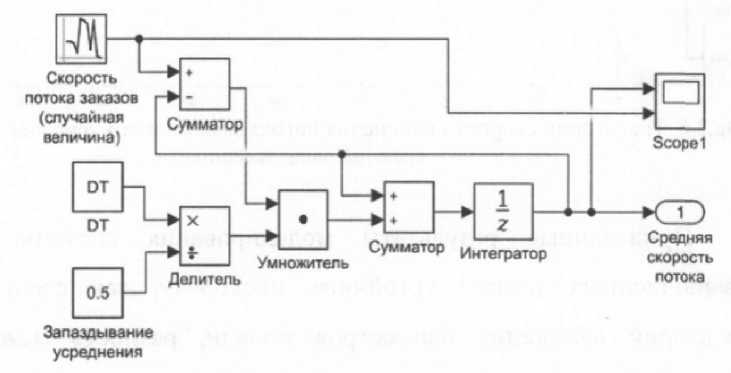
Рис. 4. Дискретная динамическая имитационная модель усреднения скорости потока заказов со стороны покупателей в сбытовую систему

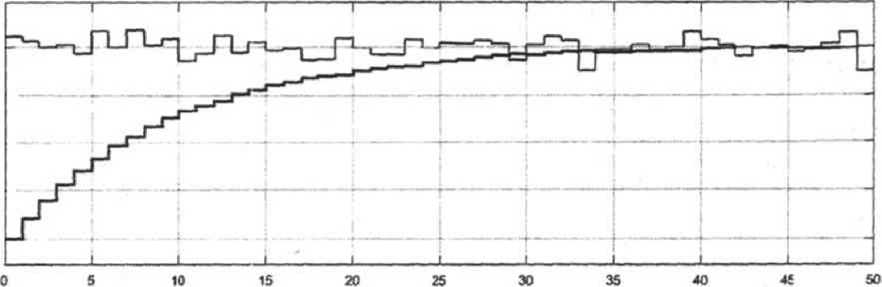
Рис. 5. Траектории скорости изменения потока заказов и его усредненная величина при времени запаздывания 0,5.

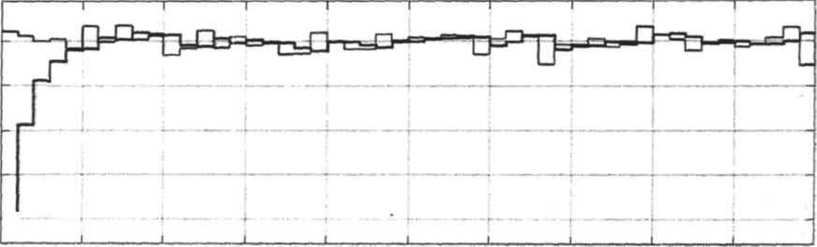
Рис. 6. Траектории скорости изменения потока заказов и его усредненная величина при времени запаздывания 0,1

зов устойчива, поскольку, как следует из графика траекторий изменения параметров модели, разность между скоростями потока заказов и потока отгрузки изделий покупателям стремится к нулю, а объем невыполненных заказов к стабильному уровню.

Рассмотрим задачу оценки чувствительности объема невыполненных заказов к изменению величины запаздывания ^DF. Для этого продифференцируем уравнения модели (1) по параметру ^DF, в результате получим следующее уравнение чувствительности:

•Cat)

to

X

Скорость отгрузки

Временно*

интегрирования

Скорость потока

Запаздывание выполнения дилером

Эластичность объема невь-полненных невыполненных

Чуэстви’ельнэсть объема невыполненных заказов

Рис. 7. Дискретная динамическая имитационная модель определения чувствительности и эластичности объема невыполненных заказов к изменению параметра hop (^t)

_TIhpp(4t) z х 3xuQ(t+At)

где %W ^ dhyp (At) – коэффициент чувствительность объема невыполненных заказов к изменению параметра hop(At) в момент времени t;

hop(at) , x     hppUt) — —

M W          – коэффициент эла-

^uoto      xQ0(t+zto стичности объема невыполненных заказов к изменению параметраhcp(^t) в момент времени t.

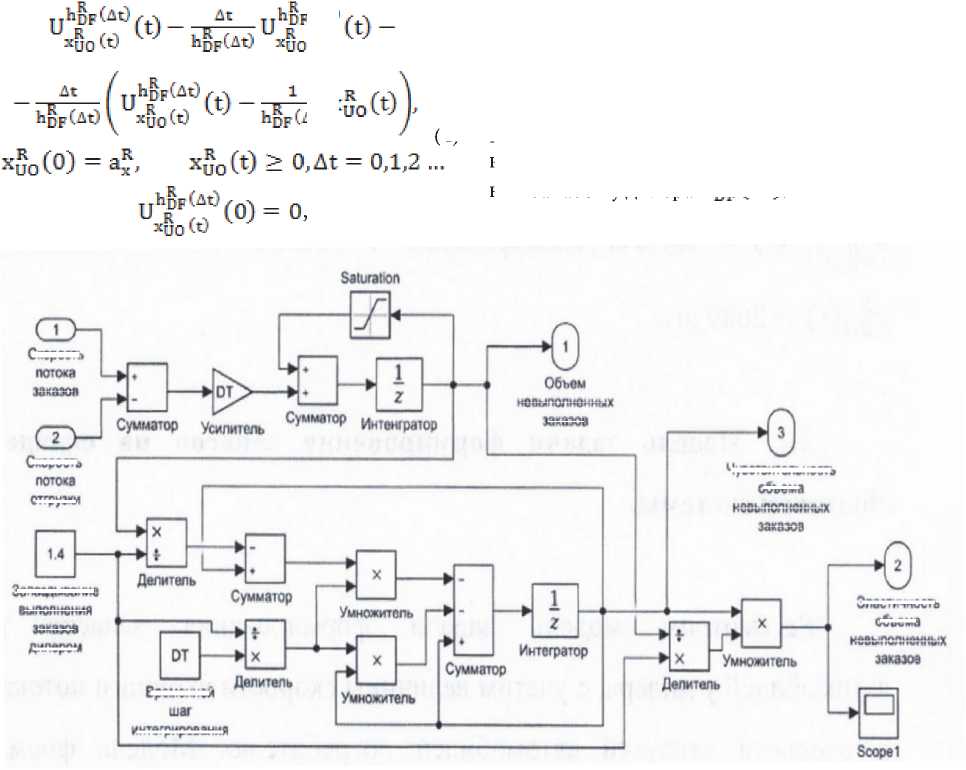
На рисунке 7 представлена дискретная динамическая имитационная модель определения чувствительности и эластичности объема невыполненных заказов к изменению параметра hopC^ti, полученной в результате совместного решения системы уравнений (3) и (4).

На рисунке 8 и рисунке 9 изображены траектория изменения объема невыполненных заказов и траектория изменения его эластичности к параметру величины запаздывания выполнения заказов у дилера ^df (At).

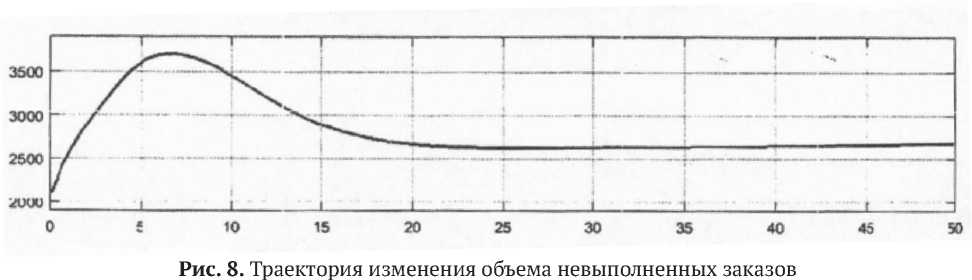
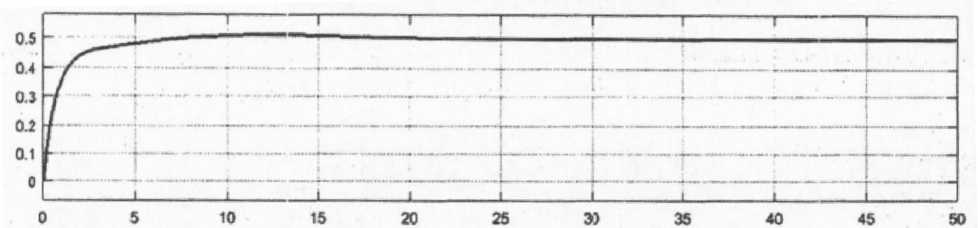
Рис. 9. Траектория изменения эластичности объема невыполненных заказов к параметру величины запаздывания hop С^)

Как следует из рисунка 9, с ростом величины запаздывания в начальный момент времени, увеличивается объем невыполненных заказов. Коэффициент эластичности достигает hop(At) , установившегося значения равного . R W xuo to

= 0,4996, одновременно с объемом невыполненных заказов Xro (t) =2689 шт.