Математическая модель адиабатного течения

Течение одномерное.   Фазовые переходы жидкость-пар начинаются в метастабильной области состояний. Жидкая фаза в гетерофазном потоке находится в перегретом состоянии.Паровая фаза в гетерофазном потоке находится в насыщенном состоянии.

Фазы движутся с одинаковыми скоростями. Учитывается трение только жидкой фазы о стенку канала. Обоснование допущений. Допущение об одномерности течения не оказывает существенного влияния на энергетические характеристики потока. Расчетные значения скорости, будут отличаться на 1-3 % от истинных в меньшую сторону на периферии потока и в большую - в центре струи. Основной недостаток одномерной схемы течения в том, что она не отражает структурной неоднородности гетерофазного потока.

Допущение об адиабатности процесса предполагает пренебрежение теплообменом потока с окружающей средой. Принимая во внимание то обстоятельство, что энтальпия жидкости намного больше того количества тепла, которое передается потоку через стенки канала за счет теплопроводности, допущение об адиабатности процесса не является грубым.

Допущение о зарождении паровой фазы в метастабильной области состояний соответствует теоретическим и экспериментальным сведениям об условиях фазовых переходов в реальных системах жидкость-пар.

Допущение о равенстве скоростей фаз в общем случае не соответствует действительности. Расхождение будет существенным в дисперсной области потока, где несущей средой является пар и по мере увеличения длины канала разность скоростей увеличивается. В литературе имеются сведения, что при пузырьковой структуре потока скорости фаз практически совпадают.

В дисперсном потоке жидкая фаза будет двигаться медленнее по сравнению с паровой фазой. Разность скоростей, обычно выражаемая коэффициентом скольжения К = W. [W_c, зависит от градиентов давления и колеблется в диапазоне значений К=1,2-1,8. Пренебрежение скольжением фаз при массовых паросодержаниях жидкости х <0,9 мало сказывается на точности расчетов параметров потока.

Уравнения сохранения. С учетом принятых допущений уравнения сохранения массы, количества движения и энергии примут вид:

1       Г dpn  (       \Ф (л   \рр^ 1  1 dw 1 dF „ ф+ (рп — рж)+ (1 — ф)+1— 0

фрп +(1 — ф }рж [ dz            dz         dz _|  W dz F dz dW        dWdP

ФР-WT" ^{+ ( 1 —} Ф ⁾P■^W_I + , + Ф p ^{— 0}

dz             dzdz di•          d›        diсdW x--+ (i, — i )+ (1 — x)+ W— 0

dz         dz        dzdz

В системе уравнений (1) плотность и энтальпия двухфазной среды определяется на основании свойств аддитивности через паросодержание и параметры состояния фаз.

Сила трения жидкой фазы о стенку канала определяется согласно рекомендациям из уравнения: ф

_ ^e f р ж w

2 d

, где коэффициент трения

1 равен: c_f — --------------^.

f   ( 0,812lnRe — 1,64 ) ²

Система уравнений (1) замкнута, если известны геометрия канала

F=F(z) и термодинамические свойства фаз, включая и метастабильную облаеть еоетояний: T=Ts(P), рп=рп(Т), рж=р(Т) ,in=in(T), in*=i(T*), L=L(T), L*=L(T*), где ^-параметры жидкоети в метаетабильной облаети еоетояний при перегреве AT=f(n), доетижимом в процееее адиабатного расширения жидкости.

Для нахождения свойств фаз и коэффициентов аппроксимирующих функций удобно использовать пакет прикладных программ "Жидкость-пар", разработанный в лаборатории термодинамики кафедры ТОТ. Свойства фаз на линии насыщения определяются следующими однопараметрическими уравнениями.

Плотноеть жидкоети: р — р _р [ а_о • ( 1 — т ) а ¹ + 1 ] ,                (2)

Плотность пара:

P s ^—

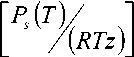
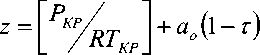
Температура на линии наеыщения: T_s — Т_к ^^ а ,. (1 — ln п ) i ,    (4)

i — 1

Давление насыщенных паров: р = P_p • exp [ a ₀ + a_x (V т ) + a ₂ ln т + a₃ т ] , (5)

Энтальпия насыщенных паров: i. = RTKДа0 + ахт + а2т2)

,

Скрытая теплота парообразования: L = RTKра0 (1 - т)а1,(7)

Динамическая вязкость: п = a • exp(aV^ j,(8)

Поверхностное натяжение: а = <г0а0 (1 - т)a1,

В уравнениях (2-9): Na- число Авогадро, ц- молекулярный вес, (p_кр, Р_кр, Т_кр) - параметры вещества в критической точке.

Численное интегрирование системы уравнений. Разрешим систему уравнений (1) относительно производных по давлению, скорости и паросодержанию,      предварительно      выполнив      операции дифференцирования. Принимая во внимание уравнение связи между массовым и объемным паросодержанием. x = ^рп/рж и выражая энтальпию жидкости через энтальпию пара и скрытую теплоту парообразования i = (i. - L), систему уравнений сохранения приведем к виду:

dP  1 dW    dp      dPdW

U 11   +      + U13   = U14,    + pW dz  W dz      dz        dzdz

U_3idP + wdW + U„d p = 0 , ³¹ dz      dz     ³³ dz

где для краткости записи введены обозначения: Yo = x = ppjp,(11)

Y = ₉ ^p + ( 1 - _Ф ) -Pk

¹     dP        dP

d p . ф ФР ^

Y ² =                 2 • ^Y 1

dP p p

U _u = Yd p ,

^U 13 = ⁽ p . — p c )/ Р ^,

U 14 =

1 dF

F dz ,

^U 31 = Y 2 i . ^{+ Y} 0 ” ^{+ ( 1} — ^Y 0 dP

^“

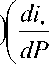
dL )- Y (й - L ,) , dP J    ^{V      7}

и 33 = Y 3 ( i. - i. * + L * ) •

Алгоритм расчета должен включать условие критического течения, градиент

значение,

линейных

при котором расход стремится к критическому, G^G_Kp и давления по всему тракту канала имеет отрицательное dP

— (0. Метод решения. Численное интегрирование системы dz дифференциальных уравнений осуществлялось методом Рунге-

Кутта. Алгоритм расчета включает условие критического течения, при котором расход G^Gkp и градиент давления по всему тракту канала dP имеет отрицательное значение —(0. Метод решения - ^’пристрелка по dz расходу". Для этого при заданных начальных параметрах потока рo и To задается максимально возможный расход G^ = F( [2рт0 ]0,5 и минимально возможный расход Gmin=0. Критический расход подбирается в интервале dP

Gmin