Математическая модель агломерации твёрдой дисперсной фазы в циклоне с жидкостно-капельным орошением

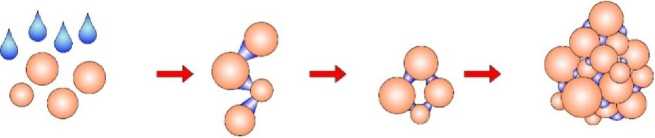
Современные тенденции получения пищевых порошков доказали целесообразность использования многостадийных распылительных сушильных установок с возвратом высушенной высокодисперсной фракции из циклона (далее твердые частицы) в область диспергирования с целью получения агломерированных частиц (рисунок 1) и последующим их досушиванием[1-3].

Разработка эффективных технологических схем производства быстрорастворимых порошкообразных пищевых материалов требует не только разработки нового оборудования, способного интенсифицировать процессы сушки и агломерирования [3, 4], но, и теоретического обоснования происходящих при этом массообменных процессов.

Распыление Spraying

Увлажнение

Humidification

Затвердевание Готовый агломерат Solidification Ready agglomerate

Порошок* жидкость Жидкие мостики Powder+liquid Liquid briges

Твёрдые .мостики Solid briges

Структура "Ежевики" "BlackBerry " structure

Рисунок 1. Схема образования агломератов увлажнением сухих частиц

Figure 1. Scheme of formation of agglomerates during wetting of dry particles

Физическая модель получения быстрорастворимых порошков показана на схеме (рисунок 2), которая предполагает, что твёрдые частицы в виде газовзвеси подаются в кольцевой зазор коллектора 4 где газовзвесь закручивается и, проходя через равные по площади щелевые зазоры между лопатками 5, рассекается на равные потоки, образуя вихрь во внутренней части коллектора 4 направленный к его оси. Для механической агломерации суспензия продукта с помощью распылителя 3 диспергируется внутри коллектора 4, непосредственно в уже упомянутый вихрь газовзвеси для столкновения диспергированных частиц жидкой фракции продукта и сухих твердых частиц из газовзвеси. Газодинамика коллектора 6 организована таким образом, что достигается высокая интенсивность образования агломератов и исключение контакта диспергированных влажных частиц с внутренней поверхностью коллектора, образованной лопатками 5. При дальнейшем движении влажных высокодисперсных частиц и агломератов предполагается удаление избытка растворителя конвективной сушкой в конической 6 и цилиндрической 7 частях сушильной камеры и дальнейшее отделение сухих твердых частиц для последующего агломерирования [5].

В [6] отмечается, что получены результаты по локальному взаимодействию частиц, а также математическое описание формирования агломератов в масштабах аппарата в целом практически отсутствует.

Отсутствие корректного теоретического обоснования схем агломерации в масштабах установок делает невозможным рациональный выбор технологических режимов и конструкторских решений, а уже накопленный опыт реализации подобных схем [7] позволяет сделать вывод об актуальности проблемы.

Для анализа предложенной схемы рассмотрим циклонную камеру для агломерации твёрдых частиц, поступающих с тангенциальным вводом газовой несущей среды и с орошением закрученного потока дисперсной жидкостью распыливаю-щей форсункой (рисунок 2). Картина агломерации в этом случае такова: твёрдые частицы сталкиваются с каплями жидкости, смачиваясь при этом; твёрдые частицы с плёнкой жидкости на поверхности в силу турбулентных пульсаций дисперсионной среды при соприкосновении удерживаются силами поверхностного натяжения жидкости. Многократное повторение такого процесса приводит к укрупнению частиц и к получению их агломератов.

Для теоретического описания физической картины использование фундаментальных уравнений переноса импульса (уравнение Навье-Стокса) и массы (уравнение конвективной диффузии) затруднительно по причине неясности в постановке условий на границе раздела фаз и стохастического характера столкновения твердых и жидких частиц в флуктурирующем турбулентном потоке несущей газовой среды [8, 9].

Поэтому для построения модели совокупных процессов в циклонной камере применим принцип аналогичный с химическими превращениями в рамках кинетических превращений. Будем обозначать твёрдые частицы, поступающие в циклонную камеру, через субстанцию А, а рас-пыливаемые форсункой капли раствора через субстанцию В. Соединение субстанций А и В приводит к образованию новой субстанции S (твёрдые частицы с плёнкой на поверхности):

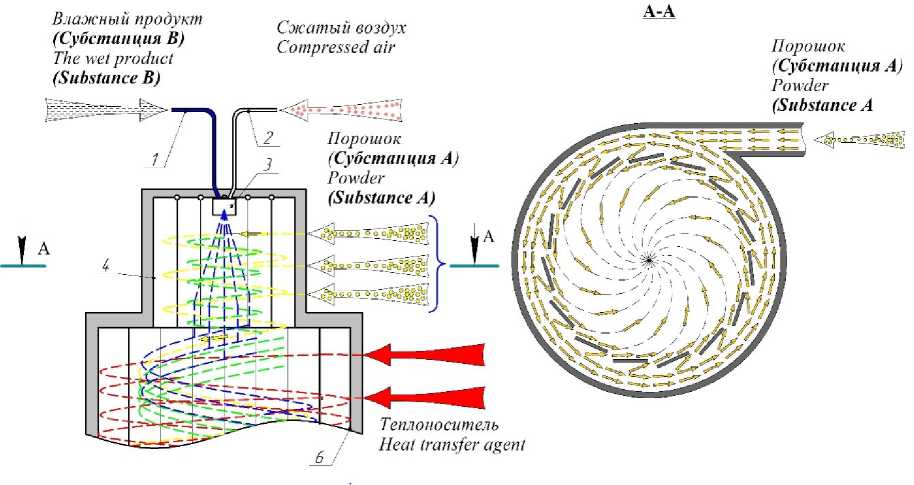
Рисунок 2. Схема агломерации в башне распылительной сушилки:1 – патрубок подачи жидкого продукта, 2 – линия подачи сжатого воздуха, 3 – пневматическая форсунка, 4 – коллектор, 5 – лопатки, 6 – коническая часть сушильной камеры, 7 – цилиндрическая часть сушильной камеры

Figure 2. Agglomeration scheme in the tower spray dryer: 1 – supply of the liquid product nozzle, 2 – the compressed air line 3 – pneumatic nozzle, 4 – collector, 5 – vane, 6 – a conical part of the drying chamber, 7 – the cylindrical part of the drying chamber

A + B —^ S ,         (1)

Причём кинетика этого процесса определяется кинетическим коэффициентом k 1 . Превращение по соотношению (1) описывается системой уравнений гетерогенной химической реакции со стохастическим единичным эквивалентом, т. е.:

dCAT) = - kx Ca (t) CB (t);(2)

dt dC^) = - k1CA (t) Cb (t);(3)

dt dC^ = - kx Ca (t) Cb (t);(4)

где t – текущее время; C A (t) , C B (t) , C S (t) – концентрации субстанций соответственно А , В и S .

Процесс образования агломератов, которые обозначим через субстанцию C , протекает по схеме соединения:

S + A —^ С,(5)

где k 2 – кинетический коэффициент, характеризующий скорость протекания этого процесса. В соответствии с (5) запишем:

dC^ = - k2 Ca (t) Cs (t);(6)

dt dC# = - k2 Ca (t) Cs (t);(7)

dC^t) = k2 Ca (t) Cs (t);(8)

dCA^t) =—2Ca (t)[kxCb (t)+ k2Cs (t)];(9)

dCB^t) = -kxCA (t)Cb (t);(10)

dCS^tl =-2Ca (t)[kxCb (t) + k2Cs (t)];(11)

dCC^tl = k2 Ca (t) Cs (t);(12)

Свяжем полученную систему кинетических уравнений (9)–(12) с гидродинамикой в циклонной камере исходя из того, что вращающийся поток можно представить как поток идеального вытеснения, т. е. использовать соотношение u = z/f где z – координата в направлении закрученного потока, u – скорость потока; тогда система (9)–(12) запишется в виде задачи Коши:

udCd^z) =-2CA (z)[kxCB(z)+ k2Cs (z)];

udCdzz) = — kxCa (z)Cb (z);(14)

udCS^z) =2Ca (z)[kxCB (z)-k2Cs (z)];

udCC^z) = k2 Ca (z) Cs (z);(16)

с начальными условиями:

C a ( 0 ) = C a ⁰ ; C b ( 0 ) = C b ⁰ ;       (17)

C s ( 0 ) = C C ( 0 ) = 0;          (18)

Для анализа математической модели (13)–(18) запишем её в безразмерном виде, сократив при этом число определяющих параметров:

dX a ( Z ) dZ

=- 2 X a ( Z ) [ X b ( Z ) + K - X_c ( Z ) ] ; (19)

^^ =-Xa (Z)Xb (Z);(20)

dXS^Z ) = 2 X_A ( Z ) [ X b ( Z ) - K - X_s ( Z ) ] ; (21)

dXC^ = K - Xa (Z)Xs (Z);

с начальными условиями:

Xa (0) = 1, Xb (0) = £(23)

Xs (0) = Xc0 = 0;(24)

где:

Z = zk i C a ⁰ / u , X a ( Z ) = C a ( z ) / C a °,

X b ( Z ) = C b ( z ) / C a °, X s ( Z ) = C ( z ) / C a ⁰ ,

X c ( Z ) = C c ( z ) / C a °, ^ = C b °Z C a °, K = k ²Z ;

i

Система (19)–(24) относится к классу нелинейных и может быть проинтегрирована только численно, например, простейшим явным методом Эйлера по конечностно-разност-ной схеме:

X'a+1 = XA - 2XA (XB + K -XC )AZ;(25)

XB+ = XB - XAXB AZ;(26)

Xi,+1 = Xi, + 2X' fX' + K - X')AZ;(27)

S   S   ABs

Xi,+1 = Xi, + K - X'Xi AZ;(28)

C   CAS

XA = 1; XB = ^; XS = 0; X0 = 0; i = 0,1,_ ;

a                                      b                                     c

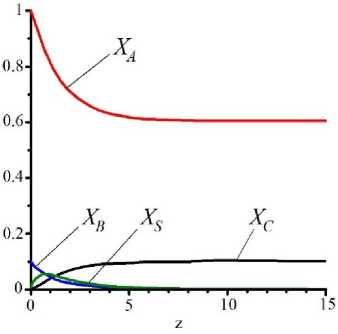
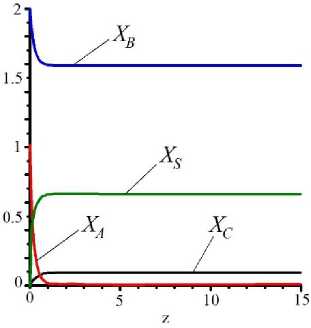
Рисунок 3. Кинетика процесса агломерации при К =1 и различных значениях ξ : a – 0,1; b – 1,0; с – 2,0;

Figure 3. The kinetics of the sintering process at К =1 and different values of ξ : a – 0,1; b – 1,0; c – 2,0;

a                                       b                                     c

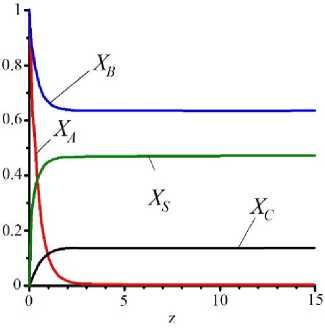
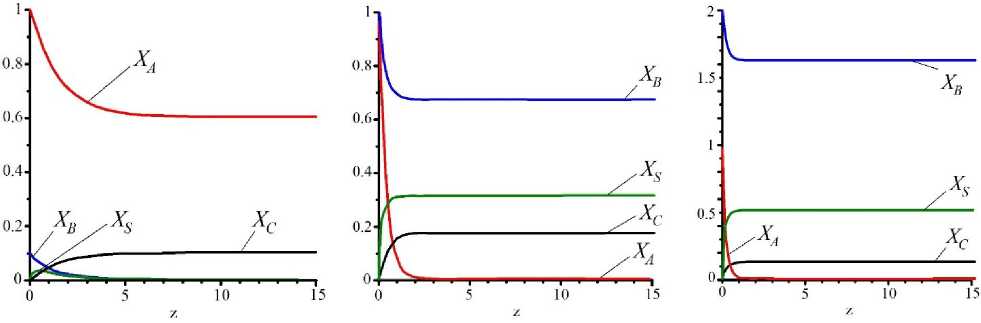
Рисунок 4. Кинетика процесса агломерации при К =2 и различных значениях 5 : а - 0,1; b - 1,0; c - 2,0;

Figure 4. The kinetics of the sintering process at К =2 and different values of ξ : a – 0,1; b – 1,0; c – 2,0;

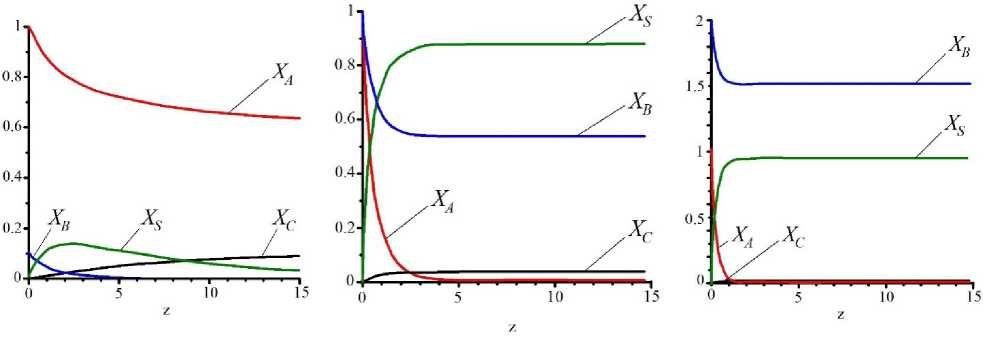
Рисунок 5. Кинетика процесса агломерации при К =0,1 и различных значениях $ : а - 0,1; b - 1,0; c - 2,0;

Figure 5. The kinetics of the sintering process at К =0,1 and different values of ξ : a – 0,1; b – 1,0; c – 2,0;

Реализация численного эксперимента выполнена в кодах математического пакета MAPLE – 15.

Расчёты показывают, что при равенстве кинетических коэффициентов процессов образования плёнки на частицах и агломерации наибольший выход агломерированных частиц наблюдается в случае одинаковых величин концентраций твёрдых частиц в газовзвеси и капель на выходе из орошающей форсунки (рисунок 3). Причём, величины агломератов достигали ≈15%, при значительном количестве мелких частиц ≈45%, но не с эффективным использованием капель раствора. Следует заметить, что затравочные частицы практически отработаны.

Если превалирует процесс агломерации над процессом создания плёнки на твёрдых частицах в циклонной камере (рисунок 4), то по-прежнему равенство концентраций твёрдых частиц и капель является наилучшим режимом в смысле получения максимального количества агломератов, при этом картина с остальными фракциями остаётся практически такой же, как и в случае, когда K =1.

Если наоборот, процесс нанесения плёнки на частицы является лимитирующим, по сравнению с их агломерацией (рисунок 5), то ситуация с образованием агломератов хуже, по сравнению с предыдущими вариантами развития процесса.

a

b

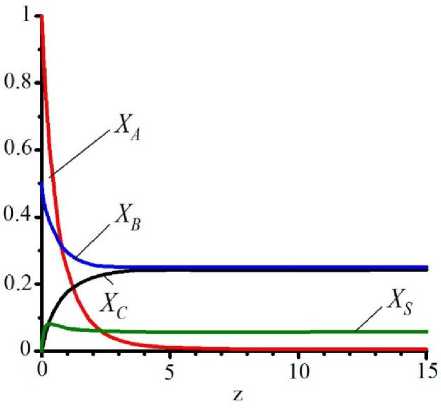
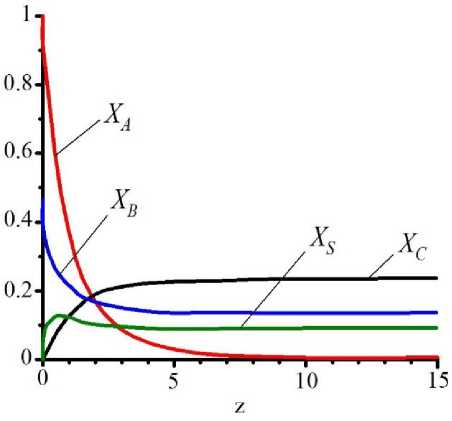
Рисунок 6. Вариант эффективных режимов агломерации: a – K =5; ξ = 0,5; b – K =2; ξ = 0,4

Figure 6. Alternative modes of effective agglomeration: a – K =5; ξ = 0,5; b – K =2; ξ = 0,4

Качественный анализ процесса агломерации показывает, что существуют эффективные режимы, но в области, когда k 2 >k 1 и C A⁰ > C B⁰ . Однако на практике реализация такого режима вызовет затруднения по причине первичности процесса образования плёнки на частицах (рисунок 6). Выход из данной ситуации заключается в разработке специальных узлов в распылительных сушилках, увеличивающих вероятность столкновения частиц за счёт