Математическая модель аграрного сообщества
Автор: Романова Александра Борисовна, Колпак Евгений Петрович, Андреева Ульяна Юрьевна, Полина Софья Геннадьевна, Шмелева Анастасия Анатольевна
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Сельскохозяйственные науки
Статья в выпуске: 1 т.7, 2021 года.
Бесплатный доступ
Разработана математическая модель роста численности населения аграрного сообщества, охватывающая 17 веков н. э. В модели учитываются два вида ресурсов, обеспечивающих жизнедеятельность, и влияние управляющих структур на рост численности населения. Аналитические результаты сопоставляются с оценочными данными историков и экономистов о численности населения мира. На основании статистического подхода предложена модель оценки возможной динамики роста численности населения.
Математическое моделирование, выживаемость, ресурс, устойчивость, дифференциальные уравнения
Короткий адрес: https://sciup.org/14117966
IDR: 14117966 | УДК: 51-76 | DOI: 10.33619/2414-2948/62/08
Текст научной статьи Математическая модель аграрного сообщества
Бюллетень науки и практики / Bulletin of Science and Practice
Социальная динамика многофакторная, многокомпонентная, имеет очень сложные внутренние связи, с трудом поддается формализации. Обращение к историческому прошлому позволяет оценить возможные варианты развития современного социального общества. Восприятие истории как череду каких-то фактов, сводит анализ исторических событий к описанию отдельных событий и деяний отдельных личностей и социально активных групп. Интегральные процессы в исторических документах не отражаются. То есть закономерный процесс взлета и падения цивилизаций, социальных и экономических формаций не всегда воспринимается как закономерный процесс. Человек находится на локальном микроуровне в социальной системе, и текущее макросостояние осознать не просто. Усилиями многих исследователей на сегодняшний день удалось установить отдельные исторические закономерности [1]. Одной из закономерностей является цикличность процессов, которые вызваны количественными и качественными внутренними изменениями в социальной самоорганизации общества, внешним влиянием со стороны иных социальных обществ, изменениями в среде обитания [2–3].
Объединение людей в социальные общество началось около 150 000 лет тому назад. Самоорганизация происходила в процессе коллективного изменения окружающей среды. При этом и среда обитания оказывала влияние на человека [4]. В экономическом плане первоначальные сообщества людей представляли собой общества охотников, рыболовов и собирателей плодов природы, необходимых для выживания. По разным оценкам около 100 000 назад человек имел примитивные орудия труда [4]. Поселения, как место постоянного проживания, возникли около 50 000 лет назад [3]. Наступившее около 30 000 лет назад похолодание затормозило культурное и экономическое развитие сообщества людей. Тысячелетнее давление внешней среды и внутренние противоречия в социуме в послеледниковый период подвели человеку к созданию аграрного сообщества, которое стало быстро формироваться около 10 000 лет назад. В основе общества лежало разведение скота и выращивание зерновых культур. Постепенно шло и развитие ремесел, обеспечивающих аграриев и животноводов необходимыми для производства продукции изделиями, инструментами и орудиями труда. По мере роста населения происходило и расширение производства за счет внутренних ресурсов и освоения новых территорий. Развивающаяся экономическая система на каком-то этапе потребовала организации системы управления. Возникшая около 6 000 лет назад письменность привела к созданию системы обучения подготовки специалистов-управленцев для всех уровней аграрного общества [5]. С организацией в XVI веке промышленного производства начинается процесс создания на базе аграрного общества индустриального сообщества.
Рост народонаселения определяет и развитие сообщества людей, его уровень культурного и экономического развития не только на ближайшее время, но и в далеком будущем. Устойчивое уменьшение численности населения страны является одним из первых признаков начала ее гибели. Этот признак определяет и начало распада или гибели любых объединений людей: культурных, этнических, общественных [1].
Модели динамики численности населения мира
Одним из первых, кто обратил внимание на закономерности роста народонаселения, был Мальтус. В его исследовании было установлено, что численность населении растет в геометрической прогрессии [6]. То есть годовой прирост населения пропорционален численности населения. В рамках аппарата дифференциальных уравнений математическая модель динамики населения имеет вид [7–8]:
dN
— = uN dt
, где N
—
численность населения, ^
—
удельная скорость роста численности
населения, определяемая как разность между рождаемостью и смертностью. Параметр ^ — зависит от репродуктивного возраста женской особи, времени вынашивания плода, возрастной структуры смертности населения. Для двуполой популяции может принимать разные значения, но не может быть больше ½. Этот параметр изменяется во времени, поскольку изменяются культурная и экономическая составляющие общества. Например, в России в XIX веке удельная скорость роста была около 0,02, а во второй половине XX опустилась до 0,005.
В середине XX века экономисты предложили описывать рост численности населения мира функцией [2]:
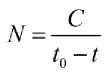
В этом случае динамическая модель представляет собой дифференциальное уравнение:
dN dt
А это означает, что прирост численности населения пропорционален квадрату численности. То есть у каждого нового поколения рождаемость у каждой пары особей должна увеличиваться в геометрической прогрессии. То есть, если, например, у первого поколения было двое детей, то их дети должны принести четверых детей, их внуки — 16, правнуки — 64. Это не согласуется с количественными изменениями численности любой популяции. Поэтому уравнение (2) можно использовать, в лучшем случае, для описания роста населения на отдельных временных интервалах для аппроксимации статистических данных.
Учет численности населения отдельных стран и регионов происходил в глубокой древности. Однако статистические данные о переписях III–I тысячелетий до н. э. до нас не дошли. Отдельные фрагменты известны из данных цензов, проводившихся в Римской империи [2]. В средние века при регистрации родивших детей делались записи в церковных книгах. По этим архивным данным можно оценить динамику численности населения отдельных городов на отдельных временных промежутках. Последующая аппроксимации полученных данных на более обширные территории позволяет оценить и численность населения страны. Однако точность таких данных будет не очень высокой. Полные переписи населения отдельных стран стали проводиться только во второй половине XVIII века. В России такая первая перепись была проведена в конце XIX века, а в странах Азии начало полным переписям было положено уже в XX веке. Поэтому численность населения мира с I по XIX вв. носит оценочный характер, и чем дальше в глубину веков, тем ниже точность статистических данных.
Математическая трактовка гиперболического роста населения (1) приводит к бесконечно большой численности населения к моменту времени t0. Но это невозможно в силу ограниченности ресурсов, обеспечивающих жизнедеятельность человека. В аргументированной концепции гиперболического роста населения мира, разработанной С. П. Капицей [9], уравнение (2) используется как вариант описания «демографического взрыва». Но в рамках подходов, используемых при моделировании взаимодействующих популяций [7–8, 10], рост численности населения более высокими темпами в доиндустриальный период, чем предсказывает модель (2), можно описать, учитывая его экономическую деятельность.
Модель общества охотников-собирателей
Общество охотников и собирателей основывалось на использовании готовых продуктов питания и простейших орудий труда, взятых у природы. По мере роста численности населения увеличение количества необходимых ресурсов происходило за счет незначительного расширения территории для охоты и сбора плодов. В этих условиях территория проживания с ограниченными ресурсами могла обеспечить выживание ограниченному количеству участников сообщества. Поскольку конкуренты в среде обитания человека отсутствовали, то модель такого сообщества можно представить моделью одиночной популяции с лимитированным ростом [7–8]:
S.+bN
-N/K.
где + On — доступные природные ресурсы, которые могут обеспечить увеличение численности населения, а на непосредственное увеличение численности населения расходуется S* — ресурсов; K* — максимально возможная емкость среды, данная от природы, (максимальная численность населения, которое может проживать на ресурсах среды в экологической нише ограниченного в пространстве размера); Un — удельная скорость роста численности населения при изобилии ресурсов (при S* ).
Из уравнения (3) следует, что без освоения новых ресурсов максимальная численность населения подсчитывается по формуле
' S.+bN
Формирование социальных объединений людей произошло, по-видимому, как естественный ответ на внешние угрозы существованию человека. Коллективное преобразование окружающей среды сопровождалось и изменением самого человека [4, 11]. Накапливаемые тысячи лет опыт и знания привели к осознанию и умению создавать собственный продукт для обеспечения жизнедеятельности — выращивать урожай и разводить скот [4].
Примем, что население общества охотников-собирателей постепенно стало производить продукт S . Максимально возможное количество этого продукта, которое можно произвести при существующих технологиях его производства равно S∞ . Примем, что скорость роста численности населения и скорость роста продукта описывается системой уравнений:
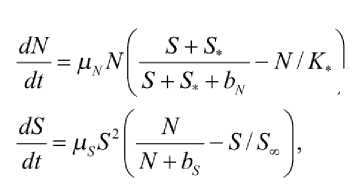
где ^s — параметр, характеризующий скорость роста произведенного продукта. Предполагается, что при малых значениях S — скорость его роста пропорциональна S2 , поскольку на начальном этапе ресурс расходуется на само воспроизводство. N / N +bs — доля трудовых ресурсов, участвующих в воспроизводстве этого ресурса. S∞ — объем максимального совокупного продукта, который может быть произведен при существующих технологиях его производства.
В модели (4) численность населения в стационарной точке будет лежать в диапазоне
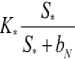
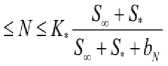
Максимальная численность населения K* достигается при ® . То есть при полном освоении среды обитания численность населения не превысит значение K*.
Модель аграрного общества
В аграрном обществе осваивались новые территории для выращивания урожая, выращивались новые культуры, производилась селекция домашних животных. Одновременно с этим происходило и освоение новых территорий, как мирным путем, так и военным. Вопрос о времени начала вооруженных конфликтов остается открытым [12]. Но в начальный период формирования аграрного общества государства уже имели армии для защиты своей территории и завоевания территорий сопредельных государств [13]. Победы в вооруженных конфликтах одерживали, как правило, страны с более развитой экономикой. То есть, на завоеванные территории приносились более современные методы ведения хозяйства. Поэтому военный фактор рассматривается как вариант увеличения ресурса .
Примем, что население осваивает и новые трофические ресурсы (территории), динамика изменения которых описывается уравнением:
dt K \N + bK \ Л
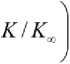
где №k — параметр, характеризующий скорость роста «производственных площадей». Предполагается, что при малых значениях K — скорость роста пропорциональна K2 , поскольку на начальном этапе освоенный новый ресурс расходуется на само воспроизводство, а осваивается медленно. N / N + b K — доля трудовых ресурсов, участвующих в воспроизводстве этого ресурса. K∞ — объем максимального совокупного продукта, который может быть произведен при существующих технологиях его производства.
С учетом (4)–(5) модель динамики численности населения принимает вид:
dN ( S + S, N ] (6)
dt \^S + S, + bN К + К, J dt + M’ dK ( N К У dt {^ + bx
При S = 0 модель (6) рассматривается как модель общества охотников-собирателей, расширяющих территорию своего обитания. Система уравнений (6) имеет тривиальную стационарную точку : N = 0, S = 0, K = 0.
В этой точке матрица Якоби правой части системы уравнений (6) имеет одно положительное собственное значение:
и два равных нулю. Это обеспечивает рост функции N(t). Тогда при достаточно больших значениях N сколь угодно малое возмущение функции S и K , как это следует из второго и третьего уравнений в (6), приведет к их росту. Это согласуется с данными исторического процесса роста численности населения мира — период существования общества охотников-собирателей длился несколько десятков тысяч лет, прежде чем было положено начало сельскому хозяйству.
Нетривиальная стационарная точка системы уравнений (6) находится из решения системы алгебраических уравнений:
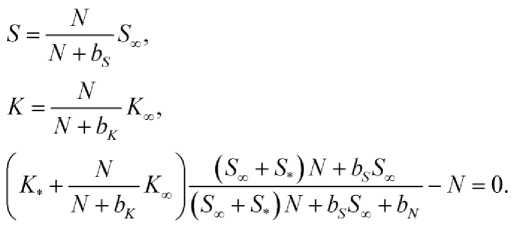
Левая часть третьего уравнения в (7) при N = 0 принимает положительное значение, а при N = K * + K∞ — отрицательное. Поэтому эта система уравнений имеет хотя бы один положительный корень.
Освоение новых территорий требует организации управления. То есть часть населения становится управленцами. Управление позволяет ускорить производство продукции S и освоить новые территории K . При этом в реальном аграрном обществе управленцы постепенно стали превращаться в крупных землевладельцев, присваивая себе часть территорий. В этом случае модель представлена системой уравнений:
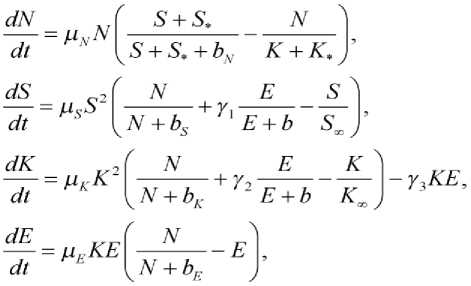
где E — доля населения, участвующая в управлении, /1 , /2 , /з , , ^Е , ^Е параметры, характеризующие скорости процессов.
В четвертом уравнении в (8) слагаемое N / N + bE — доля населения, участвующая в организации производства и в освоении новых территорий. Поскольку аграрное общество консервативно, то считается, что система управления мало изменяемая, технологии управления не стареют.
у KE
Слагаемое в (8) скорость «изъятия» территорий управленцами для собственных нужд. Пропорциональность этой скорости первым степеням K и E означает возможность «изъятия» управленцами всех новых ресурсов. В реальном эволюционном процессе аграрного общества это согласуется с возникновением крупных землевладельцев.
Е
Слагаемое £ во втором уравнении в (8) вклад управленцев в создание продукта
Е
S , а слагаемое к + п в четвертом уравнении вклад в создание новых площадей. Локальная скорость роста численности управленцев пропорциональна Не . То есть скорость роста числа управленцев тем больше, чем больше «емкость» новой среды.
Модель реконструкции численности населения мира
Численность население мира оценивается на 10 000 год до н. э. от 1 до 10 млн человек. Если считать, что первое организованное сообщество людей имело около 1000 человек и за 100 000 лет выросло до 10 млн [2], то скорость роста общества охотников-собирателей оценивается в 0,0001–0,0002 1/ год. К 1 году н. э. численность населения мира составляла около 150–300 млн [2, 14]. С учетом этого скорость роста была около 0,0005 1/ год. Социальное общество начала нашей эры состояло из небольшого числа богатых людей, свободных граждан и рабов. Весь произведенный продукт распределялся неравномерно. Если считать, что основной массе свободных граждан и рабов доставалась 1/10 общего продукта, то удельная скорость роста численности населения ^N была около 0,005.
Темпы освоения новых территорий можно сопоставить с темпами роста числа войн. Из данных Т. Харботла [15] следует, что за 500 лет, начиная с VI века до н. э. и до I века н. э., их количество увеличивалось в 20 раз (оценочное значение). Это соответствует значениям параметров P'S и Рк в 5–10 раз больше, чем значение параметра Pn .
В системе уравнений (8) можно принять, что S * = 1 и K * = 1. Тогда система уравнений (8) будет описывать динамику не абсолютных значений N(t), S(t) и K(t) , а их изменений относительно S*(N(t) и S(t) и K * (K(t)). С учетом этого в (8) приняты следующие значения параметров:
5. = 1,^.= 1,^=2, ^=4,
HN = 0.0038, ns = 0.02, Lt . = 0.04, nh; = 0.6, bN = 2, bs = 1, bK =2,b = 2, b,; = 20, /, =15,/2=45,y3 = 0.5.
Основные результаты моделирования приведены на Рисунках 1–3. За начало отсчета принят 1 г. н. э. На Рисунке 1 приведено изменение численности населения мира (статистические данные отмечены символом «*»), изменение числа вооруженных конфликтов (учтено 835 войн, статистические данные отмечены символом «о»), расчетные зависимости (пунктирная линии). Одна из расчетных зависимостей, полученная при условии, что в (8) E = 0 , отмечена как «без управления». Как следует из полученных результатов, модель объясняет увеличение численности населения мира к 1700 году по сравнению с 1 г. н. э. в четыре раза. По статистическим данным Э. Мэддисона [14] этот показатель равен 3.
На Рисунке 2 приведены зависимости S(t) и K(t) . Пунктирные линии соответствуют решению системы уравнений (8) при условии, что E = 0. Как следует из полученных результатов на заметное влияние «управленцев» на рост S(t) и K(t) уходит около 1/3 моделируемого периода. Наличие «управления», как следует из анализа полученных результатов, увеличивает темпы роста и населения (Рисунок 1) и ресурсов S и K (Рисунок 2).
Моделирование «альтернативных» вариантов роста численности населения осуществлялось следующим образом. На эволюционной процесс роста численности населения мира накладывалось множество случайных событий: эпидемии, катастрофы, внутренние противоречия, вызвавшие многочисленные людские потери. В рамках модели (8) принимается, что на 1 г. н. э. параметры этой системы могли отличаться на 50% от параметров (9). При этом предположении осуществлялось решение уравнений (8) для 50 000 вариантов параметров, выбранных случайным образом. Результаты моделирования приведены на Рисунке 3. Как следует из анализа полученных результатов среднее значение роста численности населения — увеличение за 1700 лет в 4 раза. Вместе с этим темпы роста численности населения могли быть и более высокими (Рисунок 3).
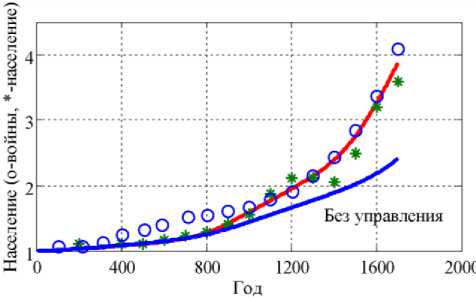
Рисунок 1. Прирост
(пунктирные линии), населения мировых войн (о) .
населения мира (*),
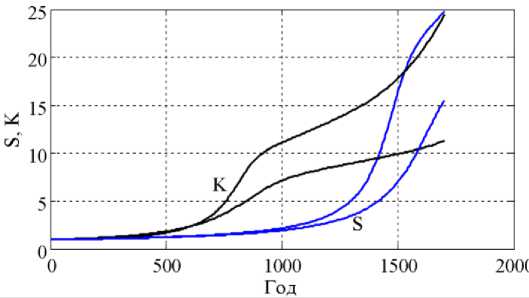
Рисунок 2. Прирост и за 1700 лет по сравнению с 1 г. Пунктирные линии соответствуют зависимостям в отсутствие управления .
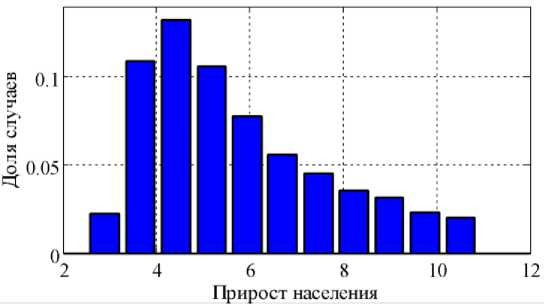
Рисунок 3. Прирост населения к 1700 г. (альтернативные варианты).
Заключение
Численность населения регионов и стран мира от доисторических времен до начала индустриального периода оценена исследователями с немалой погрешностью. На жизнь людей накладывались различные внешние и внутренние причины, приводившие к большим человеческим жертвам. Тем не менее, в целом, рост численности населения мира происходил быстрее, чем в предполагаемой геометрической прогрессии. Это можно объяснить уходом сообщества людей из зоны борьбы за выживание за счет создания и последующего расширения собственных источников существования.
Список литературы Математическая модель аграрного сообщества
- Тойнби А. Д. Исследование истории: Возникновение, рост и распад цивилизаций. М.: АСТ МОСКВА, 2009. 670 с.
- Малков А. С., Малинецкий Г. Г., Чернавский Д. С. Моделирование развития аграрных сообществ с позиций нелинейной динамики. Новое в синергетике. Новая реальность, новые проблемы, новое поколение. М.: Наука, 2007. 383 с.
- Grinin L., Grinin A., Korotayev A. A quantitative analysis of worldwide long-term technology growth: From 40,000 BCE to the early 22nd century // Technological Forecasting and Social Change. 2020. P. 119955. DOI: 10.1016/j.techfore.2020.119955
- Вишняцкий Л. Б. Человек в лабиринте эволюции. М.: Весь мир, 2004. 152 с.
- Коротаев А. В., Халтурина Д. А., Божевольнов Ю. В. Законы истории: Вековые циклы и тысячелетние тренды. Демография, экономика, войны. М.: Издательство ЛКИ, 2010. 256 с.
- Мальтус Т. Р. Опыт закона о народонаселении. М.: К. Т. Солдатенков, 1895. 251 с.
- Колпак Е. П., Ефремова А. Е. Математические модели одиночной популяции. Казань, 2017. 122 с.
- Murray J. D. Mathematical biology: I. An introduction. Springer Science & Business Media, 2007. V. 17.
- Капица С. П. Математическая модель роста населения мира // Математическое моделирование. 1992. №4.6. С. 65-79.
- Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск, 2003. 368 с.
- Крылов А. К., Марков А. В., Александров Ю. И. Единство популяции как способ выживания в нестабильной среде // Журнал общей биологии. 2020. Т. 81. №3. С. 194-207.
- DOI: 10.31857/S0044459620030057
- Вишняцкий Л. Б. Война до истории // Человек. 2016. №6. С. 59-74.
- Аль-Убейди Ш. М. И. Шумерская и аккадская армии в древнем Ираке: сравнительно-исторический анализ // Вестник ВГУ. Серия: История. Политология. Социология. 2012. №2. С. 70-74.
- Мэддисон Э. Контуры мировой экономики в 1-2030 гг. Очерки истории. М.: Изд. Института Гайдара, 2012. 584 с.
- Харботл Т. Битвы мировой истории. М., 1993. 576 с.


