Математическая модель алгоритмов пеленгования источников радиоизлучения фазо-корреляционными пеленгаторами с пространственным распределением элементов пеленгационной решетки

Цифровые технологии обработки СВЧ-радиосигналов позволяют реализовать пеленгацию источника радиоизлучения (ИРИ) в широком частотном диапазоне при произвольном расположении элементов пеленгационной антенной решетки в пространстве. Это упрощает размещение таких пеленгаторов на малоразмерных объектах (самолеты, дистанционно пилотируемые летательные аппараты, ракеты и т. д.) и создает предпосылки для повышения качества их функционирования.

Вместе с тем при проектировании таких пеленгаторов возникают трудности при исследовании алгоритмов пеленгования из-за отсутствия математических моделей в виде совокупности расчётных соотношений, описывающих процесс пеленгации с учетом произвольного расположения элементов пеленгационной решетки и наличия неидентичностей каналов и внутренних шумов приемного тракта.

В настоящей статье приводится описание одного из вариантов математической модели процесса пеленгования ИРИ.

В пространстве выбрана заданная система декартовых координат ZXYс началом в точке O (z=0, x=0, y=0).

В пространстве действует ИРИ на длине волны λ. ИРИ расположен в точке М u (z=z u , x=x u , y=y u ).

Существует пеленгационная система в виде фазо-корреляционного пеленгатора с произвольным расположением элементов пеленгационной решетки. Она включает в себя [1]:

• -    опорную антенну, находящуюся в точке М оп (z=z оп ,x=x оп ,y=y оп ) . Диаграмма направленности опорной антенны равномерна в секторе нахождения ИРИ;2

• -    пеленгационные измерительные антенны – N антенн в точках М₁, М₂, М₃,… М_N – M_i(z=z_i,x=x i ,y=y_i) i = 1,N. Диаграммы пеленгационных антенн подобны диаграммам направленно-

• Карманов Юрий Трофимович – д-р техн. наук, профессор кафедры инфокоммуникационных технологий, Южно-Уральский государственный университет; ea@drts.susu.ac.ru

сти опорной антенны - равномерные в секторе нахождения ИРИ;

• -    пеленгационную систему, которая в процессе пеленгации ИРИ проводит измерение фазовых сдвигов между радиосигналами, принимаемыми i- й пеленгационной антенной и опорной антенной - Ф_;(0_и,Р_и), i = 1, N, зависящие от азимута 0_и и угла места e u ИРИ;

• -    измеренные значения фазовых сдвигов ф_;(0_и, Р и ), по которым в пеленгационной системе вычисляются значения Дфу = ф_; — ф j , i <  j, i = 1,N, которые используется в пеленгационной системе для оценки значений - (0_и, Р и );

• -    пеленгационную систему, предварительно тестируемую, путем измерения фазовых сдвигов между радиосигналами от i- й антенны и опорной антенны фп^^к), в Т (к), Л Т л)), принимаемых тестовых ИРИ (ТИРИ), находящихся на тестовых углах 0 т (к), в т (к), к = 1,М и излучающих последовательность радиосигналов с длинами волн Л т (п), п = 1,L_T. На основе тестовых значений ф1Т (0 Т (к), вТ^к), ЛТ^.п)') вычисляется массив значений А т ф у (0 Т (к), в Т (к), Л Т (п)) = фi П Т0 T Тk), №), Л-^ -ф П 0 Т (к), в Т (к), Л Т (п)) j = 1,N, i = 1,j, к=1,М, п = 1,L_T. Тестовый массив хранится в базе данных пеленгационной системы и используется при вычислении пеленга ИРИ фазо-корреляционным алгоритмом.

Фазо-корреляционный алгоритм пеленгации ИРИ , который заключается [1 ]

• а)    в измерении ф(0 и , в и , Л), i = 1,N и вычисления по ним Дф , (0 и , в и , Л) = ф , (0 и , в и , Л) - ф , (0 и . в и , Л) , i

• б)    вычислении корреляционной суммы 1(0 т (к), в Т (к), Л Т (п)/ 0 и , в и , Л), где Л Т л) - тестовое значение длин волн ТИРИ ближайщее к длине волны Л пеленгуемого ИРИ (определяются по результатам измерения несущей частоты пеленгуемого сигнала) по выражению (1):

  г

  
  

  ,Ри.^ =

  
  

1(0_т(к'),Р т (к'),^^(П ^ )

\             0и

N(N — 1)

/

j=1 \К]

у cosS tj

/

й у² ^SiLTlStj /

Uj = Дф/j(0u,Рu,Я)—ДтФij(0т(k),Рт(k),Л(nЛ));

(1) в) вычислении пеленгационного сигнала

Т(0 Т (к), в Т к), Л Пп/^_и, в и , Л ) =

= -1О1д(/(0т(к), вТк), Лт(л)/0и, ви, Л)),

Л т (л л ) - значение Л т (л л ), п = 1,L_T ближайшее к длине волны ИРИ - Л ;

• г)    в качестве оценки пеленга ИРИ 0 и , в и выбираются значения 0_и = 0_т(к_о), Р_и = в_т(к₀), при которых пеленгационный сигнал Т (0 _т ( к ), вТ^к), Л т (п)/0 и , в и , Л) достигает своего абсолютного минимума,

Т\0 и = 0 т (к о ),Р и = в т (к о )\ =

= Мт_к=^Т(0 т (к), Р т (к), А т (п_х)/0 и , Р и , А)

Процессу пеленгования мешают следующие факторы:

• -    наличие шумов в измерительных радиоканалах пеленгатора;

• -    неидентичности фазовых характеристик антенн, каналов пеленгатора.

Все эти факторы приводят к появлению в измеряемых значениях ф ; паразитных фазовых сдвигов - E i , значения которых не связаны с измеряемыми пеленгами.

В математической модели будем полагать, что E 1 , e₂,.. E N - случайные величины.

Задача состоит в нахождении совокупности математических выражений, позволяющих вычислить пеленгационный сигнал Т^Т^к), вТ^к), Л т ( л )/0 и , в и , Л) по заданным характеристикам пеленгационной системы и заданным значениям E 1 , E 2 ,. E n , в сферической и угловой системах координат.

Математическая модель алгоритмов пеленгации в сферической системе координат В задачах радиолокации и радионавигации используется сферическая система координат, изображенная на рис. 1.

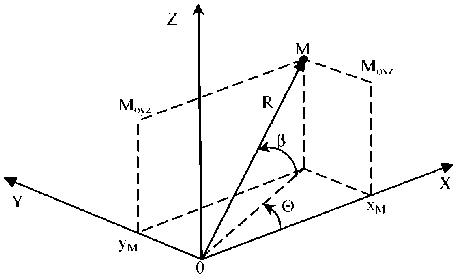
Рис. 1. Сферическая система координат

Координаты точек в сферической системе R, 0 , в связаны с декартовыми координатами соотношениями:

1 х = R • cosP • cos0, у = R • cosP • sin0, z = R • sinp.

Фазовый сдвиг между радиосигналами ИРИ, принятыми i -й антенной и опорной антенной, вычисляется в сферической системе координат по выражению:

Математическая модель алгоритмов пеленгования источников радиоизлучения фазо-корреляционными пеленгаторами с пространственным распределением элементов…

Г         ф₁ (д и , Р и , Л)   2v ^: 5 + _Е . ,

1 ^ф /Т ⁽6 т ^(к), ^ Т ^(к)^,Л Т ^(п я )) = 27 ^ _г °" + ^£ Т1, X                                         Л г ⁽ п ^ )

где R i , R on – расстояние между ИРИ и i- й измерительной и опорной антеннами.

Значения R i , R on вычисляются по выражениям:

Г ^ = ^[(x_z^- %J² + ⁽y ^- yj² + ⁽z_t ^- z_u^)2]1 / ², t^ on = ^[(^ on ^— ^ u ) ⁺ (N on У и ) ^{+ (}^ on ^— ^ u ) ^] ■

Заменяя в данном выражении декартовые ординаты на сферические, запишем значения меряемых ф ^ и тестовых ф^:

Ф ( 0 „ , ^р _и , z ) — [ x i cos ^р _и cos © и ⁺

• + У 1 sin Р и cos © и + ^z i sin Р и ] + ^E i ,

Фиг ( ©T (k), рг ( k) , У (пЯ)) -

• - —-—- x_iT cos P _t ( k ) cos © _T ( k ) ,

  ко-

  из-

  
  

ф2Г (©T (k) , рг ( k) , У ( пЯ )) -

2 „

• ^-—--- У г sin ^p T ( ^k ) cos © t ( ^k )

Фы г ( © т ^{( k )} , ^р г ^{( k )} , ^/ Г ^{( п} Я ⁾ ) ^- ^ , 27 х z i sin P t ( ^k ) ^,

Математическая модель алгоритмов пеленгации в угловой системе координат

Угловая система координат используется в задачах радиоуправления летательными аппаратами. Положение точки М в угловой системе координат характеризуется координатами:

• •    R - расстояние от начала координат до точки М;

• •    а_х - горизонтальный угол линии визирования ОМ в плоскости ZOX;

• •    а_у - вертикальный угол линии визирования ОМ в плоскости ZOY.

Угловая система координат представлена на рис. 2.

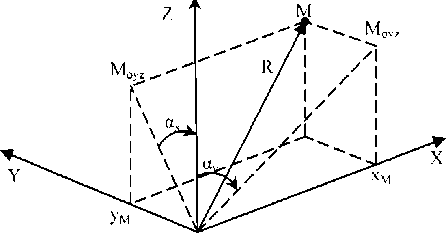
Рис. 2. Угловая система координат

Сферические координаты точки М связаны с угловыми координатами соотношениями:

фг (©т (k), Pt (k), Яг (пЯ)) ~

^- Фи г ⁺ ^ 2 iT ⁺ Ф з гг ^{+ E} Ti ,

tg © ^-

tg «У tg «X

E Ti - случайные ошибки измерения тестовых фа

|sin р - ^[ 1 + tg² « х + tg² « у ] ^1/2

зовых сдвигов ф_1Т .

Используя выражения (1) и (3), представим выражения для пеленгационного сигнала в сферической системе координат в виде:

⁵ а ^- 2 7 [ ⁽ x i "  x j ) cos ^р и cos ©^{u +}

+ (yi - У;)cos ри sin ©u ++ (zi - zj )sin ри + (Ei - Ej )] -

Используя эти соотношения, представим выражения для пеленгационного сигнала в угловой системе координат в виде:

s 2.7 ^i - — i Я

^(x i ^{- x} j )tg « x ⁺ ( y i ^- У ; )tg « y ^{+ (z} i

-

27 , [ ( x i - X ; ) cos ©_T ( k ) cos P _t ( k ) +

2 7 -----X ^{Я (п} Я )

^j +

<

+ ( y i - У ; ) sin P _t ( k ) cos ©_T ( k ) + ^{+ ( z} i ^{- z} j ) ^{sin р} г ( ^k ) ^{+ ( E} Ti ^{- E} Tj ) ] , T ( © t ( k ) , P t ( k ) , Я г ( n _x ) / © и , Р и , Я ) -

= - 10lg ^

N

Z cos ⁸ i

A ²

A ²

^(x i ^- x ; ^)t g « Tx ( ^k ) ^{+ (} y i ^- У ; tg « Ty ^{( k ) + (z} i ^{- z} j )

1/2

^{+ ( E} Ti    ^E Tj ) ] ,                                             ⁽⁵⁾

^T [Tx ( ^k ) , « Ty ( ^k ) , ^Я Т ( ^п Я ) / « х , « y , ^Я ] ^-

N

+ ^ sin ⁸ i

,

= - 10lg ^

г

N

У cos ⁵ i

А2

г

N

⁺ Z sin 8 ij

А2

г ,

Я _Т ( п я ) - значение Я _г ( п ) , ближайшее к Я .

V i <  ^;

R ^ ^ ; « _x , « y - угловые координаты ИРИ

|a _x | <  90° , | a _y | < 90 ° ; a _Tx , a _Ty - угловые координаты тестового ИРИ | a _Tx | <  90 ° , | a Ty | <  90 ° .

Предложенные математические модели удобно использовать при выборе параметров пеленгаторов путем оперативного моделирования их пеленгационных характеристик для исключения ложных пеленгов, формирования требований к неидентичностям каналов пеленгатора и уровням шумов в них.

В качестве примера, иллюстрирующего сказанное, на рис. 3 приведена пеленгационная характеристика пеленгатора, у которого пеленгационные элементы расположены по спирали на стенках цилиндра диаметром и высотой 30 см, при пеленгации ИРИ с 0и = 20°, ^м = 45° и X = 30 см. Ось цилиндра совпадает с осью OZ.

Как следует из рисунка, пеленгатор с такой «экзотической» пеленгационной антенной решеткой имеет пеленгационную характеристику с ярко выраженным минимумом в направлении ИРИ.

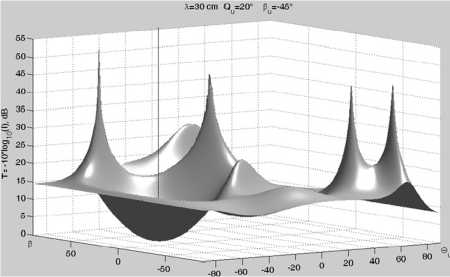
Рис. 3. Пеленгационная характеристика

Ложные минимумы на 10 дБ меньше истинного минимума, что позволяет прогнозировать низкий уровень появления ложных пеленгов.