Математическая модель антропогенного воздействия на популяцию

Добыча полезных ископаемых и их промышленная переработка сопровождаются выбросами в окружающую среду различных элементов и их химических соединений. Вредные для всего живого вещества антропогенного происхождения, такие как окислы серы, соединения азота, металлическая пыль, тяжелые металлы, наполняют воздушный и водный бассейны, загрязняя обширные территории [1]. Загрязнение ведет к кардинальным изменениям условий существования населяющих эти территории растений и животных, может изменить направленность и формы естественного отбора и генетическую структуру природных популяций, привести к уменьшению видового разнообразия и исчезновению отдельных видов.

Мощными источниками загрязнения являются крупные центры горнодобывающей и горно-перерабатывающей промышленности [2]. Выбрасываемые в атмосферу и водные системы токсичные вещества распространяются на десятки километров от источника, накапливаются в почве, в воде, в донных отложениях. По различным трофическим цепям попадают в организмы животных и растений и накапливаются в них [3].

Загрязнение среды обитания. По радиусу от источника загрязнения выделяются три зоны: импактная, буферная и фо- новая. Наиболее загрязненной является импактная зона, значительная часть которой представляет собой техногенную пустошь. Накопление поллютантов происходит и в буферной зоне, но степень загрязнения не является основной причиной гибели всего живого в этой зоне. В фоновой зоне принимается, что накопление поллютантов незначительно [4]. Размер импакт-ной зоны, зависит от степени поражения территории поллютантами. Наибольшая их концентрация может быть не непосредственно вблизи источника, а на некотором удалении от него. Накопление токсикантов растительностью от точки максимума концентрации поллютантов в импактной зоне зависит от расстояния от этой точки и убывает в первом приближении по экспоненциальной зависимости по градиенту концентрации [5].

Биодоступность различных элементов, находящихся в окружающей среде зависит от условий среды, которые влияют на форму существования данного элемента или его химического соединения; токсичности элементов и их способности к комплексообразованию; уязвимости организма-реципиента [6, 7]. В эволюционном процессе живого вещества сложилось равновесное соотношение между естественной концентрацией веществ во внешней среде и в организме. При превышении концентрации микроэлементов в окружающей среде порогового значения, которое зависит от множества геохимических факторов, внешний «избыток» веществ разными путями может поступать в живой организм и накапливаться в нем [7, 8].

Накопление токсичных веществ происходит в тех структурах организма, которые лимитируют процессы метаболизма и биосинтеза. Поглощенные организмом, они могут мимикрировать под элементы, необходимые для нормальной жизнедеятельности организма, вызывая нарушение многих биохимических функций в клетках. Это приводит к тяжелым поражениям жизненно важных органов и нервной системы отрицательно влияет на наследственность. Вместе с этим происходит и детоксикация элементов за счет имеющихся в организме белков или за счет синтеза соединений, нейтрализующих токсиканты в организме. Работает также и механизм, направленный на снижение потенциальной токсичности элементов путем ограничения активности элементов во внутриклеточных образованиях [6].

Импактная зона. Модель одиночной популяции в импактной зоне. Математическая модель одиночной популяции с ограниченным ростом имеет вид [9, 10, 11]

dN dt

= ^ N ( 1 - N / K )

, (1)

где Р - удельная скорость роста популяции, определяемая как разность между рождаемостью и смертностью особей, а K - емкость среды обитания (равновесное количество особей, которое может существовать в экологической нише популяции).

В процессе эволюции живого вещества рождаемость и смертность особей в популяции медленно изменялись в течение тысячелетий под влиянием внешних и внутренних факторов. На временных интервалах длиною несколько столетий их можно считать неизменными. В условиях антропогенного давления на популяцию накопление организмом тяжелых металлов и их соединений в больших количествах может изменить внутренний метаболизм организмов особей в течение 2-3 поколений. В результате может измениться плодовитость особей, время вынашивания плода, различные физические характеристики особей [12].

Как показывает анализ результатов полевых наблюдений токсиканты ( P ) накапливаются в организме, живущем на загрязненной территории, до некоторого порогового значения индивидуального для каждого организма [13]. Особи, накопившие значительные количества токсичных веществ могут погибнуть, а у части популяции накопление токсичных элементов может быть и незначительным. При этом, если популяция не погибает, изменяется ее удельная скорость роста. Вместе с этим загрязнение территории сопровождается уменьшением занимаемых особями площадей и уменьшением трофического ресурса. То есть уменьшается емкость среды (экологической ниши). Антропогенное давление может оказывать влияние на всю популяцию в целом, вынуждая часть особей мигрировать из импактной зоны в буферную, а из буферной в фоновую.

Пусть удельная скорость роста в им-пактной зоне при наличии токсикантов в

P количестве I изменяется на величину

1 + ар

1 + ар

,

размер ниши на величину

1 + b Pi

1 + ьр а мигрируют из ферную зону импактной зоны в

бу-

N I

с Р

c1 I

1 + ср

(4) особей.

aabbcc

В (2)-(4)   1,   2,  1,  2,  1,  2 положи-

N тельные параметры, I - численность

K особей в импактной зоне, 1 емкость экологической ниши, занимаемой популяцией в импактной зоне.

С учетом этих предположений модель одиночной популяции (1) в импактной зоне принимает вид

должны c1 < c 2

удовлетворять

неравенству

К уравнению (5) необходимо добавить

изменение количества загрязнителей в

среде

P ( t )

как функцию времени. Одним

из вариантов является функция

dN, „ ( 1 + a.P, N, 1 + bP, ) ,, c.P, = N ,u I L- I- - N, L- I— dt        I 1 + a₂P K, 1 + b_xP, J     I 1 + c₂P,

.

P = 0

При I     (токсиканты отсутствуют)

эта модель переходит в модель (1). Удельная скорость роста популяции в зависимо-P сти от значения I при выполнении неравенства a1 < a2 уменьшается, но не может уменьшиться более чем на величину ua. / a,  ~

1  2. Этим учитывается факт ограни ченного накопления токсикантов организмами особей популяции и неоднородность накопления внутри самой популяции [12].

Загрязнители среды могут уничтожить часть трофического ресурса или сделать его недоступным для популяции. Размер

К <  К ниши при выполнении неравенства ^{1    2}

с увеличением количества загрязнителей будет уменьшаться. В (3) предполагается, что емкость загрязненной среды не может быть меньше K^ ^2. Этим учитывается то обстоятельство, что небольшая часть популяции может выдержать антропогенную нагрузку в импактной зоне.

В «чистой» среде происходит естественная миграция особей популяции из зоны в зону, постепенно наступает равнове-

P = 0

сие. Поэтому в (5) при 1     миграцией пренебрегается. При наличии поллютантов в среде часть особей популяции может мигрировать в поисках зоны с меньшей концентраций загрязнителей, то есть из импактной зоны в буферную зону. Поскольку мигрирует только часть популя-

^{P (} t ) = P ^{( 1} - e ^- " ) , (6)

где ^Y положительный параметр, характеризующий скорость накопления поллютантов в среде.

Эта зависимость отражает факт начала поступления загрязнителей в среду с возникновением источника загрязнения в момент времени t = ⁰ и последующего постепенного увеличения мощности источ-

P ника до значения I . В этом случае в качестве начального условия для численности популяции естественно принять N = K

^II , полагая, что на момент начала антропогенного давления на популяцию ее численность достигла равновесного состояния.

Естественное удаление загрязнителей из среды за счет их растворения, выветривания, распада и других физикохимических процессов может длиться от несколько столетий до нескольких тысячелетий [14]. Процесс достижения максимального антропогенного давления длиться от нескольких лет до нескольких десятилетий. С учетом этого стационарные состояния уравнения (5) рассматриваются как не изменяющаяся численность популяции на длительном временном интервале в условия неизменяющегося антропогенного давления.

Уравнение (5) имеет стационарную точ-

N = 0

ку ^I , которая будет устойчивой, в области отрицательных значений функции

f ( Pi) =

1 + aP

1 + a^P;

1 C 1 P i

U 1 + c₂P

ции, то значения параметров

cc

1 и 2

„ P = 0 ,       f (P)

При I    функция    I принимает положительное значение. При выполнении

неравенства 1   2 она является моно-

~  ~ кP. —— ю тонно убывающей и при I

.f ( P i ) — a- — - c ¹

a₂    ц c^

.

Поэтому

при выполнении неравенства

a

— < a 2

1 ^c

Ц С 2

f ( P )

функция     ^I может прини-

мать

отрицательные значения. В этом слу-

чае

значение

, при котором

f ( P ) = 0

7 v 7 , является пороговым значением, при превышении которого устойчивой будет тривиальная стационарная точка.

Поэтому выполнение неравенства I * в рамках модели интерпретируется как степень загрязнения экологической ниши не допускающая выживаемость популяции.

Нетривиальная стационарная точка уравнения (5)

NL = i + b i PL f ( p ) K 1 + b₂P/   I

существует в области положительных f (P)

значений функции     I , при этом по скольку собственное значение

Буферная зона. Динамика популяции в буферной зоне уравнением dN„       f 1 + aP„ N„ 1+b,P„I _. c,P,

B = nN     L—   B   2_B. + n dt       B 1 + a,P8 K„ 1+bP 11 + c,P.

\      2 B      B       1 B y              2 I

численности описывается

—

_N c ^{1 P}B

B

^{1 + c} 2 ^PB ,(7)

N где B численность особей в буфер-

K ной зоне, B емкость буферной зоны. Последнее слагаемое в (7) – скорость миграции особей из буферной зоны в фоновую.

Количество поллютантов в буферной зоне меньше [4, 5], чем в импактной зоне. С учетом этого в (7) принимается, что есть p_R

P

^BI ( ). В дополнение к этому считается, что в буферной зоне популяция погибнуть не может, то есть должно вы-

полняться неравенство

Стационарное состояние

.

N B = 0

при

N >  0

выполнении неравенства I     не лизуется. В случае, если в импактной

N = о в стационарном состоянии I ,

реа-зоне

ста-

ционарной точкой буферной зоны является

N JL = ^{1 +} b i ^PB f ( p )

K_B  1 + bp

B        2 B

.

В силу выполнения неравенства

2 = -1NI 1 + b2 PI ц Kj 1 + bp матрицы Якоби имеет отрицательное значение, эта точка будет устойчивой.

В случае динамической задачи, когда известен закон поступления загрязнителей

P. = P, ( t )

в среду ^II , при условии, что

P ( t = 0) = о                  t = u

Iх    '    , момент времени       дос- тижения значения

является поро-

говым моментом временем, после которого начинается процесс «гибели популяции».

B * , это стационарное состояние реализуется и будет устойчивым.

Фоновая зона. Для фоновой зоны принимается, что токсиканты в ней отсутствуют, но в эту зону мигрируют особи из буферной зоны. При этих предположениях динамика численности популяции в фоновой зоне описывается уравнением dN„   f L NF I , t cP

—- = nN„ 1--- + N„ —^B— dt        (   Kp)   B1 + c2Ps   (g)

N где F численность особей в фоновой

K зоне, F емкость фоновой зоны, а сла- cANRP /(1 + cP )

гаемое 1 B B v    2 B7 скорость ми- грации особей из буферной зоны в фоновую.

Стационарная численность популяции в фоновой зоне определяется как положительный корень квадратного уравнения

• ^—- N 2 - m N — N_B c ¹ P B = 0

K f ^{F     F}     B 1 + C 2 P B

•

K

Это значение будет не меньше, чем ^F за счет миграции в фоновую зону особей их буферной зоны.

В динамической постановке задачи принимается, что в начальный момент времени во всех зонах численности популяций равновесные, а поллютанты отсутствуют

Ni (t = 0) = Ki      NB (t = 0) = KB

,                                                                                    ,

Nf (t = 0) = Kf          PB (t = 0) = 0

,                                                                                           ,

Nf (t = 0) = Kf

•

Эти условия соответствуют началу антропогенного давления на биоценоз, в который находится в равновесном состоянии.

Модель выживаемости популяций. В зонах антропогенной нагрузки население представлено многочисленными видами, которые возникали в различные геологические эпохи. Рождаемость, продолжительность жизни, реакция организмов на действие внешней среды у особей различных видов различные. Отдельные популяции конкретного вида разбросаны на загрязненной территории по экологическим нишам различного размера, имеют различную численность. То есть в рамках уравнения (5), (7), (8) каждой популяции многочисленных видов сопоставляются aab различные значения параметров ¹,   ² ,  ¹

, b2, c1, c2, — . Выбор этих параметры случайным образом из заданного диапазо- на можно интерпретировать как случайное возникновение видов в различные геологические эпохи. Набор таких параметров интерпретируется как «биоразнообразие» в зоне антропогенного давления. Поскольку эволюция популяций длилась тысячелетия, то предполагается, что к началу возникновения антропогенного давления на территории наступило равновесие внутри популяций. Тогда можно оценить возможные относительные изменения численности не взаимодействующих популяций, вызванные загрязнением среды обитания [15].

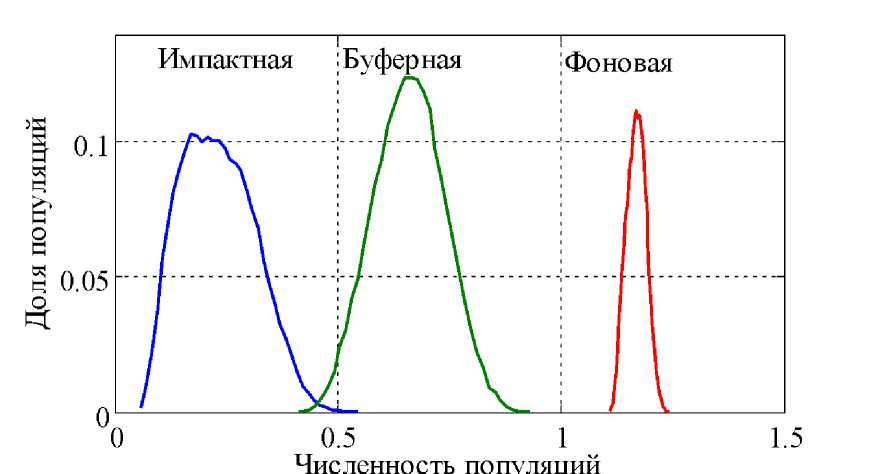
На рис. 1 приведено стационарное распределение 50 000 популяций по численности в условиях загрязнения среды обитания, для которых параметры, входящие в уравнения (5), (7) и (8), выбирались случайным образом из диапазонов: a^{1 G [}^^^], a 2 g [2,4]     b_x e [1,2]     b ₂ g [3,6] _и

,                     ,                            и c g [3,6]    c2 g[1,2]        Pi= 0.15

,                            , а                             ,

P = 0.07

B       . Этот набор параметров соот ветствует случаю отсутствия гибели хотя

P ^ 0

бы одной популяции: для любых ^I

f (P) ^ 0 n выполняется неравенство     I     . При

c выборе случайным образом параметра 1 из диапазона [1, 4]    неравенство

aA I a. < c / —c.

• ^{12   1    2} может нарушаться, что

• соответствует возможной гибели части популяций в импактной зоне в зависимости от концентрации загрязнителей (от па-P

раметра ^I ). Исходя из анализа полевых наблюдений по распределению концентрации поллютантов и оценки размеров буферной и импактной зон, приведенных в [4, 5], в работе принималось, что концентрация поллютантов в буферной в два раза меньше, чем в импактной.

Рис. 1. Распределение популяций по численности в условиях антропогенного давления в трех зонах

В динамике момент времени t  t * дос-

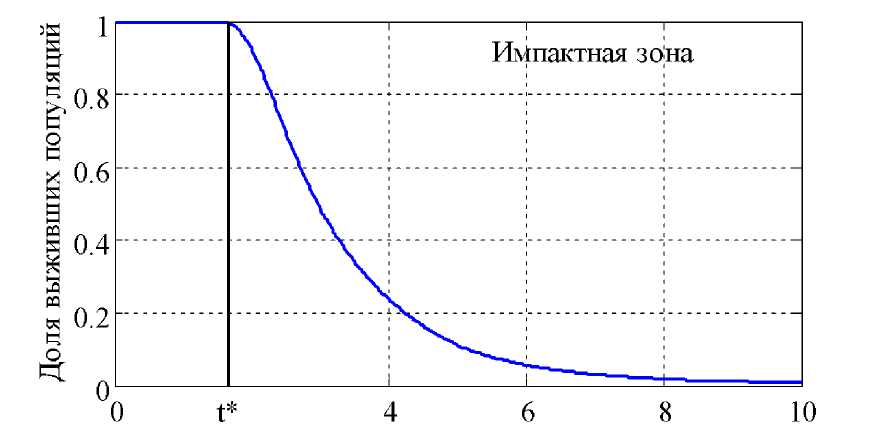
P тижения порогового значения от начала загрязнения среды зависит не только от aabbcc параметров 1,   2,  1,  2,  1,  2 , но и от удельной скорости роста популяции ^ и скорости поступления токсикантов в среду обитания. Для случая динамики поступления загрязнителей в среду по закону (6) на рис. 2 отражено изменение числа «выживших» популяций на текущий момент

п             P) = 10 Ц времени. Принималось, что 0     , а '

выбиралось случайным образом из диапазона [1,2] для 10 000 популяций. Порого- вое значение момента времени, по достижении которого начинается гибель части популяции, отмечено как t* . Влияние поллютантов на сообщества людей, проживающих на загрязненных территория, можно оценить на основе теории нечетких множеств [16].

t

Рис. 2. Доля выживших популяций в импактной зоне в условиях антропогенного давления

в зависимости от времени

Заключение. В разработанной модели нестабильность среды обитания популяций вызвана антропогенным давлением. Кризисная ситуация моделируется снижением количества доступного ресурса, уменьшением рождаемости и повышением смертности. Межвидовые взаимодействия, такие как конкуренция, хищничество, протокооперация, не учитываются. Тем не менее, из этой модели следует, что нестабильность биоразнообразия при внешнем пуляцию может быть вызвана как изменением внутреннего метаболизма организма, так и перестройкой структуры популяций в целом. Разработанная модель позволяет объяснить и возможный вариант распре- деления различных видов по численности на территории, подверженной антропогенному воздействию, оценить потери биоразнообразия в зависимости от степени загрязнения территории, и временной интервал, на котором биоразнообразие со- и внутреннем стрессовом давлении на по- храняется.