Математическая модель асинхронного двигателя с эксцентриситетом ротора

Определение связей между диагностируемым дефектом и диагностическим признаком может быть осуществлено экспериментально или на основе математической модели, которая позволит определить эту связь теоретически. Следует учитывать, что математическая модель не может отражать все факторы, характеризующие реальный объект, и поэтому полного соответствия с экспериментом получить не представляется возможным. К достоинству математической модели относится то, что у объекта можно создавать дефекты и изменять степень их проявления. При этом продолжительность расчетов модели занимает значительно меньше времени, чем проведение эксперимента.

Простейшая модель асинхронного двигателя имеет вид двухфазного электромеханического преобразователя с двумя обмотками на статоре и роторе, сдвинутыми относительно друг друга по фазе на 90° (рис. 1) [2, 3].

Рис. 1. Модель обобщенной электрической машины

Здесь ω rα , ω rβ , ω sα , ω sβ – число витков обмоток ротора и статора по осям α и β соответственно; u rα , u rβ , u sα , u sβ , – напряжения в обмотках ротора и статора по осям α и β соответственно; ω r – угловая скорость ротора.

Для описания модели обобщенной электрической машины справедливы уравнения [2]:

– напряжения r^Sα

Щ- α ^ur β ⁼ ps β

d rsα+dt ^sα

d

— M dt

d

— M dt d rsα+dt ^r α

- Mat

- Lr α^ш 0

^rβ 0)r d r’β+dtLrβ

Мы

d

— M dt

d

— M dt

d

×

Flsα

⎢ ir α _⎥ ⎢ ir β ⎥ ⎣ β ⎦

;

^r'β+ dt ^^sβ

– электромагнитного момента

– движения

M э =Μ( is β ir α

-

is α ir β );

d(0r

_± M_c = э ,

где i rα , i rβ , i sα , i sβ – токи в обмотках ротора и статора по осям α и β соответственно; r rα , r rβ , r sα , r sβ – активные сопротивления обмоток ротора и статора; М – взаимная индуктивность; L rα , L rβ , L sα , L sβ – полные индуктивности обмоток ротора и статора по осям α и β; ω r – угловая скорость ротора; M э – электромагнитный момент; M с – момент сопротивления на валу машины.

Взаимная индуктивность между обмотками ротора и статора описывается выражением

M =           ^(0),

где ω s , ω r – число витков обмоток статора и ротора соответственно; k s , k r – обмоточный коэффициент статора и ротора соответственно; т – полюсное деление; ia – длина пакета активной части ста-

тора; А(в) - удельная магнитная проводимость воздушного зазора, зависящая от угла поворота ротора 0 .

Для моделирования удобно уравнение (1) преобразовать и записать относительно потокос-цеплений и токов:

1 г а

MVra

(LSL

—

dV_s а

dV_r а

1 s а

dt

М² )

—

dt

= U s а

= Ы_г Ча_га

^г ‘га

(LSL

—

—

—

Rs ls а;

^R riГР ;

М² ) ^{; lsP}

М 4_{S а} (L _SL

—

d4 se_

= ^-s p

dt

—

rs l s в;

dV_r в

dt

= ^г ^ г в

Lr^sp

(LSL

—

М² )

—

—

М² ); i r e =

MVrp

(LSL

—

Мэ = (тр/2)(M/L _r)( i S р Ча_га

da>-

—

lrаЧгв); dt

Rriга ^;

М 4_{S а} (L _SL

—

М² );

М² )

—

М'Р р (LSL

—

М ² );

Р

J (Мэ

—

Мс )

где ^га , Ч гр , Ч sа , 4 sp - потокосцепления обмоток ротора и статора по осям а и в; R s = r sa = r se ; R r = r rα = r rβ ; p – число пар полюсов; L r , L s – индуктивности рассеяния ротора и статора соответственно; m – число фаз.

Для математического моделирования электродвигателя с эксцентриситетом ротора необходимо учесть зависимость воздушного зазора δ от угла поворота ротора при смещении его оси на расстояние d от оси статора, определяемую выражением

800) = R — г + dcos00) = 8m + dcos00),

где R, r – радиусы расточки статора и ротора соответственно; δm – номинальный воздушный зазор между ротором и статором; d – смещение осей ротора и статора вследствие эксцентриситета; 6 - угол текущего положения ротора (рис. 2).

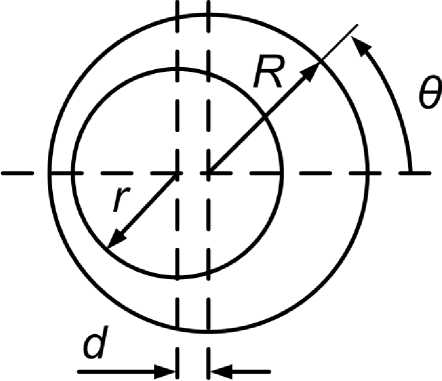
Рис. 2. Эксцентриситет ротора асинхронного двигателя

Цикличное изменение индуктивностей вызывает цикличное изменение сопротивлений обмоток ротора и статора. Вследствие изменения этих сопротивлений появляются пульсации тока статора на частоте fэкс, определяемой выражением экс

= сети (

1±

p

- *,

где f сети – частота напряжения питающей сети; s – скольжение ротора.

При эксцентриситете ротора меняется удельная магнитная проводимость зазора

^З^т(1+£ соѕ(0)), где μ0 – магнитная постоянная; kδ – коэффициент Картера; ɛ = d/δm – относительный эксцентриситет.

С учетом выражения (8) взаимная индуктивность при эксцентриситете ротора определяется выражением

Po

(в)=usksurkrTla ^^(1+£ соѕ(0 )).(9)

С учетом выражения (9) система уравнений (5) примет вид:

^S α       D ; . ^β

α=( ^s^r - Mm (0)); hp =      -    ( ))-Mm (0) ^sa (^s^r - Mm (0));(10)

(     -( ))

Mm ( 9 ) 4^

ir α = ГГ () ( )) ^- M_m ( 0 ) ^sa ⁽ ^s^r ^- Mm ( 0 ));

(     -( ))

Mm (0) ^re lrβ=(LsLr - I'm (9))-Mm (0)^( LsLr - Mm (0 )); э=(   /2)(   ( )/  )(     α- α β);     =․

:           j ( M э-)

Выводы. Полученные математические выражения позволяют смоделировать работу асинхронного двигателя при различных значениях эксцентриситета ротора. В результате расчетов можно получить функциональные зависимости угловой скорости вращения ротора, тока статора и момента на валу в функции времени ω r (t), i(t), M э (t).