Математическая модель асинхронного генератора с автотрансформаторной обмоткой для расчёта несимметричных режимов

Anotation: The article describes the effect of the transformation rate and direction of rotation on the degree demagnetization load current asynchronous generator and the mathematical description of an autotransformer windings connected to star.

Для уменьшения соотношения МДС от токов нагрузки и от возбуждения, следовательно, степени размагничивания тока нагрузки в генераторах известных производителей чаще применяют автотрансформаторный вариант обмотки статора (рисунок 1). Конденсаторы подключаются на более высокое напряжение и при этом возможно использовать меньшую емкость для возбуждения. Существенным недостатком такой обмоткой статора является то, что мощность генератора с автотрансформаторной обмоткой снижается практически пропорционально коэффициенту трансформации [3].

Пользуясь данными математической модели возможно оценить свойства генератора не затрачивая время на выполнение опытов и изменение конструктивных параметров обмотки, т.е. определить конструкцию обмотки генератора с требуемыми параметрами для определенных целей перед выполнением её для исследования, что существенно сокращает сроки разработки обмотки.

В каждой фазе статора АГ имеется две полуобмотки с разными токами. Чтобы преобразовать схему статорной обмотки в автотрансформаторную, представим обмотку одной фазы в виде двух частей, причём одна часть обмотки смещена пространственно относительно другой на угол 9. Емкость возбуждения подключается на напряжение двух полуобмоток, а сопротивление нагрузки к одной из них. Если нагружать только одну часть, то размагничивающее действие от тока активной нагрузки будет меньше, что поясняет рисунок 2 (активные сопротивления частей обмоток не изображены на рисунке). Нагрузив обе части обмотки В1В3 (ток нагрузки в этом случае i В1В3 ), создаем на ней значительное падение напряжения, которое уменьшит напряжение на конденсаторах, что в свою очередь уменьшит возбуждение генератора. Однако, если нагрузить части обмотки В1Н3 и Н3В3 (токи нагрузки в этом случае i В1Н3 и i В3Н3 ), то размагничивающее действие от тока активной нагрузки будет меньше или больше о чём свидетельствует векторная диаграмма рисунок 3 в).

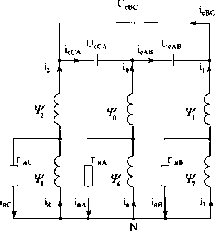
Рисунок 1 – Автотрансформаторная схема статорной обмотки

Учитывая пространственное расположение полуобмоток на статоре АГ может быть два варианта включения нагрузки (рисунок 2 )

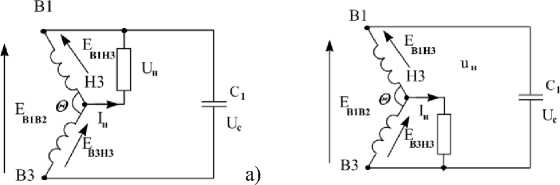
б)

Рисунок 2 – Обмотка одной фазы с подключённой нагрузкой и ёмкостью возбуждения

Токи и напряжения в схеме рисунка 2 можно показать с помощью векторных диаграмм. Вектор тока намагничивания Iµ, создаваемого емкостью С1, опережает эдс ЕВ1В2. Ток нагрузки Iн векторно совпадает с напряжением на полуобмотке, к которой она подключена (рисунок 3).

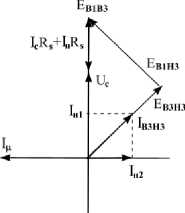
а)

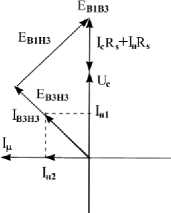
Рисунок 3 – Векторные диаграммы токов и напряжений АГ при автотрансформаторной схеме соединения

Разложение вектора тока I В3Н3 на ортогональные составляющие, одна из которых ( I н2 ) ориентирована по направлению вектора I µ , показывает, что в зависимости от варианта подключения нагрузки I н2 может складываться с I µ (рисунок 3б), то есть создавать эффект дополнительного подмагничивания АГ током нагрузки.

Анализ показывает, что разные варианты подключения (рисунок 3 а,б ) становятся одинаковыми при изменении направления вращения. То есть подключив нагрузку на часть обмотки В3Н3 при правом вращении размагничивающее действие от нагрузки будет больше чем при левом вращении о чем свидетельствуют проекции вектора тока Iн1 и Iн2 векторные диаграммы.

Для подтверждения теоретических предположений был проведено испытание асинхронного генератора с автотрансформаторной обмоткой на базе 4А100S4: D = 0,95 м; l = 0,11 м; I1н = 6,7 А; соsϕн = 0,82; w = 360; kоб = 0,637; Bδ = 0,9 Тл; kµ = 1,65; δ = 0,3 мм; kδ = 1,32; Z/Z2 = 36/28, соотношение ЭДС 266/230 В, емкость возбуждение 18 мкФ по схеме рисунок 1 а). Фаза асинхронного генератора нагружалась до 1,1 кВт, при этом проводились измерения при правом и левом вращении ротора.

Наблюдалось при левом вращении большее значение тока в обмотке и более низкое напряжение на выводах генератора. Если нагрузить другую часть обмотки с потокосцеплением Ψ1, то при правом вращении - большее значение тока в обмотке.

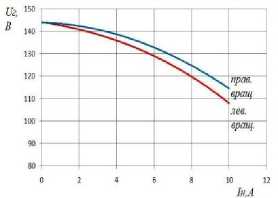
Рисунок 4 – Зависимость напряжения на выводах генератора а) и тока в обмотке б) от тока нагрузки при разном направлении

а)

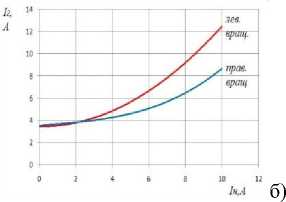
вращения

Авторами было проведено математическое моделирование АГ с автотрансформаторной обмоткой по методике [2]. Система дифференциальных уравнений для схемы статора по рисунку 1 а) следующая id+(1 - к) dr6 - к dr -(1 - к) dr4 = - кл -(1 - к) Ri+к^ +(1 - i) Ri s  dt          s'  dt     s  dt          s'  dt        s  33   '     s’  66    s       4     s’

Ld— + (1 - к ) dV4_ - к d^2. -(1 - к ) dV5_ = - к Ri - (I- к ) r^ + к Ri +(1 - к ) R i s  dt    4      s'  dt      ‘  dt     4      s’  dt         s  114      s’  44     s  2 2   4      s’ к,Г + (1 - к,) Г - к,Г -(1 - к,) Г = -кМ -(1 - к,) Ri + Щ +(1 - к,) Ri s  dt     4      s'  dt      s  dt     4      s'  dt         s  2 2   4      s’  55     s  3 3   4

(1 - ks ) "Г6 = -(1 - ks ) R i6 + r"Ai"A ’ "itT = R icAB ’ dt                             dt

• dr» = _(1-Ил         J-1/ .

• ^{( 1 ks} ) dt      ^{( 1 ks} ) R ⁴ i ^{4 +} r -B i -в ; dt G_B i^cB C ;

• ^{( 1 - k} s ) d d t" = ^{- ( 1 - k} s ) ^R 5 i 5 ⁺ r -C i -C ; d^ thA" = R" ^i=CA .

Чтобы не загромождать рисунок 1 с автотрансформаторной обмоткой, в её частях не изображены их активные сопротивления, но при моделировании они учтены с теми же индексами.

Выразив токи нагрузки i , i и i через токи обмоток и емкостей возбуждения iнВ

i -A

r-Ai-C (i3 + i1 + i2 ) - rHC^cAB + rHA^cBC r-Ar-B + r-Ar-C + r-B r-C ruBiuC (i3 + i1 + i2 )  r-B^cCA + r-C^cAB

;

r -A r -B ⁺ r -A r -C ⁺ r -B r -C

• ■   _ r -A i -B ⁽ i 3 ⁺ i 1 ⁺ i 2 )   r -A ^ cBC ⁺ r -B^UcCA

i-C = rz„ + rz. + rz. нA нB    нA нC    нB нC возможно   решить    систему   уравнений    относительно потокосцеплений фазных обмоток статора и получить потокосцепления обмоток и напряжения на выводах генератора.

Результаты математического моделирования асинхронного генератора с автотрансформаторной звездой представлены на рисунке 5. В модели показан процесс самовозбуждения при ёмкости возбуждения 18 мкФ с подключённой к фазам АГ нагрузкой одинаковой мощности 0,5 кВт, затем, через 1,3 с после включения, на фазе В увеличивается нагрузка до 1,1 кВт.

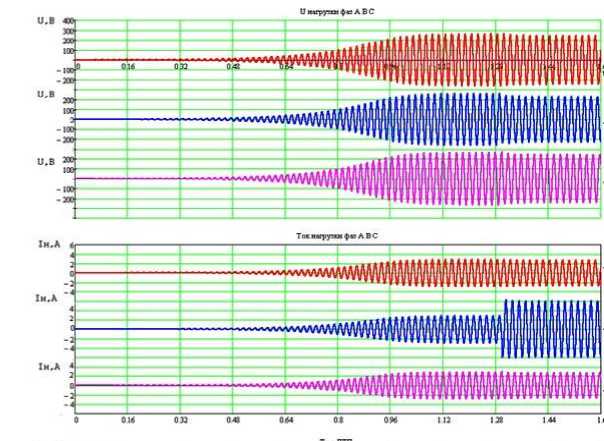
Рисунок – 5 Результаты математического моделирования асинхронного генератора с обмоткой статора соединённой звездой при трёхфазной нагрузке

Математическая модель была проверена на адекватность сравнением расчетных данных по токам и напряжениям обмоток и опытных данных на экспериментальной модели АГ с различным пространственным расположением частей автотрансформаторной обмотки в фазе АГ.

Пользуясь данными математической модели оказалось возможно оценить свойства генератора не затрачивая время на выполнение опытов и получить информацию по таким вопросам, как определение рабочих характеристик генератора в широком диапазоне изменения нагрузки при симметричном и несимметричном подключении однофазной нагрузки, выбор оптимального способа стабилизации напряжения при заданном коэффициенте мощности нагрузки, определение параметров генератора при переходных процессах, значения критических параметров емкости возбуждения и частоты вращения, при которых возможно самовозбуждение.

Результаты математического моделирования подтвердили, что изменение пространственного расположения полуобмоток автотрансформаторной схемы АГ позволяет часть активного тока нагрузки использовать для увеличения или уменьшения магнитного потока машины в зависимости от направления вращения ротора.