Математическая модель асинхронного генератора с обмоткой соединенной звездой для расчёта несимметричных режимов

Введение. Известно, что при несимметрии напряжений приводить трехфазную машину к двухфазной в осях α и β , как сделано в [1] неправомерно, так как в машине появляется эллиптическое магнитное поле. Поэтому расчет несимметричных режимов асинхронных генераторов имеет определенные сложности.

Основная часть. Известна математическая модель идеализированной трехфазной обобщенной машины в осях α, βи γ (рисунок 1 а)) [2]. Нами преобразована данная модель, так как она не адаптирована для расчета несиметричных режимов асинхронного генератора. Так как рассматривается АГ с короткозамкнутым ротором, то её обмотка представляется звездой соединенной накоротко, поэтому напряжение обмотки ротора равна нулю. Рассматривается при моделировании статорная обмотка соединенная звездой (при соединении обмотки статора треугольником появляется дополнительная третья гармоническая составляющая тока), нагрузка подключается на фазы генератора и для возбуждения АГ к обмотке статора подключены конденсаторы, напряжение на них равны напряжению на выводах генератора.

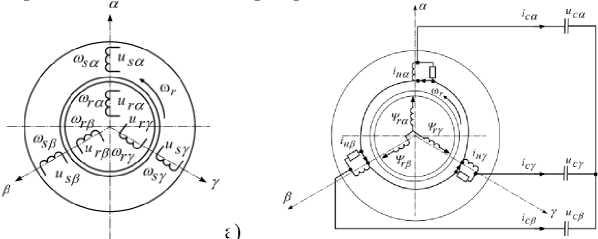
б)

а)

Рисунок 1 - Трехфазная двухполюсная электрическая машина в осях а, р и у, а) и асинхронный генератор в осях а, р и у, б) Преобразованная схема АГ с короткозамкнутым ротором показана на рисунке (1, б) в заторможенной системе 3-фазных координат а, в, у, а система дифференциальных уравнений будет иметь вид:

d V r a dt	— - Rr a	.    Vre — VrT • I--7=----- ra     V-	® r ;	d V „ — dt	- R s a	i a - uca + u c e	d V s a dt	— — R ■ i — r s a s a     H a	i H a .
V	= - R e	;    V r Y — V r a	™ r ;	d V . e	— R . e	i - e - u c e + uc y	d V - e	= — R n i n Y n se se   'ne
dt		ir e      V-		dt			dt		i H e .
d V r , dt dU c a	= - R Y _ ica .	, - Vra "' r Y      -3      r dUc e — i c e . dUc Y		d V s Y — dt — i c Y .	— Rs Y -	i Y - u c Y + u c a .	d V s Y dt	— — R ■ i — r s Y s Y     H Y	iYY ;	(1)
dt	Ca ‘	dt   C e	dt	Cy ’
dtp . "dT	P-^ J Z	- - M ■ f ( B )( i s a	- i Y	+ i s e - i r a	+ i -Y	i r e - i s a - i r e - i	- 1 i “ e r^	M пр I ' I ) +--- s y ra /     r J Z	M c J Z

В описании математической модели для асинхронного генератора при несимметричном режиме приняты следующие допущения. Существует синусоидальное распределение магнитного поля и МДС вдоль воздушного зазора; наличие симметрии магнитопровода относительно осей а, в и у; отсутствие потерь в стали и вытеснения тока в проводниках; независимость сопротивлений рассеяния от пространственного положения ротора; постоянство активных сопротивлений обмоток; токи во всех обмотках переменного тока принимаются синусоидальными и равномерным воздушный зазор генератора.

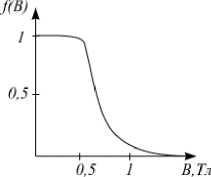
Моделирование различных нагрузочных режимов АГ возможно лишь при учете нелинейности его характеристики намагничивания, что ограничивает возрастание напряжения в математической модели АГ. Поэтому для моделируемой машины был проведен опыт ХХ, результатом которого является определение кривой намагничивания (рисунок 2). При увеличении нагрузки на генераторе происходит уменьшение тока намагничивания, что приводит к изменению взаимоиндуктивности обмоток M о|| . Для того чтобы учесть это изменение с ростом нагрузки определяется функция изменения магнитной связи между обмотками F(В), которая зависит от конструктивных особенностей асинхронного генератора (расположения обмоток в расточке статора, материала сердечника и т.д.), где В – значение индукции в воздушном зазоре. А общий вид этой зависимости, представляемой как M В = M o f ( B ), характеризуется рисунком 3. Возможно определить кривую намагничивания и зависимость F(В) расчетным путем описанным в [4].

При моделировании рассматривается электрическая машина на базе электродвигателя 4А100S4: D = 0,95 м; l = 0,11 м; I_1н = 6,7 А; соs ϕ н = 0,82; w = 360; B δ = 0,9 Тл; k µ = 1,65; δ = 0,3 мм; k δ = 1,32; Z 1 /Z 2 = 36/28 описанный в [3].

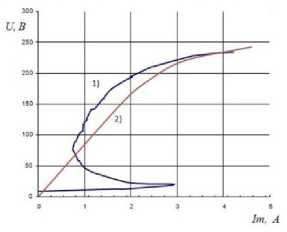
Рисунок 2 – Зависимость тока намагничивания АГ от напряжения на выводах генератора (1 – измеренная, 2 – расчетная).

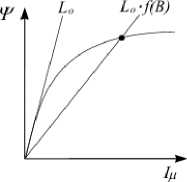
Рисунок 3 - Характеристика намагничивания асинхронного генератора и изменение магнитной связи между обмотками

На основе преобразованной схемы АГ (рисунок 1) составлена схема замещения статорной обмотки, нагрузки и емкости (рисунок 4), система контурных дифференциальных уравнений для которой будет иметь следующий вид:

<

d ^ ₃

dt

—

Ni _

dt

— R 3 i 3 + R 1 i i

d ^   d ^ ₂ _

— — —

dt

d ^ 2

dt

—

u

- cab ;

M _

dt

—

" R 3 i 3

—

нА нА ;

—

—

dt

N з

dt

^du cAB _ X/ i

dt

С

— R i i i + R 2 i 2

—

—

u cBC ;

d^ _

dt

^{— R} 1 i i

—

нВ нВ ;

- R 2 i 2 + R 3 i 3

¹ cab ;

—

u cCA ;

d ^ ₂ _

dt

^{— R} 2 i 2

—

нС нС ’

du cBC _ ¹ ■

.   ^_ _ i

dt

С В

• ■    свс ;

^du cCA _

dt

С С

• ■    сСА *

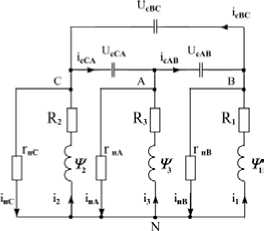
Рисунок 4 - Схема соединения звездой серийной обмотки асинхронного генератора с трехфазной нагрузкой и включением емкостей треугольником

Результатом расчета схемы будут токи i1, i2, i3,, поэтому

необходимо остальные токи выразить через них. При допущении icBA + icCA + icAB = 0, токи i-A, Чв , i-c после преобразования будут равны iнА

r-BZ-C (i3 + z1 + i2 ) - r^BucCA + r-CucAB ; z = r-Ai-C (i3 + Z + i2 ) - r-CucAB + r-AucBC r-Ar-B + r-Ar-C + r-B r-C         ’              r-Ar-B + r-Ar-C + r-Br-C v _ r-Ai-B (i3 + z1 + i2 ) - r-AucBC + r-BucCA i-C =                                                  .

r -A r -B ⁺ r -A r -C ⁺ r -B r -C

Матрица M _В учитывает взаимное расположение обмоток в расточке статора АГ. В результате решения системы (2) определяются значения потокосцеплениий всех обмоток АГ. Их величины можно представить вектором ||ф||, размер которого зависит от числа обмоток АГ. Составление матрицы индуктивностей и взаимных индуктивностей электрической машины описано в [2] и запишется в виде

' Ls   - 0.5 M - 0.5 M M   - 0.5 M - 0.5 M ^

• - 0.5 M   Ls   - 0.5 M - 0.5 M M   - 0.5 M

• - 0.5 M - 0.5 M Ls   - 0.5 M - 0.5 M   M

М_в =                                                  .

В M   - 0.5 M - 0.5 M   Lr   - 0.5 M - 0.5 M

• - 0.5 M   M   - 0.5 M - 0.5 M Lr   - 0.5 M

• ( - 0.5 M - 0.5 M M   - 0.5 M - 0.5 M Lr J

Токи обмоток АГ находятся в результате решения системы алгебраических уравнений методом обратной матрицы

ill = 1 M»l Г*-Mk

где MBB\ Г  " обратная матрица взаимоиндукции между обмотками АГ.

Для уменьшения времени расчета перерасчет взаимоиндуктивности происходит каждый полупериод и используется действительное значение. Это позволяет существенно сократить время расчета точек осциллограммы.

Таким образом с учетом насыщения, определяются токи всех обмоток АГ при нессиметричных подключениях нагрузки, после этого возможно определить напряжения при решении системы дифференциальных уравнений.

Таблица 1 – Результаты расчета обмотки соединенной звездой с включением нагрузки на одну фазу

f , Гц	RВ , Ом	IА , А	IВ , А	IС , А	U a , В	U b , В	U c , В
50	30	2,42	6,41	2,6	218,3	192,3	207,0

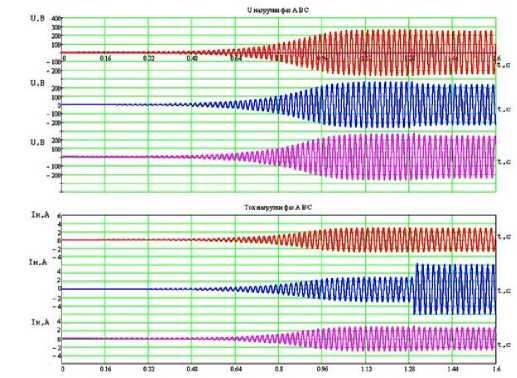
Рисунок 5 - Результаты математического моделирования асинхронного генератора с серийной обмоткой статора соединенной «звездой» при трехфазной нагрузке

Результатом математического моделирования асинхронного генератора с серийной схемой обмотки соединенной «звездой» представлены на рисунке 5 и в таблице 1. Для удобства оценки адекватности модели амплитудные значения приведены к действующим значениям. В модели показан процесс самовозбуждения при емкости возбуждения 60 мкФ с подключенной однофазной нагрузкой одинаковой мощностью 0,5 кВт, затем на фазе В увеличивается нагрузка до 1,1 кВт. При этом напряжение по фазам уменьшается, в связи с этим токи фазах А и С немного уменьшаются, а ток в фазе В увеличивается. Магнитное поле машины искажается подобно эллипсу, так как появился несимметричный режим, поэтому напряжения фазные имеют разные значения, причем меньшее из них принадлежит более нагруженной фазе В.

Заключение. Таким образом математическая модель отражает реальное изменение электрических параметров асинхронного генератора при несимметричном подключении нагрузки. Перерасчет взаимоиндуктивности происходит каждый полупериод и используется действительное значение, поэтому существенно сокращается время расчета математической модели асинхронного генератора и появляется возможность рассматривать значительный расчетный период с построением осциллограмм токов или напряжений, а также построения характеристик электрической машины.

MATHEMATICAL MODEL OF ASYNCHRONOUS GENERATOR WITH STAR CONNECTED WINDING FOR CALCULATION OF ASYMMETRICAL MODES

Annotation: The article presents the mathematical model of the induction generator under unbalanced load with the non-linear characteristics of magnetization. The system of the differential equations under certain assumptions made by basis of the transformation scheme of the axes α , β and γ , describes the method of calculating the iduction generator based on squirrel-cage motor series 4А100S4 with the connection stator winding to star and the inclusion with the triangle. The matrix of inductances and mutual inductances of the electric machine is composed. The results of calculation in the form of oscillograms of currents and voltages are presented.