Математическая модель автоматической системы обработки багажа аэропорта со значительными трансферными пассажиропотоками

ПОСТАНОВКА ЗАДАЧИ

Решается задача формирования аналитической модели АСОБ узлового аэропорта (хаба), обслуживающего значительные транферные и транзитные пассажиропотоки. Использование высокопроизводительных АСОБ позволяет аэропорту снизить значение такого показателя, как минимальное стыковочное время (МСТ), представляющего собой минимальное время, за которое аэропорт пересадки и авиакомпания-перевозчик гарантируют обслуживание трансферного пассажира и обработку его багажа. Наиболее бурно развивающиеся европейские хабы способны обеспечить значения МСТ, составляющие 20-30 мин, что является их важным конкурентным преимуществом.

Требуется сформировать математическую модель АСОБ, не предполагающую необходимости выполнения процедуры имитационного моделирования, которая позволяет получать оценки важнейших характеристик процесса обработки багажа различных категорий, таких как длительность пребывания багажа в системе, величины очередей, степень загрузки элементов системы и др. Модель должна учитывать специфику функционирования АСОБ в аэропорту со значительной долей трансферных пассажиров и багажа.

КОНСТРУКЦИЯ И ФУНКЦИИ АСОБ

Современные АСОБ поддерживают весь цикл терминальных процедур обработки багажа: прием, маркировку и взвешивание на этапе регистрации; хранение заранее сданного багажа; доставку в помещения досмотра и сортировки;

многоступенчатый полный досмотр и изъятие подозрительного багажа; сортировку по рейсам; срочное перемещение первоочередного багажа; выдачу; обработку багажа отложенного или отмененного рейса и др.

При всем разнообразии индивидуальных технических решений АСОБ общие принципы их конструкции сходны – места багажа (МБ) перемещаются с помощью ленточных конвейеров или тележек, управление осуществляется с использованием компьютерных информационных систем. В высокопроизводительных дорогостоящих АСОБ носителями МБ на всех этапах его обработки служат тележки, оснащенные опрокидывающейся платформой либо фрагментом ленточного конвейера. Скорость движения тележек с МБ составляет 1.5-7.0 м/с и более. Конвейеры применяются в менее сложных системах. Скорость движения лент конвейеров 0.5-2.0 м/с [1]. Для повышения производительности АСОБ при сохранении ее приемлемой стоимости эти два типа носителей могут использоваться совместно: система тележек применяется только для сортировки МБ, при выполнении всех остальных операций МБ перемещается конвейерами.

В роли носителя информации о назначении МБ выступает багажная бирка. Используются различные виды кодирования – штриховое, магнитное или радиочастотное. При прохождении мимо декодирующих сортирующих устройств МБ или тележки с МБ автоматически направляются на соответствующие линии.

АСОБ включают в качестве функционального компонента автоматизированную систему контроля багажа, в которой МБ проходит несколько стадий досмотра. “Ручной” досмотр предполагается только на последней стадии и только для МБ, вызвавших “подозрение” на начальных стадиях. Для ускорения процесса проверки внедряются новые типы технических сис- тем, таких как автоматические системы обнаружения взрывчатых веществ (Explosives Detection System, EDS).

Ниже рассмотрена конвейерная АСОБ для аэровокзалов средней пропускной способности с тремя стадиями досмотра МБ с применением типового рентгено-телевизонного досмотрового оборудования (интроскопов). Первая стадия предусматривает применение технологии досмотра МБ “в потоке” (“in-line контроля”). Вызвавшие подозрение МБ направляются на другой интроскоп для прохождения дополнительного сканирования (вторая стадия досмотра). При снятии подозрений эти МБ возвращаются в поток, а при подтверждении подозрений они подвергаются визуальному контролю со вскрытием (третья стадия досмотра).

Продолжительность первой стадии досмотра обусловлена техническими характеристиками интроскопов. Для наиболее распространенных моделей скорость движения ленты конвейера находится в пределах 0.2-0.5 м/с, длина ленты – около 3 м.

Досмотр второй стадии производится не “в потоке” (“off-line”), что предполагает значительное число манипуляций, которые невозможно автоматизировать без использования дорогостоящей технологии EDS, и, соответственно, значительные временные затраты. Средняя продолжительность второй стадии досмотра одного МБ – около 3-4 мин [2].

Третья стадия досмотра практически выполняется вне АСОБ, поэтому ее продолжительность не влияет на временные характеристики обработки багажа в АСОБ.

Помимо интроскопов рассматриваемая конвейерная АСОБ включает следующие основные компоненты:

• -    место регистрации, состоящее из стойки регистрации, взвешивающего и маркировочного конвейеров;

• -    коллекторные конвейеры, предназначенные для сбора МБ, поступающих от различных стоек регистрации, в общий поток;

• -    транспортировочные конвейеры, доставляющие поток МБ к местам обработки;

• -    конвейеры очереди, предназначенные для обеспечения ритмичного и равномерного поступления потока МБ к местам обработки без необоснованной остановки системы;

• -    сортировочные конвейеры, предназначенные для распределения потока МБ, прошедших досмотр, по направлениям вылета;

• -    реверсивные конвейеры, предназначенные для поворота направления потока МБ;

• -    гравитационные рольганги, рассчитанные на накопление МБ, имеющих общие признаки -

• забракованные или по месту назначения;

• -    вертикальные отводящие конвейеры (сбрасыватели), предназначенные для перемещения отдельных МБ с транспортировочного конвейера на гравитационные рольганги. Представляют собой вертикально расположенные ленточные конвейеры, способные с помощью электродвигателя поворачиваться относительно одного из своих концов. При получении команды на извлечение определенного МБ из общего потока сбрасыватель, исходно расположенный параллельно потоку МБ транспортировочного конвейера, разворачивается и, перегораживая ленту транспортировочного конвейера, смещает МБ на рольганг после чего возвращается в первоначальное положение. Время срабатывания сбрасывателя – около 3-4 с;

• -    система управления, предназначенная для автоматической реализации алгоритмов управления потоками МБ с использованием “виртуальных ячеек”. При поступлении каждого МБ в АСОБ программно создается “виртуальная ячейка”, в пределах которой на ленте конвейера находится МБ. Система управления “создает” “виртуальную ячейку” и следит за движением ее по конвейерам, исключая опасность столкновения МБ при перемещении с конвейера на конвейер. Длина “виртуальной ячейки” - около 1-1.5 м.

СОБ КАК СЕТЬ

МАССОВОГО ОБСЛУЖИВАНИЯ

Аэропортовая АСОБ рассматривается как разомкнутая СеМО, в которой МБ выступают в роли заявок, а блоки системы (конвейеры различных типов, интроскопы и т.п.) – в роли одноканальных систем массового обслуживания (СМО). Поскольку временные характеристики процесса обработки багажа трансферных пассажиров представляют особый интерес, то багаж этой категории отнесен к отдельному классу заявок. Исследуется функционирование АСОБ в течение периода пиковой нагрузки, когда интенсивность поступающего потока багажа может считаться постоянной.

Среднее время пребывания заявки в СеМО, включающей N СМО, определяется по известной формуле [3]

N

Т = nt- » T Z Gi^1    , i=1

где G i – интенсивность входного потока заявок для i -й СМО. Под входным понимается поток заявок, поступающих на вход отдельной СМО из внешней среды СеМО, а не с выхода какой-либо

СМО; X i - интенсивность потока заявок в i -й СМО; T i - среднее время пребывания заявки в i -й СМО.

В общем случае среднее время пребывания МБ в i -м блоке АСОБ представляет сумму

T i = T Д j + T Oi + T ni , где Т Дi – время движения МБ в i -м блоке; T Oi – средние затраты времени на различные остановки в i -м блоке, в течение которых МБ не продвигается по конвейеру и не подвергается какому-либо другому обслуживанию, а н е подвижно ожидает дальнейшего перемещения; T П i – средние затраты времени на выполнение различных форм обслуживания МБ, помимо перемещения по конвейеру.

С учетом различия операций по обработке багажа разобьем множество блоков АСОБ B = { 1 , 2 ,...,i,...,N } на непересекающиеся подмножества, такие что

Bi о В 2 о В з = В, где B1 – подмножество блоков, в которых возможно только перемещение заявок с постоянной скоростью в течение времени TД ; B2 – подмножество блоков, в которых перемещение заявок с постоянной скоростью может многократно пре- рываться остановками, имеющими среднюю суммарную длительность TО , и возобновляться; B3 – подмножество блоков, в которых помимо перемещения и ожидания, могут производиться другие процедуры обработки багажа.

В подмножество B ₁ включены коллекторные, транспортировочные, реверсивные, сортировочные конвейеры, а также досмотровые аппараты первой стадии, использующие технологию досмотра багажа “в потоке” (“in-line”). Для этих блоков системы, не обладающих возможностью накоп л ения неподвижных требований, принимается То- = 0 .

Подмножество B ₂ охватывает однотипные блоки – конвейеры очереди, в каждом из которых продолжительности ожидания каждого МБ T О i являются случайными величинами. В отличие от времени ожидания, затраты времени на движение в блоках - элементах подмножеств B ₁ и B ₂ , являются величинами неслучайными и определяются как

Tд-= LiVi, где Li и Vi - длина и скорость движения конвейера, соответствующего i-му блоку (кроме блоков повторного досмотра). Длина конвейеров очереди определяется их вместимостью: max

Li   lячinnOi ’ i е B2’ где lяч i – длина ячейки на ленте i-го конвейера очереди, nОmiax – максимальное число ячеек – вместимость i-го конвейера очереди.

Подмножество B ₃ включает только досмотровые аппараты второй фазы. Длительность повторного досмотра не “в потоке”, представляющая собой случайную величину со значительным разбросом, как правило, значительно отличается от времени простого перемещения МБ по ленте досмотрового аппарата, кроме того в ней затруднительно выделить отдельные составляющие, такие как время движения, время ожидания и пр., поэтому в данном случае целесообразно принять

T i = M [ t docM ] i , где M [ t g_0CM ] i - среднее время пребывания МБ в блоке повторного досмотра, имеющем порядковый номер “ i ” среди всех блоков АСОБ.

Таким образом, время пребывания заявки в i -м блоке определяется одним из трех способов, в зависимости от принадлежности блока к одному из трех подмножеств:

Т Д i , i е B i ,

Т i =\ Т Д i + T Oi , i е B 2 ,

^Тдосм i’     i ^{е B} 3 .

Интенсивности потоков заявок в СМО СеМО определяются в результате решения матричного уравнения баланса сети

A • Л = G , (1) где Л = ( X 1 X 2 ... X n ) T — матрица-столбец искомых интенсивностей потоков в блоках, G = ( ^G 1 G 2 ... G n ) T - матрица-столбец входовых интенсивностей.

Решение уравнения (1) в матричном записывается как

Л = A ^{- 1} • G .

Элементы квадратной матрицы А определяются с учетом следующих свойств слияния и разветвления потоков. При слиянии n потоков с интенсивностями X i ,..., X n образуется поток, имеющий интенсивность X = X i + ... + X n . При ветвлении потока l на n направлений, вероятности перехода заявки в которые равны p ₁ ,..., p n , образуется n потоков с интенсивностями X p i ,..., X p _n , соответственно.

Среднее время обработки трансферного МБ, вошедшего в систему в k -м блоке, определяется по известной формуле для входового среднего времени пребывания в сети [3]:

N

Т Т k = X e ki T i,

_                    i=i где ТТ k – входовое среднее время пребывания в сети, т.е. среднее время пребывания в сети заявки, поступившей из k-го входного потока

( k = 1 , 2 ,...,N ) , 6 ki - передаточные коэффициенты. Значения 6 ki , равные среднему числу приходов в i -ю СМО заявок из k -го входного потока, определяются из матричного уравнения, по структуре аналогичного (1):

е t = a-1 • g v где 0 к =(6 k 1 6 к 2 ... 6 ki ... 6 kN )T -матрица-столбец передаточных коэффициентов k-го входного потока, Gk =(Gki Gk2 ... Gki ... Gkn)T - матрица-столбец, элементы которой определяются в соответствии со следующим правилом

G ki = *

1 ,

0 ,

k = i, k * i.

i = 1 , 2 ,...,N .

Область применимости описываемой модели ограничена стационарным состоянием СеМО, которое, при постоянстве интенсивностей входящих потоков, может быть нарушено только в случае использования в СеМО блоков, обладающих недостаточной пропускной способностью. Условие стационарности СеМО записывается как к - Х i k з i =     ^ 1, i = 1, 2 ,...,N,

Ф i где kзi – коэффициент загрузки i-й СМО, фi = Vi[lяЧi - пропускная способность i-й СМО.

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ОЧЕРЕДЕЙ

В рассматриваемой СеМО образование очереди возможно в местах:

• -    входа простейшего потока заявок в СеМО;

• -    слияния нескольких потоков;

• -    перехода заявки из СМО, обладающей большей пропускной способностью, в СМО с меньшей пропускной способностью;

Под местами входа потоков багажа в АСОБ понимаются начальные секции транспортеров очереди, расположенных за стойками регистрации пассажиров, которые накапливают багаж и направляют его далее к коллекторным и транспортировочным конвейерам. Манипуляции по оформлению МБ, выполняемые на местах регистрации, относятся к процессам обслуживания пассажиров, поэтому затраты времени на их выполнение не включаются в общую длительность пребывания МБ в АСОБ.

Места второго типа представляют собой участки входа на конвейер, по которому движется поток 1 интенсивностью Х^, потока 2, имеющего интенсивность Х2 (рис. 1). Поток 2 может яв- ляться входовым, поступающем извне рассматриваемой СеМО, например, со стоек регистрации. В этом случае он сохраняет все свойства простейшего потока. Также поток 2 может поступать на главный конвейер с другого (второстепенного) конвейера, перемещающего с постоянной скоростью V2 ячейки длиной lяч2 . Ячейки второстепенного конвейера поступают к главному через фиксированные интервалы времени длительностью lяч2 V2 . Поскольку каждая ячейка может как содержать, так и не содержать заявки, то интервалы времени между прибытиями заявок потока 2, к месту перехода на главный конвейер представляют собой случайные величины, кратные lяч2 V2 . Подобная “регуляризация” потока приводит к нарушению требования отсутствия последействия, предъявляемого к простейшим потокам, что не позволяет считать поток 2 простейшим и не дает возможности использовать в расчетах известные аналитические модели теории массового обслуживания.

Вероятность образования очереди приводит к необходимости размещения в месте слияния потоков конвейера очереди, состоящего из набора отдельных конвейерных секций длиной по l яч О , способных работать и отключаться раздельно. Такая конструкция позволяет немедленно перемещать багаж далее в случае наличия свободных ячеек на главном конвейере, либо накапливать очередь в виде цепочки МБ без разрывов между ними. Описанное устройство не искажает свойств потока 2.

Для оценки средней длительности задержки заявки, поступающей из потока 2, предлагается следующая формула, полученная эмпирическим путем на основе известной формулы для времени задержки заявки в одноканальной СМО:

Ф 1

T O

2(Х1 -ф1 )(Х1 +Х2 -ф1) ,     (2)

где V ₁ и l яч ₁ – соответственно, скорость движения и размер ячейки главного конвейера, Ф 1 = V 1 /I_яч 1 – пропускная способность главного конвейера.

Рассматриваемая СеМО стационарна, если

Х ₁ + Х ₂ выполняется условие k _з =-------< 1 .

1        _{ф 1}

Количество секций конвейера очереди n Omax должно с заданной надежностью обеспечивать

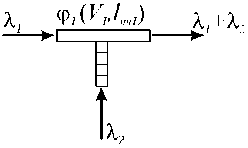
Рис. 1. Место слияния двух потоков заявок бесперебойное продвижение багажа к главному конвейеру. Расчетная вероятность отказа в обслуживании МБ, вызванная отсутствием места на транспортере очереди, PР должна быть достаточно малой. Потребная вместимость nOmax находится из условия

( П о <  24 ) для оценки параметра р используется приближенная формула [4]

* p

» 1 -

1 +

3 V

-

*

1п\ПО + 1 _* _

—^--¹ п_о + 2

16 ^О

У

*

^по + 1 ) ,(5)

P ( n § >  n Oax ) < P p ,         (3)

г д е n _О

р

*

– выборочное значение параметра р ,

X 2 T o — выборочное среднеечисло заявок

где n OФ – фактическое число МБ в очереди,

Ф max

P (nO > nO )

– вероятность того, что фактичес-

кое число МБ в очереди превысит вместимость конвейера очереди, P Р – заданная расчетная вероятность сбоя в работе конвейера очереди.

max

Для определения n O предлагается апп-

роксимировать число мест в очереди перед слиянием двух потоков багажа целочисленным логарифмическим распределением.

Функция логарифмического распределения для случайной величины n O , область возможных значений которой определяется как n o = 0 , 1 , 2 ,... , задается выражением

в очереди.

Итак, потребное число n Omax подбирается с использованием (4), (5) как минимальное, удов-летворяющееусловию 1 - F ( n o ) < P p .

Представленное в табл. 1 сравнение результатов формул (2), (4), (5) и материалов имитационного моделирования функционирования АСОБ свидетельствует о высокой точности предложенного алгоритма в случае простейшего потока 2. В случае, когда поток 2 поступает с транспортера и не может считаться простейшим, относительная ошибка 5 т формулы (2) достигает существенных значений, однако абсолютные отличия расчетных значений от модельных

0 ,

F(nO ) =

довольно малы, так, по времени ожидания разница не превышает 1 с.

Примером мест третьего типа служат места сочленения транспортировочных конвейеров и досмотровых аппаратов второй стадии, которые в некотором приближении могут рассматриваться как одноканальные экспоненциальные СМО с очередью, число мест в которой ограничено величиной n Omax . Среднее время ожидания обслуживания в таких СМО определяется как [3]

nO < 0, k < nO < k+1, k = 0,1,2(4)

k i + ^{+ 1}

У.p— in1p) i=o i+1

^ i

где р - параметр распределения, 0 <  p <  1 .

При относительно малых выборочных средних значениях числа заявок в очереди

Таблица 1. Результаты аналитической и имитационной моделей

Параметры	Варианты
	1 2 3 45678								9	10	11	12
Поток	простейший								«регулярный»
V 1 , м/с	1						0.5			1
l яч 1 , м	2						2			2
Ф 1 ,    1/с	0.5						0.25			0.5
V 2 , м/с	-								1
l яч 2 , м	-								2
Х 15    1/с	0	0.08	0.16	0.24	0.32	0.40	0.07	0.14	0.17	0.08	0.25	0.4
X 2,   1/с	0.08						0.03			0.02	0.05	0.08
kз 1	0.16	0.32	0.48	0.64	0.80	0.96	0.40	0.67	0.80	0.20	0.60	0.96
расч T О    , с	1.19	1.74	2.79	5.19	13.09	96.00	4.55	12.86	30.00	1.50	5.00	96.00
мод T О   , с	1.19	1.74	2.81	5.17	13.12	96.02	4.56	12.77	31.45	2.47	5.88	99.20
5 Т , %	0.0	0.1	0.6	0.4	0.2	0.0	0.4	0.7	4.6	39.2	15.0	3.2
расч nО	4	4	6	9	17	179	5	9	20	2	6	179
nО мод	3	3	5	7	15	189	4	9	17	2	5	175

Т О =x r ² 1 — ( x r )'

max

) n o + n m

-if г {       \ И) —1

_ v _х_и max L , -xL max j I

;“ ( x r — 1\ л т ) n O . ' л. /' - 1 ( x r : n O ) - 1 / ,

где l – интенсивность потока требований, Т – среднее время обслуживания;

Вероятность того, что фактическое число МБ в очереди n OФ может превысить максимально допустимое число n Omax , определяется по известной формуле [3]

Ф max

Pno > no )=(XT

^^^^^^^^

max m

1\xr)nO .(xr)(nO

- 1

^^^^^^^B

Откуда, учитывая (3), рассчитывается потребное число секций конвейера очереди

max n _O

^^^^^^^B

log x T ) ( P P ( ^{x т} ) 2 —^{( x T ) 2} +^{x T} P - ¹ ! ,

где p" - оператор округления до ближайшего большего целого.

МОДЕЛЬНЫЙ ПРИМЕР

Рассматривается АСОБ с тремя стадиями досмотра и сортировкой багажа на замкнутом сортировочном конвейере с применением сбрасывателей, блок-схема которой приведена на рис. 2. МБ на коллекторный конвейер поступают с шести конвейеров очереди, пять из которых отводят потоки багажа первоначальных пассажиров интенсивностью G П от десяти стоек регистрации (по две стойки на один конвейер). По шестому конвейеру поступает поток трансферного багажа интенсивностью G Т . Потоки багажа стационарны. Одновременно производится сортировка багажа на 5 рейсов однотипных ВС на 5 рольгангах-накопителях.

Ниже приводятся принятые значения характеристик модельной СОБ. Использованная в обозначениях элементов АСОБ индексация имеет следующую расшифровку: “ О ” - конвейер очереди, “ Т ” – транспортировочный конвейер, “ К ” -коллекторный конвейер, “ С ” – сортировочный конвейер. Если индекс не сопровождается номером блока, то указанная величина имеет отноше-

ние ко всем блокам данного типа.

Длины ячеек конвейеров: l ячо = 1 м , ¹яч р = ¹ м , ¹ ячС = ⁴ м .

Длины конвейеров (их участков): L / 7 = 2 м, L / 14 = L / 18 = 4 м L k = 2 м, L Д = 3 м •

Скорости лент конвейеров: V_o = Vk = 0.5 мс , V / = V c = 1 мс , VД = 0 . 25 м/с .

Среднее время второй фазы досмотра M [ г доем ] = 180 с .

Доля МБ, направленных на вторую фазу досмотра Р 1 = 0 . 03 . Предполагается, что МБ, забракованных на второй фазе досмотра и не прошедших по этой причине сортировки, нет.

Регистрация выполняется по свободной схеме, поэтому МБ, принятые на любом месте регистрации, а также трансферные МБ могут с равной вероятностью поступить на любой рольганг. Таким образом, вероятность перехода МБ на один из пяти рольгангов Р 2 = 1/5 .

Значения входных интенсивностей и средних затрат времени на пребывание МБ в блоках модельной АСОБ определяются по следующим формулам (см. стр. 132, выражения над матрицей А ).

Уравнения баланса интенсивностей потоков для нескольких выбранных блоков приводятся ниже:

Блок 1:      2 G 1 = Л 1.

Блок 18:    0 = - ( 1 - Р 1 ) Л 17 +Л 18.

Блок 10:    0 = —X 2 — X 9 +Лю .

Блок 28:    0 = ^р 2 ^x 26 ^{— x} 27 ^{+ x} 28.

Полученная на основании полной системы уравнений баланса интенсивностей квадратная матрица А для рассматриваемой АСОБ имеет следующий вид (см. ниже, стр. 132).

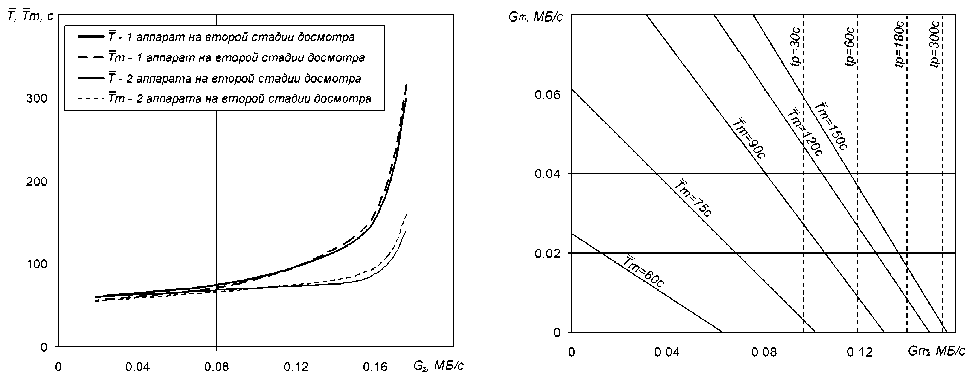
Результаты расчетов временных характеристик модельной АСОБ для различных уровней интенсивностей багажных потоков представлены на рис. 3. Проведенное для описанного набора исходных данных имитационное моделирование в среде GPSS World на длительном интервале модельного времени позволило выявить достаточно высокую точность аналитических расчетов – во всем диапазоне интенсивностей потоков ошибка не превысила 1.2%.

Рис. 3а ото б ражает зависимости общей Т и трансферной Т Т средних продолжительностей

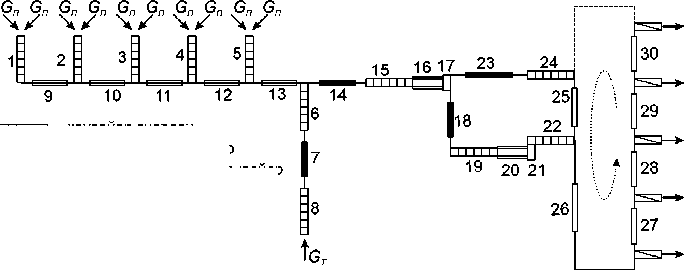
Рис. 2. Блок-схема модельной АСОБ

rm~m - конвейер очереди ।    ।— коллекторный конвейер

^— транспортировочный конвейер

-и ।— сортировочный конвейер r---..j - рольганг

[=| - интроскоп

J - реверсивный конвейер

пребывания МБ в АСОБ от суммарной интенсивности G ^ поступающих потоков багажа ( G ₂ = 10 • G n + Gt ). Резкий рост кривых в правой части графика соответствует выходу на ограничение по пропускной способности АСОБ. При загрузке АСОБ выше 80%, длины очередей и временные характеристики процесса обработки багажа становятся неудовлетворительными. Как показали расчеты, роль “бутылочного горлышка” модельной системы играет интроскоп второй стадии досмотра. Использование двух интроскопов на этой стадии позволяет значительно улучшить показатели системы (см.рис. 3а). Другим направлением снижения затрат времени на обработку багажа является использование багажных тележек на этапе сортировки (по результатам расчетов снижение составит до 25%).

Длительности обработки как трансферного, так и начального багажа в АСОБ зависят от соот- ношения интенсивностей потоков этих категорий багажа. Для модельной АСОБ характер влияния на ТТ интенсивности трансферных МБ GT и суммарной интенсивности начальных МБ Gn£ = 10 • Gn проиллюстрирован рисунком 3б. Как показало имитационное моделирование рассматриваемой АСОБ, средняя задержка трансферных МБ на 2 мин приводит к тому, что приблизительно 2.5-3% этих МБ находится в системе не менее 5 мин, а около 1.5-2% - не менее 10 мин, что составляет внушительную и не всегда удовлетворительную величину для хаба, декларирующего МСТ в пределах 20-30 мин. Это означает, что пропускная способность АСОБ, предназначенной для функционирования в аэропорту со значительной долей трансферных пассажиров, должна превышать пропускную способность багажной системы “обычного” аэропорта с аналогичным суммарным уровнем пассажиропотока.

0 ,

	l ЯЧО n Oma V O + TOi >	i = 16 > 8 > 15 > 19 >  22 >  24 >	( конвейеры очереди )
	L Ti VT >	i = 7 > 14 > 18 >  23 >	( транспортировочные конвейеры)
	L Ki VK >	i = 9 > 13 >	( участки коллекторного конвейера )
T =j	L Д V Д ,	i = 16 >	( интроскоп первой фазы )
	M [ ^ досм ] >	i = 20 >	( интроскоп второй фазы )
	l яч Р V Р ,	i = 17 >  21 >	( реверсивные конвейеры )
	l яч cFc >	i = 25 > 30 .	( участки сортировочного конвейера )

А =

f 1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0 1
0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	1	- 1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	1	- 1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
- 1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	- 1	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	- 1	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	- 1	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	- 1	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	- 1	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- Р 1	1	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	( 1 - P 1 )	0	0	0	0	0	1	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	1	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- 1	0	0	- 1	1	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	- ( 1 - P 2 )	1	0	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	P 2	- 1	1	0	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	P 2	0	- 1	1	0
. 0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	P 2	0	0	- 1	1 ,

2 G П ,

G i = 1 ^G t ,

i = 1 , 5

i = 8, i = 6,7, 9.30,

б)

а)

Рис. 3. Зависимости времени пребывания МБ в модельной АСОБ от:

а – суммарной интенсивности потоков МБ;

б – соотношения интенсивностей потоков МБ трансферных и первоначальных пассажиров

Проектирование АСОБ и системы обслуживания начальных пассажиров должно производиться совместно. Дело в том, что число мест регистрации и, следовательно, число конвейеров очереди является проектной характеристикой АСОБ и влияет на длительность обработки багажа. С другой стороны, оптимальное число мест регистрации рекомендуется определять исходя из заданных требований качества обслуживания пассажиров – предельного времени ожидания в очереди t P и вероятности превышения этого времени P зад . На основе известных методик [5] для модельной АСОБ определены значения G n ^ , соответствующие Р зад = 0 . 01 и различным t p , отображенным на рис.3б. Результаты говорят о недостаточной сбалансированности пропускных способностей АСОБ и системы обслуживания пассажиров. Следует либо сократить чрезмерное число стоек регистрации, не отвечающее общепринятым стандартам качества обслуживания пассажиров, либо увеличить пропускную способность АСОБ, например, путем установки дополнительного интроскопа второй фазы досмотра.

Разработанная аналитическая модель может быть использована для проектирования, анализа и оптимизации параметров систем, реализующих различные технологические схемы обработки багажа в узловых аэропортах.