Математическая модель цифровой релейной электромеханической системы управления вектором тяги жидкостного ракетного двигателя

В системах управления движением пилотируемых космических кораблей особое место занимают специальные подсистемы, отвечающие за управление угловым положением камер сгорания маршевых жидкостных ракетных двигателей (ЖРД) этих изделий в плоскостях стабилизации. Каждая из таких подсистем, получивших название «системы управления вектором тяги» (СУВТ), включает в себя, как правило, два канала управления, или рулевых тракта (РТ).

Очень часто для управления вектором тяги летательных аппаратов различного назначения применяются цифровые релейные электромеханические СУВТ [1], характеризующиеся тем, что напряжение на их рулевые машины (РМ) или электроприводы подаётся только в том случае, когда сигнал рассогласования достигает определённого значения. Поэтому такие СУВТ обладают определённой зоной нечувствительности по отношению к входному сигналу. Достоинствами таких СУВТ являются их простота, надёжность и возможность получения оптимальных траекторий движения исполнительных органов. К недостаткам следует отнести их склонность к колебаниям и наличие определённой нечувствительности (неточности) при слежении.

Рациональный выбор алгоритмов управления такой цифровой релейной электромеханической СУВТ может быть достигнут путём проведения системного анализа и параметрической оптимизации, а составляющими элементами системного анализа являются декомпозиция системы на составляющие элементы и последующее агрегирование математической модели этой системы [2].

В настоящей работе ставятся следующие задачи:

• •    декомпозиция СУВТ на составляющие функциональные элементы;

• •    агрегирование нелинейной математической модели СУВТ, отражающей два динамических режима её работы;

• •    апробация разработанной математической модели динамики СУВТ.

декомпозиция СуВТ на составляющие функциональные элементы

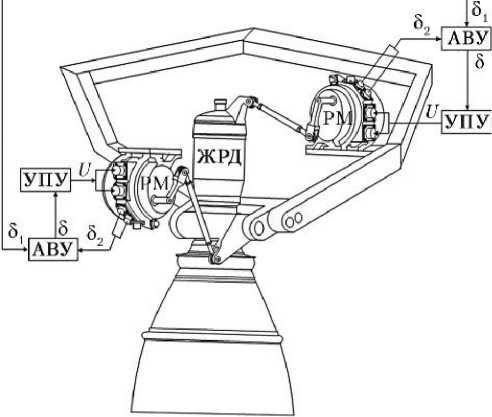
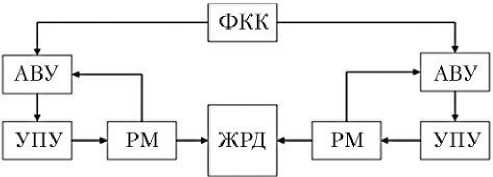
Конструкционно-функциональная схема СУВТ пилотируемого транспортного корабля и декомпозиция СУВТ на функциональные элементы представлена на рис. 1.

СУВТ имеет два РТ, один из которых управляет углом поворота камеры ЖРД в плоскости тангажа, а второй — в плоскости рысканья. Каждый из РТ состоит из автономного вычислительного устройства (АВУ), усили-тельно-преобразующего устройства (УПУ), электромеханической РМ и линий передачи сигналов. Каждая РМ управляет углом поворота камеры ЖРД, установленной в карданном подвесе на раме, посредством шарнирнорычажного механизма.

Формирователем командного кода (ФКК) СУВТ ЖРД является бортовая цифровая вычислительная машина (БЦВМ). Посредством цифровой логики БЦВМ выдаёт заданные команды управления углом поворота камеры ЖРД в виде семиразрядного двоичного кода 8 1 , подаваемого в АВУ.

Для получения высокой точности позиционирования при скоростях вращения вала РМ ~50-60 °/с под нагрузкой необходимо, чтобы функции управления и цифровой коррекции сигналов осуществляло АВУ, работающее с собственным тактом квантования по времени, независимо по отношению к БЦВМ, а БЦВМ служило лишь источником входной информации. Так как частота сравнения кодов определяется тактом квантования по времени, то использование АВУ, работающего с частотой квантования в разы большей, чем тактовая частота выдачи БЦВМ управляющих сигналов, делает СУВТ подобной аналоговой системе, в которой сравнение сигналов происходит непрерывно [3].

АВУ включает в себя блок определения сигнала рассогласования, блок управления включением и остановом магнитоэлектрических двигателей (МЭД) РМ и представляет собой логическое устройство цифровой коррекции, работающее с собственной частотой квантования по времени, существенно большей, чем тактовая частота БЦВМ.

ФКК

а)

б)

Рис. 1. Система управления вектором тяги (СУВТ) жидкостного ракетного двигателя: а — конструкционнофункциональная схема СУВТ; б — декомпозиция СУВТ на функциональные элементы; ФКК — формирователь командного кода; ЖРД — жидкостный ракетный двигатель; РМ — рулевая машина; АВУ — автономное вычислительное устройство; УПУ — усилительно-преобразующее устройство; 8 — код рассогласования; 8 1 — командный код; 8 2 — код обратной связи; U — напряжение постоянного тока, подаваемое на РМ

АВУ выполняет следующие функции:

• •    в блоке определения сигнала рассогласования осуществляется преобразование кода Грея δ ₂ , поступающего от дискретных датчиков угла (ДДУ) обратной связи РМ, в двоичный код, сравнение его с кодом входного сигнала δ ₁ и определение кода их разности (рассогласования) δ ;

• •    в блоке управления включением и остановом МЭД РМ происходит формирование закона управления РМ путём сравнения кода рассогласования δ с заданной величиной кода переключения режима управления МЭД и с заданной величиной точности поддержания требуемого положения, при этом обеспечиваются необходимая длительность команд и время их выдачи.

УПУ представляет собой цифроаналоговый преобразователь, который преобразует сигнал рассогласования δ , поступающий от АВУ, в выходное напряжение необходимого уровня и полярности. Выходное постоянное напряжение от УПУ поступает на обмотки МЭД РМ, обеспечивая вращение выходного вала РМ.

В качестве исполнительных органов в рассматриваемой СУВТ ЖРД применены электромеханические РМ. Для повышения надёжности такие РМ выполняются с резервированием ответственных функциональных элементов. Конструкция таких РМ состоит из двух МЭД, кинематически соединённых с общим редуктором. В составе РМ имеются два контактных дискретных датчика угла (ДДУ) поворота выходного вала РМ, которые обеспечивают отрицательную обратную связь с АВУ. Семиразрядный ДДУ РМ имеет 128 дискретных положений выходного вала и 127 перемещений между ними. При совпадении кода положения выходного вала РМ, поступающего от ДДУ в АВУ, с кодом команды управления от ФКК (БЦВМ) АВУ выдаёт команду на выключение МЭД РМ и включение режима динамического торможения. В состав РМ входят также телеметрический потенциометр и путевые концевые контакты. Отличительной особенностью эксплуатации двухприводной электромеханической РМ является возможность её работы на одних участках с двумя функционирующими МЭД («горячий» резерв), а на других участках — только с одним, при этом второй МЭД находится в «холодном» резерве, но его вал продолжает вращаться синхронно первому. В составе СУВТ РМ работает в релейном режиме.

агрегирование нелинейной математической модели динамического режима работы СуВТ

В основу разработки нелинейной математической модели динамического режима работы СУВТ, а также методов расчёта её динамических характеристик были положены:

• •    математическая модель МЭД [4];

• •    математическая модель двухприводной электромеханической РМ ЖРД [5];

• •    принципы создания математических моделей электромеханических приводов и систем, изложенные в работах [6–11];

• •    численный метод решения систем нелинейных дифференциальных уравнений Рунге–Кутты 4-го порядка [12].

Принятые допущения:

• •    кинематическая связь выходного вала РМ с местом крепления тяги шарнирно-рычажного механизма к ЖРД представляется в виде дополнительной условной ступени редуктора РМ с эквивалентным моментом инерции рычага с присоединённой тягой шарнирно-рычажного механизма;

• •    связь между местом крепления тяги шарнирно-рычажного механизма и ЖРД полагается нежёсткой с общим коэффициентом крутильной упругости С , определяемым коэффициентами крутильной упругости мест крепления рычага к тяге С ₁ и тяги к ЖРД С ₂ [13]:

CC

C =      ^{1 2} .

C 1 + C 2

Для создания математической модели цифровой релейной электромеханической СУВТ в соответствии с принятыми допущениями были определены расчётным путём эквивалентный момент инерции дополнительной условной ступени редуктора РМ, а также общий коэффициент крутильной упругости С места крепления тяги шарнирнорычажного механизма к камере ЖРД. Масса элементов шарнирно-рычажного механизма определялась умножением объёма элемента на плотность материала, из которого изготовлен данный элемент.

При определении момента инерции дополнительной условной ступени редуктора РМ были приняты следующие допущения:

• •    рычаг шарнирно-рычажного механизма был представлен в виде поворотного стержня относительно оси вращения;

• •    тяга шарнирно-рычажного механизма была представлена в виде сосредоточенной массы (физического маятника), присоединённой к концу поворотного стержня посредством шарикового сферического подшипника на определённом расстоянии от центра масс тяги до оси вращения выходного вала РМ.

В соответствии с принятыми допущениями суммарный момент инерции дополнительной условной ступени редуктора был определён как сумма момента инерции стержня относительно оси вращения и момента инерции сосредоточенной массы (тяги) относительно оси вращения РМ J _∑ = J _с + J _т = 6·10^–4 кг·м².

Определение коэффициента крутильной упругости С места крепления тяги шарнирно-рычажного механизма к камере ЖРД было выполнено при допущении, что, поскольку тяга шарнирно-рычажного механизма представляет собой трубчатую конструкцию, в первом приближении можно воспользоваться известным коэффициентом линейной упругости основания силового гидроцилиндра электрогидрав-лической РМ ракетного блока С _о = 4,3·10³ кгс/см = 4,3·10⁶ Н/м [13].

Коэффициент крутильной упругости места крепления рычага к тяге С ₁ определяется плечом качания тяги рычагом h = 0,036 м, и тогда С ₁ = С _о h = = 4,3·10⁶·0,0^р36 = 0,1548·10⁶ Н/рад. ^{о р}

Коэффициент крутильной упругости места крепления тяги к ЖРД С ₂ определяется плечом качания камеры ЖРД h _к = 0,3 м, и тогда С ₂ = С _о h _к = 4,3·10⁶·0,3 = 1,29·10⁶ Н/рад.

Общий коэффициент крутильной упругости в соответствии с работой [13] определяется как

C =

^{C 1 C 2}

C, C

0,154·106·1,29·106

0,154·106 + 1,29·106

= 1,385·105 Н/рад.

Момент инерции подвижных частей РМ J, приведённый к валам магнито- электрического двигателя, согласно работе [5], определяется выражением

J = 2 J _д + J ₁ / i ₁ ² + J ₂ /( i ₁ ² i ² ₂ ) + J ₃ /( i ₁ ² i ² ₂ i ₃ ²) + J ₄ /( i ₁ ² i ² ₂ i ₃ ² i ₄ ²) + 2 J ₅ /( i ₁ ² i ² ₂ i ₃ ² i ₅ ²) + J ₆ /( i ₁ ² i ² ₂ i ₃ ² i ₆ ²),         (1)

где Jд — момент инерции ротора МЭД; J1, J2, J3, J4 — моменты инерции шестерни первой, второй, третьей и четвёртой ступеней редуктора соответственно; i1, i2, i3, i4 — передаточные числа первой, второй, третьей и четвёртой ступеней редуктора соответственно; J5 — момент инерции шестерни, соединяющей третью ступень редуктора с ДДУ с учётом момента инерции подвижных частей ДДУ; i5 — передаточное число пере- дачи от третьей ступени редуктора к валу ДДУ; J6 — момент инерции шестерни, соединяющей третью ступень редуктора с телеметрическим потенциометром (ТП) РМ, с учётом момента инерции подвижных частей ТП; i6 — передаточное число передачи от третьей ступени редуктора к валу ТП.

Полный момент сопротивления от элементов РМ М _с , приведённый к валам МЭД, определяется в этом случае как

Мс = Мс.э1+ Мс.э2 + 2Мк.к/(iрηр) + 2Мд.д.у/(iр1ηр) + Мт.п /(iр2ηр), где Мс.э1, Мс.э2 — моменты сухого трения в МЭД; Мк.к — момент сухого трения от концевых контактов; iр — передаточное число редуктора РМ, iр = i1i2i3i4; iр1 — передаточное число передачи от валов МЭД к валам ДДУ с учётом встроенного в ДДУ редуктора, iр1 = i1i2i3i5; iр2 — передаточное число передачи от валов МЭД к валу ТП, iр2 = i1i2i3i6; ηр — КПД редуктора РМ и других передач от валов МЭД к валу ТП и к валам ДДУ, ηр = η1η2η3η4, где η1 ... η4 — КПД каждой ступени; Мд.д.у и Мт.п. — моменты, приведённые к валам ДДУ и ТП соответственно.

Тогда общий момент инерции подвижных частей СУВТ J _о , приведённый к валам МЭД РМ, с учётом момента инерции дополнительной условной ступени редуктора РМ с эквивалентным моментом инерции рычага с присоединённой тягой шарнирно-рычажного механизма определяется выражением:

J0 = 2Jд + J1/i12 + J2/(i12 i22) + J3/(i12 i22 i32) + J4/(i12 i22 i32 i42) + 2J5/(i12 i22 i32 i52) + J6/(i12 i22 i32 i62) + J∑ /(i12 i22 i32 i42 i72), где J∑ — момент инерции дополнительной условной ступени редуктора РМ с эквивалентным моментом инерции рычага с присоединённой тягой шарнирно-рычажного механизма; i7 — передаточное число дополнительной условной ступени редуктора РМ.

Общий КПД редуктора РМ с дополнительной условной ступенью определяется как

ηо = η1η2η3η4η7, где η7 — КПД дополнительной условной ступени редуктора.

Математическая модель динамического режима работы цифровой релейной электромеханической СуВТ

Математическая модель СУВТ с простейшим релейным алгоритмом управления РМ, согласно работам [4, 5], включает в себя следующие уравнения:

dI 1 = b U – bI – bω; dt       1        2 1      3 (2) dI dt2 = b1U – b4I2 – b5ω; (3) dϕ = ω; dt (4) dω dt = b6I1 + b7I2 – b8Mcsign(ω) – – b9(1/iоηо)[(ϕ/iо) – β]; (5) dβ dt = Ω; (6) dΩ ∑M dt = Jk ; (7) δ = δ1 – δ2; (8) α = ϕ; ip (9) δ1 = int[(127/αmax)αт]; (10) δ2 = int[(127/αmax)(ϕ/iр)·57,295°]; (11) при |δ| > 1 → U = Uн sign(δ);(12)

при |δ| ≤ 1 → U = 0;(13)

∑I = I1 + I2,(14)

где b ₁ ... b ₉ — постоянные коэффициенты,

• b ₁ = 1/ L ; b ₂ = R ₁ / L ; b ₃ = K _э1 / L ;

• b ₄ = R ₂ / L ; b ₅ = K _э2 / L ; b ₆ = K _м1 / J ;

• b 7 = K м2 / J ; b 8 =1/ J ; b 9 = С / J о ,

здесь L — индуктивность обмоток электрической цепи МЭД; R ₁ и R ₂ — активное сопротивление электрической цепи первого и второго МЭД соответственно; U — напряжение питания, подаваемое на МЭД; K _э1 и K _э2 — коэффициенты электромагнитной скоростной связи первого и второго МЭД соответственно; I ₁ и I ₂ — ток, потребляемый первым и вторым МЭД соответственно; ω — угловая скорость вращения валов обоих МЭД, кинематически соединённых с общим редуктором; ϕ — угол поворота валов обоих МЭД; K _м1 и K _м2 — коэффициенты моментной характеристики первого и второго МЭД соответственно; J — момент инерции вращающихся частей РМ, приведённый к валам МЭД, определяемый по выражению (1); i _о — передаточное число передачи от валов МЭД к месту крепления тяги шарнирно-рычажного механизма к ЖРД, i _о = i ₁ i ₂ i ₃ i ₄ i ₇ ; η _о — общий КПД редуктора РМ с учётом КПД η ₇ дополнительной условной ступени от рычага с присоединённой тягой шарнирно-рычажного механизма, η _о = η ₁ η ₂ η ₃ η ₄ η ₇ ; β — угол поворота камеры ЖРД в данной плоскости качания; Ω — угловая скорость поворота камеры ЖРД; α — угол поворота выходного вала редуктора РМ; J _к — момент инерции камеры ЖРД; δ ₁ — код командного сигнала; δ ₂ — код текущего положения вала РМ; δ — код рассогласования; α _max — максимальный угол поворота выходного вала РМ; α _т — требуемый угол поворота вала РМ; U _н — номинальное напряжение питания МЭД РМ; ∑ I — суммарный ток, потребляемый МЭД РМ; ∑ М — сумма моментов, действующих на камеру ЖРД,

C ( ф / i о - в ) - M с.т.к sign( Q ) - K м_ р - М п.к при Я * 0;

S M = <

^{C (} ф / i о ^{- в) -} M с.т.к sign ^{C (} ф / i о

- в ) - К мпж в - ^М п.к ] - K м.п.к

в - ^М пж

^п Ри Я = 0 и I С ⁽ ф / i о ^{- в) -} К м.п.к.

в - ^М nJ >  M с.тж ;

0 при Я = 0 и C ( ф / i о - в ) - К м.п.к в

– Мп.к| ≤ Mс.т.к, здесь Mс.т.к — момент сухого трения камеры ЖРД; Kм.п.к — коэффициент позиционного момента камеры ЖРД от упругости сильфонных трубопроводов и дисбаланса камеры; Mп.к — постоянный момент, действующий на камеру ЖРД от асимметрии тяги.

Уравнения (2) – (14) с учётом выражения (15) образуют нелинейную математическую модель цифровой релейной электромеханической СУВТ ЖРД для варианта её эксплуатации с двумя функционирующими МЭД РМ, пригодную для решения численными методами. Для моделирования варианта эксплуатации СУВТ с одним функционирующим МЭД РМ достаточно приравнять нулю коэффициент моментной характеристики второго МЭД, т. е. K _м2 = 0, а выходным параметром математической модели считать только ток I ₁ , потребляемый первым МЭД РМ, а также при вычислении суммарного тока, потребляемого МЭД РМ, значение тока второго МЭД I ₂ полагать равным нулю. Этот приём позволит избежать возникновения в процессе моделирования работы СУВТ включения режима динамического торможения второго МЭД РМ.

апробация разработанной нелинейной математической модели динамического режима работы цифровой релейной электромеханической СуВТ жрд

Апробацию разработанной нелинейной математической модели динамического режима работы цифровой релейной электромеханической СУВТ ЖРД удобно провести путём расчёта переходной характеристики СУВТ для прямого и обратного направлений углового перемещения камеры ЖРД.

Интегрирование нелинейных дифференциальных уравнений математической модели РМ осуществлялось в процессе проведения вычислительных экспериментов методом Рунге–Кутты четвёртого порядка [12] в среде Free Pascal [14].

Поскольку РМ не имеет внутреннего предохранителя, а угол поворота вала РМ из среднего положения до упоров составляет ±27,1 ° , для исключения постановки вала РМ на упор значение требуемого угла поворота вала РМ а было принято следующим: а т = ±20 ° . т

На рис. 2 представлена переходная характеристика угла поворота выходного вала РМ СУВТ в зависимости от времени при ступенчатом входном воздействии в виде требуемого поворота выходного вала РМ а т = ±20 ° (см. целевую ступенчатую функцию на графике) для режимов работы с двумя и с одним МЭД РМ. На этом же рисунке представлена экспериментальная переходная характеристика, полученная при испытаниях в составе ЖРД, для режима работы с двумя МЭД.

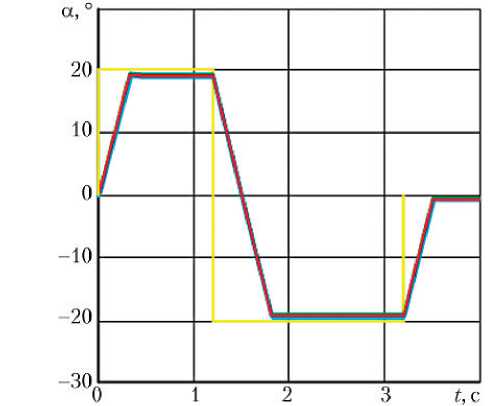
Рис. 2. Переходные характеристики угла поворота выходного вала РМ СУВТ для режима работы РМ:    — с двумя МЭД (расчёт);   — с одним МЭД (расчёт); --- — с двумя МЭД (эксперимент);

--целевая ступенчатая функция

Как видно из графиков рис. 2, экспериментальная и расчётная характеристики практически совпадают. Переходные характеристики угла поворота выходного вала РМ для режимов работы РМ СУВТ с двумя и с одним МЭД тоже практически совпадают, что подтверждает возможность работы РМ

СУВТ на отдельных участках циклограммы полёта изделия в режиме с одним МЭД. Также на графиках рис. 2 видно, что слежение осуществляется с некоторой ошибкой как в одну, так и в другую сторону. При прямом ходе ошибка составляет 3,7%, а при обратном — 1,85% от диапазона регулирования, что объясняется влиянием постоянно действующего момента и момента сухого трения камеры ЖРД.

На рис. 3 представлены расчётные переходные характеристики суммарного потребляемого тока РМ СУВТ в зависимости от времени при ступенчатом входном воздействии в виде требуемого угла поворота выходного вала РМ а т = ±20 ° для режимов работы с двумя и с одним МЭД РМ.

Графики рис. 3 показывают, что МЭД в процессе функционирования РМ работают практически в режиме пусковых токов. Это является особенностью работы цифровой релейной электромеханической СУВТ.

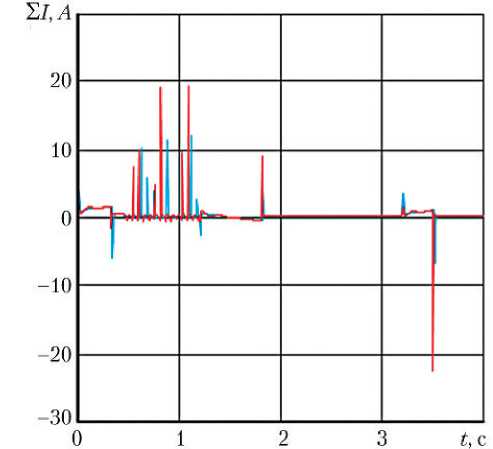
Рис. 3. Переходные характеристики суммарного потребляемого тока РМ СУВТ для режима работы:

--- — с двумя МЭД; --- — с одним МЭД

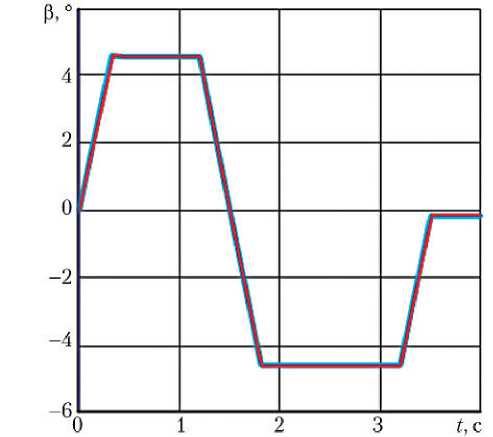
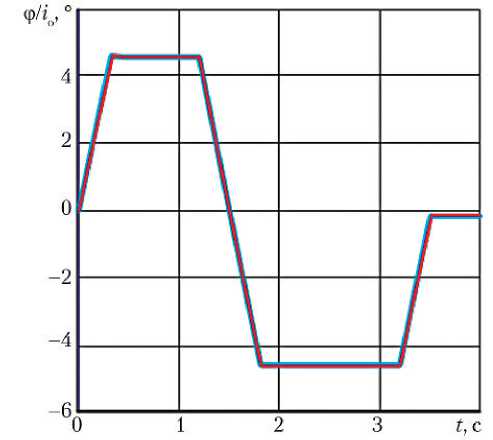
На рис. 4 представлены расчётные переходные характеристики угла поворота камеры ЖРД СУВТ в и угла поворота места крепления тяги шарнирно-рычажного механизма к ЖРД ф / i о в зависимости от времени для режимов работы с двумя и с одним МЭД РМ.

Как и в случае переходных характеристик угла поворота выходного вала РМ в зависимости от времени для режимов работы РМ с двумя и с одним МЭД, переходные характеристики угла поворота камеры ЖРД СУВТ и угла поворота места крепления тяги шарнирно-рычажного механизма к ЖРД в зависимости от времени также совпадают. Кроме этого, наблюдается практически полное совпадение переходных характеристик угла поворота камеры ЖРД и угла поворота места крепления тяги шарнирно-рычажного механизма к ЖРД в зависимости от времени, что подтверждает высокую жёсткость силовой проводки шарнирно-рычажного механизма при полученном общем коэффициенте крутильной упругости С.

а)

б)

Рис. 4. Переходные характеристики угла поворота камеры ЖРД СУВТ (а) и угла поворота места крепления тяги шарнирно-рычажного механизма к ЖРД (б) для режима работы РМ: --- — с двумя

МЭД; _- — с одним МЭД

Жёсткостью силовой проводки в этом случае можно было бы пренебречь, однако для соблюдения всех режимов сухого трения в нагрузке представляется целесообразным оставить математическую модель в представленном виде. Кроме этого, наличие в математической модели коэффициента крутильной упругости С позволит при дальнейших исследованиях сравнить резонансы экспериментальной и расчётной частотных характеристик и провести точную идентификацию некоторых параметров камеры ЖРД.

заключение

В итоге проведённых разработок получены следующие основные результаты:

• •    выполнена декомпозиция цифровой релейной СУВТ ЖРД на составляющие функциональные элементы;

• •    разработаны уравнения для момента инерции и КПД СУВТ;

• •    агрегирована нелинейная математическая модель динамики цифровой релейной СУВТ ЖРД для вариантов её эксплуатации с функционированием одного из МЭД РМ и нахождением второго МЭД РМ в «холодном» резерве, а также для варианта её эксплуатации с функционированием обоих МЭД РМ («горячий» резерв);

• •    выполнена апробация нелинейной математической модели динамического режима работы цифровой релейной электромеханической СУВТ ЖРД для режимов работы с двумя и с одним МЭД;

• •    определено, что в процессе функционирования РМ её МЭД работают практически в режиме пусковых токов, и это является особенностью работы цифровой релейной электромеханической СУВТ;

• •    в результате математического моделирования и расчёта переходных характеристик СУВТ определено, что силовая проводка шарнирно-рычажного механизма ЖРД является достаточно жёсткой и не вызывает колебательных режимов работы СУВТ.

Рисунки в статье созданы авторами.