Математическая модель ЦОВ с учетом повторных вызовов

Вопросу технологии обслуживания вызовов посвящены работы многих отечественных и зарубежных авторов. Например, в [1] рассматривается назначение, аппаратно-программный комплекс, алгоритм функционирования центров обслуживания вызовов (ЦОВ). В работе [2] приведен сравнительный анализ моделей ЦОВ и сделаны выводы относительно их практического применения. В работе [3] рассматриваются функциональные особенности ЦОВ, организация очередей и маршрутизация вызовов, а также модели обслуживания и обработки информации.

Отличие предлагаемой математической модели (ММ) от известных заключается в том, что в отдельные состояния выделены внутрисистемные процессы обслуживания вызовов. Выделен процесс организации очереди первичных и повторных вызовов, поскольку они имеют разную интенсивность поступления и требуют обслуживания операторами разной квалификационной группы. При передаче вызова с одного операторского уровня на другой также создается очередь вызовов, но уже между операторскими группами. В связи с этим и процесс обслуживания вызовов из разных очередей также выделен в отдельное состояние.

В предлагаемой ММ учитывается и человеческий фактор, например, степень нетерпе- ливости абонента, степень удовлетворенности обслуживанием и т.п. Примечательно также и то, что желаемое время ответа (Service Time, sec.) для всех категорий вызовов (LOW ARPU, MIDDLE ARPU, HIGH ARPU, KEY) одинаково и никак не учитывает повторные вызовы. Перечисленные особенности функционирования ЦОВ непосредственно влияют на такой общий показатель производительности, как обслуживание на заданном уровне (Service Level, SL), выраженный в процентах. Предлагаемая ММ и полученные новые формулы расчета позволяют учесть эти особенности функционирования ЦОВ и уточнить значения основных вероятностно-временных характеристик его производительности по статистическим данным системы мониторинга.

Как правило, для оценки эффективности производительности ЦОВ используют понятия «количественные и качественные показатели производительности». К количественным показателям относятся показатели, вычисляемые по статистическим данным, собираемым системой мониторинга производительности ЦОВ. Количественные показатели оцениваются в абсолютных величинах. Вычисление этих показателей связано с организацией процесса обслуживания вызовов. Для наиболее полного представления о производительности ЦОВ осуществляется сбор данных на уровне операторских групп и очередей, на уровне операторов, на уровне то- чек входа в систему, на уровне соединительных линий. У разных производителей бывают разные наборы отчетов, но эти уровни являются общими для большинства из них.

Точка входа в операторский центр чаще всего представляет собой виртуальный внутренний номер коммутатора, физически не закрепленный ни за каким оборудованием. Так как она является обычным внутренним номером коммутатора, то и доступ к ней может осуществляться практически любым способом, предусмотренным для внутренних номеров. Очередей на уровне точки входа в операторский центр нет, они образуются на уровне операторских групп. Тем не менее отчеты на уровне точек входа очень важны, так как позволяют оценить все время, потраченное на обслуживание вызова, включая и то, когда абонент слышит входное приветствие, а также определить, сколько вызовов теряется еще во время воспроизведения приветствия. Отчеты включают ряд комплексных параметров, которые можно использовать для оценки и расчета производительности и качества обслуживания вызовов ЦОВ.

Однако только по этим показателям оценить производительность ЦОВ в части результата его работы относительно клиентов достаточно сложно. Поэтому вводится понятие качественных показателей производительности [4; 7-10]. Качественные показатели характеризуют уровень предоставления информации и степень удовлетворенности клиентов работой ЦОВ. Таким образом, их значения напрямую могут влиять на алгоритмическую организацию технологических процессов внутри ЦОВ.

К основным качественным показателям относятся, например, индекс потребительской удовлетворенности (Customer Satisfaction Index, CSI), который измеряется в баллах, а также интегральный показатель «метод маркетинговых исследований» (Mystery shopper index, MSI), который предполагает оценку качества обслуживания с помощью специалистов, выступающих в роли «Таинственных Покупателей» и измеряется в процентах. Но наиболее действенным является показатель FCR (First Call Resolution) – процент вызовов, при которых получен ответ на вопрос с первого раза. Показатель FCR управляет степенью удовлетворенности клиентов.

FCR делит все обращения на две категории: первичные и повторные. Расчет показателя производится следующим образом: FCR = 100 – по-вторные/всего взаимодействий *100%, где «всего взаимодействий» – это отработанные вызовы, с которыми был завершен разговор без перевода на другие направления. Признаком повторного обращения являются повторы ранее созданного взаимодействия с оператором, отличающиеся от текущего не более, чем на 24 ч с любой темой от того же клиента. Например, завершив диалог, клиент перезванивает в ЦОВ в течение 24 ч, и, соответственно, создается взаимодействие, которое будет считаться повторным. В этом случае не имеет значения, сколько раз за 24 ч клиент обратится в ЦОВ еще раз, факт повторного обращения уже есть.

Клиент может многократно обращаться в ЦОВ, при этом его вопрос никак не могут решить. Важность клиента для компании может быть разной, то есть многократно могут обращаться как VIP-клиенты, так и менее приоритетные, и с каждым последующим вызовом степень удовлетворенности и лояльности клиентов снижается. Причины повторных обращений бывают разные, но наиболее часто встречаются следующие:

• -    отсутствие информации;

• -    отсутствие полномочий для решения проблемы;

• -    неверное распределение вызовов (маршрутизация);

• -    долгое удержание на hold (длина очереди);

• -    производительность и т.п.

Таким образом, для повышения эффективности функционирования ЦОВ необходимо уменьшить число повторных обращений клиентов. Задача решается созданием экспертного уровня, расчетом прогнозируемого времени ожидания, пересмотром бизнес-процессов, утверждением методики сбора и обработки статистических данных. Однако и эти меры бывают недостаточны. Например, возникают ситуации, когда абонент осуществляет вызов не в первый раз за сутки и знает, что ему нужно связаться сразу с экспертами, при этом он не может попасть в очередь к операторам второй линии, минуя первую линию. Соответственно, число очередей, в которых приходится ожидать абоненту, увеличивается вдвое, а если он звонит уже в третий или в четвертый раз, это приносит существенные неудобства. Кроме этого, при переводе с одного уровня на другой абоненты нередко «срываются», а значит, им приходится перезванивать.

Таким образом, при выборе метода маршрутизации вызова и, соответственно, способа обслуживания клиента необходимо отслеживать и учитывать повторные обращения.

Математическая модель и расчет показателей производительности ЦОВ

На рис. 1 представлена ММ, предназначенная для оценки влияния повторных вызовов на производительность ЦОВ. Модель разработана в соответствии с обобщенным алгоритмом функционирования, опубликованным в [5], где описан процесс обслуживания клиентских обращений в условиях существования повторных вызовов, вычисления расчетного и прогнозируемого времени ожидания и коэффициента уровня обслуживания (Service Objective, SO). Основу алгоритма составляет прогностический метод маршрутизации вызовов.

Модель позволяет получить аналитические формулы для расчета основных качественных показателей функционирования ЦОВ. В ММ выделены процесс поступления первичного и повторного вызовов на уровне точки доступа, процесс обработки двух видов вызовов операторами первого и второго уровней обслуживания, учтены вероятности неудовлетворенности обслуживанием на каждом уровне. Поскольку очереди, образующиеся первичными и повторными вызовами при обслуживании операторами первого и второго уровня, относятся к разным алгоритмическим процессам, они также выделены в отдельные состояния.

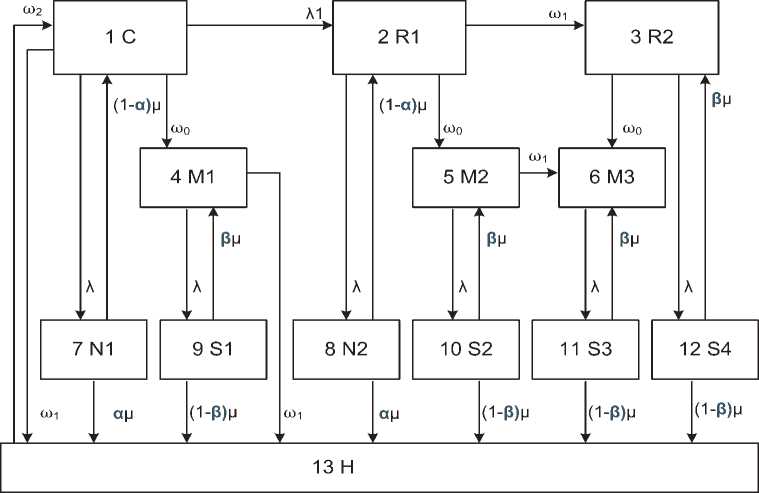
Рис. 1. Схема ММ функционирования ЦОВ с учетом повторных вызовов

В ММ приняты следующие обозначения: С – точка входа в систему ЦОВ; R1 – точка входа повторного вызова к оператору первого уровня; R2 – точка входа повторного вызова к оператору второго уровня с учетом того, что оператор может входить в операторскую группу первого и второго уровня одновременно; N1, N2 – состояния обслуживания первичного и повторного вызовов вне очереди соответственно; M1, M2, М3 – состояния, в которых абонент ожидает ответа оператора, М1 – очередь на обслуживание операторской группой первого уровня, создаваемая первичными вызовами, М2 – очередь на обслуживание операторской группой второго уровня, создаваемая повторными вызовами, М3 – очередь на обслуживание операторами второго уровня, создаваемая повторными вызовами абонентами, неудовлетворенными обслужива- нием операторами первого уровня; S1 – состояние обслуживания первичного вызова операторами первого уровня; S2 – состояние обслуживания повторного вызова операторами первого уровня, вызов поступает в порядке очереди, расчетное и прогнозируемое время ожидания меньше порогового значения; S3 – состояние обслуживания повторного вызова от абонентов, неудовлетворенных обслуживанием оператором первого уровня и второго уровня, вызов поступает из очереди, обозначенной в ММ как состояния М2 и М3; S4 - состояние обслуживания вызова от абонентов, неудовлетворенных обслуживанием операторами первого уровня вне очереди (по приоритету), Н – состояние завершенного обслуживания.

Переходы между состояниями обозначены: Я – интенсивность поступления первичного вы- зова; 2t – интенсивность поступления повторного вызова; 6УО – интенсивность поступления вызовов в очередь; CDX – интенсивность потерь вызовов оператором первого уровня; йу – интенсивность освобождения оператора; а – вероятность того, что абонент не будет удовлетворен обслуживанием операторской группой первого уровня; Р – вероятность того, что вызов, поступивший из очереди, также будет обслужен неудовлетворительно.

Для вывода формул был использован метод анализа вероятностных систем [6]. Значение средних времен нахождения вызова в точке доступа и в состоянии обслуживания повторного вызова определяются состояниями С и R1, обозначены как ^ci^H t_RX соответственно. Значение среднего времени пребывания абонента в очереди ожидания ответа оператора определяется состояниями М1, М2, М3, обозначено как ^М ^М\^М2^МЗ" Аналогично значение среднего числа вызовов, приходящееся на одного оператора, определяется состояниями обслуживания, обозначенными буквами N и S в ММ. Среднее число вызовов, приходящееся на одного оператора, будет состоять из трех составляющих: /71 соответствует состояниям N1 и S1, ГЦ соответствует состояниям N2 и S2, п₃ соответствует состояниям S3 и S4. Для удобства вычислений в расчетных формулах приняты следующие обозначения:

, 2, + аХ ,        2(1 - Р)

а = 1 + —---- ; Ь = со₀* ———;

й)^ + 69^              СО^ + О)^

(У.+2(1-1)  , 1 ЬХ с = —----—— ; d = I +-----.

со₀ + бУ,                бУ₀ + бУ,

Тогда t =<о0 +^i. бУ2 (бУ0 + бУ] + 2] + 6z2)

2,                    бУр

'Л1 —   , ‘ci ’ lM\ ,      ,1 ’ d            ас^й)0 + бУ,)

_     2,бУ0.

'М2 — acdVG)0 + бУх)

_t _ Х_х to_x (2(1 - рХс + 6У_О2) + 6У_О) .

мз b acdX(l - РХго0 + coY )

+(1 + 2(1-/?)).      2,2(1 +2(1-Д)) .

П^ —----------------5 ^2 — ’ ас         *acd

• 2,    бУ, (2(1 - РХс + бу, (1 + бу,))) /73 —                      -.

аса

Вероятность того, что вызов не будет обслужен оператором (вероятность потерь), определяется по формуле р _ (opcopXd + ^ + d^cd^yic + cop^ + coP + l

• ^р copb'pd + Р)(с +юр)+ dXco_x(y(c + ct)₀X) +0)^ + 1

где у = Д1-№- В результате проведенных выкладок получены аналитические формулы для определения значений среднего времени нахождения вызова в точке входа при поступлении первичного и повторного вызовов при прослушивании абонентом голосового меню (состояния C и R1 в MM), среднего времени нахождения первичного и повторного вызовов в очереди (состояния М1, М2, М3). При расчете учитывалось то обстоятельство, что вызов может переключаться от одного оператора к другому, а значит, переходить из одной очереди в другую, не покидая систему.

На рис. 2 показан график зависимости вероятности потерь вызовов от интенсивности отказа в обслуживании из-за нетерпеливости абонентов, недопустимого значения расчетного и прогнозируемого времени ожидания.

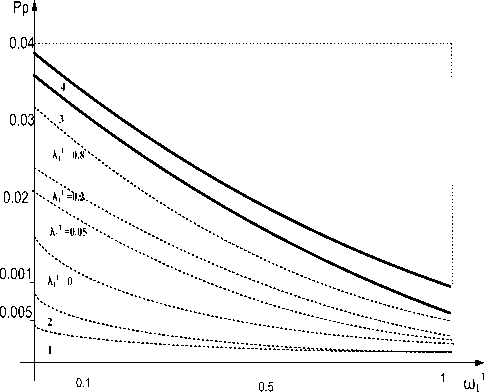
Рис. 2. Зависимость вероятности потерь от интенсивности отказа в обслуживании

Зависимости приведены при разных значениях интенсивности поступления повторных вызовов 2], которая выражена относительным параметром Д. Параметр показывает, во сколько раз интенсивность поступления повторных вызовов превышает общую интенсивность потерь вызовов, включая и уход абонента из очереди при превышении расчетного и прогнозируемого значения времени ожидания: Х\ =2] /(бУ₀ + бУ]).

Для наглядности на графике интенсивность потерь вызова также выражена относительным параметром, показывающим долю потерянных вызовов к общему числу поступивших, в том числе и повторно, вызовов:

Анализ полученных результатов показывает, что значение вероятности потерь существенно зависит от интенсивности поступления повторных вызовов при общей интенсивности отказов со₀ + со, = 0,001 ч^-1.

Заключение

В статье приведена ММ обобщенного алгоритма функционирования ЦОВ с учетом повторных вызовов и проведены исследования основных вероятностно-временных параметров функционирования ЦОВ.

Получены аналитические формулы для расчета среднего числа вызовов, приходящиеся на одного оператора. Формулы позволяют оценить загрузку операторов первого и второго (экспертного) уровня первичными и повторными вызовами отдельно. Это, в свою очередь, дает возможно сть оценить эффективность работы ЦОВ с учетом повторных вызовов, скорректировать показатель FCR и произвести перерасчет числа операторов на одного супервайзера.

Получена формула расчета вероятности потерь вызовов, в которой учтены все вышеперечисленные особенности функционирования ЦОВ. Выведены графики зависимости вероятности потерь вызовов от интенсивности отказа в обслуживании. Количественные значения переменных, используемых в предлагаемых формулах расчета, определяются по статистическим данным системы мониторинга ЦОВ, и входящей в эту систему системой отчетности и управления (Call Management System, CMS).

Приведенные аналитические зависимости связывают множество исходных данных системы контроля и управления с вероятностновременными параметрами, характеризующими производительность ЦОВ. Они отражены в формулах, позволяющих оценить производительность системы при стратегическом планировании и разработки бизнес-проектов существующих и проектируемых ЦОВ, а также для организации обучения кадрового состава, расчета общего числа операторов первого и экспертного уровней с целью повышения эффективности их работы.