Математическая модель динамики периферийного стыковочного механизма с накоплением кинетической энергии сближения космических аппаратов
Автор: Яскевич Андрей Владимирович
Журнал: Космическая техника и технологии @ktt-energia
Рубрика: Динамика, баллистика, управление движением летательных аппаратов
Статья в выпуске: 3 (26), 2019 года.
Бесплатный доступ
Новый периферийный стыковочный механизм входит в состав стыковочного агрегата, проект которого соответствует международному стандарту систем стыковки (IDSS). Кинематика механизма основана на платформе Гью-Стюарта. Для преобразования энергии сближения космических аппаратов используются пружинные механизмы, но традиционное демпфирование заменено накоплением энергии, поэтому конструкция содержит новые устройства. Математическая модель динамики стыковочного механизма, описанная в данной работе, учитывает все его основные особенности - кинематику, инерцию и формирование внутренних активных сил отдельными устройствами. Вместе с уравнениями динамики космических аппаратов и алгоритмами анализа контактного взаимодействия стыковочных агрегатов она входит в математическую модель стыковки, которая используется для анализа кинематики и динамики этого процесса от первого контакта до завершения стягивания.
Космический аппарат, стыковочный механизм, уравнения динамики
Короткий адрес: https://sciup.org/143172148
IDR: 143172148 | УДК: 629.78.028.24:004.94 | DOI: 10.33950/spacetech-2308-7625-2019-3-98-108
Текст научной статьи Математическая модель динамики периферийного стыковочного механизма с накоплением кинетической энергии сближения космических аппаратов
ЯСКЕВИЧ А.В.
Устройство стягивания нового периферийного стыковочного механизма
В работе [1] описана кинематика нового периферийного стыковочного механизма (СтМ), в котором вместо традиционного демпфирования энергии сближения космических аппаратов (КА) реализуется принцип ее накопления в специальных устройствах [2], состоящих из пружинных механизмов (ПМ) вращения и управляемых обгонных муфт (УОМ). Эти устройства установлены на корпусах штанг платформы СтМ и связаны передачами с шарико-винтовыми преобразователями (ШВП) поступательного перемещения штоков. Штоки каждой штанги СтМ имеют три фиксированных положения:
-
• полностью втянутое (ПМ максимально сжаты), переднее (ПП);
-
• полностью выдвинутое (силы сопротивления, создаваемые ПМ, минимальны);
-
• некоторое промежуточное — исходное (ИП) перед стыковкой.
При нахождении штока каждой штанги в ИП контактное устройство, связанное передачей с ШВП, формирует для блока управления сигнал о наличии такого положения, а отдача ПМ блокируется УОМ. В процессе стыковки, вследствие движения стыковочного кольца из-за контактов стыковочных агрегатов, сигнал о нахождении в ИП штока какой-либо из штанг теряется. В ответ на это блок управления и УОМ снимают блокировку ПМ всех штанг, и стыковочное кольцо выдвигается навстречу пассивному агрегату для ускорения сцепки. После ее достижения блокировка всех ПМ опять включается, и они начинают накапливать энергию сближения КА.
Втягивание СтМ, т. е. стягивание стыковочных агрегатов и КА, осуществляется специальным устройством с помощью трех тросов, одни концы которых закреплены на стыковочном кольце, а другие — на барабанах, установленных на основании механизма и приводимых в движение одним приводом. Кинематическая схема этого устройства приведена на рис. 1. Конструктивно с барабанами объединены малогабаритные силовые редукторы, которые обеспечивают необходимую величину силы натяжения тросов. От привода к ним передается незначительный момент. Для этого могут использоваться, например, гибкие валы [3].
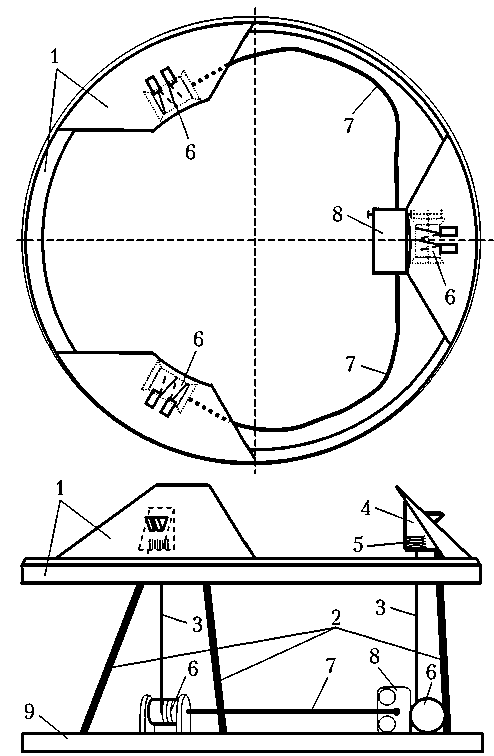
Рис. 1. Кинематическая схема устройства стягивания стыковочного механизма: 1 — стыковочное кольцо с направляющими выступами; 2 — штанги (условно); 3 — тросы; 4 — корпуса механизмов защелок; 5 — пружины компенсации разности длин тросов; 6 — барабаны намотки тросов с силовыми редукторами и кулачками; 7 — гибкие валы; 8 — привод; 9 — основание стыковочного механизма
Выходные валы силовых редукторов и валы барабанов связаны через пружины, допускающие разность их углового хода. Их совместное вращение осуществляется при контакте соответствующих кулачков. При отсутствии силы натяжения какого-либо троса пружина в его барабане отводит кулачок барабана от кулачка редуктора. Данная конструктивная особенность используется для выравнивания СтМ. Подробнее функционирование устройства стягивания рассмотрено ниже при описании его модели.
Уравнения динамики платформы периферийного СтМ
Математическая модель процесса стыковки включает в себя уравнения динамики стыкуемых КА, алгоритмы анализа контактного взаимодействия стыковочных агрегатов, уравнения динамики СтМ. Вследствие кратковременности процесса, КА представляются твердыми или деформируемыми свободными телами, движущимися без учета их орбитального движения под действием контактных, инерционных и управляемых сил и моментов. Их уравнения динамики описаны в статье [4]. Алгоритмы контактного взаимодействия стыковочных агрегатов рассмотрены в работах [5, 6].
Стыковочный механизм активного агрегата обладает значительно меньшей инерцией, чем стыкуемые КА, но создаваемые им силы и моменты могут быть на порядок больше, чем у реактивной системы управления КА. Поэтому при математическом моделировании необходимо корректно определять относительные перемещения его звеньев. Для СтМ, имеющих до шести собственных степеней свободы, это обеспечивается численным интегрированием их дифференциальных уравнений динамики (УД). С учетом различной инерции СтМ и КА их движение описывается отдельными уравнениями. При этом силы и моменты, действующие в основании СтМ, входят в УД активного КА. Обратное влияние проявляется через создаваемое активным КА переносное движение основания механизма.
Новый периферийный СтМ представляет собой параллельный манипулятор в виде платформы Гью–Стьюарта [7, 8], т. е. является механической системой твердых тел с шестью кинематическими контурами. Его динамика определяется инерцией всех ее звеньев, их относительными перемещениями и скоростями в шарнирах. Поэтому при разработке его модели сначала условно размыкаются все контуры, и структура такой преобразованной механической системы становится древовидной. Для нее составляются УД относительно всех ускорений относительного движения в шарнирах. Совместно с ними учитываются ограничения на движение, обусловленные кинематическими контурами и описываемые соответствующими уравнениями связей относительно шарнирных координат, скоростей и ускорений. Способы такого совместного решения могут быть различными, а размерность совместной системы дифференциально-алгебраических уравнений может значительно превышать число степеней свободы исходной механической системы. Особенностью СтМ является отсутствие сингулярных конфигураций, т. е. существование решения контурных уравнений связей во всем его рабочем пространстве. Такое решение может быть использовано для снижения размерности УД преобразованной механической системы до числа степеней свободы СтМ. Для этого УД должны быть записаны в замкнутой форме, т. е. в явном виде относительно полного вектора шарнирных ускорений. Для простой кинематической цепи коэффициенты таких уравнений наиболее эффективно вычисляются при использовании рекуррентного алгоритма [9, 10]. В работе [11] описана его модификация для древовидной преобразованной механической системы. Она дополнена алгоритмом расчета сил и моментов в основании, так как замкнутая форма УД, в отличие от рекуррентной, не обеспечивает возможность такого вычисления.
Существование решения уравнений контурных связей позволяет применить метод разделения шарнирных ускорений на зависимые и независимые [12] и использовать его для редукции УД преобразованной древовидной механической системы. Развитие этого метода с учетом особенностей кинематики СтМ рассмотрено в работе [13]. В результате УД платформы СтМ записываются в замкнутой форме, в данном случае — наиболее эффективной по критерию объема вычислений
A(q)q.. = b( q, q.) + QF, где q, q, q — (nxl) — векторы обобщенных (независимых) координат, скоростей и ускорений СтМ; A(q) - (nxn) — обобщенная матрица инерции; b(q, q) - (nx1) — вектор обобщенных инерционных сил; QF — (ПXl) — вектор обобщенных внешних и внутренних активных сил; n — число степеней свободы механизма.
Внутренние активные силы, создаваемые СтМ, наряду с внешними, контактными, определяют динамику стыковки. В новом периферийном СтМ они создаются принципиально новыми устройствами — накопления энергии и стягивания. Ниже их математические модели рассматриваются более подробно.
Расчет сил сопротивления, создаваемых устройствами накопления энергии
Устройство накопления энергии каждой штанги состоит из ПМ и УОМ, которая блокирует или разрешает его отдачу. УОМ расположена в корне кинематической цепи, начинающейся в месте крепления верхнего шарнира штанги к стыковочному кольцу. Поэтому блокировка вала ПМ не предотвращает деформацию этой цепи. Модель устройства накопления энергии описывает изменение создаваемой ПМ силы сопротивления перемещению штока в зависимости от состояния УОМ. При этом учитываются деформация кинематической цепи и потери механической энергии, обусловленные сухим и вязким трением. Первое из них обусловлено, в основном, лентой ПМ, второе — передачами вращения в кинематической цепи штанги. Использование идеализированной, упрощенной модели сухого трения в виде f FR ( t ) = –sign( v ( t )) F FR , где v — скорость, а F FR — постоянная сила трения, при численном интегрировании УД приводит к высокочастотному вычислительному шуму, обусловленному изменениями знака скорости при пренебрежимо малой ее амплитуде. При значительных силах, создаваемых ПМ, такой шум снижает корректность математической модели, поэтому по аналогии с работой [14] модель устройства накопления энергии описывается характеристикой гистерезиса, величина которого (разность амплитуд прямого и обратного ходов, запаздывание по фазе движения) определяется главным образом экспериментально, иногда в результате экспертной оценки.
Положительная деформация соответствует уменьшению хода штока и сжатию ПМ, отрицательная — растяжению кинематической цепи штанги при нахождении ее штока в ПП или при включенной блокировке отдачи ПМ. Для описания силы сопротивления ходу штока штанги используется кусочно-линейная модель. В соответствии с ней, в любой момент времени t сила f S ( t ) сопротивления вычисляется по известной текущей деформации d ( t ) как f S ( t ) = f B ( t ) + k ( t )( d ( t ) – d B ( t )), где f B ( t ) — начальная сила сопротивления; d B ( t ) — начальная деформация; k ( t ) — жесткость выбранного линейного участка модели.
Прямая и обратная ветви гистерезиса характеристики жесткости в модели устройства накопления энергии представляются двумя наборами направленных линейных отрезков, которые выбираются, соответственно, при положительной или отрицательной скорости деформации. Изменение силы сопротивления прямой ветви описывается массивом значений f F , i , обратной — массивом f B,i . Значения соответствующих им деформаций задаются массивами d F,i и d B,i , каждому отрезку ветвей соответствуют коэффициенты жесткости k F,i и k B,i , где i = i FP = 1 при нахождении штока в ПП; i = i RP — при его полностью втянутом положении.
Для вычисления силы сопротивления в зависимости от величины текущей деформации d ( t ) и ее скорости выбирается один из участков прямой или обратной ветви. При смене знака скорости деформаций осуществляется переход между прямой и обратной ветвями по временному, переходному двунаправленному линейному отрезку, допускающему скорости деформации обоих знаков. Он соответствует (в данной модели для упрощения) максимальной жесткости k S механического упора.
В переднем положении штока сила fFFP сопротивления его втягиванию положительна для того, чтобы все штанги вместе обеспечивали силу сопротивления кольца, необходимую для срабатывания защелок даже при полностью выдвинутых штоках. Поэтому при растяжении штанги сила сопротивления сначала изменяется от fF,1 = fFFP до нуля, затем проходится зона люфта (нулевое значение силы), а после этого отрицательная сила реакции штанги нарастает до максимальной по модулю величины — fFmRax, определяемой настройкой фрикциона УОМ. В данной модели при деформациях растяжения гистерезис не учитывается, так как он значительно меньше, чем гистерезис ПМ. Поэтому ветвь растяжения описывается двунаправленными отрезками, допускающими оба знака скорости деформации. Жесткость при растяжении принимается равной жесткости kS механического упора штанги.
Все состояния модели, соответствующие нахождению на той или иной ее ветви, нумеруются для обеспечения логики перехода между ними и воспроизведения гистерезиса. Прямой его ветви соответствует состояние 1, обратной — состояние 2, двунаправленному переходному отрезку между ветвями 1 и 2 — состояние 3. Люфту при растяжении соответствует состояние 0, двунаправленному отрезку растяжения из прямой ветви до люфта — состояние 4, двунаправленному отрезку растяжения от люфта до максимального значения силы, ограниченной фрикционом УОМ, — состояние 14. Механическому упору при сжатии штанги в ее втянутом положении соответствует состояние 5. Концы переходных отрезков, соответствующих состояниям 3, 4 и 14 модели, описываются следующими парами координат: (d3Beg(t), f3Beg(t)) и (d3End(t), f3End(t)); (d4Beg(t), 0) и (d4End(t), f4End(t)); (d1B4eg(t), –fFmRax) и (d1E4nd(t), 0). Отрезок [d1E4nd(t), d4End(t)] соответствует зоне люфта. Способы вычисления переменных координат концов переходных отрезков — абсцисс (деформаций) и ординат (сил) — аналогичны приведенным в работе [14].
Геометрическое представление кусочнолинейной модели гистерезиса осевой деформации штанги, позволяющей рассчитать силу сопротивления перемещению ее штока, приведено на рис. 2. Для наглядности прямая и обратная ветви, переходные отрезки имеют различные цвета, цифры в прямоугольниках обозначают состояния модели. Условия изменения состояний модели представлены в таблице. Их выполнение обеспечивается выбором соответствующей величины шага интегрирования.
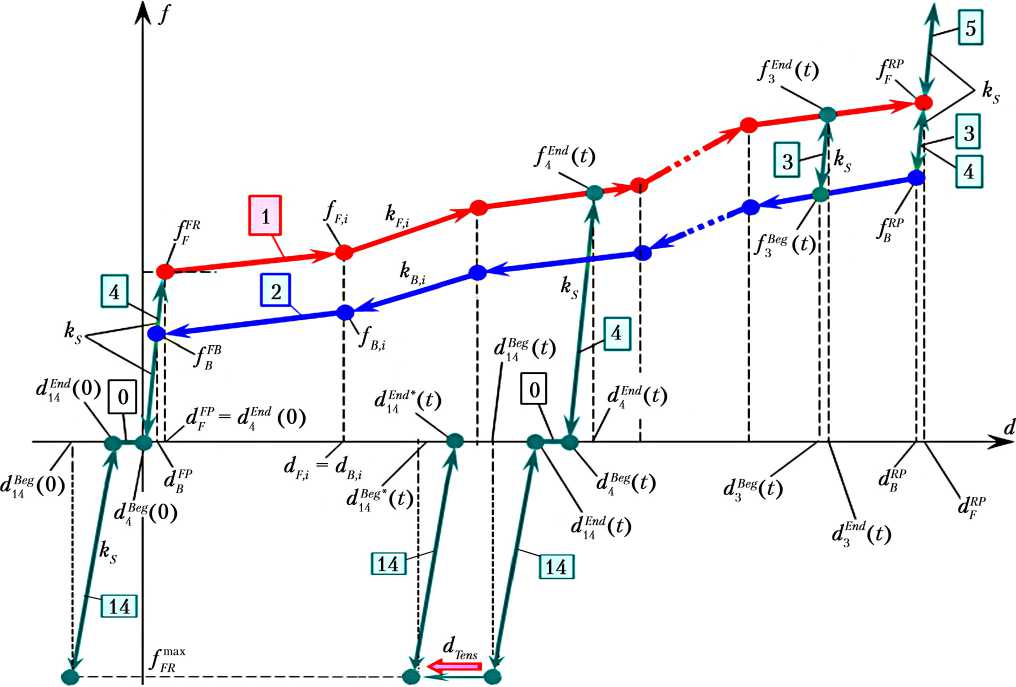
Рис. 2. Геометрическое представление модели гистерезиса при осевой деформации штанги для расчета сил устройства накопления энергии
Примечание. Математические величины пояснены в тексте, цифрами отмечены состояния математической модели в таблице.
Изменение состояния модели осевой деформации штанги
|
П р ед ш еству ю щ ее сост о я н и е |
Усл о ви я п ер ех о д а |
Н ов о е со стоя н и е |
В ы ч и сл ен и е к о о р д и н ат о тр езк ов ветвей |
|
0 |
d < d 1 E 4 nd |
14 |
Не требуется |
|
d > d Beg 4 |
4 |
Не требуется |
|
|
d 1 E 4 nd < d < d 4 Beg |
0 |
Не требуется |
|
|
Блокировка отдачи пружинного механизма выключена |
|||
|
1 |
d < 0 |
3 |
( d 3 Beg ( t ), f 3 Beg ( t )); ( d 3 End ( t ), f 3 End ( t )) |
|
d. > 0 |
1 |
Не требуется |
|
|
3 |
d > d 3 End |
1 |
Не требуется |
|
d < d 3 Beg |
2 |
Не требуется |
|
|
2 |
d. > 0 |
3 |
( d 3 Beg ( t ), f 3 Beg ( t )); ( d 3 End ( t ), f 3 End ( t )) |
|
d. < 0 |
2 |
Не требуется |
|
|
d. < 0, d < dBFP |
4 |
Не требуется |
|
|
Блокировка отдачи пружинного механизма включена |
|||
|
1 |
d > d 1 KP |
5 |
Не требуется |
|
d. < 0 |
4 |
d 4 Beg ( t ); ( d 4 End ( t ), f 4 End ( t )); ( d 1 B 4 eg ( t ), – f F m R ax ); ( d 1 E 4 nd ( t ), 0) |
|
|
5 |
d < d 1 KP |
4 |
|
|
d ≥ d 1 KP |
5 |
Не требуется |
|
|
4 |
d 1 E 4 nd < d < d 4 Beg |
0 |
Не требуется |
|
d > d 4 End < d 1 KP |
1 |
Не требуется |
|
|
d > d 4 End = d 1 KP |
5 |
Не требуется |
|
|
d 4 Beg ≤ d < d 4 End |
4 |
Не требуется |
|
|
d < d 1 E 4 nd = d 4 Beg |
14 |
Не требуется |
|
|
14 |
d 1 E 4 nd < d < d 4 Beg |
0 |
Не требуется |
|
d < d 1 B 4 eg |
14 |
d Tens = d – d 1 B 4 eg < 0; d Beg = d Beg + d ; 14 14 Tens d End = d End + d ; 14 14 Tens d Beg = d Beg + d ; d En d = d En d + d ; 4 4 Tens 14 14 Tens d F,i = d F,i + d Tens ; d B,i = d B,i + d Tens |
|
|
3 |
— |
4 |
d 4 Beg ( t ); ( d 4 End ( t ), f 4 End ( t ) ); ( d 1 B 4 eg ( t ), – f F m R ax ); ( d 1 E 4 nd ( t ), 0). |
|
2 |
— |
4 |
|
Пр и м еч а н и е. М атематические величины пояснены в тексте.
Модели устройств накопления энергии отдельных штанг до начала интегрирования УД стыковки последовательным уменьшением ходов штоков (увеличением деформации сжатия ПМ) переводятся из состояния 0 в состояние 1 , соответствующее их ИП, которое сохраняется вследствие включенной блокировки отдачи ПМ. При этом ход t i каждого штока находится в диапазоне ( t m IP in , t m IP ax ), величина которого определяется зоной нечувствительности контактного устройства.
В процессе моделирования процесса стыковки при потере сигнала исходного положения в –любой из штанг, т. е. при t i < t m IP in , i ∈ 1, 6, блокировки отдачи пружинного механизма всех штанг отключаются до сцепки. Поэтому в зависимости от контактных сил, действующих на стыковочное кольцо, модели отдельных устройств могут оставаться в состоянии 1 , либо через состояние 3 переходить в состояние 2 .
При достижении сцепки вновь включаются блокировки отдачи всех ПМ, и после этого модели устройств могут находиться только в состояниях 1 , 5 , соответствующих сжатию без отдачи, или в состояниях 4 , 0 и 14 , соответствующих растяжению. При срабатывании (проскальзывании) фрикциона, ограничивающего силу растяжения, т. е. при наличии его отрицательного хода d Tens < 0, происходит смещение начала координат по оси деформаций, и абсциссы всех отрезков модели изменяются на эту величину. Такая модель устройства накопления энергии обеспечивает «фильтрацию» вычислительного шума и корректное воспроизведение гистерезиса при численном интегрировании УД СтМ.
Расчет сил, создаваемых устройством стягивания
В приводе устройства стягивания два дублирующих электродвигателя связаны с выходным валом через дифференциал, который имеет две степени свободы и описывается УД с постоянными коэффициентами [15]. В модели привода к двум основным колесам дифференциала приведены моменты инерции роторов, электромагнитные моменты и моменты противо-ЭДС двух электродвигателей. К водилу приведен суммарный момент m D L r o i a v d e нагрузки на выходном валу, определяемый моментами нагрузки на силовые редукторы вследствие натяжения тросов. Действие стопорных муфт приближенно учитывается присвоением ω i = 0 при sign(ω i )sign( U i ) < 0, где i — номер колеса дифференциала; ω i — его скорость вращения; U i — напряжение питания электродвигателя. Скорость вращения и угол поворота выходного вала привода пересчитываются в скорости и углы поворота выходных валов силовых редукторов (углы — с учетом деформации гибких валов).
Далее рассматривается способ вычисления сил натяжения тросов под действием ПМ устройств накопления энергии и силовых редукторов. Предполагается, что углы пов–орота кулачков барабанов ϕ CamR,i ≥ 0, i = 1, 3. Равенство имеет место только при полностью втянутых тросах и СтМ. Положительная скорость вращения ω CamR,i кулачков барабанов соответствует удлинению тросов, отрицательная — их втягиванию.
Во время выдвижения СтМ из полностью втянутого положения перед стыковкой привод, редукторы и барабаны вращаются в положительном направлении, освобождая тросы, которые вытягиваются кольцом под действием ПМ устройств накопления энергии в штангах. При достижении ИП отдача ПМ штанг блокируется, длины тросов между барабанами и кольцом после этого не изменяются, но привод продолжает работать, увеличивая угловое расстояние между кулачками силовых редукторов и барабанов. При этом кулачки барабанов сохраняют свое положение под действием слабых пружин, связывающих выходные валы редукторов и валы соответствующих барабанов. Эти пружины создают малые силы натяжения тросов: f S T p e r n i s ng,i > 0, прилагаемые к барабанам, и – f S T p e r n i s ng,i , прилагаемые к кольцу. Знаки этих сил определяются направлением оси X B системы координат основания СтМ. Так как | f S T p e r n i s ng,i | значительно меньше сил ПМ штанг, то они практически не оказывают существенного влияния на выдвижение кольца из ИП вперед для улучшения сцепки.
Для увеличения запаса длины троса используется дополнительный, промежуточный кулачок барабана. Поэтому положительные углы поворота кулачков силовых редукторов при ослаблении тросов после выхода СтМ в ИП изменяются в пределах ϕ + 2Δϕ ≤ ϕ ≤ ϕmax , CamR,i Cam CamG,i CamG где ϕCmaamxG = 2π – 4ΔϕCam — максимальный угол поворота, при достижении которого привод выключается; ΔϕCam — одинаковый угловой размер всех кулачков.
Втягивание троса приводом начинается, когда кулачок редуктора, вращаясь в отрицательном направлении, упирается в промежуточный кулачок, а через него — в кулачок барабана, т. е. при
ϕ CamG,i < ϕ CamR,i + 2Δϕ Cam . (1)
Это же условие должно выполняться при выдвижении штоков штанг в ИП под действием своих ПМ. Штоки выдвигают стыковочное кольцо, натягивая тросы, а привод через редукторы и барабаны постепенно освобождает их длину.
После завершения накопления энергии сближения КА вследствие включенной блокировки отдачи ПМ штанг стыковочное кольцо остается в положении, для которого в общем случае характерны линейные и угловые отклонения от ИП (рис. 3). Длины свободных частей тросов равны расстояниям dRR,i между точками их схода с барабанов и крепления на кольце. Эти расстояния однозначно определяют положительные углы поворота кулачков барабанов ϕ = d – L RP /R , где L RP — длина
CamR,i RR,i Cab l Roll, Cable свободной части троса при полностью втянутом СтМ; RRoll — радиус барабана.
Положительные углы поворота кулачков силовых редукторов равны ϕCamG,i = (ϕDrive – ΔϕFS,i)/iGear, где ΔϕFS,i — угловые деформации гибких валов; iGear — коэффициент редукции силового редуктора; ϕDrive — угол поворота выходного вала привода. При втягивании тросов и СтМ скорости вращения привода и редукторов отрицательные, т. е. ωDrive < 0, ωGeari < 0. Поэтому первым начинает вращаться барабан, кулачок которого наиболее близок к кулачку редуктора, т. е. имеет максимальное значение угла ϕCamRi (для него условие (1) начинает выполняться первым по мере уменьшения положительного угла ϕCamG,i). Это соответствует максимальной величине dRR,i, т. е. первым начинает втягиваться трос с наиболее длинной свободной частью. На рис. 3 это имеет место для троса справа. Для более короткого троса (на рис. 3, слева) угол ϕCamRi имеет меньшее значение,
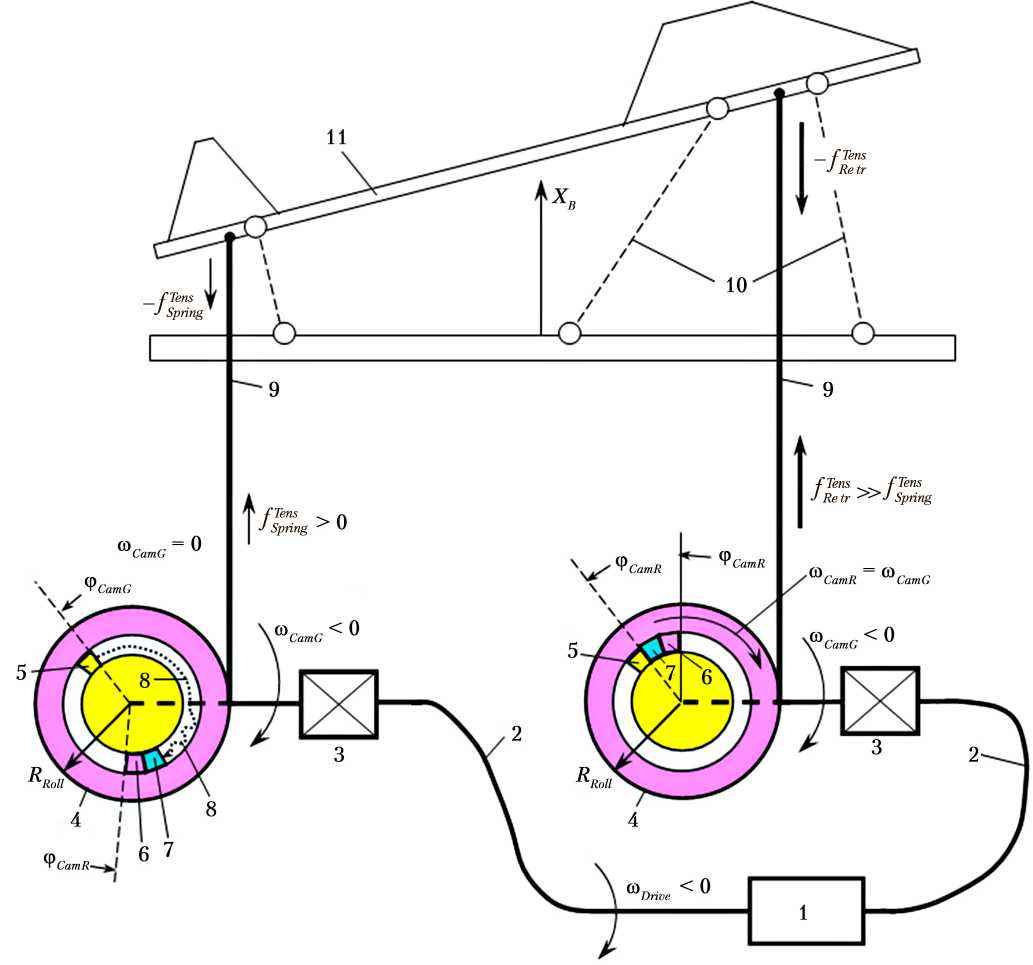
Рис. 3. Относительное положение кулачков барабанов и силовых редукторов ненатянутого (слева) и натянутого (справа) тросов при их втягивании: 1 — электропривод; 2 — гибкий вал; 3 — силовой редуктор; 4 — барабан намотки троса; 5 — кулачок силового редуктора; 6 — кулачок барабана; 7 — промежуточный кулачок для увеличения углового хода; 8 — пружина барабана; 9 — трос; 10 — штанги СтМ (условно); 11 — стыковочное кольцо
Примечание. Математические величины пояснены в тексте.
угловое расстояние между кулачками редуктора и барабана больше, и движение барабану не передается, его скорость вращения равна нулю. При продолжении втягивания (уменьшении угла ϕ CamG,i ) кулачок редуктора входит в контакт с кулачком барабана более короткого троса, начиная втягивать его. Это обеспечивает выравнивание СтМ.
Начиная с момента t Join,i начала совместного вращения кулачков редукторов и барабанов i –го троса, постепенно нарастают суммарные изменения расстояния между его точками схода с барабана и крепления на кольце
t
ΔdRΣR,i(t) = Σ (dRR,i(t) – d Rp rRe,i;(2)
t Join,i суммарное изменение длины части троса, намотанной на барабан,
∆lΣ (t) = R Σt (ϕ (t) – ϕprev )(3)
Cable Rollt CamG,i Ca m G ,i и отрицательная деформация
∆Def = ∆lΣ (t) – ΔdΣ (t) ≤ 0,(4)
Cable,i Cable,i RR,i где d prev, ϕ p re v — значения величин на пред-R R ,i , Ca m G , шествующем шаге интегрирования.
При выдвижении тросов, т. е. при выдвижении штоков штанг в ИП, ΔdRΣRi(t) > 0; ∆lCΣable,i(t) > 0, но |ΔdRΣR,i(t)| > |∆lCΣable,i(t)|,, поэтому по-прежнему ∆CDaebfle,i ≤ 0. Скорости изменения деформаций тросов равны v CDaebfle,i = vL,Cable,i (t) – vRR,i(t) =
= ω R – nT (v + αTω~ l ), (5) CamG,i Roll Cable,i R R R CableR,i , где nCablei и vR — единичный вектор свободной части натянутого троса и скорость центра стыковочного кольца в системе координат (СК) основания СтМ, соответственно; ωR, lCableR,i — угловая скорость кольца и вектор из его центра в точку крепления троса, выраженные в СК кольца; αR — матрица преобразования из СК основания в СК кольца СтМ.
При втягивании тросов силы их натяжения, прилагаемые к барабанам, равны f Tens = –kS ∆Def – cS vDef > 0 (6)
Re tr,i Cable Cable,i Cable Cable,i , где kCSable, cCSable — коэффициенты жесткости и демпфирования.
Моменты сил натяжения тросов на выходные валы силовых редукторов mTGeenasr,i = fRTeentrs,iRRoll суммируются на выходном валу привода mDLroiavde = ( Σ=1mRTeentsr,i)/iGear. Векторы силы и момента, действующие на стыковочное кольцо со стороны тросов, равны
Cable 3 Tens 3 f Tens
R i =1 ( Re tr,i ) i Σ =1 ( n Cable,i Gears,i );
m Cable = l R × ( α f Tens ), (7)
R i =1 Cable,i R Re tr,i , где lRCablei — векторы из центра кольца в точки крепления тросов.
Векторы силы и момента, действующие на основание СтМ, определяются аналогично. Угловые деформации гибких валов равны Δϕ = (m Tens /i )/k , где k — FS,i Re tr,i Gear FS,i, FS,i жесткость гибкого вала на кручение, определяемая его длиной.
В процессе стягивания СтА происходит постепенный набор относительной угловой скорости КА вследствие их инерции. В результате, для отдельных тросов скорости точек их крепления на кольце могут превышать скорости их втягивания, что приводит к их нулевой деформации и отводу кулачков барабанов от кулачков приводов под действием пружин, т. е. к нарушению условия (1). В этом случае времена t Join,i начала совместного вращения кулачков и суммы (2)–(4) обнуляются, силы натяжения тросов не вычисляются. При дальнейшем стягивании контакты кулачков редукторов и барабанов восстанавливаются, и вычисления по соотношениям (2)–(7) возобновляются.
Заключение
Разработанная математическая модель динамики нового периферийного стыковочного механизма учитывает все его основные особенности — кинематику, инерцию и формирование внутренних активных сил отдельными устройствами. Она входит в состав модели стыковки, предназначенной для анализа динамики этого процесса.
Список литературы Математическая модель динамики периферийного стыковочного механизма с накоплением кинетической энергии сближения космических аппаратов
- Яскевич А.В., Чернышев И.Е. Выбор параметров накопителя энергии для нового периферийного стыковочного механизма // Космическая техника и технологии. 2019. № 2(25). С. 55-66. DOI: 10.33950/spacetech-2308-7625-2019-2-55-66
- Рассказов Я.В. Устройство накопления энергии нового периферийного стыковочного механизма // Космическая техника и технологии. 2019. № 3(26). С. 39-47. DOI: 10.33950/spacetech-2308-7625-2019-3-39-47
- ТУ-22-178-02-90. Валы гибкие проволочные с броней. Режим доступа: http://www.uzgv.ru/Catalog.aspx (дата обращения 10.01.2019 г.).
- Яскевич А.В. Комбинированные уравнения движения для описания динамики стыковки космических аппаратов с помощью системы "штырь-конус" // Космические исследования. 2007. Т. 45. № 4. С. 325-336.
- Яскевич А.В. Контактные силы в уравнениях движения космических аппаратов при стыковке и причаливании // Космическая техника и технологии. 2018. № 2(21). С. 80-92.
- Яскевич А.В. Алгоритмы определения параметров контактов при моделировании стыковки и причаливания космических аппаратов // Космическая техника и технологии. 2018. № 3(22). С. 90-102.
- Gough V.E., Whitehall S.G. Universal tyre test machine // Proceedings of the FISITA Ninth International Technical Congress. May, 1962. P. 117-137.
- Stewart D. A platform with six degrees of freedom // Proceedings of the Institution of Mechanical Engineers. 1965. V. 180. Part 1. № 15. P. 371-386.
- Степаненко Ю.А. Алгоритм анализа динамики пространственных механизмов с разомкнутой кинематической цепью / В сб. ст. Механика машин. М.: Наука, 1974. Вып. 44. С. 77-88.
- Walker M.W., Orin D.E. Efficient dynamic computer simulation of robotic mechanisms // Trans. ASME, Journal of Dynamic Systems, Measurement and Control. 1982. V. 104. P. 205-211.
- Яскевич А.В. Уравнения динамики стыковочных механизмов. Ч. 1. Алгоритмы для механических систем со структурой дерева // Мехатроника, автоматизация, управление. 2018. Т. 19. № 1. С. 58-64.
- Wehage R.A., Haug J.E. Generalized coordinate partitioning for dimension reduction in analysis of dynamical systems // Journal of Mechanical Design. 1982. № 104. P. 247-255.
- Яскевич А.В. Уравнения динамики стыковочных механизмов. Часть 2. Алгоритмы для кинематических контуров // Мехатроника, автоматизация, управление. 2018. Т. 19. № 2. С. 139-144.
- Яскевич А.В. Математические модели гистерезиса, описывающие деформации механизмов для стыковки космических аппаратов // Электронный журнал "Труды МАИ". 2015. № 83. 23 с. Режим доступа: https://mai.ru/upload/ iblock/98d/yaskevich_rus.pdf (дата обращения 20.06.2019 г.).
- Яскевич А.В. Математическая модель периферийного стыковочного механизма. Ч. 1. Уравнения движения дифференциальных механизмов // Мехатроника, автоматизация, управление. 2012. № 7. С. 63-70.


