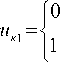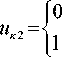Математическая модель дискретно-фазовых преобразователей перемещений вращающихся узлов энергоагрегатов

Обеспечение высокой надёжности вращающихся узлов (ВУ) изделий машиностроения, например, энергетических установок (ЭУ) на базе турбоагрегатов, увеличение их эксплуатационного ресурса и снижение эксплуатационных расходов основано на использовании информации о фактическом состоянии их нагруженных вращающихся конструкционных элементов. По этой причине разработка эффективных автоматизированных средств диагностики и контроля текущего состояния элементов вращающихся силовых узлов ЭУ является актуальной научно-технической задачей. При этом основными диагностическими параметрами являются статические и динамические угловые и линейные перемещения (УЛП) этих элементов, вызванные статической закруткой, изгибом и крутильными колебаниями элементов ВУ ЭУ.

В качестве примера на рис. 1 а схематически представлена ступень лопаточной ЭУ. Здесь элементы конструкции ротора (диск колеса и вал) при их вращении совершают угловые статические (в виде закрутки) и динамические (в виде колебаний) перемещения относительно оси вала ОО, а также линейные перемещения в направлении осей Х и Y. Под действием рабочего тела (газовоздушной смеси или жидкости) на лопатки ЭУ их торцы подвергаются осевым перемещениям (ОП) вдоль оси Х и радиальным перемещениям (в пределах рабочего зазора - РЗ) вдоль оси Y (рис. 1 б ). Торец лопатки в результате закрутки её пера может совершать статические и динамические угловые перемещения (УП) в пределах некоторого угла ф (рис. 1 в ) в плоскости ХОZ. Кроме этого, в результате изгибных перемещений (ИП) пера лопатки её торец перемещается вдоль оси Z (рис. 1 г ). При этом (см. боковую проекцию на рис. 1 г ) нормаль торца лопатки отклоняется от исходного состояния на угол а . В корпусе ЭУ над траекторией движения торцов лопаток установлен преобразователь перемещений (ПП), чувствительный элемент (ЧЭ) которого изображён на рис. 1 в .

На практике как для оперативного, так и длительного контроля УЛП элементов ВУ ЭУ чаще всего применяется бесконтактный дискретно-фазовый метод (ДФМ) [1,2].

Рис. 1. Элементы ротора лопаточной энергетической установки (а) и развёртка лопаточного венца с линейными (б) и угловыми (в, г) перемещениями лопаток

Сущность ДФМ основана на преобразовании дискретных значений (фаз) перемещений контролируемых элементов (торцов лопаток, рис. 1) в пределах каждого оборота ротора Tp ВУ в пропорциональные временные интервалы Ati между опорным (корневой датчик) и информационным (периферийный датчик) импульсами. Значения длительностей Ati накапливаются на интервале T >> nTp, n >> 1, n -число оборотов ротора ВУ. В результате из массива на- копленных данных выделяются A t max~ymax, A t mh,~ymin и A tcp ~Уср , гДе У max, У min, Уср - максимальное, минимальное и среднее значения контролируемого перемещения за время накопления (усреднения) информации.

Однако внедрение известного метода дискретнофазовых измерений сдерживается из-за необходимости выполнения глубокого препарирования энергоагрегата для установки датчиков в его внутреннем тракте. Установка внутренних датчиков требует монтажа дополнительных крепёжных, токосъёмных и других конструктивных элементов, что снижает надёжность как устройства контроля, так и ЭУ в целом. Кроме того, рассмотренный ДФМ имеет существенный недостаток, связанный с резким уменьшением чувствительности при измерении УЛП, обусловленных высшими формами колебаний элементов ВУ.

Анализ современного состояния научно-технической проблемы бесконтактного контроля УЛП динамически нагруженных элементов ВУ изделий машиностроения показал, что непрерывно возрастающие требования к точности и достоверности контроля перемещений элементов ВУ вызывают необходимость создания нового поколения устройств, которые в силу специфики построения и методики использования целесообразно выделить в самостоятельный класс средств измерений – дискретно-фазовые преобразователи перемещений (ДФПП) [3].

Особенность преобразователей данного класса заключается в том, что значения дискретных фаз перемещений формируются с помощью расположенного в технологическом отверстии корпуса энергетической установки (ЭУ) одноканального или двухканального первичного преобразователя, в котором конструктивно и функционально интегрированы объект контроля, источник и приёмник зондирующего излучения (ЗИ) оптического или радиоволнового диапазона, а также электронные узлы первичной обработки сигналов. Использование оптического и радиоволнового диапазонов для формирования ЗИ объективно несёт в себе бóльшие возможности информативного взаимодействия с контролируемым объектом по сравнению с традиционной реализацией ДФМ [4,5]. Однако детальные исследования комплекса эксплуатационных характеристик ДФПП невозможны без решения основной проблемы теории преобразователей рассматриваемого класса - разработки их обобщённой математической модели (ОММ).

Угловое перемещение контролируемого элемента a (рис. 1 г ) является наиболее общим случаем при рассмотрении УЛП ВУ ЭУ, поэтому на его примере рассмотрим построение ОММ.

Методика формирования обобщённой математической модели

Под обобщённой математической моделью ДФПП будем понимать уравнение, связывающее между собой значения выходного кода преобразователя с измеряемой величиной через конструктивные и схемотехнические параметры и их отклонения от номинальных значений. Для получения ОММ необходимо получить математические модели процессов формирования и преобразования сигналов в их аналоговых, аналого-цифровых и цифровых функциональных элементах. К таким процессам относятся:

• • формирование опорного и информационного сигналов;

• • преобразование информативного временного интервала в код, а именно:

  – компарирование сигналов и формирование прямоугольного импульса, длительность которого пропорциональна измеряемой величине;

  – генерация прямоугольных тактовых импульсов;

  – формирование «пачки» прямоугольных импульсов, количество которых пропорционально измеряемому временному интервалу;

  – определение значений разрядных цифр.

Формирование математических моделей опорного и информационного сигналов

В случае использования двухканального ПП информативные временные интервалы определяют угловые положения a контролируемых элементов ВУ. В основу таких ДФПП положен физический принцип зависимости отражающих свойств поверхностей материалов от качества их обработки и частоты электромагнитного излучения. Сущность заключается в том, что пространственное положение максимума индикатрисы потока, отражённого от поверхности контролируемого элемента зеркально ( X >  8 h , где X - длина волны ЗИ, а h - высота микронеровностей ПКО – поверхности контролируемого объекта), определяется его угловым положением a . Индикатриса диффузно отражённого потока ( X <  h ) имеет практически круговой вид, и поэтому положение её максимума в малой степени зависит от угловой ориентации отражающего участка. Таким образом, если зафиксировать во времени положения максимумов индикатрис обоих потоков, отражённых от поверхности контролируемого элемента, то по временному интервалу между ними можно судить о величине его углового перемещения a .

Отражённые потоки ЗИ с помощью первичных электронных устройств преобразуются в импульсные электрические сигналы и_ин ф ( t ) и u_on ( t ) , временные положения максимальных значений которых u ™ ( t ) и u ™ ( t ) определяют информационные временные интервалы:

^A t = t = arg u max ^- arg u™ ~ ^a .                  ⁽¹⁾

Для описания процессов получения и инф ( t ) и и_оп ( t ) введём в рассмотрение совокупности номинальных ( c 01 , c 0₂ ,... c 0 j ,..., c 0 _K m ) и фактических

( c r 1 , c r 2 , ... c r

rj ^,..

., crK ) значений конструктивных, схемотехнических и энергетических параметров, соответствующих идеальному и реальному ДФПП. В этих выражениях r ={ p, f, s, g, X, h} - обобщённый индекс, определяющий вид используемых частных математических моделей, а именно: p – индекс, обозначающий параметры мощности P ЗИ с длиной волны X, f - индекс нормированной функции F пространственной модуляции ЗИ, s – индекс крутизны S энергетического преобразования потока ЗИ в ток приёмного устройства, g – индекс, обо- значающий схемотехнические и технологические параметры электронных устройств, h – индекс, характеризующий высоту микронеровностей ПКО.

Разности Acrj = c0j - crj образуют совокупность (Acr 1, Acr2,... Acrj,..., Acrk) отклонений параметров от номинальных значений, являющихся следствием влияния инструментальных погрешностей и внешних факторов. С учётом введённых обозначений математическая модель формирования информационного и опорного аналоговых электрических сигналов от воз действия ЗИ j -той элементарной площадки излучателя без учёта погрешностей энергоинформационных преобразований получена в виде:

^иинф, ( ^а , ^Q t) = ^Pj⁽ c P , A с p ^cX , A c x ) X

X F j⁽ a , ^Q t ,c^f , ^A c f _ c h , ^A c h ) x>8 h ^X                (2)

x S j ( c f , A c s ,c X , A c x )Z„ ,

^nj (a, Q t) = Pj( cP , A cp cX , A cx ) X xFj(a,Qt,cf,Acf,ch,Ach)|x

xSj(cf, Acs,cX,Acx )Z„.

Суммирование воздействий потоков ЗИ всех элементарных излучателей после отражения от ПКО по всем элементарным площадкам приёмника-преобразователя позволяет на основании (2 и 3) получить информационный и опорный электрические сигналы в виде:

^иинф^(a, ^Qt) =

^Uon^(a, ^Qt) =

N

L Pj⁽c⁰ , ^AcP , cX , ^Acx )Fj^(a, ^Qt, c■ , ^Acf , c^{0, A}ch ) X>8h j=1

K

L Sk⁽c^{0, A}cs, c^f,^AcX )

k=1

Zн

X

N K                          N K

LL jk^(AcP,^Acf,^Acs)^{+1 +}EL^jk^(AcP,^Acf,^Acs), j=1 k=1                                    J    j=1 k=1

N

L Pj⁽cP, ^AcP , cX, ^Acx )Fj^(a,^Qt, c^f , ^Acf , c^{0, A}ch ) |X<h j=1

N K x LL^jk(AcP,Acf,Acs)+1

j=1 k=1

K

L ^Sk⁽cs ’ ^Acs ’ cX ’ ^AcX ) | ^Zh^X k=1

NK

⁺LL^»^(AcP,^Acf,^Acs), j=1 k =1

где a - угловое положение ПКО; ZH - сопротивление нагрузки; t - текущее время, Q - частота вращения контролируемого элемента, ^jk - мультипли кативная и уjk - аддитивная составляющие погрешности энергоинформационного взаимодействия ЗИ с ПКО; N – количество элементарных излучателей, формирующих ЗИ, K – количество элементарных приёмных элементов.

Формирование обобщённой математической модели преобразователя временного интервала в код

При построении обобщённой математической модели время-импульсного цифрового преобразователя N(a) необходимо учесть наиболее существен- ные процессы, которые влияют на точность преобразования. К ним относятся процессы генерации счётных импульсов, компарирования сигналов, ло- гической обработки и счёта импульсов.

Выходной сигнал генератора тактовых импуль- сов (ГТИ) в соответствии с [6, 7] представим в виде:

uг

1 при    iTr < t < (2i +1) -^, f при (2i +1) -г < t < (i + 1)-г,

(6),

где i = f, 1, 2^N - номер периода колебаний ГТИ.

Временные моменты начала инкрементирования счётчика и его остановки определяются в результате сравнения информационного и опорного сигналов, определяемых выражениями (4), (5), с пороговыми напряжениями компараторов u_п1и u_п2:

при ^иинф⁽t) < un 1, при ^иинф⁽t) > un 1,

при uon⁽t) < un2, при uon⁽t) > un2-

Импульс напряжения, длительность которого пропорциональна входной измеряемой величине, определится как: u_т(a) = ик₁л ик₂. Тогда сигнал («пачка» импульсов) на входе счётчика: исч (a) = ик₁л ик₂л иг также является функцией выражений (4) и (5). Иными словами, и_сч = f (a, c^f, Ac_r).

Модель i -ой разрядной цифры двоичного счётчика [7]: a”⁺¹= Tn a,” + Tn a,” , где Tⁿ - фронт или потенциальный уровень напряжения на счётном входе Т-триггера, изменяющие состояние i -разряда счётчика. Учитывая, что Tⁿ = и^ч, выражения для значений разрядных цифр асинхронного двоичного счётчика определятся в виде:

n+1        n      n , nn dlx — U " CL\ " CL\ ,

0         cч    0 cч0 n +1        n +1     n       n +1

^1   = a о   ■ ai + a 0   ■ n +1        n +1     n       n +1

а 2   = ai   ■ a 2 + ai   ■ n +i        n +i      n          n +i m-1     m-2   m-1     m-2

.

Значения разрядных цифр a_i также зависят от (а, с0, Асr), и их можно представить в виде логических функций действительных аргументов:

й = {0(а,с0, Асr ),1(а,с0, Асr)}.

В теории кодирования полученную кодовую комбинацию обозначают кодовым вектором a с размерностью m : a = (a0,a₁,...am_-1), представляемого в виде многомерного куба. Сложность интерпретации полученного результата не позволяет построить наглядные методы оценки основных метрологических эксплуатационных характеристик ДФПП и исследовать его технические возможности. Поэтому предлагается математическую модель ДФПП дополнить уравнением преобразования идеального ЦАП, включенного на выход ДФПП. В этом случае выходной код реального ДФПП, с учётом полученных соотношений для отдельных разрядов, представляется в виде обобщённого уравнения преобразования:

Nn⁺¹(а,с 0, Ас r) = u"_M (а,с0, Ас r) ■ On +

---------------- m -1                             (10)

+u"_M (а,с 0, Ас r) ■ an -У an⁺¹ (а,с 0, Ас r) ■ 2i.

i=1

Уравнение (10) определяет весь комплекс метрологических характеристик реального ДФПП.

Приравнивая Ас_r = 0 , т.е. исключая влияние инструментальных погрешностей, можно получить обобщённое уравнение преобразования идеального ДФПП:

Nn⁺¹(а, с 0) = и"_И (а, с 0) ■ an +

----------- m-1                                  (11)

+и"_И (а, с 0) ■ an +£ ai⁺¹(а,с0) ■ 2i. i=1

Числовой массив значений инструментальной погрешности определения углового перемещения а может быть найден по разности:

АN(а) = Nn+1 (а,с0, Асr)- Nn+1 (а,с0), которая представляет собой последовательность прямоугольных импульсов, длительность которых определяет значения погрешности в k -ой точке смены выходного кода, а полярность определяет её знак.

Заключение

В результате проведённых исследований впервые разработана методика получения обобщённой математической модели ДФПП, в виде уравнения идеального цифро-аналогового преобразования вы- ходного кода ДФПП процессы изменения разрядных цифр которого заданы в виде логических функций от входного параметра а, множества конструктивных и внешних факторов, а также их отклонений от номинальных значений.

Полученная обобщённая математическая модель позволяет получать оценки метрологических характеристик ДФПП, включающих в себя:

– законы распределения суммарной погрешности;

– влияние на суммарную погрешность отдельных её составляющих;

– достоверность преобразований и др.

Программное моделирование Nu (а) и N_p (а) позволяет в соответствии с методикой, изложенной в [6,7], получать результаты, отображающие функции влияния отклонений отдельных параметров на результирующую погрешность преобразования.