Математическая модель длительных режимов передачи постоянного тока на базе преобразователя напряжения

Современные передачи постоянного тока (ППТ) все чаще выполняют на базе преобразователей напряжения (ПН). ПН работает во всех четырех квадрантах мощности и позволяет независимо регулировать активную и реактивную мощность и переменное напряжение, может работать на слабую сеть, в пределе на автономную нагруз-ку[1], а также имеет высокое быстродействие в динамических режимах и при реверсе переда-чи[2].Для анализа длительных и аварийных режимов передачи на базе ПН (ППТ-ПН), (см. рисунок)

необходима ее математическая модель, которая бы учитывала реальные взаимосвязи передачи с примыкающими энергосистемами. Использовать модели, созданные для передач постоянного тока с фазовым регулированием, не представляется возможным в силу другого принципа работы преобразователей. Модели, позволяющие проанализировать взаимодействия ПН с энергосистемой [3], не обладают универсальностью, достаточной для рассмотрения ППТ-ПН, связанных с энергосистемами, параметры которых могут меняться с изме-

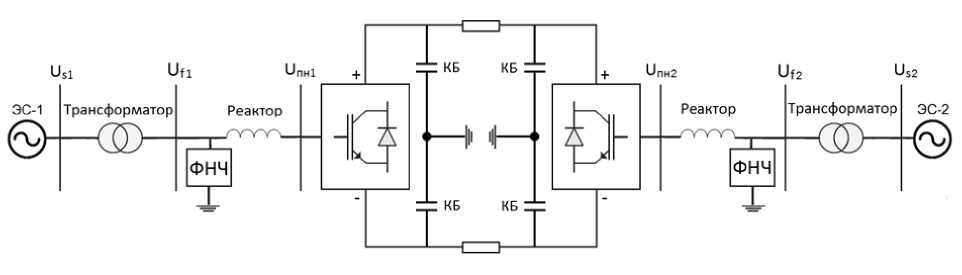
Схема ППТ–ПН

Гольдштейн М.Е., Корбуков Н.В.

нением состава генерирующих мощностей или нагрузок.

При разработке модели приняты следующие допущения: модель описывает только длительные режимы, специфика работы регуляторов не рассматривается, энергосистемы, трансформаторы и реакторы обладают только индуктивными сопротивлениями, напряжения сети симметричны и представлены только первой гармоникой, выпрямленное напряжение U d не имеет пульсаций и, наконец, преобразователи работают без потерь.

Сложив индуктивности системы, трансформатора и реактора, получим суммарное сопротивление между шинами системы с напряжением U s и шинами ПН с напряжением U пн :

x2 = xs + xt + xr .(1)

Межсистемный поток активной мощности:

P = Us • Uпн , sin 5.(2)

x 2

На постоянном токе активную мощность можно найти как:

Pd = Id • Ud .(3)

Так как потерями в ПН пренебрегаем, то из выражений (2) и (3) следует:

Id =     ' ' • sin 5-t^.(4)

x 2

x_{s 1} = 13,23 Ом, второй ЭС-2 соответственно: 110 кВ, S _кз2 = 500 МВА, x_{s 2} = 26,46 Ом . Преобразовательные трансформаторы 110/80 кВ мощностью S_mp = 120 МВА представлены сопротивлениями x t = 16,84 Ом, сопротивление реакторов x r = 9,24Ом сопротивление линии постоянного тока г _л = 1,8 Ом . Расчет проведем в относительных единицах для базисной мощности S _б = 100 МВА и средней ступени напряжения на высокой стороне трансформатора U _{ср ст} = 115 кВ.

Для стороны постоянного тока:

f u d - u d = i d R л ,

[ u d I d = P d /2,               (7)

где U_d ^в и U_d ^и – напряжения одного полюса.

Приняв U_d ^и = 80 кВ, P_d = 100 МВт, получаем:

U_d ^в= 81,11 кВ.                (8)

Для выпрямительной подстанции из (1):

** **

x ₂ = x *i + x t + x r = 0,10 + 0,167 + 0,144 = 0,411 о.е. (9)

Из выражений (5) и (2) при k m = 0,86 находим соответственно U пн1 = 77,01 кВ и угол δ:

5 = arcsin

**

P x 2 I I U s U п н J

Связь постоянного напряжения U_d с переменным для трехуровневого одномостового преобразователя [4]:

arcsin

Г 1 - 0,411 I 1 1 - 77,01/80 ^J

= 25,28 ° .

U пн

, 2n/3

¹ U ² dt ²

* { d    Л U d

km

km

,

где k_m – коэффициент широтно-импульсной модуляции.

Из уравнений (4) и (5) следует

2 U

Id =”R-, ----sin ⁵ .           ⁽⁶⁾

V³ • k m x 2

Измеренный по осциллограммам Matlab фазовый сдвиг сетевого напряжения и напряжения ПН совпал с расчетным.

Таким образом, разработанная математическая модель длительных режимов ППТ-ПН адекватна. В дальнейшем при развитии модели предстоит на основе исследований различных длительных и динамических режимов ППТ, в т. ч. асинхронной связи энергосистем расширить функциональные возможности модели как силовой части ППТ, так и ее регуляторов.

Выражения (5) и (6) связывают токи и напряжения на сторонах переменного и постоянного тока преобразователей. Таким образом, выражения (1)–(6) описывают нормальные длительные режимы ППТ-ПН при нормируемых коэффициентах модуляции ПН.

Адекватность математической модели в длительных режимах проверена в среде MatlabSimulink для биполярной ППТ мощностью 100 МВт напряжением ± 80 кВ. Параметры первой энергосистемы ЭС-1: 110 кВ, S _кз1 = 1000 МВА,