Математическая модель для анализа электромагнитных процессов в многозонном полупроводниковом преобразователе

В настоящее время в работах, посвященных разработкам устройств плавного пуска асинхронных и синхронных двигателей, особенно высоковольтных, актуальна проблема повышения их энергоэффективности [1–6]. Широко применяемые тиристорные регуляторы переменного напряжения (РПН), выполняющие роль устройств плавного пуска двигателей переменного напряжения, снижают пусковой ток (ПТ) двигателей, но существенно искажают его форму, что увеличивает потери активной мощности [7–9]. По данным ряда исследований, при медленном пуске последнее приводит даже к выходу двигателей из строя вследствие тепловых перегрузок [10, 11].

В настоящее время большинство выпускаемых промышленностью тиристорных регуляторов переменного напряжения сформированы по схеме со встречно-параллельным включением тиристоров [12, 13]. При разном уровне входного напряжения (0,4–10 кВ) тиристорная группа содержит от 1 до 5 последовательно включенных тиристоров. Такой вариант регулятора напряжения пред-

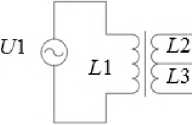
Рис. 1. Схема многозонного тиристорного регулятора с встречно-параллельными группами тиристоров

ставляет схему с зонным регулированием амплитуды выходного напряжения и фазовым регулированием момента включения тиристоров. Это способствует повышению качества ПТ, а также снижает величину броска пускового тока по сравнению с однозонным регулятором переменного напряжения [14]. На рис. 1 показана известная схема многозонного тиристорного регулятора с встречно-параллельными группами тиристоров. Недостатками такой схемы являются высокие относительные значения напряжений на тиристорах и наличие трансформатора.

В последнее время уделяется большое внимание развитию многозонных топологий регуляторов переменного напряжения, позволяющих улучшить качество пускового тока и снизить напряжение на полупроводниковых приборах [15]. Схемы многозонных тиристорного и транзисторного регуляторов напряжения приведены на рис. 2 и 3, соответственно. Как видно из представленных рисунков, этим схемам присуще наличие конденсаторных делителей напряжения в виде цепочек последовательно соединенных конденсаторов С 1, С 2 и т. д.

кп

—Н^-

VT2

VT4 Z1

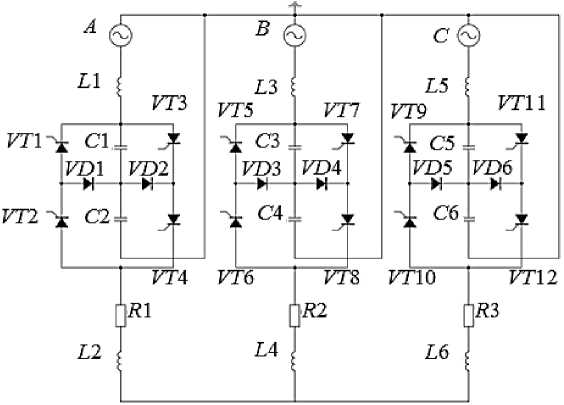
Рис. 2. Многозонный тиристорный регулятор напряжения

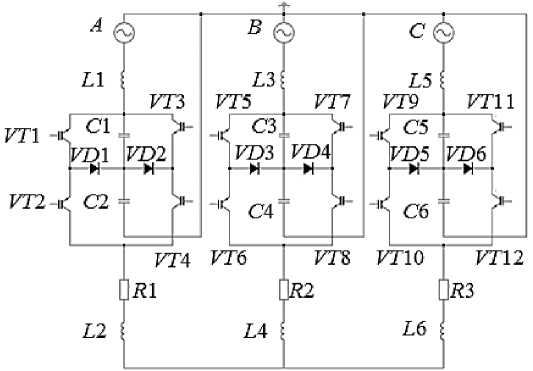
Рис. 3. Схема многозонного транзисторного регулятора напряжения

Конденсаторный делитель обеспечивает получение половинного напряжения сети без использования трансформатора, что дает два уровня входного напряжения регулятора, а значит, и две зоны регулирования выходного напряжения регулятора. Тиристоры с дополнительными фиксирующими диодами включены последовательными цепочками, включенными встречно-параллельно, что позволяет получить на всех полупроводниковых приборах половинную величину напряжения сети, что обусловливает снижение стоимости тиристоров по сравнению с трансформаторной схемой регулятора (см. рис. 1). Стоит отметить, что в данной схеме ток протекает в верхней зоне регулирования через два последовательных тиристора, а не один, как в схеме на рис. 1. Наличие цепочки из нескольких последовательно включенных тиристоров, обусловленных количеством n -зонных конденсаторных делителей напряжения [16], позволит снизить общие потери в тиристорах.

Для получения различных характеристик многозонных полупроводниковых преобразовате- лей в установившихся режимах требуется специализированное программное обеспечение (ПО), которому необходимо наличие высокопроизводительных аппаратно-вычислительных комплексов. Кроме того, для случаев множественных итерационных расчетов, необходимых для построения характеристик, понадобится большое количество расчетного времени. В этой связи становится актуальным использование математических моделей, позволяющих рассчитать электромагнитные процессы с меньшими затратами по временным и аппаратным ресурсам, в разработке которых стоит острая необходимость. Реализация таких моделей может быть осуществлена на базе спектрального метода с применением переключающих функций [17, 18].

Одной из ключевых характеристик многозонного полупроводникового регулятора напряжения является коэффициент гармоник тока, который позволяет оценить качество пускового тока двигателя. Также стоит отметить, что в некоторых случаях требуются более точные оценочные показатели, в роли которых выступает интегральный коэффициент гармоник высокого порядка. Для нахождения вышеописанного коэффициента гармоник требуется решение дифференциальных уравнений высокого порядка. Таким образом, использование математических моделей, реализованных с применением спектрального метода на базе переключающих функций [19], позволит избежать решения дифференциальных уравнений для нахождения параметров РПН в установившемся режиме. Для реализации таких моделей может быть использован легкодоступный математический пакет – Mathcad.

В связи с этим в статье предложена математическая модель, позволяющая проводить анализ электромагнитных процессов с возможностью расчета средних, действующих значений, коэффициентов гармоник токов и напряжений в элементах схемы многозонного тиристорного регулятора напряжения, а также получать их спектральный состав.

Математическая модельдвухзонного РПН

Для упрощения реализации математической модели пренебрежем потерями в полупроводниковых приборах и реактивных элементах схемы.

Процедуру получения математической модели для исследуемого типа регулятора напряжений разделим на ряд этапов. На первом этапе определяются переключающие функции в соответствии с законами коммутации полупроводниковых приборов. Это могут быть функции, описывающие дли-

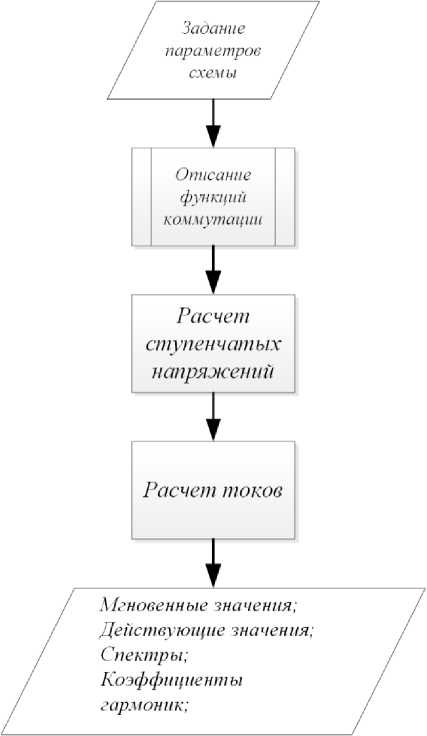
Рис. 4. Блок-схема реализации математической модели

тельности коммутации тиристоров, соответствующие их законам управления. Эти функции будут использованы для описания выходных напряжений устройств. На втором этапе выполняют математическое описание выходных фазных и линейных напряжений регулятора. На третьем этапе осуществляется математическое описание фазных токов данного регулятора напряжения, определение их мгновенных, средних и действующих значений и их спектральных составов.

Всю процедуру реализации математической модели рационально представить в виде блок-схемы (рис. 4). Каждый блок характеризуется ма- тематическим описанием электромагнитных процессов в исследуемой схеме.

Определим понятие переключающей функции. Переключающая функция принимает два зна- чения в зависимости от истинности условий:

1, условие истинно ,0, условие ложно .

H

Переключающая функция силового полупро- водникового вентиля равна единице, когда ключ открыт, и нулю в противном случае:

F sw ^— ^

1, ключ открыт 0, ключ закрыт.

Математическое описание выходного напряжения тиристорного регулятора напряжения

Реализация математической модели многозонного тиристорного РПН начинается с задания входных синусоидальных напряжений питающей сети:

Va — Um • sin(w • t - ф);

Vb — Um • sin (ш • t - ф - 22);             (3)

V — Um • sin (to • t - ф - y).

Далее задается принцип управления многозонным тиристорным регулятором напряжения, для этого по необходимости формируется структурная схема управления рис. 5. На рис. 5 u оп n^u оп _k - опорные сигналы пилообразной формы для управления регуляторами; u_M1 и u_M2 — модулирующие сигналы для задания угла управления группами управления тиристоров; К - компаратор; Р , - группа управления i -м регулятором. Реализация принципа управления многозонного тиристорного регулятора напряжения в соответствии с предложенной структурой начинается с задания законов изменения модулирующего и опорных сигналов.

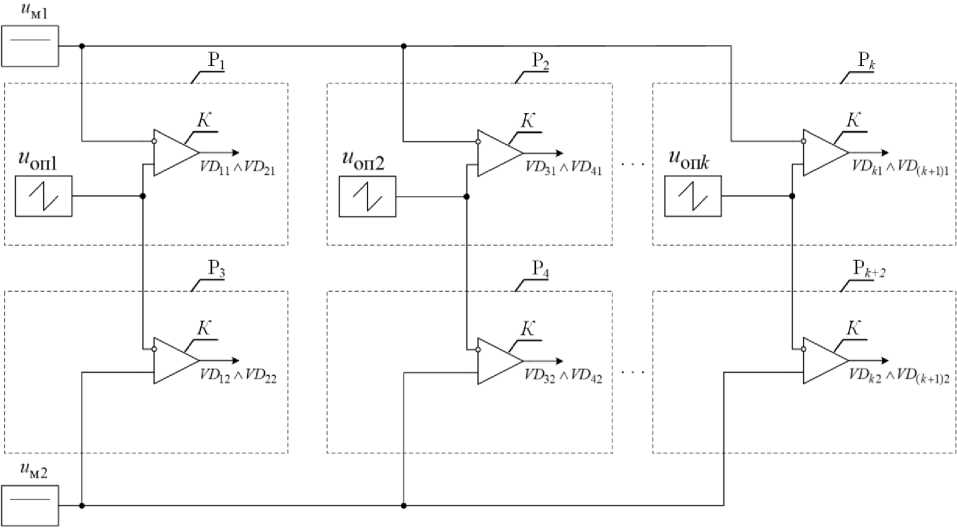
Рис. 5. Структурная схема для управления многозонным тиристорным регулятором напряжения

Закон изменения опорных сигналов при реализации данных математических моделей принят пилообразной формы, который описывается следующим образом [19]:

и опt = ^ • arctan [tan (to • t - 2 - ^^ + 1, (4) где i Е [1; к] - индекс описывающий номер фазы, к - количество фаз у регулятора напряжения.

Модулирующие сигналы задаются констан-

тами, пропорциональными углу управления:

Umi = constT;

иМ2 = const2.                               ( )

На рис. 6 представлены эпюры, поясняющие предложенный принцип управления.

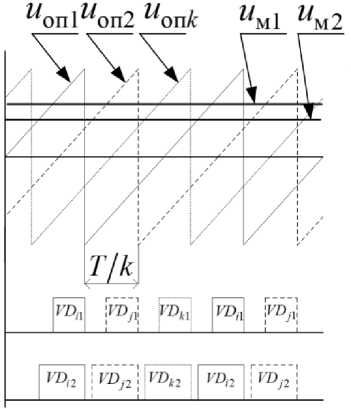
Рис. 6. Эпюры сигналов в системе управления

Далее происходит описание переключающих функций, определяющих моменты коммутации многозонного тиристорного регулятора напряжения, которые являются результатом работы сравнения опорных и модулирующих сигналов с помощью компараторов. Реализация имитируемых компараторов происходит за счет применения функции Хэвисайда или функции «signum», результат будет идентичным:

• ^Ft1 = ^Ф(и опt ^{- и} М1 ^);

F ti = 2 ^[sign⁽u опt — U mi ^)] + 2 ;             (6)

• ^Ft2 = ^Ф(и опt ^{- и} М2 ^);

Ft2 = 2 • [sign(uопt - Um2)] + 2.

Полученные переключающие функции определяют длительность включения соответствующей тиристорной пары и пропорциональны углам управления. При условии идентичности конденсаторов в теле регулятора и равенства напряжений на них выходное напряжение с учетом переключающих функций определяется следующими соотношениями:

4tr = Fii^2a + Fi2

Va.

2 ^;

V br =F 21^{/ V} 2 r +F 22

Vcr =F31^ + F32

'

Vb.

2 ^;

vc

■ —

.

Форма выходного напряжения представлена на рис. 7.

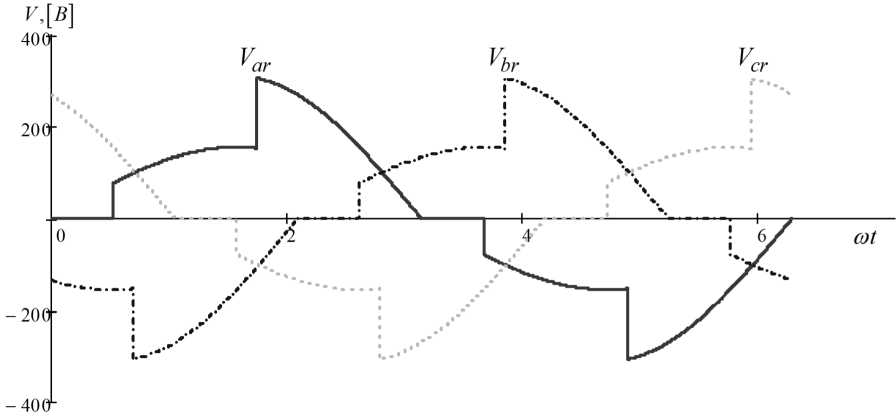
Рис. 7. Выходное напряжение многозонного тиристорного регулятора

Математическое описание тока нагрузки тиристорного регулятора напряжения

После того как было получено описание выходных напряжений, на следующем этапе построения моделей происходит этап математического формирования токов нагрузки тиристорного регулятора напряжения. Для определения токов многозонного тиристорного регулятора первоначально выполняется гармонический анализ напряжений. Для этого воспользуемся вычислением гармоник периодического сигнала выходных напряжений РПН через коэффициенты ряда Фурье. Для ускорения процесса расчета и повышения точности используются быстрые алгоритмы дискретного преобразования Фурье (ДПФ). Процедура дискретного преобразования Фурье описывает- ся следующим выражением:

2П

Hq^^/n^-^ ,          (8)

где Hq = Re(Hq^ + j • /m(Hq) - q-я гармоническая составляющая в комплексной форме, Nh - число отсчетов некоторой функции f(t) в дискретном представлении,/п - значение функции f(t) для отсчета и.

При использовании математических пакетов с возможностью выполнения быстрого преобразования Фурье (БПФ) по заданному числу гармоник, являющемуся степенью двойки, можно ускорить процесс вычисления гармонических составляющих с помощью операции БПФ:

С (f) = FFT(f), (9) где С (ид) - вектор-столбец из I элементов, которые являются гармоническими компонентами, представленными в комплексном виде: ReVC^+j^mVC^X

C(f) = RelC2(n]+j-Im[C2(f)] \Re[Cq(f)]+j4m[Cq(f)]]

Тогда амплитуды гармоник вычисляются следующим образом:

|C q (f)| = jRe[C q (f)]² + /m[C q (f)]².    (11)

В качестве функции f может быть массив дискретных значений любой периодической функции, напряжения, тока и т. п. Пользуясь инструментом БПФ, можно оценить коэффициенты гармоник.

Гармонический состав выходных напряжений, реализованный с помощью использования быстрого преобразование Фурье:

COW = 2FFT(V_ar);

C(V_br) = 2FFT(V_br);                   (12)

COM = 2FFT(VCr), где C(VaJ - вектор-столбец гармонических составляющих ряда Фурье в комплексной форме. Коэффициент «2» необходим именно вследствие комплексного представления ряда Фурье [20].

Получив гармонический состав выходного напряжения, определяют гармоники тока:

C q [i_a(V_a r )] = C q (V_ar)/qZ;

C q [i b (Vbr)A = C q (V br) /qZ;                 (13)

Cq[ia(Vcr)] = Cq(Vcr)/qZ, где z - комплексное сопротивление выходной цепи многозонного тиристорного регулятора. В случае активно индуктивной нагрузки z равно:

z = R_d+j_toL.                           (14)

Мгновенные значения тока находятся через обратное преобразование Фурье:

i_a = | /FFT[C[i_a(V_a r )]];

i b = 2 lFFT [C[i b (V br )] i c = 2 lFFT[C[i_a(V cr )A

Эпюра тока нагрузки трехфазного тиристор- ного регулятора на рис. 8. Сопоставления напряжения фазы А и тока данной фазы показано на рис. 9.

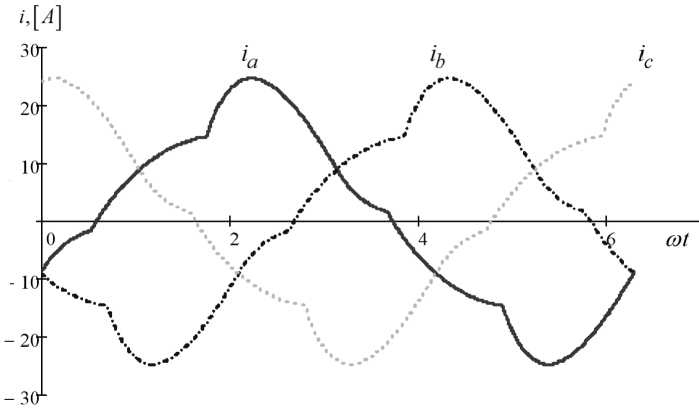
Рис. 8. Ток нагрузки трехфазного многозонного тиристорного регулятора

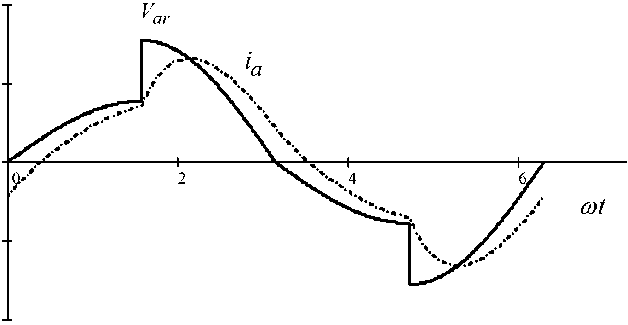
Рис. 9. Выходное напряжение и ток трехфазного многозонного тиристорного регулятора

Получив математическое описание фазных токов нагрузки, рассчитывают их средние и действующее значения, а также производят их гармонический анализ, пользуясь той же процедурой, что и для напряжения. Например, применим быстрое преобразование Фурье для тока фазы А : ■

C(i_a) = 2FFT(i_a).                         (16)

Зная вектор-столбец гармонических составляющих ряда Фурье в комплексной форме для фазного тока, рассчитывают коэффициент гармоник тока и интегральный коэффициент гармоник тока p -го порядка:

К гт = ^” = ₂(C_q(i_a))²/C i (i_a);           (17)

К ? = ^=₂(C_q(i a )/q^p • C i (i_a)).       (18)

Следующим шагом оценивается спектральный состав тока нагрузки многозонного тиристор- ного регулятора напряжения. Например, было отмечено, что в спектре тока нагрузки многозонного тиристорного регулятора присутствуют только нечетные гармоники [21, 22]. При увеличении углов управления происходит увеличение этих нечетных гармоник.

На рис. 10 представлен нормированный по первой гармонике спектр тока фазы A .

На рис. 11 показаны результаты моделирования в программе PSIM. Представлены выходное напряжение с током и входное напряжение с током во второй (верхней) зоне регулирования. Далее сопоставим эти результаты с результатами аналитического расчета. Предложенный математический аппарат позволяет определить коэффициенты гармоник токов и напряжений предлагаемых регуляторов, и тем самым можно оценить качество этих параметров. Так, коэффициент гармоник входного и выходного тока двузонного тиристорного регулятора переменного напряжения оценивается менее 5 %.

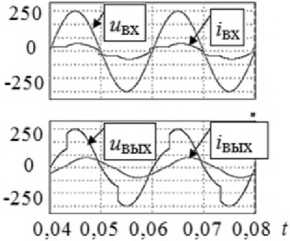
Рис. 11. Результаты моделирования однофазного РПН

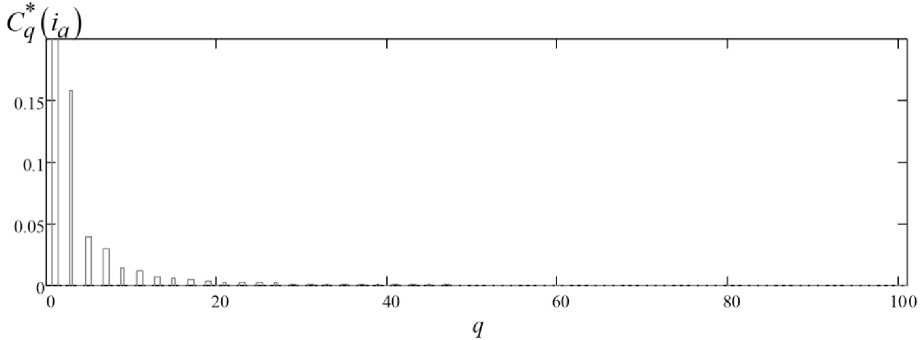
Рис. 10. Спектр тока нагрузки регулятора

Заключение

В данной работе был рассмотрен процесс создания математической модели для многозонного полупроводникового преобразователя, который выступает в качестве регулятора переменного напряжения. Данные регуляторы позволяют повысить качество выходного тока в устройствах плавного пуска, а также снизить величину броска пускового тока по сравнению с однозонными тиристорными регуляторами. Предложенные математические модели позволяют производить расчет электромагнитных процессов в установившемся режиме с меньшими затратами по временным и с меньшими требованиями к аппаратным ресурсам вычислительных комплексов по сравнению с существующими специализированными программными обеспечениями.

Работа выполнялась при финансовой поддержке РФФИ и Правительства Новосибирской области в рамках научного проекта № 17-48-543169.