Математическая модель для расчета характеристик сетей на базе коммутаторов Ethernet второго уровня

В статье разработана математическая модель, описывающая потоки на ветвях сети, построенной на базе коммутаторов Ethernet в виде системы нелинейных алгебраических уравнений. Приводится алгоритм решения системы уравнений при помощи итерационного метода.

Система уравнений для расчета сети при адресной рассылке кадров

В [1] приведены соотношения, позволяющие при фиксированных элементах матриц π и τ для заданной пары узлов k и l , рассчитывать ^ [ jk ^' l ) , 0 [ k ^ ' l ) , а также определять 2 j^kH(l ) — нагрузку на ветви сети, оказываемую процессом передачи кадров между этой парой узлов. На основании соотношений (1 )-(8) из [1 ] для каждой пары узлов k и l можно записать:

—[ к 1^( 1 )      . — [к 1^( 1) _х

У     = fv (У    ,п)

О ^[ k ' ) = f (О ^{[ к} ') ,т)

Я ^{[ к} ■) = Л (У ^[ k ■) , Л ) .

П у = f n (^ j ]^⁽ l ) )

T i = f T (^ jk ' ) )

Обобщая последние пять выражений, можно составить систему нелинейных алгебраических уравнений (СНАУ):

'T = f ₅ (T , n )

0 = f . ( 0, T )

< я = f _я (T , Л) ,            (1)

n = f п ( X )

. t = f т ( X )

где

UH(2)   —[ k H(l)   —[П и -1НЧ ).

^ = { ^      ,.., ^      ,.., ^         }

0 = {о" ” ') ,..,о ^{[ k} ] ^^{( l} ) ,.., о ^{[ n} u ' '") } .

2 = :/' ' ' ,.., 2 ^{[ k} ') ,.., 2 ^[n u         ) }

Типы уравнений, число уравнений заданного типа, типы и число переменных СНАУ представлены в таблице 1.

Таблица 1. Число уравнений и переменных в системе

Тип уравнений	Число уравнений	Число переменных типа
		v ^)	^ [k ] ^ ( l )	λ ij	π ij	T.. ij
T = f s (T,n)	n 2 u ⋅ ( П и - 1)	n 2 u ⋅ ( П и - 1)	0	0	r	0
0 = fe ( 0 , t )	n 2 u ⋅ ( П и - 1)	0	n 2 u ⋅ ( П и - 1)	0	0	r
2 = . fx (^, Л)	r	n 2 u ⋅ ( П и - 1)	0	r	0	0
π= f n ( 2 )	r	0	0	r	r	0
τ= f T (^)	r	0	0	r	0	r

Из приведенной таблицы видно, что число уравнений системы совпадает с числом переменных и равно ² • nu ² • ( n u ^- 0 + ³ • r ■

Алгоритм для расчета характеристик сети при адресной рассылке кадров

На рис. 1 приведен алгоритм, позволяющий рассчитывать характеристики качества обслуживания на сети, а также нагрузку, оказываемую на сеть при передаче кадров по сети по индивидуальному адресу. Этот алгоритм является составной частью другого алгоритма, используемого ниже для решения СНАУ.

Перед началом работы алгоритма считаются заданными следующие данные:

• -    число узлов сети;

• -    топология сети с учетом результатов работы алгоритма STa;

• -    нагрузка, которую необходимо передать по сети при адресной рассылке.

В результате работы алгоритма оказываются рассчитанными:

• -    вероятности доставки кадров между каждой парой узлов;

• -    время доставки кадров между каждой парой узлов;

• -    нагрузка, поступающая на ветви сети, а также задержки при передаче кадра по ветвям сети, вероятности их блокировок и уровни загрузки каналов.

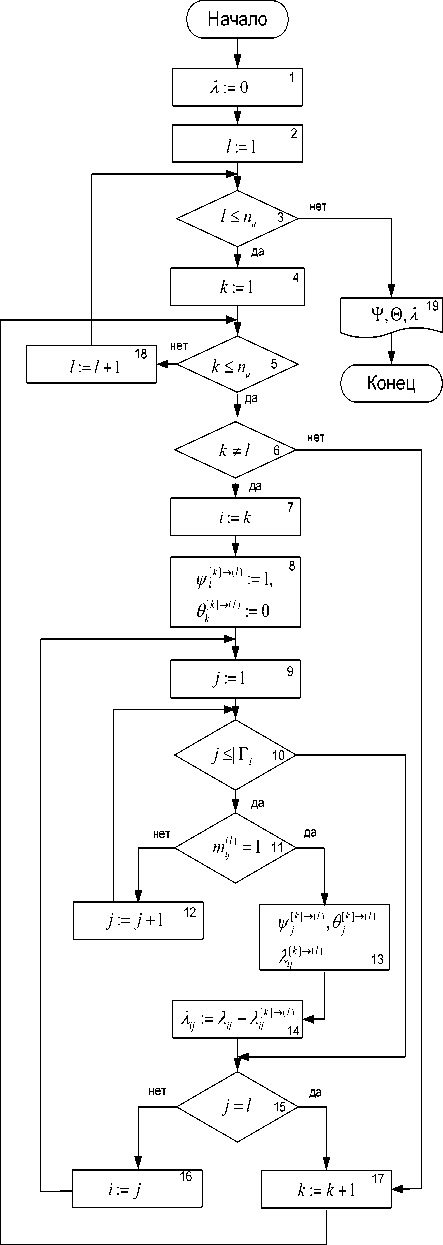
Рис. 1. Алгоритм расчета Ψ,Θ,λ при адресной рассылке кадров

Рассмотрим основные действия, осуществляемые в ходе работы алгоритма.

Вершина 1. Обнуляется матрица интенсивностей поступления потоков на ветви сети.

Вершины 2, 3, 18. Осуществляется перебор узлов, которые могут быть искомыми.

Вершины 4, 5, 6, 17. Обеспечивается перебор узлов, которые могут быть исходными. Поскольку один и тот же узел одновременно не может быть и исходным, и искомым, то при помощи вершины 6 исключается выполнение расчета для пар узлов, имеющих совпадающие номера.

При помощи вершин 7-16 осуществляется просмотр всех узлов, входящих в маршрут, начиная с узла k и заканчивая узлом l . Для самого первого узла, входящего в маршрут L ^{[ k} ^'l) , в вершине 8 присваиваются начальные значения для вероятности и времени задержки кадра. Эти значения равны для узла k соответственно 1 и 0. Номер узла j , следующего за узлом i в маршруте L ^{[ k} ^ 'l) , определяется в вершинах 9-12. Для просмотра соседей вводится переменная v , которая изменяется в диапазоне от 1 до |Γ _i | – числа соседей рассматриваемого узла i . В вершине 11, на основании маршрутных таблиц, определяется, какой конкретно узел-сосед является следующим в маршруте.

В вершине 13, используя соотношения 1, 4, 7 из [1], рассчитывается вероятность попадания в узел j для кадра, передаваемого по сети между парой узлов k и l , возникающая при этом задержка, а также нагрузка на ветвь ( ij ).

В вершине 14 нагрузка, создаваемая на ветвь ( ij ) передачей кадра между узлами k и l , добавляется к нагрузке, оказываемой на эту ветвь другими парами узлов.

В вершине 15 проверяется условие о том, является ли найденный узел j последним в маршруте. Если нет, то текущему узлу i присваивается номер j и для него производятся те же действия, которые были выполнены для предыдущего узла. Если же найденный узел оказался последним в маршруте, то есть его номер j = l , то расчет параметров для данной пары узлов k и l считается законченным. Переходим к расчету параметров для следующей пары узлов.

Заметим, что результаты работы этого алгоритма являются промежуточными, поскольку первоначально нам не были известны истинные значения элементов матриц π и τ . Более того, эти величины являются функцией от нагрузки λ , которая в свою очередь рассчитывается при помощи этого алгоритма. Расчет окончательных значений будет рассмотрен ниже.

Соотношения для расчета характеристик сети при широковещательной рассылке кадров

В [1] приведены соотношения, позволяющие при фиксированных элементах матриц π и τ для заданного исходного узла k рассчитывать £ vk ] , j ] , ^[k ] при передаче кадров в широковещательном режиме. На основании (11)-(13) из [1] для узла k можно записать:

—[ к ]        —[ к ]

£^[] = f (£ ^И,п),

• -[ к ]              [ к ] .

t = f t ^{( t , Т} X

х ^{[ k]} = f_x ( £ ^[k], h к ) , n = f n ( Х ^[к ] ),

T = f. ( X ^{[ к ]})

Обобщая эти выражения, можно составить следующую систему уравнений:

s = f ₃ ( s , n );

^T = f т ( ^T , т );

• f _x ( s , К ); ⁿ = ^f , ⁽^);

_^т = ^f _r ⁽^ )•

где

s	= { ^ [1] ,	.., # [k] ,.	., # [ n ■ ' i
T	= { t [1] ,.	. [ k ] ., t , ..,	t [ n u ] i,
X	= { X [1] ,	.., X [ k1 ,.	., X [ n u	' i

Типы уравнений, число уравнений заданного типа, типы и число переменных СНАУ представлены в таблице 2.

Таблица 2. Число уравнений и переменных в системе

Тип уравнений	Число уравнений	Число переменных типа
		^ i k ]	t [ k ] i	^ ij	π ij	T.. ij
E = f^ ( E , n )	n 2 u	n 2 u	0	0	r	0
T = f T ( T , t )	n 2 u	0	n 2 u	0	0	r
x = fx ( H , Й )	r	n 2 u	0	r	0	0
П = f n ( X )	r	0	0	r	r	0
T = f T ( X )	r	0	0	r	0	r

Из приведенной таблицы видно, что число уравнений системы совпадает с числом переменных и равно

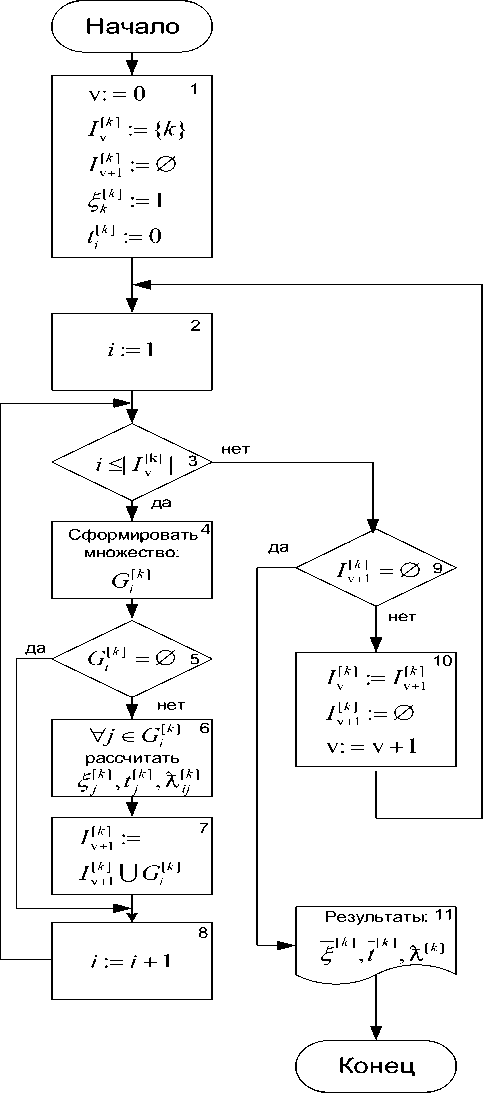
Рис. 2. Алгоритм расчета характеристик при передаче кадров в широковещательном режиме

Алгоритм расчета характеристик при передаче кадров в широковещательном режиме

На рис. 2 приведен алгоритм расчета характеристик сети при рассылке кадров в ши- роковещательном режиме. Перед началом работы алгоритма необходимо ввести или передать из других программ следующие исходные данные: топологию сети с учетом работы алгоритма STa, узел k, относительно которого идет просмотр, а также матрицы π и τ , содержащие вероятности блокировок и задержки при передаче кадров по соответствующей СБК.

Рассмотрим действия, осуществляемые в вершинах алгоритма.

Вершина 1. Поскольку кадр вводится в узле к , то §{ ^] = 1, t k ^{k ]} = 0. Поярусный просмотр начинается с узла к . Для этого во множество I V k ^] занесем узел k . Поскольку узлы первого яруса еще не просмотрены, делаем соответствую-

[ к ]

щее этому ярусу множество I ; _{+ 1} пустым.

Вершины 2-8. Осуществляется просмотр узлов v -яруса. Для каждого узла этого яруса, используя соотношения (9) из [1], формируется множество (вершина 4). Затем, используя соотношения (11)-(13), для рассматриваемого узла i рассчитываются ^ ^{{к ]} , t j ^] , Х \ ^{к ]} .

В ходе просмотра узлов v -яруса, используя соотношение (1 0) из [1 ], формируется множество узлов ( v + 1)-яруса (вершина 7). После того,как все узлы яруса просмотрены,анали-зируется сформированное множество узлов ( v + 1)-яруса - I V + (вершина 9). Если это множество пусто, то это означает, что все узлы сети просмотрены. В результате работы алгоритма (вершина 11 ) оказываются рассчитан-

—[k ] -[] ]

ными векторы £ , t , а также матрица Л ^{1 1}.

Если множество I V k + l не пусто, то переходим к просмотру узлов следующего яруса. Для этого необходимо выполнить действия, перечисленные в вершине 10, а именно: пере-

[ к ]          [ к ]

писать узлы из множества I ; ₊ 1 в 1 ; , очистить множество I V k + l , увеличить номер просматриваемого яруса v .

Перебирая k в диапазоне от 1 до n _u , можно [k ]     -[ к ]

рассчитать сначала векторы ξ и t , а затем и все элементы матриц Ξ и T .

Обобщенный алгоритм расчета характеристик

Ранее были рассмотрены два алгоритма, позволяющие при заданных задержках и вероятностях блокировок ветвей сети, рассчитывать характеристики сети для адресной и широковещательной рассылки кадров. Обычно эти два способа рассылки используются совместно. На рис. 3 приведен алгоритм расчета характеристик сети, в основе которого лежит решение СНАУ, которая включает в себя объединение систем (1) и (2). Работа начинается с ввода исходных данных (вершина 1), к которым относятся: nu – число узлов, Г – матрица смежности, с учетом работы алгоритма STa, Λ – матрица нагрузки, которую нужно передать по сети адресным способом, ft - вектор нагрузки для передачи методом широковещательной рассылки, μ – интенсивность обслуживания – величина, характеризующая длину кадров, С – матрица пропускных способностей каналов сети.

Затем начинается итерационный процесс решения СНАУ (вершины 3-1 0). Перед началом итерационного процесса необходимо задать начальные условия (вершина 2). В ходе каждой итерации запускаются процедуры расчета характеристик при адресной рассылке кадров (вершина 5), а затем – при использовании широковещательной рассылки кадров (вершина 6). Рассчитанные при этом нагрузки суммируются (вершина 7). После завершения каждой итерации,сравниваются значения потоков, рассчитанные на текущей и предыдущей итерациях (вершина 8).

Если расхождение меньше наперед заданной величины δ_max , то делается вывод о том, что решение найдено и выходим на выдачу результатов (вершина 11 ). В противном случае пересчитываются матрицы π, τ (вершина 9), и выходим на очередной цикл итерации.

Обычно итерационный процесс сходится за 3-4 итерации. Однако, в отдельных случаях, когда нагрузка, поступающая на сеть, превышает ее пропускную способность, значения элементов матрицы λ , полученные на соседних итерациях, будут всегда отличаться. Это означает, что итерационный процесс не сходится, а, следовательно, решение отсутствует. Физически это означает, что сеть не в состоянии пропустить поступившую на нее нагрузку.

Заключение

Рассмотренная в этой статье математическая модель позволяет рассчитать основные характеристики для сетей, построенных на базе коммутаторов Ethernet как при адресной передаче кадров, так и при использовании широковещательной рассылки. Результаты моделирования и их анализ предполагается привести в последующих публикациях.