Математическая модель для расчета характеристик термоэлектрических модулей охлаждения

В настоящее время термоэлектрические устройства находят применение в различных технических приложениях. Основные направления их использования – производство холода и преобразование тепловой энергии в электрическую. Наиболее широко термоэлектрические

Постановка задачи

Термоэлектрический модуль – тепловой насос, обеспечивающий теплопередачу от охлаждаемого объекта в окружающее пространство. Режим и характеристики работы ТЭМ зависят от теплофизических и термоэлектрических свойств материала, длины и сечения ветвей, рабочего температурного диапазона, плотности электрического тока или напряжения питания. Представленная математическая модель описывает процессы теплообмена в отдельной термоэлектрической ветви и предназначена для расчета характеристик и оптимизации конструкции ТЭМ. В модели учитываются эффект Пельтье, эффект Томпсона, перенос теплоты механизмом теплопроводности и джоулево тепловыделение. Теплофизические и термоэлектрические свойства материала учитываются в виде температурных зависимостей, сечение ветви может быть переменным по длине. Температурное поле по длине ветви с теплоизолированной боковой поверхностью описывается с помощью стационарного уравнения теплопроводности вида dp (S(x)Я(T) dT) = j(X)S(x)t(T) dT - S(X) j(x)2 p(T), dx          dx                 dx

где S(x) – сечение ветви как функция координаты x ; T – температура; λ ( T ) , τ ( T ) , ρ ( T ) –темпе-ратурные зависимости коэффициента теплопроводности, коэффициента Томсона и удельного сопротивления материала ветви; j(x) – плотность тока.

Граничные условия для уравнения (1) заданы на холодном спае ветви

C 0= T 0 , ^ dT ^x            dx

= a T j ₀ - Q 0 / S ₀,

x = 0

где α ( T ) – коэффициент термоЭДС; T 0 , j 0 и S 0 – температура, плотность тока и площадь поперечного сечения ветви на холодном спае; Q ₀ – тепловая мощность, поступающая на холодный спай. С горячего спая ветви во внешнюю среду отводится суммарная тепловая мощность Q 0 + W , где W – электрическая мощность, потребляемая ТЭМ.

Дифференциальное уравнение второго порядка (1) с помощью замены y=5 (*ж T                                                    (3)

dx преобразуется к двум обыкновенным дифференциальным уравнениям первого порядка

* = j ⁽ *^{) T (}T ) y - _x ( * ) j ( * ) , p (_T dx      Л ( T)

dT = y dx 5 (x )Л(Т)"

Для решения системы уравнений (3) – (5) использован метод Рунге-Кутта. Входными параметрами математической модели являются плотность тока, теплофизические и термоэлектрические свойства материала, геометрические размеры ветви. Перепад температуры на длине ветви может достигать нескольких десятков градусов; при такой разнице температур свойства материала могут существенно изменяться, поэтому для повышения точности расчетов теплофизические и термоэлектрические свойства необходимо задавать в виде температурных зависимостей.

Результаты математического моделирования и их обсуждение

На основе математической модели рассчитаны как локальные характеристики (распределение температуры по длине ветви), так и интегральные параметры: перепад температуры ∆ T , холодильный коэффициент полезного действия COP (Сoefficient Of Рerformance), определяемый как отношение холодопроизводительности к потребляемой электрической мощности Q ₀/ W . Расчеты проводились без привязки к определенным значениям электрической мощности и холодопроизводительности ТЭМ. В качестве термоэлектрического материала рассматривался теллурид висмута.

Характер распределения температуры и теплового потока по длине ветви зависит от режима работы ТЭМ. Из решения системы уравнений (3) – (5) получены зависимости T(x) , которые приведены на рис. 1 для длины ветви L = 1.6 мм и двух значений плотности тока: 100 и 200 А/см². На рисунке видно, что зависимость T(x) при j = 100 А/см² имеет монотонный характер, при j = 200 А/см² на кривой T ( x ) формируется максимум, обусловленный четырехкратным ростом мощности джоулева тепловыделения в объеме ветви при увеличении плотности тока в два раза.

Одним из важнейших параметров для анализа эффективности ТЭМ является холодильный коэффициент полезного действия COP. Значение COP зависит от эксплуатационных и геометрических параметров ТЭМ. Для определения оптимального режима электропитания были рассчитаны зависимости COP от плотности тока, которые представлены на рис. 2 для различных значений перепада температуры. Эти зависимости имеют максимумы, соответствующие им значения плотности тока оптимальны. Наличие максимумов связано с тем, что зависимость мощности джоулева тепловыделения пропорциональна ~ j ², а мощность термоэлектрического охлаждения ~ j ; таким образом, с некоторого значения плотности тока рост мощности джоулева тепловыделения начинает превалировать над эффектом Пельтье и эффективность охлаждения снижается.

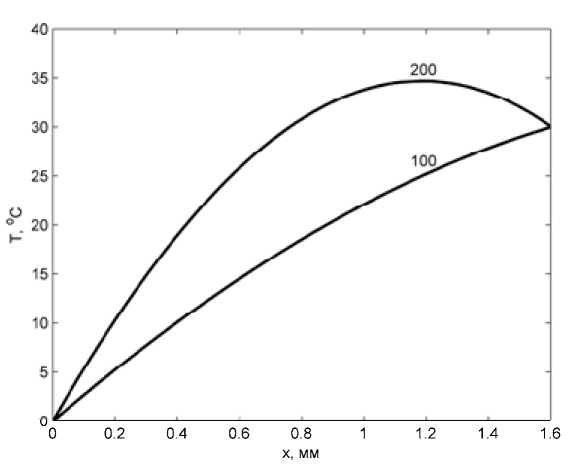
Рис. 1. Распределение температуры по длине ветви при j = 100 и 200 А/см²

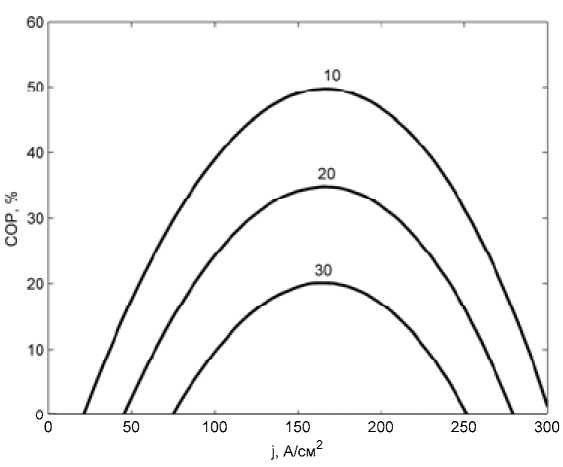
Рис. 2. Зависимости COP от плотности тока при значениях Δ Т = 10, 20 и 30 ºС

К геометрическим параметрам ветви, влияющим на эффективность охлаждения, относятся прежде всего длина и форма ветви (изменение площади сечения по длине). На рис. 3 приведены зависимости COP от длины ветви при различных значениях перепада температуры Δ Т между холодным и горячим спаями и постоянном значении поперечного сечения ветви. На графиках видно, что зависимости COP ^L) имеют максимум, положение которого зависит от значения А Т При уменьшении длины ветви, с одной стороны, снижается ее электрическое сопротивление – 1020 –

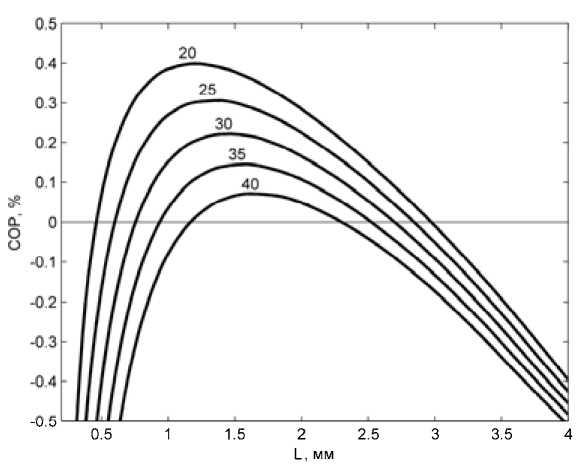
Рис. 3. Зависимость COP от длины ветви при значениях ΔТ = 20, 25, 30, 35 и 40 ºС и, следовательно, суммарная величина джоулева тепловыделения, распределенного в объеме ветви, с другой – уменьшается термическое сопротивление и возрастает тепловой поток за счет теплопроводности, поэтому существует некоторая оптимальная длина ветви термоэлемента, которую можно определить из этих графиков для каждого значения ΔТ. По данным зависимостям можно определять эффективность работы ТЭМ в различных температурных режимах и проводить оптимизацию конструкции в зависимости от его назначения (достижение максимального COP либо максимального перепада температуры).

В математической модели пространственная форма ветви может задаваться произвольным законом изменения S(x) . В представленном расчете площадь поперечного сечения ветви задавалась в виде линейной функции с помощью безразмерного параметра a , характеризующего степень изменения сечения ветви. Значения сечений ветви на холодном и горячем спаях определены в виде S 0 = S 1/2 (1 – a ) и S 1 = S 1/2 (1 + a ), при этом среднее сечение S 1/2 для всех a остается неизменным. В этом случае закон изменения сечения по длине ветви имеет вид S(x) = S 1/2 (1 +a (2 x / L -1)) (значения х = 0 и L относятся, соответственно, к холодному и горячему спаям). При значении a = 0 ветвь имеет постоянное сечение по длине, для a = 0,5 и a = -0,5 площади сечений S 0 и S 1 отличаются в 3 раза. Расчет проведен при значениях j = 150 А/см² в среднем сечении ветви и L = 1,6 мм. На рис. 4 приведены графики COP( a ) для трех значений перепада температуры – 10, 20 и 30 ºС. Из полученных зависимостей видно, что наибольший COP достигается, когда сечение ветви имеет некоторое расширение к холодному спаю ( a ≈ -0,12). Наличие максимума, смещенного в область отрицательных значений a , связано с двумя факторами. С одной стороны, тепловой поток при приближении к холодному спаю возрастает за счет прироста распределенной в объеме ветви джоулевой диссипации, таким образом, расширение площади поперечного сечения ветви способствует более эффективной передаче увеличивающейся тепловой мощности. С другой стороны, при расширении сечения – 1021 –

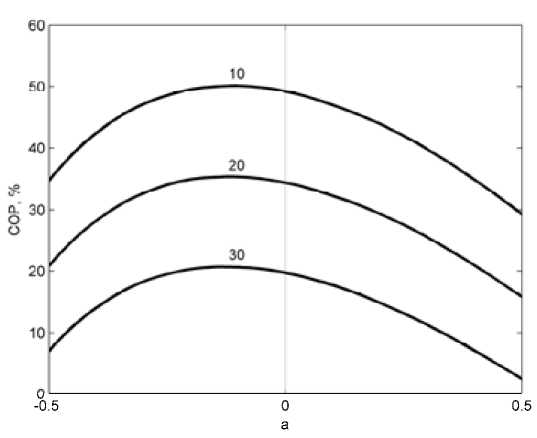
Рис. 4. Зависимость COP от степени изменения сечения ветви ветви у холодного спая приводит к уменьшению j и, следовательно, COP (в соответствии с рис. 2).

Результаты расчетов COP, приведенные на рис. 2-4, показывают возможность оптимизации конструкции, режима работы и достижения максимальной эффективности ТЭМ по таким исходными параметрам задачи, как плотность тока, длина и форма термоэлектрической ветви. В свою очередь, задание поперечного сечения ветви и количества ветвей в конструкции позволяет определить силу тока, напряжение электропитания и холодопроизводительность ТЭМ.

Одной из важнейших характеристик ТЭМ являются зависимость COP от различных температурных условий. На рис. 5 отражены расчетные зависимости COP от перепада температуры на ветви A T при различных значениях температуры холодного спая для j = 150 А/см², L = 1,6 мм и постоянного сечения ветви. Следует отметить, что данные параметры не являются оптимальными для достижения в ветви максимального перепада температур или холодопроизводительности, представленные графики прежде всего показывают влияние температурных условий на величину COP. На рис. 5 видно, что режим максимального COP возможен при малых перепадах температур, наоборот, при максимальном перепаде температуры COP близка к нулю. При снижении температуры холодного спая величина COP существенно уменьшается. Для заданной конструкции ТЭМ по зависимостям COP могут быть рассчитаны зависимости холодопроизводительности от силы тока. Производители серийных ТЭМ обычно приводят нагрузочные характеристики, которые являются зависимостями холодопроизводительности Q(ATI) при определенной температуре горячего спая и нескольких значений силы тока. Нагрузочные характеристики служат основой для математического моделирования, анализа рабочих режимов и разработки термоэлектрических систем охлаждения [3, 4].

Таким образом, математическая модель позволяет получить зависимости холодильного коэффициента полезного действия от длины и формы ветви, перепада температуры между холодным и горячим спаями, плотности тока и температуры охлаждения для термоэлектрическо- – 1022 –

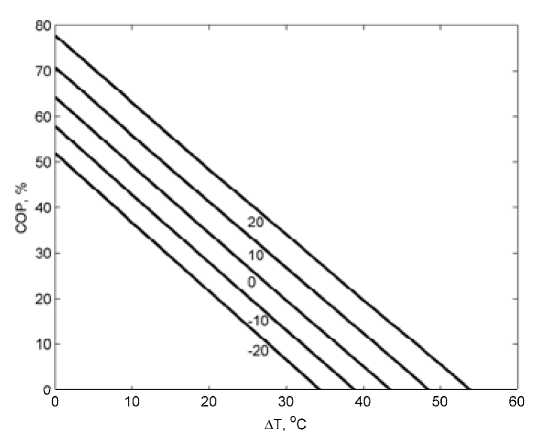
Рис. 5. Зависимость COP от перепада температуры ∆T при различных значениях температуры холодного спая го материала с известными теплофизическими свойствами. На основе этих данных выбирают оптимальные конструктивные параметры и режим работы ТЭМ с учетом его функционального назначения. Кроме того, исходя из технических требований по холодопроизводительности и напряжению питания определяют сечение и количество ветвей, а также габариты ТЭМ.

Заключение

Представленная математическая модель позволяет рассчитывать все основные локальные и интегральные характеристики ТЭМ с учетом температурных зависимостей теплофизических и термоэлектрических свойств материалов. Результаты расчетов позволяют проводить оптимизацию конструкции и определять требования к эксплуатационным параметрам ТЭМ. Математическая модель может быть использована как составная часть расчетных теплофизических моделей термоэлектрических систем охлаждения различного назначения.