Математическая модель движения корнеплода по ротационному гофрощеточному рабочему органу

Введение. Нами разрабатывается устройство щёточного типа для сухой (безводной) очистки кормовых корнеплодов при подготовке их к скармливанию сельскохозяйственным животным. Основу разрабатываемой нами конструкции составляют рабочие органы в виде четырех наклонно расположенных вращающихся щеточных барабанов, набранных из комплектов рабочих элементов криволинейной (гофрированной) формы «пильчатого» профиля, изготовленных из капрона, эластана или резины [1, 2, 3]. Актуальность проводимых нами исследований обуславливается тем, что скармливание сельскохозяйственным животным кормовых корнеплодов в неочищенном виде не эффективно, т.к. это приводит к желудочным забо леваниям животных и снижению продуктивности скота [4].

В настоящее время ведется научноисследовательская работа по усовершенствованию существующих и созданию новых способов и технических средств для безводной (сухой) очистки кормовых корнеплодов перед закладкой их на хранение или перед скармливанием сельскохозяйственным животным. Общие вопросы движения плоских и сферических частиц довольно подробно рассмотрены в трудах известных учёных в области прикладной земледельческой механики П.М. Василенко и П.М. Заики [5, 6]. Их теоретические разработки, с уточнением для конкретных условий, позволят получить математическую модель движения тела в форме полу- сфероконуса по наружной поверхности наклонного вращающегося цилиндрического гофрощёточного барабана.

Методика исследования. В связи с отсутствием основных аналитических зависимостей для теоретического расчета гофрощеточного очистителя кормовых корнеплодов необходимо построение математической модели движения единичного корнеплода в форме полусфероконуса по наружной поверхности цилиндрической вращающейся гофрощётки. Построение математической модели производим путем получения системы нелинейных дифференциальных уравнений динамики движения корнеплода по поверхности гофрощеточного барабана и дифференциального уравнения вращательного движения корнеплода вокруг собственной оси в цилиндрических координатах и её численного встроенных функций математического калькуляционного пакета MathCAD Professional 2001 на ПК [7].

Результаты и их обсуждение. Процесс очистки корнеплодов гофрощёточным устройством осуществляется вследствие контакта головок единичных корнеплодов с поверхностями наклонных вращающихся цилиндрических гофрированных щёток. При этом за счёт принудительного вращательного движения гофрощёток и организации цикличного движения корнеплодов по их поверхностям осуществляется счёсывание связанных с корнеплодами примесей (налипшей почвы и растительных остатков).

Для построения математической мо- дели движения единичного корнеплода по наружной наклонной поверхности цилиндрической гофрощётки рассмотрим экви интегрирования с помощью метода Рунге- валентную схему движения корнеплода по

Кутта 4-го порядка точности. Численное

её поверхности, представленную на рисун-

интегрирование системы дифференциаль- ке 1. ных уравнений производим с помощью

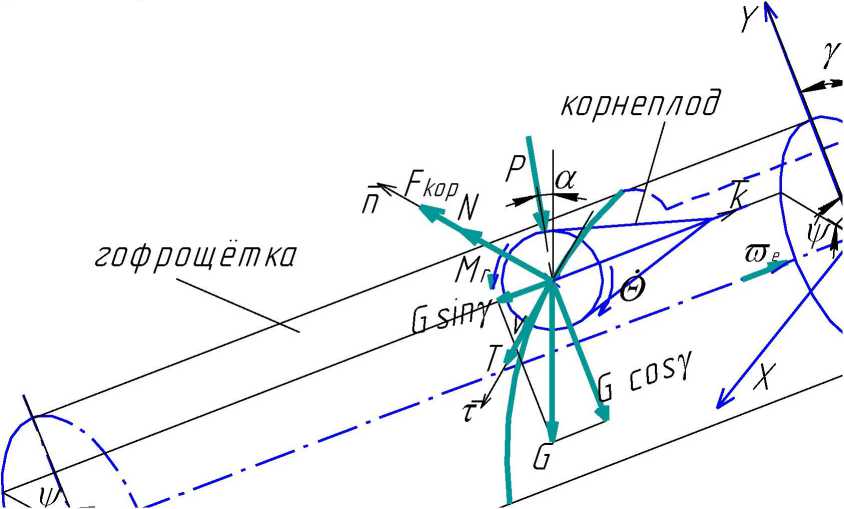
Рисунок 1 - Эквивалентная схема движения корнеплода по наружной поверхности вращающейся наклонной гофрощётки

Рассмотрим относительное движение единичного корнеплода. Примем в первом приближении, что модель корнеплода образована объединением двух геометрических объектов - полусферы и конуса - по радиусу г в широкой части. Гофрощетка наклонена к горизонту под углом у к гори зонту, имеет радиус R (рисунок 1) и вращается с постоянной угловой скоростью со. Допустим, что начальная скорость корнеплода при попадании на гофрощётку будет равна нулю, а окружная скорость гофрощётки будет всегда больше окружной скорости движения г, корнеплода по ней. При этом на корнеплод при движении будут действовать следующие силы:

G = nig - сила тяжести корнеплода массой т;

N - нормальная реакция поверхности гофрощётки, направлена по нормали к тра- ектории относительного движения тела;

Т = fN - сила трения скольжения корнеплода по поверхности гофрощётки (полезная сила счёсывания);

здесь /- коэффициент сопротивления движению тела в среде податливой гофрощётки, имеющей разрывы [8]: когда окружная скорость гофрощётки больше окружной скорости корнеплода по ней, сила Т направлена в сторону вращения гофрощётки [6];

Ғкор =2m co vr sin(co''vr) - сила Кориолиса, направлена по нормали к траектории относительного движения корнеплода;

Р = (2ⁿ-l) mg 2cosa - сила давления п вышележащих корнеплодов, а - угол между линией, соединяющей центры корнеплодов, и вертикалью (для шарообразных в сечении тел а = 30 °);

М_г =дМ=тХ£ p-N - момент силы трения качения, где 5 - коэффициент трения качения, // - угол трения качения.

Введём абсолютную неподвижную систему координат XYZ с началом в точке О (рисунок 1), причём ось OZ направлена параллельно продольной оси гофрощётки, а ось ОХ направлена в сторону относительного корнеплода. Применим также относительную систему координат, задаваемую ортами т, п, к, жёстко связанную с вращающейся гофрощёткой [6]. Для определения положения тела на гофрощётке в любой рассматриваемый момент времени используем также цилиндрическую систему коор-

■■                                 z                                            >             P (S'-til mp ф = my cosy sin^r 4- P (cos a cosy sin^? 4- sin a cos^rj 4- fN . '     ;=

^(ф-ш) +г!

динат z и у, где у - угловой параметр, отсчитываемый от вертикальной оси (рисунок 1).

Тогда выражение для абсолютной скорости движения корнеплода 1^ имеет вид:

/■ = г = ру/т + zk,       (1)

где р - радиальный параметр положения центра тяжести корнеплода относительно оси гофрощётки.

Продифференцировав (1) по времени, получим выражение для абсолютного ускорения тела:

w_a = pwr +рц/" n + zk.     (2)

Основное уравнение динамики движения корнеплода по поверхности гофрощётки в векторной форме имеет вид:

kor

Для определения проекций внешних сил на оси подвижной системы координат необходимо найти относительную скорость тела vr = va — vb , где PQ - абсолютная скорость движения тела; Vb = раус - переносная скорость тела. С учётом (1) составим выражение для относительной ско- роста тела в виде Vr = р Щ—а) T + zk или

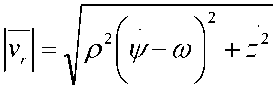
С учётом (1), (2) и (4) после некото-преобразований основное уравнение

рых динамики в цилиндрической системе координат примет вид:

I— ---~— mp ip" = P(sinc sin^ - cos a cosy cos^) + JV + Ims^p2^ - m) + mz = mg sin у 4- P cos a sin у — fN .      = z2siny — mg cos y cos ^ . (5)

^р5(ф-у} +5=

Кроме того, запишем дифференциальное уравнение вращательного движения корнеплода вокруг собственной оси:

‘ ie = Tr-Mr=JNr-6N=(fr-d)N, (6)

где I - момент инерции корнеплода относительно центральной оси.

Для корнеплода в форме полусферо-конуса[7]

I = m г2(Ъ1к + 8/^ 10(7^4- 2г), где 1к - длина конусной части корнеплода.

1—Л^р2ф2 +z2

С учётом (7) получим следующую систему дифференциальных уравнений дви- жения корнеплода по наружной цилиндрической вращающейся гофрощётке:

у/ = 0.5 — cos у sin у/ + — (cos a cos у sin у/ + sin a cos у/) + Л^р²у² + z²ip + ' р               тр            ’                            ‘

Ш

, 7^          P(sin a sin у/ - cos a cos у cos у/) + Im со sin yJp4>^-

^p^y-mf+z1 Г

•2.

- mg cos у cos у/] -

— cos у sin у/ + -^- (cos a cos у sin у/ + sin a cos у/) + A^p2ip2 + z2ip + р        тр н--.                  P(sina sin у/-coSa cos у cos у/)+ 2/7/о sin уд//?2 (у/-®)2 + z2 -

Шл]pv^ip - o')² + Z²

- mg cos у cos

i//]] -4 A^p²ip² +z²y/(—cos у sin у/ +-^-(cos a cosy siny/ + sina cosy/)) - " '          p              mp           ’     '

/(y>-®)y>

P-^ рЧу - ®V" + z²

f g sin у + — cos a sin у |(1 - Adp²w² + z²)--,                [p(sin a sin у/ -

I m _________?_______________ ' m-jp² (yc — a>)² + z² _____________

1-Л^р²ір² +z² +

• -    cos a cos у cos y/) + Imo sin уд//?²(у/-®)² + z² - 777g cos у cos y/J

  
  

Р^рЧ^-^Ү+г2

10(^- -8^_k + 2r) P(sin a sin у/ - cos a cos / cos y/) + Im co sin уд//?² (у/ - ®)² + z² - " mr²^l_k + 8r)                    I-I^PV² +z²

• -    mg cos у cos у/

  Система уравнений (8) описывает движение корнеплода в форме полусферо-конуса по наклонной вращающейся гофрощётке. В связи со значительной нелинейностью данной системы её интегрирование выполнено численным методом Рунге-Кутта 4-го порядка точности с помощью встроенных функций математического калькуляционного пакета MathCad Professional 2001 на ПК. Данный метод является более совершенным и позволяет при меньшем объёме вычислений получать более точный результат. Метод Рунге-Кутта обладает значительной точностью и, несмотря на свою трудоемкость, широко используется при численном решении диф

ференциальных уравнений и систем. Важным преимуществом этого метода является возможность применения переменного шага, что позволяет учитывать локальные особенности искомой функции.

В современных программах, реализующих методы Рунге-Кутта, обязательно используется некоторый алгоритм автоматического изменения шага интегрирования. На участках плавного изменения решения счет можно вести с достаточно крупным шагом. На участках, где происходят резкие изменения поведения решения, необходимо выбирать более мелкий шаг интегрирования. Изменение шага для методов Рунге-Кутта сложности не представляет. Оценить погрешность достаточно сложно, так как простые способы оценки погрешности отсутствуют.

При сравнении результатов расчёта скоростей и перемещений корнеплода с шагами интегрирования Л=100иЛ = 50 погрешность метода составила не более 7%. При численном интегрировании в пакете MathCad примем постоянными следующие величины: угловая скорость гофро-щётки со = 20,93 с"1, масса корнеплода т = 2 кг, коэффициент сопротивления движению /= 1,49, угол наклона гофрощёток к горизонту у = 3°, сила давления от веса вышележащих корнеплодов Р = 79 Н, радиальный параметр р = 0,25, параметр X = 16,6 со следующими начальными условиями: угол контакта корнеплода с гофро-щёткой уо= -0,5236, угловая скорость корнеплода уо = 0,01 с"1, путь корнеплода zo= 0,01 л/, линейная скорость zo = 0 м/с. По полученным данным построен график изменения угловой со и линейной г скорости движения, а также перемещения 5 корнеплода вдоль гофрощётки (рисунок 2).

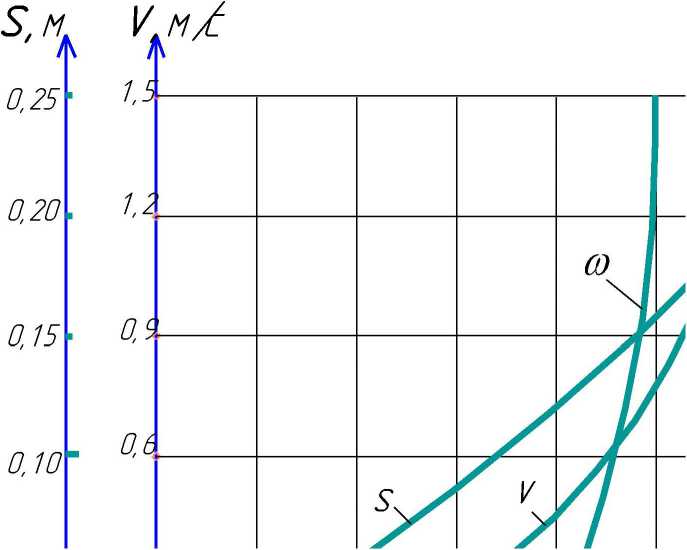
Рисунок 2 - График изменения угловой со, линейной г скорости движения и перемещения 5 корнеплода вдоль гофрощётки

Как показывают полученные графики, на протяжении всего времени контакта линейная скорость движения и путь, пройденный корнеплодом от начала отсчёта вдоль гофрощётки, монотонно возрастают. Угловая скорость перемещения со = f(t) изменяется по экспоненциальной зависимости, достигая максимальных значений после 1 = 1,8 с (при постоянной угловой скорости вращения гофрощетки co2iti= 20,93 с"1). В момент, когда угловая скорость движения корнеплода становится больше угловой скорости гофрощётки (1 = 1,8-2,4 с), тело отрывается (покидает рабочую поверхность). Наибольшее влияние на угло вую скорость движения и угол отрыва корнеплода оказывает угловая скорость вращения гофрощётки. На линейную скорость перемещения корнеплода и пройденный путь наибольшее влияние оказывает угол наклона гофрощёток к горизонту.

Выводы

• 1.    Предложены новые математические зависимости, позволяющие на основе полученных дифференциальных уравнений движения корнеплода обосновать основные параметры гофрощёточного очистителя.

• 2.    Установлена аналитическая зависимость кинематических характеристик

движения корнеплода вдоль гофрощётки (скорости, ускорения и перемещения) от основных конструктивно-технологических параметров устройства и физико-механических свойств очищаемых корнеплодов: частоты вращения и угла наклона гофро-щёток, силы давления вышележащих корнеплодов, геометрических размеров гоф-рощетки и корнеплодов.