Математическая модель движения одиночной сферической частицы люпина в экстракторе с помощью низкочастотных механических колебаний

Последние оказывают значительное влияние на характеристики гидромеханических, массообменных и иных процессов, что следует учитывать при расчётах экстракционных аппаратов.

Принятые допущения:

• 1.    При гидромодуле 1:6, каким он был в наших экспериментах, концентрация частиц люпина мала и их взаимным влиянием можно пренебречь, то есть движение каждой частицы можно рассматривать вне зависимости от движения остальных частиц. Траектория частиц будет очень сложной (хаотической).

• 2.    При определении соотношения между интенсивностями хаотического движения сплошной и диспергированной фаз принимаем, что размер частиц люпина в виде крупки существенно меньше по сравнению с масштабом минимальных турбулентных образований, то есть с наименьшей длиной волны турбулентного движения.

Хаотическое движение совокупности частиц твердой фазы в аппарате подтверждалось поведением меченых частиц.

Уравнение движения одиночной частицы приводят С. Соу, И.О. Хинце, С.М. Чен. И др. И.О. Протодьяконов записал его в виде [3]

для ускорения так называемой присоединённой массы частицы, обусловленной тем, что движущаяся частица вовлекает в движение окружающую её сыворотку. Четвёртый член учитывает влияние нестационарности течения на движение крупки (сила Бассэ). В целом правая часть характеризует полную силу, действующую на частицу в потоке.

Поскольку считается, что частица не влияет на движение, из (1) градиент давления можно исключить. Используя уравнение Навье – Стокса, описывающее движение жидкой фазы [2]:

(и V) и = —1Vp + vAU , ρ где и - вектор скорости; Au - оператор Лапласа; v - кинетическая вязкость жидкости, v = ц / р, из уравнения (1) получается следующее равенство:

1     3     d to 3     , /

—n d p_P —^L =— nv d p l to , 6 dt 4

1 ,з ( dto dto

+ —n d p l —^L + to —^L — v

6 Id t        k

1       . d L

+— n d p— 12

—

dt

d х.

k

, ^{— to} P ) ⁺

5² to . ) --------- 1 + д X k d X k }

^ + ³ d² p^ j di t ₀

t

d d5" — toP

- dt ' ,

—

1    ,3     d top-

—nd pp---■

6 ^Pdt

= 3 nv d _P ( to , - to p,

1, 3 d p     1     ,3 ^d ( to

—nd — +— nd p—-—

6       d x , 12             <

-

dt

®p )

— +  (1)

d

~         t — to — top

3 ^t iP i

+— d ² pnv dtp

2 t t ₀

— t ‘

- dt ‘ ,

где to_p, , p _P - , -я составляющая скорости частицы и её плотность; to , , p- , -я составляющая

скорости жидкости и давление в точке пространства, в которой находится частица в момент времени t; v - вязкость жидкости.

Уравнение (1) справедливо при достаточно малой относительной скорости движения частицы и окружающего её экстрагента. Поэтому принимаем, что дисперсные частицы на движение сплошной фазы не оказывают влияния, то есть значения величины to и p считаются равными тем значениям, которые имели бы месть при отсутствии в аппарате твёрдых частиц.

Проанализируем уравнение (1): левая часть уравнения представляет собой силу, которая необходима для ускорения частицы, то есть произведение массы крупки на её ускорение. Первый член правой части – сила вязкого трения, второй – сила, возникающая вследствие неравномерного давления вокруг частицы. Третий член представляет собой силу, необходимую

В уравнении (2) правая часть в совокупности представляет собой силу, действующую на частицу. Её правомерно считать случайной силой. Это справедливо, учитывая сформированные выше допущения применительно к турбулентной обстановке в экстракторе.

Уравнение (2) справедливо для мгновенных значений величин и оно приемлемо для нахождения статистических характеристик хаотического движения фаз. Для получения замкнутой системы уравнений можно использовать допущение о сравнительной малости нелинейных членов уравнения (2). В результате ряда преобразований выписано более простое уравнение, описывающее движение дисперсной частицы

1 Sto, 3 d to- 18 v/

Y +--^ =--^L + —т to

2 d t    2 d t     S ^{2 v} '

+9 Пj t0

d (to — to)

dt p’

^{— to} P ) ⁺

t — t'

dt ' ,

где у = p _P I p .

Статистическая связь соответственно между значениями скорости в моменты времени t 1 и t для дисперсной частицы, дисперсной частицы и сплошной фазы, а также сплошной фазы характеризуются соответственно тензорами временной корреляции:

Q f ( t 1 , t ) = ^to p, ( t 1 ) ^to p, ( t ) , ^P j. ( t 1 , t ) = ^to p, ( t 1 ) to ( t ) ,

R i. ( t 1 , t ) = ^to p, ( t 1 ) to ( t 1 ) .

В этих формулах черта означает операцию статистического осреднения.

Умножая почленно уравнение (3) на ® _p. ( t 1 ) и на ® , ( т 1 ) , а также осредняя, получим:

Используя изложенную процедуру вычислений, последний член уравнения (7) примет вид: 9 '2^ I d ® e_nr ( 1 — ‘ ) ( — ' ^) [ j ( ® ) " P i ⁽ ® ) ] . (8)

1 ] d г х 3 d _п / х

^{Y +} 2 J FQ ' ⁽ ' ) = 2 ds ^P * ⁽ ' ^{)+ +}р т [ P ⁽ ' ) - Q j ( ' ) ] ⁺

Учитывая уравнения (8) и (9), можно заключить, что каждое из уравнений (6), (7) представляет собой равенство двух интегралов Фурье, откуда следует равенство преобразований Фурье. Поэтому получаем:

9 Frd⁷ [ ^{P (} ' ') - Q« ⁽ ' ’) ] ⁺ d к —”   VF7—

ds ';

1 ) d _ / x 3 d _n / x Y + — —Qu ( ' ) =— R ( ' )

2 J ds i ( ) 2 ds j ( )

—

— 1 V [ R ( ' ) — P ( ' ) ] +

¹ Y ⁺ 2 J Q i ( ® ) = 2 ^p , ( ® ) ⁺ id⁸ ® [ P i ( ® ) - ^Q . ( ® ) ] ⁺

⁺ 1^{V ( 1 +} ' ) [ P i ⁽ ® ^{)— j (} ® ) ] ^;

Y +    P,. (® = 3 R_ti (® — ' -8 ^ 1 R„ (® — p ( ® 1 +

(     2 J ^yV ’ 2 ^yV ’ d²®^{[ jV ,jV 7]}     (-о)

⁺ 7      ^{( 1} — ' ) [ ^{p (} ® ^{)— p (} ® ) ] .

(®

”~[ RU ')- P/(s ')1 ₊9 V r ds ' ^[ j ⁽ ) i ^{( )]} d V n ^J        Q s — s '

ds '.

Здесь s = t – t 1 , s' = t' – t 1 , s и s' – переменные.

Вместо тензоров Р ij , R ij , Q ij подставляем в уравнения (4) и (5) их разложения в интеграл Фурье. Тогда получим:

Теперь из уравнения (9) и (10) исключаем тензор P . ( ® ) . После этого получим соотношение, которое связывает преобразования Фурье тензоров временной корреляции сплошной и диспергированной фаз:

p ( ® ) = Г ( ® ) Q . ( ® )          (11)

”

”

”.

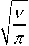
d d e e — ' s ( — i ® ) | y

2 П —”     ^v \

1 Y~,

⁺ ^ J P ⁽® ) =

- i ® s

— i

| 2 ^(— i ® ) p ⁽® )⁺ 18 г [ P ⁽® )^— p ⁽® ) ]j ⁺

Г ( ® ) =

"   1  9 V" _Y+2+dV2®_ 2 + " 2 V+1v" d22® d2® 2 з + 2 V12 +[2 V+—V

2 d V2 ®      d N 2 ® d² ®

+— d

”

J

—”

J ® e - ® ( — i ® ) [ j ( ® ) — j ( ® ) 1 ;

V s — s —” \_F             ^u                 -¹

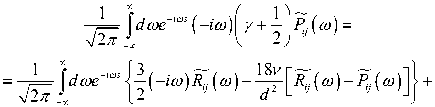
+ 9 V ” I      I ® e — ® • ( — i ® ) [ p ( ® ) — p ( ® ) 1 .

^d V r —” Fs — s —” V2 n

Меняя порядок интегрирования и вводя новую переменную t = s – s', последний член уравнения (6) запишем иначе:

9£ J T T e — ' ® ' ( — i ® ) [ P ( ® ) — , ( ® ) 1 J d T ^e ”

d V — —•” V2 n                       ^J0 T

Вычислим последний интеграл в этом уравнении, используя известные значения определённых интегралов [1]:

И.О. Хинце [4] установил, что интенсивности хаотического движения сплошной и диспергированной фаз, соответственно, определяются соотношениями:

I ² = ®® ( t ) , I P = ® pi ( t ) ^пР^и ' = ^1,2,3.

Эти соотношения можно переписать иначе, если учесть определения тензоров временной корреляции R . ( s ) и Q . ( s ) [3]

”

J

d T

—;= cos ®T

” d T

I —^sin ®t = V n / 2 ® . a/T

0 V ^T

Тогда этот член принимает следующий вид:

7 J V 17 ® e i ® ' ^{( 1 +} i ) ( ^— i   ) ^{[ Pii (} ® ^{) — j (} ® ) ¹ .

d 2

—”

1”

12i= R'i( 0) = T J R'(®) d®;(13)

—”

1” ~

Ip= Qi' (0) =      J Qu (®)d®.(14)

V 2 n —”

Выражая (13) через величину R _u ( ® ) согласно найденному соотношению (12) для интенсивности хаотического движения сплошной фазы имеем:

1     ”

I ; i- =-7t=J ^г ( ® )Qu ( ® ) d ® .      ⁽¹⁵⁾

—”

Определим явный вид этого соотношения. И.О. Хинце с достаточной точностью выразил тензор временной корреляции следующей формулой:

Q_H( s ) = i> "  " is ¹,              (16)

где λ – некоторые постоянные.

Находим преобразование Фурье этой функции:

a = i2i     .          (17)

nA i + to

Пренебрегая силой Бассэ (последний член правой части уравнения (1)), для функции Г(ω) получим:

Г ( ® ) =

i Y

Y +

2 J

+

18 У d² to J

9 ( 18 v У

+ I I

4 ( Id ² to J

Выражая в соотношении (16) величины

Q i ( to ) и Г(ю), согласно (17) и (18), после неко-

торых вычислений имеем:

_I 2 _fi

_I 2 _pi

2 )

A i d²

27 v

A i d ² 1 +

12 v J

где I ² _fi и I _p ² _i – интенсивности хаотического движения сплошной (жидкой) и диспергированной (твёрдой) фаз.