Математическая модель движения пульсирующего слоя вязкой жидкости в канале с упругой стенкой

С движением слоя жидкости в плоском канале приходится сталкиваться при исследовании широкого круга проблем, связанных с нормальным функционированием системы охлаждения и подачи топлива в двигателях аэрокосмических систем, а также в энергетике и гидроприводах сложных механических систем, используемых в авиационной и космической отраслях [1–3]. В большинстве случаев ограничиваются рассмотрением стационарного движения жидкости в канале, образованном абсолютно твердыми стенками. В [4, 5] рас- смотрены случаи движения слоя вязкой несжимаемой жидкости в канале с абсолютно твердыми стенками в рамках теории гидродинамической смазки. В то же время актуальными являются исследования причин и условий возникновения кавитации в жидкости, находящейся в канале. Например, в работах [6, 7] представлено исследование кавитации в охлаждающей жидкости двигателей внутреннего сгорания. В [6] экспериментально обосновано, что основной причиной вибрационной кавитации является упругая податливость стенок канала, и рассмотрены колебания стенки канала как свободные колебания цилиндрической оболочки без учета ее взаимодействия с жидкостью. В работе [7] исследование причин возникновения кавитации рассмотрено на основе решения задачи взаимодействия упругой балки-полоски с идеальной жидкостью. Однако учет вязкости жидкости видится важным, так как именно ею обусловлены демпфирующие свойства в данной колебательной системе и ограниченность амплитуд колебаний стенки канала на резонансной частоте. В работе [8] представлено исследование гидроупругих колебаний балки в потоке вязкой жидкости применительно к пьезопреобразователям, а в работе [9] проведено исследование плоского двухфазного течения вязкой жидкости в канале переменного сечения с твердыми стенками и учетом кавитационных эффектов.

С другой стороны, в работе [10] рассмотрен вопрос взаимодействия вибрирующих дисков со слоем вязкой несжимаемой жидкости, находящейся между ними, в том числе когда один из них представлен круглой упругой пластиной. Показано, что на резонансных частотах колебаний стенок канала амплитуда давления жидкости может изменяться на несколько порядков и становиться существенно меньше давления насыщенного пара. Аналогичное исследование в плоской постановке для пластин проведено в [11], а для круглых трехслойных пластин в [12]. Вибрация круглой пластины на свободной поверхности идеальной несжимаемой жидкости рассмотрена в [13]. При этом рассматривается область в жидкости, ограниченная жестким дном и цилиндрической поверхностью. Колебания круглой пластины, погруженной в воду со свободной поверхностью, исследованы в [14]. В работе [15] получено и исследовано интегродифференциальное уравнение для малых поперечных колебаний прямолинейного упругого трубопровода с идеальной несжимаемой жидкостью. При этом колебания трубопровода описываются в линейной постановке в балочном приближении.

В предлагаемой работе для исследования проблем возникновения вибрационной кавитации в жидкости приведено решение задачи о нестационарном движении пульсирующего слоя вязкой жидкости, взаимодействующей с упругой стенкой плоского канала, с учетом особенностей торцевого истечения.

Рассмотрим канал, условно представленный на рис. 1.

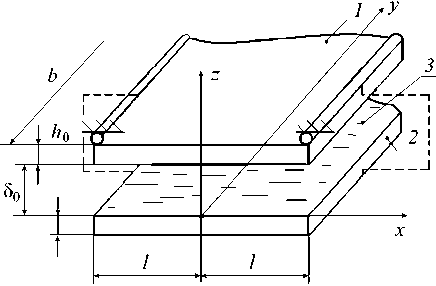
Рис. 1. Схема плоского канала с упругими стенками

Канал образован двумя параллельными непроницаемыми стенками 1 , 2 одинаковых геометрических размеров, между которыми движется пульсирующий слой вязкой несжимаемой жидкости за счет заданного закона изменения давления на торцах. Стенка 2 считается абсолютно жесткой, а стенка 1 представляет собой упругую пластину толщиной h ₀ с шарнирным опиранием на торцах. Геометрический размер канала 2 ℓ значительно меньше его размера b , а толщина слоя жидкости (расстояние между стенками) в невозмущенном состоянии δ₀ значительно меньше 2 ℓ . Вследствие пульсации давления возникают изгибные колебания стенки 1 , при этом амплитуда ее упругих перемещений значительно меньше δ₀ .

На торцах канала истечение в полости, заполненные той же жидкостью, можно считать струйным. Для определенности будем далее считать, что в левой полости давление постоянно, p ₀ , а в правой полости оно имеет постоянную составляющую и гармонически изменяющуюся по времени составляющую p ₀ + p ₁ ⁺ (ω t ) . Закон изменения давления на правом торце представим в виде

P + = p + m f p ^(to t ), fp (to t ) = exp( i to t ), (1) где p + m - амплитуда пульсаций давления на торцах канала; to - частота пульсаций; f _p (to t ) - закон изменения давления.

Введем в рассмотрение декартову систему координат x , y , z , связанную с абсолютно твердой стенкой 1 . Учитывая, что 2£ <<  b , будем считать канал неограниченным в направлении оси у , то есть перейдем к рассмотрению плоской задачи. В этом случае уравнения динамики вязкой несжимаемой жидкости в канале имеют вид

дV - дV    дV    1 дp Г d 2V d 2V ) —- + V —- + V —- = — -— + v x + д t      дx      дz    р дx ( dx2 dz2 J (2) д V Т7 д V д V 1 дp Г d 2V d 2V ) д V д V A —z. + Vx —z. + Vz —z. =---V + v —+ z , + z- = 0 d t      dx * dz     р dz ч дx2 dz2 v dx dz где p - давление; р, v - плотность и кинематический коэффициент вязкости жидкости; Vx , Vz - проекции скорости движения жидкости на оси координат.

Уравнения динамики жидкости дополняются граничными условиями:

условиями прилипания жидкости к стенкам канала [10, 11, 16]:

V x = 0, V z = 0 при z = 0; V_x = ^d u , V z = ^d w при z = S₀ + w     (3)

о t        о t и условиями ее свободного торцевого истечения, заключающимися в совпадении давления жидкости на торце канала с давлением в полости:

p = p о + p + (to t ) при x = £ ; p = p ₀ при x =- £ .           (4)

Здесь w - прогиб стенки 1 канала; u - продольное перемещение стенки 1 канала.

Для упругой пластины - стенки канала выполняется условие 2 1 << b , поэтому уравнения ее движения представляют собой уравнения динамики балки-полоски

⁵⁴ w , „ , д² w_

^D -,4 ⁺ Р0 h 0 3"Т = - q zz ’                         ⁽⁵⁾

dx        д t где qz = "Р + 2pv(dVz /дz) - нормальное напряжение, действующее со стороны жидкости на пластину; D = Eh03/(12(1 - ц0)) - цилиндрическая жесткость пластины; h0 – толщина пластины; ρ0 – плотность материала пластины; μ0 – коэффициент Пуассона материала пластины; Е – модуль Юнга материала пластины.

Граничные условия уравнений (5) – условия шарнирного опирания на торцах:

w = д ² w/ д x ² = 0 при x = ± £ .                   (6)

Введем в рассмотрение безразмерные переменные v = б 0/£ << 1, X = Wm /б 0 << 1, Re = б 0w/v, т = tot, - = x/ £, Z = z/ б о,

^V z = w m ^{to U} Z ; ^V x = w m ^{to U} -/ V ; Р = Р 0 ⁺ w m P^Vto(5 0 V 2 ) " 1 ^P ; ^W = w m^W , ⁽⁷⁾

u = u m U ; Р ⁺ = w m P^Vto(5 0 V ^{2 )} ' ^{P +} .

Здесь wm – амплитуда прогиба пластины; W – безразмерный прогиб пластины; um – амплитуда продольного перемещения пластины; U – безразмерное продольное перемещение пластины; ψ, λ, Re – парамет- ры, характеризующие задачу.

Подставляя введенные переменные (7) в задачу (1)–(6), получим задачу гидроупругости плоского канала в безразмерном виде, включающую уравнения динамики вязкой несжимаемой жидкости

Re

д U _z

д т

■ + X U; k

д U, 5 "д!

E д U, Y +U

. ^Z д Z JJ

д P 2 ^{д 2 U} - ^д 2 ^U 5 д - ^{+ V} l-²" ' ,д _ '

ψ2Re

д U,

д т

—+X U_;

д U,

—^Z+ U,

⁵ д ^

д U Z)"

^{Z д} Z J

д P, 2

^д Z ^{v v}

₂ д ² U _Z д ² U _Z "д !²"⁺" д ^^г

д U _z

+

д U _Z

= 0;

уравнения динамики упругой стенки канала

Dw_m д 4 W £ ⁴ д -⁴

⁺ P 0 h 0 to² w m

д ² W д т²

= Р 0 +

w_m ρνω δ 0 ψ²

P - 2 V²

д U _Z

J

Граничные условия (3), (4), (6) запишутся в виде

U _z = _v u^   , U _z = ^W при Z = 1 + X W ; U _z = 0, U _Z = 0 при Z = 0, (10)

w_m д т        д т

m p=p + (т) при z=1; p=0 при z = -1,             (11)

W = д 2 W /д Z 2 = 0 при z =± 1.                 (12)

В предлагаемой постановке ψ является безразмерным малым параметром, отношение um wm порядка единицы, следовательно, в нулевом приближении по ψ уравнения (8), (9) и граничные условия (10) упрощаются, то есть в них можно положить равными нулю члены порядка ψ и ψ2. Далее, рассматривая асимптотические разложения по малому параметру X<<1 [17] P=P0 +XP1 +...,Uz = UZ0 +XU^ +..,Uz = = Uz0 +XU?1 +... и ограничиваясь только первым членом разложения, получим линеаризованную задачу гидроупругости плоского канала, включающую в себя:

уравнения динамики слоя жидкости дU^0 дP0 д2U^0 дP0 _ дU^0 дUZ0

Re ^Г" ^-1C⁺^ZT ’ ^Z = ⁰ - : ⁺^Т " ⁰

с граничными условиями

Uz0 = 0, UZ0 =дW/дт при Z = 1; Uz0 = 0, UZ0=0 при Z = 0;(14)

p = p + (т) при z=1; P=0 при z=-1(15)

и уравнения движения пластинки – стенки канала

DWm д4W , , 2 д2W 14 д44 + Р°h°mw- дт2 = Р 0 + wm^ P        (16) δ0ψ2 с граничными условиями

W = д2W/дz2 = 0 при z=± 1.(17)

Решение уравнений (13) с учетом граничных условий (14), (15) и гармонического характера изменения по времени прогиба пластины – стенки канала имеет вид

U

= ¹ ξ 0 ⁼ 2 _ε 2

^{∂ P 0} + ^{∂ P 0} Ψ ( ζ ) + ^{∂ P 0} Φ ( ζ )

∂ξ∂τ ∂ξ∂τ ∂ξ

U ζ 0 = ₂ ¹ _{ε 2}

^∂ 2 ^{P 0}(1 -ζ ) + ^∂ 2 ^{P 0} Ψ 1 ( ζ ) + ^{∂ P} 2 ⁰ Φ 1 ( ζ )

∂ξ ∂τ       ∂ξ ∂τ ∂ξ

∂W +, ∂τ

n f 2 d ²W д W, 1 _nf / ₂ d ²W d W

P 0 = J J ^{28 a} + 12Y^ d^d Z dZ + 1) II 2^{8 a + 12}Y^ d ^ d ^ ⁺

- 1 ^       д т         д т у 2        - 1 ^      д т          д т

+ P ₁ ⁺ 2 + ξ P ₁ ⁺ 2.

Здесь введены обозначения

ε ( ω ) = Re2, F 1 ( εζ ) = ch εζ cos εζ , F 3 ( εζ ) = 1 2sh εζ sin εζ ,

F 2 ( εζ ) = 2 [ ch εζ sin εζ+ sh εζ cos εζ ] , F 4 ( εζ ) = 4 [ ch εζ sin εζ- sh εζ cos εζ ] ,

D ₌ sh ε- sin ε D ₌ sin ε+ sh ε

1 cos ε+ ch ε ,    2 cos ε+ ch ε ,

γ ( ω ) =

1                  ε 3 (sh ε- sin ε )

6 ε 2 (ch ε+ cos ε ) - 2 ε (sh ε+ sin ε ) + 2(ch ε- cos ε )

_α ( _ω ) ₌         ε ( ε (ch ε+ cos ε ) - (sh ε+ sin ε ))

ε 2 (ch ε+ cos ε ) - 2 ε (sh ε+ sin ε ) + 2(ch ε- cos ε )

Ψ ( ζ ) = F 2 ( εζ ) D 1 - F 1 ( εζ ) - 2 F 4 ( εζ ) D 2 ,

Ф ( Z ) = 2 F 3 ( £Z ) - F 2 ( eZ ) D 2 - 2 F 4 ( eZ ) D i , ^ i ( Z ) = J ^ ( Z ) d Z ,

ζ

ФI(Z)=I $(Z)d z.

ζ

Решение уравнений (16) с учетом краевых условий (17) представим в виде ∞ w = E(Rk(т) + R°k )cos((2k - 1M)/2 + Qk(i)smkn^ .       (19)

k = 1

Верхний индекс 0 в (19) означает решение, соответствующее постоянному уровню давления р 0 , не зависящему от τ.

Принимая во внимание линейность уравнения (16) и подставляя в него (19), найденное выражение для давления (18), а также раскладывая оставшиеся члены, входящие в его правую часть в ряды по триго- нометрическим функциям, получим уравнение для составляющей, не зависящей от времени Rk0 :

^

2 k - 1 ) 4 п         2 к — 1 t V 4( — 1) k + ¹        2 ^к — 1 t

-----п DwR_kcos-----пс = 2 --------Ро cos----- пс, (20)

21 J m k 2 s £(2к-1)п        2 S и уравнение для неизвестных функций времени Rk и Qk :

^

E Wm D k=1

2 k - 1 I4_D 2 k - 1 , кkп I" . , , ----п R, cos---- пс + D — Q, sin kпс +

21 J k 2 V 1 J

^{+ p} о h о ^{ю 2}

(d-R*

V d т²

2 k -1 _t . d 2 Q_k • cos----- пс +--7^ sin kпс

2 ^S    d т²         J

=E

k = 1

4( - 1) k ^{+ 1} p + (2 k - 1)п 2

2 k -1 cos—2— пс, +

2( - 1) k ^{+ 1} Р 1 ⁺

sin kπξ

-

^

Г

-

' w m E ^M ck ®

k = 1

V

2d2Rk+1K mRR*I 1 -tt+2 Kck °, dт           dт J

2 k - 1 _e cos πξ

-

2d2Qk+?K ddQ^ I 1 "TT + 2 Ksk ° ,

^- M sk ® V

sin k п^ .

d т            d T j

Учитывая, что d ² R _k I d т² = - R _k , d ² Q _k j d т² = - Q _k , вводя обозначения

ρν

^M ck e 2

δ0ψ2

• ²    ] 2 2£ 2 а. ₂ K = ¹² y® M . M = p^v Г ¹ 1 ²^!а.

(2 k - 1)п J to ’ ^ck 28² a ^ck’ ^sk 5 0 v² L * п J ® ’

2Ksk = ^^Msk-     ax ,=((2k-1)я/2t)4-[p0h0 + McJm2D ;     a2c,= sksk1сk00ck2сk 2ε2α

= 2Kckо/D; a1sk =(kл/1)4 -[p,h0 + Ms*]m2/D; a2,k = 2K„.m/D и приравнивая коэффициенты при косинусах и синусах, из (20) находим выражение для Rk0 :

R k = ( 21/ ((2 k - 1)п) ) 4 ( 4( - 1) ^{k + 1}/ ((2 k - 1)п) ) p „ ( Dw m ) ¹,       (22)

а из (21) – уравнения для определения R_k (τ) и Q_k (τ):

" 1,k W m R k + a 2 .k W . dR kl d т = 2( - 1) ^{k + 1}/ ((2 k - Г^пD ) p m, f„ (т),     (23)

• a, w-.Q. + a 2 *w . dtid т = ( - 1) k ^{+ i}/ ( knD ) p*..f, (t).        (24)

Частные решения уравнений (23), (24), соответствующие гармоническому закону пульсаций давления на торце канала (1), имеют вид

_ 2( - i) ^{k + 1} p m

-Rl- -- k (2k -1)n wmD

( - i) k + i	р + pm
k π	w D m

л df^+в f ck dт + ckfp ’ df 1

A s/г + B sk f p , d т

aa a где Ack        2,2’ Bck 2,2’ Ask        2,2’ B ai ck + a 2 ck          ai ck + a 2 ck            ai sk + a 2 sk

a i sk

'sk „2 , „2 a i sk ⁺ a 2 sk

.

С учетом (25) прогиб стенки 1 имеет вид га w - wm E k -i

2( - i) ^{k +i} __________ (2 k - i)n И (2 k - i)n J

4 о          +

² p 0 + p m

Dwm Dwm

df

A ck²^ + ^Bck f p d τ

2 k -1      (-i)k+i p+ xcos----n£+2 <--mS-

2        k n w„D

m

df p       i

Ак” + B_Skfp sin k nu - sk sk p

d τ

- p о у d E

га

4( - i) ^{k + 1} (

2£

(2 k - 1)п ( (2 k - 1)п )

2 k - i _e cos----л£ +

⁺ p m А ⁽^’®^)exp[ i ⁽t + ф⁽^ го»].

где А (^,ю) - 4C (^,to) ² + B (^,ю) ² ; ф(^,ю) - arctg ( C (ЗД/ B (^m) ) ,

^

C (E’to) - E

2( - i) ^{k + i} A_ck    2 k - i

—— --c ^ cos----

(2 k - i)n D

пе +^ HT A sk k - i   k п    D

sin k лЕ, ,

в (E’to) -t ^-^ B c^ _ k - i (2 k - i)n D

2 k - i

: os-------

^

( - i) ^{k +} ' Bs_L k π   D

Используя найденное выражение для прогиба (26), окончательно определяем закон изменения динамического давления в безразмерном виде:

Г df

x 12y B.    - Ackfp ck ck p

-

d τ

p m

Dw m

га

z

« = ? V (2 k - 1)n J

Г     df„

28²a A_k -^р + B_ckf„ ck ck p

d τ

cos

k + 1

A

k + i               df

■Z . I (-1)    1'y B '-Askfp dτ

га

k + 1

-

k = 1

π k

Г dfn

28²a A_S k^- + BJ_p

V    d ^T

sin k πξ

J

и в размерном виде:

P = P i ⁺ (t)(1 + 5 )/2 + p m П(5, to)sin(T + ф p (5, to)),           (28)

ρνω ₂₂ 12          S (ξ,ω)

где П(5,to) = ——^( 5 (5,to) + Q (5,to) ) , ф^(5,ю) = arctg———,

D δψ²                                 Q (ξ,ω)

га

5 (5, to)=E k=1V (2 k -1)n J

³ k + ¹                                Г 2 k - 1 1

(-1) (12yBck - 28 aAQt) cos I       n5 J +

1A            k + 1

k + 1

+El "Г I (-1) (12YBsk - 28 aAsk )Sin kn5 , k=1V П k J га

Q (5,to)=E k=1

Г 2 ^л

V (2 k - 1)n j

‘/                            Г 2 k - 1     1

(-1) (12yAc, + 28 oBck)cosI       n5 J + га Г 1 I3 +El — I k=1 V nk J

k

( ^{- 1} ) ( ¹²y A sk ⁺ 2 ^8aBsk ) sin ^{k n5}.

Первое слагаемое в выражении прогиба (26) представляет собой прогиб под действием статического давления, а второе слагаемое – прогиб, обусловленный динамическим давлением в канале. В выражении для динамического давления (28) слагаемое p 1 (т)(1 + 5)/2 отражает линейное падение давления вдоль канала, а второе слагаемое представляет собой давление в жидкости, обусловленное ее сдавливанием упругой стенкой канала. При этом хорошо видно, что первое слагаемое динамического давления вдоль канала не превосходит заданного давления на торце p 1 (т) .

Заметим, что в выражениях (26), (28) получены функции А (ξ,ω) , Π(ξ,ω) , которые можно рассматривать как частотозависимые функции распределения относительных амплитуд прогиба и динамического давления вдоль канала. Аналогично функции φ(ξ,ω) , φ _p (ξ,ω) можно рассматривать как частотозависимые функции распределения фазового сдвига прогиба стенки и давления в канале относительно исходного возмущения на торце. В случае фиксированного значения продольной координаты ξ указанные функции представляют собой амплитудные частотные характеристики и фазовые частотные характеристики прогиба стенки и давления в заданном сечении канала. Таким образом, на базе расчетов функций А (ξ,ω) , φ(ξ,ω) можно исследовать упругие колебания пластины – стенки канала, возбуждаемые пульсацией давления на торце (1) с амплитудой р _m ⁺ и частотой ω, а при помощи функций Π(ξ,ω) , φ _p (ξ,ω) исследовать изменение давления вдоль канала, вызванное сдавливанием жидкости упругой пластиной – стенкой канала при ее изгибных колебаниях.

В качестве примера рассмотрим исследование упругих прогибов пластины – стенки канала и динамического давления, обусловленного сдавливанием жидкости упругой стенкой, в центре (ξ = 0) канала с параметрами: ℓ = 0,1 м; δ 0 / ℓ = 1/15; b / ℓ = 5; ρ = 1,84∙10³ кг/м³; ν = 2,5∙10^–4 м²/с; р _m ⁺ =1Па, ρ 0 = 7,87∙10³ кг/м³; h 0 = 3,2 мм; Е = 1,96∙10¹¹ Па; μ 0 = 0,3.

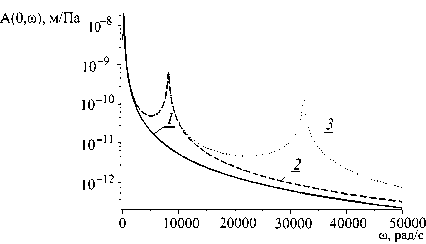
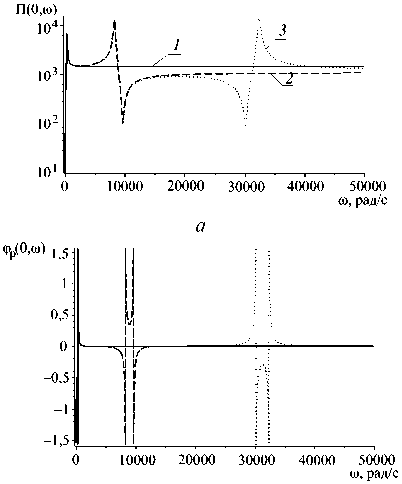
Результаты расчетов относительных амплитуд прогибов стенки канала А (0,ω) и фазового сдвига φ(0,ω) в зависимости от частоты возмущения на торце при удержании одного, двух, трех членов ряда приведены на рис. 2 (кривая 1 – в расчетах удержан один член ряда; кривая 2 – в расчетах удержаны два члена ряда; кривая 3 – в расчетах удержаны три члена ряда). Аналогичные результаты расчетов для относительного давления Π(0,ω) и фазового сдвига φ _p (0,ω) приведены на рис. 3.

а

co, рад/с

б

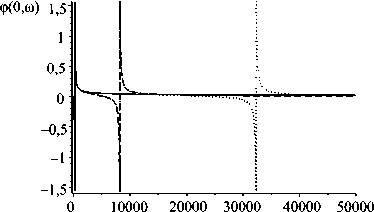
Рис. 2. Результаты расчетов относительных амплитуд прогибов А (0,ω) пластины ( а ) и фазового сдвига φ(0,ω) ( б ) в зависимости частоты возмущения

б

Рис. 3. Результаты расчетов относительных амплитуд давления П(0,ω) жидкости ( а ) и фазового сдвига φ _р (0,ω) ( б ) в зависимости частоты возмущения

Проведенное исследование показывает, что наблюдаются пики амплитуд прогибов пластины на резонансных частотах колебаний, данным частотам соответствуют пики давления в жидкости . При этом давление, обусловленное сдавливанием жидкости упругой стенкой, на резонансных частотах превышает заданное давление на торце на 3–4 порядка. Резонансным частотам соответствует смена фазового сдвига с –π/2 на π/2, на остальных частотах он стремится к нулю. Учет второго и последующих членов ряда в выражении (26) приводит к появлению дополнительных пиков прогибов, а следовательно, и давления, которые соответствуют новым резонансным частотам, расположенным в более высоком частотном диапазоне, чем предыдущие резонансные частоты. Для практических целей достаточно удерживать первые 3–4 члена ряда, так как частоты колебаний стенок канала и пульсации давления на практике не превышают звуковой диапазон. Принимая во внимание гармонический характер изменения давления по времени, можно говорить о расчетах, показывающих, что на резонансных частотах давление может становиться меньше давления насыщенного пара. Таким образом, даже незначительная пульсация давления на торце вызывает значительные изменения давления в канале, обусловленные сдавливанием жидкости упругой стенкой канала на резонансных частотах колебания, что приводит к возникновению вибрационной кавитации в жидкости. Следовательно, гидроупругие колебания стенки канала являются основной причиной резкого роста динамического давления в жидкости на резонансных частотах колебаний. Полученные в работе выражения для прогиба упругой стенки канала и гидродинамических параметров слоя вязкой жидкости могут быть использованы в практике для определения резонансных частот колебаний, соответствующих условиям возникновения кавитации, а также для оценки возможности возникновения резонансных колебаний исходя из заданного частотного диапазона возможных пульсаций давления на торце канала.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (проект № 32).