Математическая модель движения судов с нестандартным движительно-рулевым комплексом

Стандарт IEC (International Electro-technical Commission) 62065 отражает эксплуатационные требования, методы тестирования и результаты испытаний, требуемые для следящих систем и систем автоматического управления, используемых в морской навигации.

Настройка модели по стандарту IEC 62065 осуществляется за счет сравнения графиков циркуляции: первого – получен при моделировании с графиком и второго – получен при ходовых испытаниях ¹ . Общий вид модели представлен на рис. 1.

Рис. 1. Блок-схема ММДС по стандарту IEC 62065

Fig. 1. Flowchart of the mathematical model of the moving ship according to IEC 62065

В результате анализа данной модели выявлены как ее неоспоримые плюсы, так и недостатки. К достоинствам можно отнести следующие качества:

• 1)    все значения, используемые в ММДС, можно получить на практике или из графиков ходовых испытаний;

• 2)    при расчете скоростей нет необходимости моделировать гидродинамику судна.

Недостатки модели:

• 1)    изначально предназначена для судна со стандартной комплектацией ДРК;

• 2)    не учитывает влияние ветра;

• 3)    движение судна моделируется плоско-параллельным.

Данный метод значительно упрощает моделирование движения судна при разработке алгоритмов управления различных систем автоматического управления. Кроме того, появляется возможность не производить расчет гидродинамики модели судна, как предусматривалось прежними методами [1–5]. Это позволяет избежать погрешностей, связанных с неадекватностью модели. Большая часть литературы, посвященной данной тематике, писалась в 1960–80-х гг., поэтому в расчетах используются теоретические графики обводов корпусов судов, опытные значения коэффициентов гидродинамики и аэродинамики, различные номограммы для конструкций судов и их ДРК, которые использовались в тот период времени. В настоящее же время разработано множество новых конструкций корпусов судна и новых ДРК, принципы работы которых значительно отличаются от прежних. Оценка маневренных характеристик моделируемого судна по стандарту IEC 62065 производится с помощью графика установившейся циркуляции судна, который рекомендован для данной цели сертификационными сообществами ² и учебной литературой [6].

Одним из самых весомых недостатков модели по стандарту IEC 62065 является то, что она предназначена для судов со стандартным ДРК. Данная модель рекомендована стандартом для испытания систем автоматического управления курса судна (САУКС). Однако проанализировав работу систем динамического позиционирования (СДП) ³ и описание математических моделей [4; 7], используемых в них, авторы пришли к выводу, что для испытания данных систем она не пригодна. Целью исследования является исправление этого недостатка, а также введение параметра внешнего (ветрового) воздействия в модель по стандарту IEC 62065.

Материалы и методы

За основу математической модели движения судов с нестандартным движительно-рулевым комплексом, рассматриваемую в настоящей работе, принята математическая модель движения судна по стандарту IEC 62065.

Обработка модели

В качестве модельного объекта исследования было принято судно снабжения "Витус Беринг", имеющее в ДРК две винто-рулевые колонки (ВРК) по типу "азипод" и носовое подруливающее устройство. Параметры судна, используемые в расчетах, приведены в табл. 1.

Таблица 1. Характеристики судна, используемые в расчетах Table 1. Ship's characteristics used in the calculation

u max , уз	v max , уз	l a , м	l b , м	b , м	P 1,2 , кВт	P 3 , кВт	T p , с	R δ1 , 1 °/с	R δ2 , 1 °/с
16,75	4	42	26	4,7	6500	2600	8	4,5	9

Примечание. R _δ1 – скорость разворота азипода при работе с одним гидравлическим приводом; R _δ2 – скорость разворота азипода при работе с двумя гидравлическими приводами.

В конечном виде блок-схема ММДС, приведенная на рис. 2, описывается следующим образом: 1 – левый азипод; 2 – правый азипод; 3 – носовое подруливающее устройство; d – значение уставки; a – текущее значение; g – относительно земли; w – относительно воды; обозначения: P – значение мощности, потребляемое элементом управления; δ – значение угла перекладки азипода; u – скорость продольного движения; v – скорость поперечного движения; r – угловая скорость; X' – нормированное значение тяги, обеспечиваемое ДРК; K – скоростной коэффициент; M' – нормированное значение момента, обеспечиваемое ДРК; γ – коэффициент стабильности (отношение расстояния центра давления боковых сил к длине судна); W' – нормированное значение момента, создаваемое волнением; T – значение компоненты скорости влияния глубинного течения и ветрового воздействия; τ – временная константа; Hdg – значение курса судна; ^, E – значения координат судна относительно севера и востока.

В отличие от параметров блок-схемы, представленной на рис. 1, в блок-схему на рис. 2 дополнительно введены две модели управления тягой и вместо одной модели управления рулевым устройством установлено две. Все эти преобразования необходимы для моделирования работы ДРК выбранного судна.

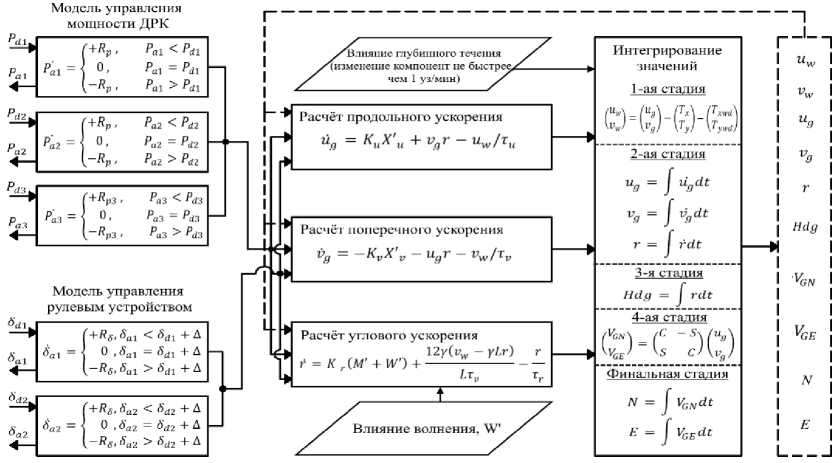
Рис. 2. Блок-схема измененной ММДС

Fig. 2. Flowchart of the changed mathematical model of the moving ship

Во многом принцип расчетов в самих моделях остался прежним, но изменился подход нормирования величин. Сделано это по ряду причин. На рис. 3 представлено схематичное изображение судна, элементов управления, а также создаваемых ими сил и моментов: индексы: 1 – левый азипод; 2 – правый азипод; 3 – носовое подруливающее устройство (НПУ); a – текущее значение; u – продольное направление движения; v – поперечное направление движения; обозначения: P – значение мощности, прилагаемое элементом управления; δ – значение угла перекладки азипода; ЦТ – центр тяжести; ДП – диаметральная плоскость; l a – расстояние НПУ от центра тяжести; l b – продольное расстояние ВРК от центра тяжести; b – поперечное расстояние ВРК от центра тяжести; M – момент, создаваемый i -м элементом управления.

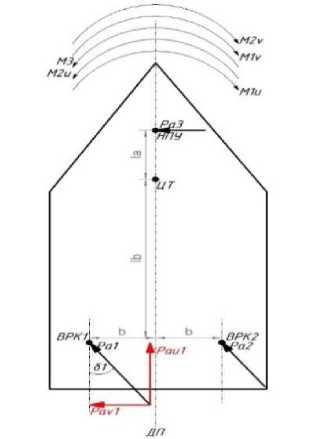
Рис. 3. Схематичное изображение судна Fig. 3. Schematic image of the vessel

На рисунке видно, что при развороте ВРК для расчетов прилагаемой тяги по осям необходимо находить проекции этих сил относительно угла разворота ВРК. В связи с этим необходимо отказаться от работы с нормированными значениями угла разворота в пользу натуральных величин для удобства расчетов. Также был изменен принцип получения нормированных значений тяги из-за особенностей ДРК. Получение нормированного значения тяги, как в стандарте IEC 62065, приведено в формуле (1)

Р X

-2- = —= X ‘,                                  (1)

PX max max где Pa – текущая мощность, передаваемая на винт; Xa – текущая тяга, создаваемая винтом; X' – нормированное значение тяги.

Как видно из формулы (1), значение X' получается делением текущего значения мощности на максимальное. Так как принцип работы ДРК выбранного судна отличается от того, что приведен в стандарте, необходимо при расчете учитывать максимальные мощности в зависимости от направления их воздействия для движения судна.

Результаты и обсуждение

Продольное движение

Расчет тяги для продольного движения представлен в формуле (2). Стоит отметить, что максимальная тяга будет создаваться при угле разворота ВРК в 0°. Для получения значения нормированной тяги необходимо разделить сумму проекций на ДП текущих мощностей на максимальную, создаваемой ВРК.

р =Р+Р ^J max u ^J 1 ^{+ J} 2 ,

P aui = P ai COS S ai ,                                                       (2)

• _x‘= Z 2 = 1 P aui = Z 2 = 1 P ai COS S ai u ^,

maxu               max u где Pmax u - максимальная мощность для продольного движения; XU - нормированное значение тяги продольного движения; Paui – текущее значение мощности продольного движения (проекция на ДП).

Расчет продольного ускорения остался прежним и представлен в формуле (3)

u g = K U ^X U + v g r - u w / ^T u .                                           ⁽³⁾

Вращательное движение

Отдельного внимания заслуживает преобразование расчета вращательного движения. Изначально в стандарте используется нормированное значение момента, создаваемого рулем в струе винта с максимальным значением при перекладке в 35°. Данный способ не подходит для ДРК с активными элементами управления, но при использовании принципа получения нормированных значений тяги, приведенных выше, а также знаний теоретической механики, схемы судна и расположения ДРК на рис. 3, можно получить нормированный вращательный момент.

Пусть ЦТ является центром вращения, находится в ДП и расчет создаваемых моментов ведется относительно него. Кроме того, необходимо определить условие максимального вращательного момента. Для данного судна в документации по его эксплуатации ⁴ предусмотрена максимальная скорость разворота, представленная в табл. 2.

Таблица 2. Маневренные характеристики моделируемого судна

Table 2. Maneuvering characteristics of the modeling ship

Элемент управления	Мощность	Скорость поворота при нулевой скорости хода
НПУ	2 200 кВт	1,7 °/с
НПУ + азипод 90°	2 200 + 6 500 кВт	4,8 °/с

При создании бόльшего вращающего момента развивается большой крен, что негативно сказывается на эксплуатации судна в целом. Следовательно, условие максимального момента будет создаваться при условии, приведенном в формуле (4)

M max = ( P 1 + P 2 ) L b + P 3 / a ,

при P1 + P2 = 6 500 кВт и P3 = 2 200 кВт, где Mmax – максимальный вращательный момент, создаваемый ДРК; la – расстояние носового ПУ от ЦТ; lb – расстояние азиподов от ЦТ.

Расстояния элементов управления от ЦТ являются рычагами вращения, создающими пропорциональность воздействия элемента ДРК. Также учитывается момент, создаваемый ВРК из-за расстояния от ДП. Так как используется правая координатная система, то поворот влево выполняется со знаком минус, следовательно, данный момент у левого ВРК будет положительным, а у правого – отрицательным. В случае когда тяга и направления обоих ВРК равны, данные моменты взаимокомпенсируются. Также необходимо учитывать угол разворота элемента ДРК, чтобы рассчитать проекцию сил, воздействующих на рычаги. Расчет текущего вращательного значения и его нормированного значения приведен в формуле (5)

i = 1 ai            i = 1 ai ai b a1          a1 a2          a2           a3 a , m ' =

∑ i³ = 1 ^M ai

^M max

где M _max – максимальный вращательный момент, создаваемый ДРК; M _ai – текущий момент, создаваемый i -м элементом управления; M' – нормированное значение момента, создаваемое ДРК; b – расстояние азипода от ДП.

Способ расчета углового ускорения представлен формулой (6)

Г- = K r ( M ' + w ‘ ) +

12Y ( vw -YL^r ) r _ _ _

.

L ^T v         ^T r

Поперечное движение

Расчет поперечного движения также был нами изменен. Факторы элементов управления выбранного ДРК, которые могут вызывать поперечное воздействие на движение судна, учитываются в расчетах модели.

Для получения нормированного значения тяги в поперечном движении следует определиться с понятием максимальной поперечной тяги.

В концепции данной модели в поперечном движении максимальной тягой принято считать значение тяги при движении судна лагом с максимальной скоростью. Для получения такого движения судном необходимо выполнить следующее условие:

∑ ³ M

M' = =^1=

^M max

Из этого условия следует, что нормированное значение тяги для движения судна лагом с максимальной поперечной скоростью будет рассчитываться:

PL = f У Psin90° IL, 3 a               aib

V i = i

P = P3la ai

f ?pj

2 P ₃ l _a

^Pmax v    I ^P 3 ⁺ r^. I   ^P 3 ( 1 ^{+ b} ) ,

V где ε – отношение расстояния НПУ до ЦТ к расстоянию ВРК до ЦТ; Pmax v – максимальная мощность для поперечного движения.

Получение нормированного значения поперечной тяги осложнено особенностью конструкции. Так как элементы ДРК находятся на расстоянии от ЦТ, то при отсутствии компенсации вращательных моментов силы, формируемые азиподами и НПУ, будут создавать вращение, а не поперечное смещение ЦТ. Чтобы решить эту проблему, необходимо связать расчет поперечной тяги с расчетом вращательного момента. Это решение представлено в формуле (9)

X v =

Z ² = 1 P» sin ⁵ a- ^{+ P} a 3

P max v

k p

P

2 m

P max v

где X V, - нормированное значение тяги поперечного движения; P ai - текущее значение мощности; P ^ _м

–

суммарная мощность ДРК при развороте на месте с максимальной угловой скоростью; k p – коэффициент пропорциональности мощностей.

Смысл данной формулы состоит в следующем: при создании условия для поперечного движения часть уравнения k p M' равняется нулю, соответственно, вся прилагаемая мощность воздействует на ЦТ и перемещает его в поперечном направлении. При создании условий для поворота на месте вычитаемые части уравнения сравниваются и в результате дают ноль, означающий отсутствие воздействия сил для поперечного смещения ЦТ. Коэффициент пропорциональности мощностей необходим для выравнивания значений суммарной относительной тяги и значения относительного момента при условии разворота на месте. Если суммарное значение мощностей для разворота на месте с наибольшей угловой скоростью совпадает с мощностью, используемой для движения лагом с максимальной скоростью, то коэффициент будет равен единице.

Чтобы из нормированного коэффициента тяги получить значение компоненты ускорения, создаваемой элементами управления, вводится коэффициент тяги К„. В результате конечная формула расчета поперечного ускорения имеет вид vg =- К Xv-Ug r - Vw / Tv. (10)

Определение коэффициентов и констант

Расчеты скоростных коэффициентов изменились после ввода новых воздействий ДРК на судно для данной модели и изменения расчета угловой скорости. Способ расчета коэффициентов для новой модели представлен формулами (11)

^K u ^U max / ^T u , ^K v = ^V max / ^T v , ^K r = ^R max / ^T r ,

где u max – максимальная продольная скорость, равная максимальной скорости движения судна вперед (табл. 1); v max – максимальная поперечная скорость, равная максимальной скорости движения судна лагом под 90° (табл. 1); r _max – максимальная угловая скорость, равная максимальной скорости разворота судна на месте (табл. 2).

Максимальные скорости определяются с учетом результатов ходовых испытаний или из данных судовой документации. Для определения этих скоростей необходимо выполнить условия для создания максимальной нормированной тяги или момента (движение прямо при максимальной тяге винтов; движение лагом под углом в 90°с максимальной тягой; разворот на месте с максимальной тягой).

Значения временных констант ускорений т „ , T _v , т _г отражают плавность набора той или иной скорости. Следовательно, один из способов их определения – анализ существующих графиков скоростей отдельных видов движения (ускорение судна при движении вперед, ускорение судна при движении лагом, ускорение угловой скорости при развороте на месте) либо опытное построение таковых с подбором параметров констант до совпадения опытных значений с моделируемыми. Также возможен вариант поиска параметров подбором значений по графику маневра циркуляции.

При моделировании движения судна значение коэффициента стабильности γ выбрано равным нулю, так как для упрощения расчетов было введено условие, что центр вращения судна совпадает с центром тяжести. Для более точного моделирования необходимо тщательное наблюдение за реальным объектом, чтобы создать функцию, описывающую зависимость коэффициента γ от скорости и типа движения судна.

Введение ветрового воздействия

Отсутствие ветрового воздействия при моделировании можно компенсировать суммированием компоненты скорости течения с компонентой скорости ветра, умноженным на коэффициент обтекаемости корпуса. Данный коэффициент можно получить опытным путем, анализируя снос судна при определенной скорости ветра

T wd = ^U wd cos ( Y wd ) ,

T Swd = ^U wd ^Sin ( Y wd ) ,

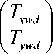
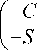
S T   K   ]

Г Пт   К  I’

^C 7 XT Ewd K wdv )

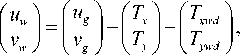
где uw и vw - продольная и поперечная составляющие скорости судна относительно сил, действующих на судно; С и S — косинус и синус текущего курса судна; TN и TE — компоненты! скорости глубинного течения в северном и восточном направлении; TY и TX — компоненты скорости глубинного течения в координатной системе, привязанной к судну; Uwd - скорость ветра; TNwd и TEwd - компоненты скорости ветра в северном и восточном направлении; TYwd и TXwd - компоненты скорости влияния ветра на судно; Kwdu и Kwdv -коэффициенты пропорциональности ветрового воздействия для продольного и поперечного движения соответственно.

Моделирование движения

Используя данную методику расчета и данные судна "Витус Беринг", указанные в табл. 1 и 2, были получены графики движения судна, приведенные на рис. 4.

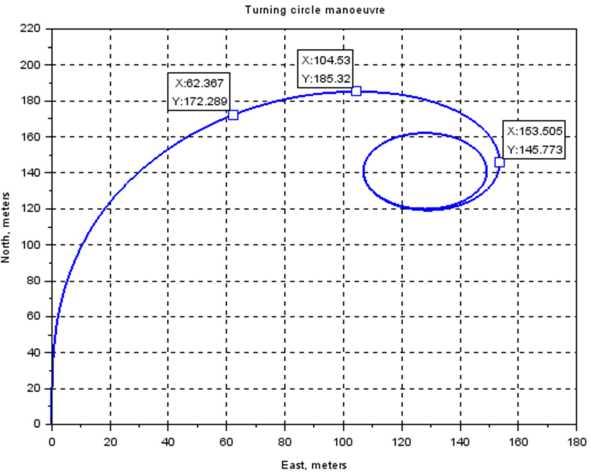
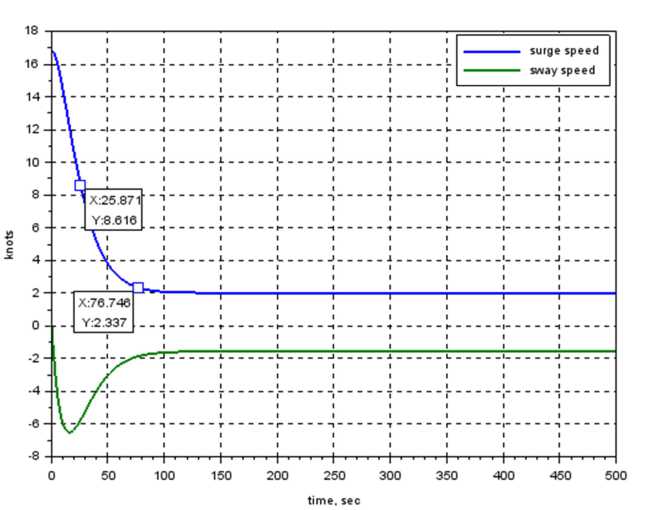
Рис. 4. Графики установившейся циркуляции и скоростей движения судна

Fig. 4. Diagram of turning circle maneuver and velocities of the ship

Адекватность полученной модели можно оценить сравнением полученных значений и значений графика циркуляции из документации, прилагаемой к судну (рис. 5), а именно: развиваемые судном расстояния во время маневра, параметры значений скорости в контрольных точках (при развороте судна на 90 и 270 градусов), время, за которое эти точки были достигнуты. Значения коэффициентов, временных констант и относительных погрешностей, полученных при моделировании, приведены в табл. 3.

Таблица 3. Параметры настройки модели и ее выходные значения Table 3. Model's adjusting parameters and output values

Погрешность	τ u , с	τ v , с	τ r , с	γ , о.е.	∆ S , %	∆ U , %	∆ T , %
	121	7,8	0,17	0	20,4	6,91	6,59
	Диаметр, м	Выдвиг, м		Смещение, м
	154	185		62,3
δ, %	10,8	26,5		24
	u 90 , уз	u270 , уз	t90 , с	t270 , с	А ^ , %
	8,61	2,34	25,9	76,7	11,3
δ, %	12,2	1,65	3,6	9,57

Примечание. u 90 , u 270 – значения параметров продольной скорости в момент разворота судна на 90 и 270°; t 90 , t 270 – время, затраченное судном для разворота на 90 и 270°; δ – относительная погрешность по выбранному параметру; ∆ S , ∆ U , ∆ T – среднестатистическая погрешность по расстоянию, скорости, времени соответственно; ∆ ∑ – среднестатистическая погрешность по всем параметрам.

Для удобства сравнения значений с испытаний и снятых с математической модели на графике (рис. 5) обозначены маркеры со значениями в контрольных точках. Моделирование проводилось в текстовом редакторе SciNotes программного пакета SciLab 6.0.0.

РАСЧЕТНАЯ ЗАГРУЗКА; ОСАДКА КОРМОЙ 7.50 м, ОСАДКА НОСОМ 7.50 м

НА ПОЛНОЙ СКОРОСТИ ВПЕРЕД, управление штурвалом; угол Азипод - 35°

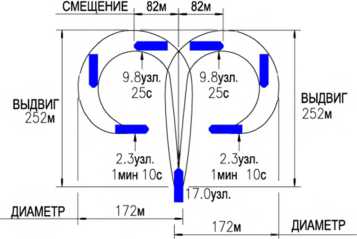
Рис. 5. График циркуляции судна "Витус Беринг" (согласно документации)

Fig. 5. Diagram of turning circle maneuver of the ship "Vitus Bering" (according to the documentation)

Выводы

В результате анализа модели, предлагаемой стандартом IEC 62065 для тестирования систем автоматического управления, выявлены как недостатки, так и бесспорные преимущества представленного метода моделирования. Основным недостатком метода являются расчетные формулы для стандартного типа ДРК. Этот недостаток был устранен поправками в методе расчета, приведенными в данной статье. Кроме того, для примера работы модели смоделировано движение типового судна "Витус Беринг". Полученные погрешности свидетельствуют об упрощенности модели, вследствие чего не учитываются некоторые параметры, такие как влияние крена и дифферента, развиваемые во время движения, изменение положения центра вращения. Линейность модели также может сказываться на наличии погрешностей. Не стоит исключать того, что испытательные характеристики маневра циркуляции были зафиксированы не в идеальных условиях. В любом случае средняя статистическая погрешность для упрощенной модели в 11 % более чем удовлетворительна для предварительной разработки и испытаний алгоритмов управления САУ.

Используя подобную методику, можно преобразовать модель для плавательного объекта любой формы и типа ДРК. Главным преимуществом представленной модели является отсутствие необходимости расчетов гидродинамических свойств. Это придает особую ценность данной методики для разработчиков алгоритмов, так как с ее помощью возможно быстро и легко смоделировать движение судна, не заостряя внимания на расчетах гидро- и аэродинамических коэффициентов.