Математическая модель двухкомпонентной фильтрации применительно к механическому обезвоживанию осадков

Для многих отраслей промышленности задача повышения эффективности обезвоживания сжимаемых осадков имеет большую практическую значимость. Так, например, при производстве бумаги себестоимость и качество выпускаемой продукции напрямую связано с эффективность обезвоживания бумажного полотна в прессовой части. Также решение проблемы экологической безопасности невозможно без решения проблемы утилизации отходов сточных вод предприятий, относящихся к различным отраслям промышленности. Для решения этих задач широко используются различные методы механического обезвоживания осадков. В данной работе предложена математическая модель процесса механического обезвоживания сжимаемого осадка на примере прессования влажного бумажного полотна в прессовом захвате бумагоделательной машины, образованном двумя прессовыми валами.

Прессовый захват характеризуется шириной площадки контакта валов а и законом распределения внешнего давления q(х) по ширине площадки контакта (рис.1).

Выжимаемая из бумажного полотна вода удаляется в прессовое сукно, играющее роль фильтровальной перегородки и имеющей незначительное по сравнению с бумажным полотном гидравлическое сопротивление. Часто прессование происходит между двух сукон, что позволяет значительно повысить эффективность обезвоживания в результате сокращения пути фильтрации удаляемой воды.

Полагаем, что вода, выжимаемая из осадка, движется в направлении, перпендикулярном движению осадка, а ширина площадки контакта а на порядок меньше радиусов валков и на порядок больше толщины сжимаемого осадка h . В связи с этим при выводе уравнения, описывающего процесс обезвоживания осадка в прессовом захвате, можно рассматривать уплотнение элемента осадка единичной площади, лежащего на водопроницаемом основании и нагружаемого внешней нагрузкой, изменяющейся по закону q(t) , где t = x / v , где v – скорость движения фильтрующей ткани.

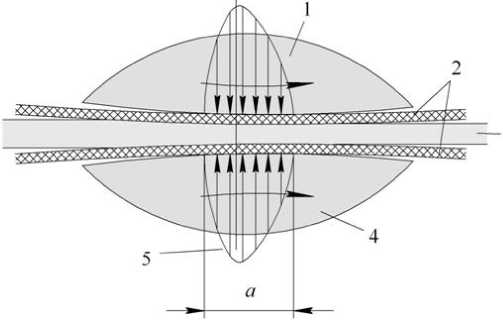
Рисунок1 – Схема прессового захвата: 1 – верхний вал; 2 – фильтровальная ткань (прессовое сукно); 3 – обезвоживаемый осадок; 4 – нижний вал; 5 – эпюра внешнего давления

Сжимаемый осадок будем рассматривать как пористую среду, состоящую из твердых частиц, связанных между собой и образующих «скелет» осадка, воды и воздуха, находящихся в порах осадка. При отсутствии воды и воздуха уплотнению осадка под действием внешней нагрузки препятствовало бы только сопротивление сжатию «скелета». В действительности на «скелет» действует только часть внешней нагрузки. Другая ее часть воспринимается находящимися в порах водой и воздухом. В результате в поровой воде и воздухе создается избыточное гидростатическое давление. Будем считать давление воздуха в порах осадка и давление воды одинаковыми, т.е. будем пренебрегать капиллярным давлением.

Известно, что при механическом уплотнении влажного осадка удается удалить только часть воды, находящейся в нем. При этом предельная сухость осадка, достигаемая при механическом уплотнении, определяется физикомеханическими свойствами частиц осадка. Одним из объяснений этого может быть двойная пористость осадка. Поровое пространство может быть разделено на две части: внешнее поровое пространство и внутреннее поровое пространство. Первое представляет собой пространство между частицами осадка. Второе образовано порами внутри частиц осадка. При построении математической модели будем считать, что частицы осадка не сжимаемы и что количество воды, находящейся внутри них, в процессе механического уплотнения осадка остается неизменным. Также известно, что не вся вода, находящаяся во внешнем поровом пространстве может быть удалена из материала в результате его механического уплотнения. Поэтому ту часть внешнего порового пространства, занимаемого удаляемой механическим путем водой, будем называть активным. Оставшуюся часть внешнего порового пространства и внутреннее поровое пространство – неактивным поровым пространством. Одной из важнейших характеристик пористого материала является пористость m. Активная пористость будем определять по формуле m

^a пор V

, где V пор^а – объем

внешнего порового пространства, занимаемого подвижной жидкостью и воздухом в случае его присутствия в материале, в рассматриваемом объеме V бумажного полотна.

Объем бумажного полотна V складывается из объема воды V 1^а и объема воздуха V 2 во внешнем поровом пространстве, объема частиц осадка V 3 и суммы объема воды, находящейся внутри частиц, и объема неподвижной воды во внешнем поровом пространстве, V 1 ^н

V V ₁^a + V ₁^н + V ₂ + V 3 . (2)

В дальнейшем удобнее вместо пористости m использовать коэффициент пористости. Будем использовать коэффициент активной пористости 8 и предельный коэффициент пористости гlim , определяемые по формулам

V пор   V 1^a + V ₂

V 3

V 3

н

,    еlim    ^{V пор} ,  (3)

V ₃

Активная пористость связана с коэффициентом активной пористости соотношением

е

m

1+ 8

.

В процессе прессования осадка в прессовом захвате одновременно с течением воды и воздуха через «скелет» осадка происходит деформирование и самого «скелета» в результате переупаковки образующих его частиц. Поэтому для описания течения воды и воздуха в деформируемом осадке будем использовать уравнение Дарси-Герсеванова [1]

u ₁    u ₃

k ₁ (1 + 8)5 p

к¹ 1 ^-(Р1 •8 Э ^z

„     _ k2-(1 + Ю ^p u2   u3                     ,

22   ^z

где: u1, u2   скорости воды, воздуха и частиц осадка, отнесенные к занимаемой

ими части поперечного сечения материала; k 1 , k 2 – проницаемости бумажного полотна для воды и воздуха; ф₁,ф ₂ - насыщенность пор водой и воздухом соответственно; 1 , 2 коэффициенты динамической вязкости воды и воздуха; р - гидростатическое давление.

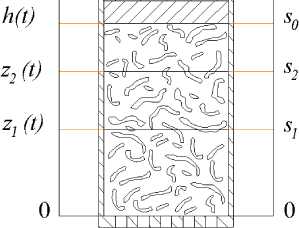
Перемещение верхней границы бумажного полотна затрудняет формулировку граничных условий задачи. Целесообразнее формулировать задачу с использованием лагранжевой массовой координаты. Выделим двумя горизонтальными плоскостями, перемещающимися со скоростями, равными скоростям волокон «скелета», элементарный слой сжимаемого осадка, представляющий собой параллелепипед, высота которого равна dz , а площадь основания 1. В процессе уплотнения полотна величина dz будет изменяться, а масса волокон в элементарном слое будет оставаться постоянной и равной ее начальному (перед действием внешней нагрузки) количеству. Таким образом, эйлеровы координаты z верхней и нижней плоскостей в моменты времени t и t+ t будут разными, а массовые координаты s будут одинаковыми (рис.2).

q(t)

z\ а м мп Р

Массовая координата s связана с координатой z соотношением s          3      dz,                   (7)

0 1 + 8 + 8lim где 3 – плотность частиц «скелета».

Так как

s ₃

д z 1 + 8 + 8_Пт

то уравнения (5 – 6) могут быть записаны

следующим образом

u ₁

^k 1   3     ^p

^, i ^s

^k 2   3        ^p ,             (10)

/£ ■ (1- ф)- 8 Ss

где и 1 , и ₂ - скорости воды и воздуха относительно волокон «скелета».

В рассматриваемом элементарном слое содержится масса волокна ds, масса воды, находящейся в активном поровом пространстве, dМ1         1 ds                (11)

и масса воздуха dM2= 8-(1-Ф)* — -ds.          (12)

За промежуток времени dt из рассматриваемого слоя через его нижнюю границу вытекает масса воды, равная Pi • u1 -m-tp -dt,                    (13)

а через верхнюю границу поступает масса воды, равная

f d

p i* ui mi-(p-\ --( ui m* ф)- ds dtt . (14)

s

В результате за промежуток dt в рассматриваемом слое увеличение массы воды составит

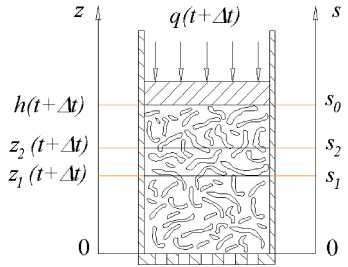
Рисунок 2 - Схема к пояснению перехода к массовой координате

a , „ _ x ,

—(fl-urm-(p)-dsdt =

s

^k 1    1    3         ^p

(15) ds dt.

a s(^-(i+£+£iim) a s)

С другой стороны это увеличение будет равно

a

6 P1 , — а-ф-¹ - ds -dt .

t

Приравнивая выражения (15) и (16), получим уравнение, описывающее течение воды в бумажном полотне,

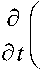
Pl

s

^k 1    1    3          p

1 ⁽¹           lim ^{)     s}

Аналогичным образом

можно по-

ные фазовые проницаемости осадка для воды и воздуха соответственно.

Абсолютная проницаемость зависит только от пористости бумажного полотна. Эта зависимость может быть представлена в виде

лучить уравнение для воздуха

t

( 1      )      ²

s

^k 2     2    3

2 ^{( 1}           lim⁾

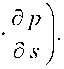
k_а   k ₀

¹          lim

1      0       lim

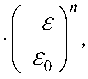
Для преобразования этих уравнений к более удобному для решения виду воспользуемся фильтрационно-компрес-

где k 0 – абсолютная проницаемость осадка перед прессованием, n – фильтрационный коэффициент.

Относительные фазовые прони-

сионными характеристиками осадка и уравнением состояния воздуха. Коэффициент пористости зависит от эффективных напряжений в «скелете» осадка. Эту

цаемости зависят от насыщенности пор соответствующими компонентами и могут быть представлены в виде

kфi

зависимость, называемую компрессионной характеристикой осадка, можно представить в виде

0 е , (19)

где 0 –коэффициент активной пористости осадка перед прессованием, – коэффициент сжимаемости; σ – эффективное напряжение в «скелете» осадка, рав-

3 , 5

i       кр i

1        к р i

i 1 , 2 ,

где кр i – критическая насыщенность материала i -й фазой, т.е. такая насыщенность i -й фазы при которой ее движение

прекращается.

Уравнение состояния воздуха при изотермической фильтрации будет иметь

вид

ное q – р .

Решение поставленной задачи осложняется также тем, что сжимаемый осадок не является абсолютно упругим

2 а

р  ра ра

материалом и при полном снятии внешней нагрузки восстанавливается не полностью. Примем, что разгрузка осадка, которая начинается при уменьшении эффективного напряжения, описывается

где а – плотность воздуха при атмосферном давлении р а .

Используя приведенные выше соотношения, уравнения (17) и (18) можно

записать в виде

уравнением

8 = s o-e" a" °.(20)

Параметры разгрузочной кривой определяются по формулам

n min max

0     min e        ;(21)

max min     0 e, где max – максимальное эффективное напряжение, достигаемое в данной точке осадка на стадии уплотнения.

Проницаемость осадка для воды и воздуха может быть представлена в виде ki=ka■kфi,        i = 1, 2, где: ka – абсолютная проницаемость бумажного полотна; kф1, kф2 – относитель-

S2 pS a             101

3  T0             3

8 ^

^k ф1       1   3 ⁿ

A

... а            ¹

( 1      )

a-

2   ^S 0²

^...         3    ^T 0

8 ^

5 r

S0

T 0

q

;

a pa

8tp _

....

S ₀

T

T ₀

^k ф 2        2   3    ⁿ

...            ₂

( 1     )     S 0²

3      T 0

p

8 ip

p

8 т

5 ip

q

,

...   (26)

где – постоянная величина, характеризующая свойства конкретного осадка перед прессованием и равная

M i 0,5 u       L

h

M i 0 , 5 M i 0 , 5

h

ui    ...

k ₀

8n -(1+ a- f_lim)

.

Для удобства решения данная система записана в безразмерных перемен-ts ных       ,          ,где 2Т0 – продол-

T ₀         S ₀

жительность прессования.

Введем следующие обозначения:

M

...■ ^{i 0} ' 5 -гч ₊i= - LtU-Ni-qq,       (30)

h где h =    2/   ; ǔi – значение неизвест ной переменной в i ой точке в момент времени ; ui – значение неизвестной переменной в той же точке в момент времени +   ; q – приращение внешней нагрузки за промежуток времени .

Обозначим

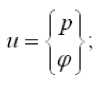
A i

M i 0 , 5

h

;

B i    L i

M i 0 , 5   M i 0 , 5

h

;

Di =-Li-Ui-Ni- qq.

•Pi ’P.S

Тогда система уравнений (25  26)

может быть записана в матричной форме

Тогда в конечно-разностной форме система уравнений (29) примет вид

A ₁ u ₀   B ₁ u ₁    А ₂ u ₂    D ₁ ,

A ₂ u ₁   B ₂ u ₂   А ₃ u ₃    D ₂ ,

^A i ^u i 1    ^B i ^u i    ^А i 1 ^u i 1    ^D i ^,

A N 2 u N 3 B

... + А

N 1 u N 1

N 2 u N 2 D N 2 ,

u   uq

L  MN.

u

q

d т dip

d T

Полученная система уравнений может быть решена методом конечных разностей. Воспользуемся консервативной разностной схемой, для построения которой используем интегро-интерполяционный метод. Применяя чисто неявную схему, обеспечивающую абсолютную устойчивость и монотонность при любом соотношении шагов по и и равномерную сетку, состоящую из N узлов, систему уравнений (29) можно записать в виде

A N 1 u N 2   B N 1 u N 1

... + ^A N u l^ = DN _1 .

Для решения системы уравнений, описывающей обезвоживание бумажного полотна, ее необходимо дополнить двумя уравнениями, учитывающими граничные условия. Рассмотрим половину ячейки, граничащей с проницаемой нижней поверхностью (рис.3).

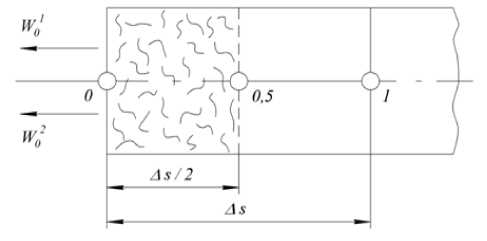
Рисунок 3 - Схема граничного элемента слоя материала

В выделенном элементе содержится массовое количество воды, равное

s

⁽ ^о— ,

2     3

в него поступает за промежуток времени t массовое количество воды, равное

( u ₁ m        ₁)_{0 , 5} t

^k ф 1     1     3     ⁿ

а вытекает W 0⁰    t .

Уравнение баланса для ного элемента будет иметь вид

0 , 5

t,

B 0

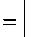
0 B ₀₀

⁰ B ₁₀

B ₀₁

B ₁₁

выделен-

s

(       )                 1

t             2

kф1    1   3 n

S ₀

...   2

1 ( )0

(  2)

₁ (        ) ₀    C ₀ ⁰ ₀

( 1      ) (     2 ^а )      ...C 1⁰0

p_{а 0}

s

0 , 5

W ⁰ .

Используя компрессионную характеристику материала и безразмерные переменные, можно переписать это уравнение в следующем конечно-разностном виде

А 1

_А 00    _А 01

_А 10    _А 11

^k ф 1    1   3     ⁿ

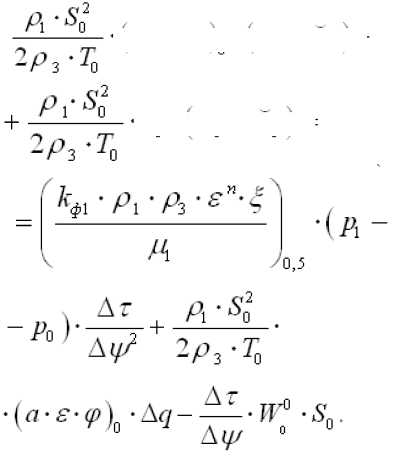
•(л*5" И Ч^о -А)+

-^ • ^о -№ .) =

Аналогично, рассматривая баланс воздуха в выделенном элементе, можно получить уравнение

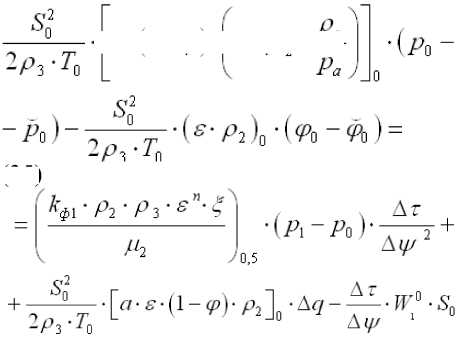
В матричной форме эти уравнения

• £-(1-<р)- а-рр—-

можно записать так

B0 u0  А1 u1  D0  X0, где

Д т

0 , 5

k_{ф 2    2   3}

0 , 5

D        ^{S 0}      ...

⁰     2   3 T 0

' /? 1 [(а 8ф^р\p 0+ Aq )

(   (1     ))0

- (8 p)V ф

u ₀

X 0

+ ⁽ 6ф ) о ]

a pa  0

^^

p ₀    ...

...   (        ₂)₀

p ₀

;

u ₁

p ₁

X 0⁰

X 1⁰

S ₀

W 0⁰

W ⁰

.

Аналогичным

образом можно

записать и уравнение, учитывающее граничное условие на верхней по верхности бумажного полотна. В общем случае, учитывая возможность прессования между двух сукон, это уравнение будет иметь вид AN uN 1 BN uN  DN  XN ,

где

AN

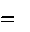
00 A_N

10 A_N

kФ2

BN

01 A_N

11 A_N

1           N 0,5

00 B_N

10 B_N

² S ₀

2   3 T 0

01 B_N

11 B_N

1           N 0,5

1-(a- еф) , ■

_{A 0} 0 ₀

s (1-ф)- (a- pp- а) )  + ^

pа N

D N

S

2 3^0  * ^/"'^(l   Ф)) n-

pN uN         ; uN 1

N

^p N 1 ;

N 1

P i Че) n - ( XV e) n

P [(» 5ф) N ( p n+ Д ? )(5ф) N ]

₂ ^a

XN

В случае прессования с одним сукном, когда верхняя граница бумажного полотна соприкасается с непроницаемой поверхностью верхнего вала пресса, потоки W 0 ^N и W 1 ^N будут равны нулю. После добавления в систему уравнений (32) уравнений (36) и (37) система примет вид

B0 u0  A1 u1  D0

A1 u0  B1 u1  A2 u2

A2 u1  B2 u2  A3 u3

p a _N

XN

¹ X_N

' p N + ( ^ P-) ) N

• Aq-⁽S p, ) N -Ф N ;’

A i u i 1    B i u i    A i 1 u i 1    D i ,

21 ^s .

S ₀

W N ⁰

^W N ^{1 .}

ним нижним

ношение k2ф    2

₀     2 ф    2

сукном используется соот-

X 0¹     0 Х 0⁰ ,

где

k _{1 ф    1}

.

Данное соотношение получено на основании следующих определений для удельных массовых потоков воды и воздуха на нижней границе бумажного полотна

W 0¹

W 0²

k ₁

k ₂

p s

^, 0

2   ⁽¹           lim ⁾

Таким образом,

.

s ₀ полученная сис-

A N 2 ^u N 3 B N 2 ^u N 2 A N 1 ^u N 1   D N 2 ^, тема содержит  2( N +1)  уравнений и

A N 1 u N 2   B N 1 u N _c 1   A N u N D N ,

A N u N 1 B N u N   D N   X N .

На границе прессового сукна с бумажным полотном давление будем считать давление заданым. При решении рассматриваемой задачи прессования с од-

столько же неизвестных: Х 0⁰ , φ 0 и р i , φ i ( i = 1,2, … , N ). Матрица системы имеет диагональную форму с шириной ленты 5 и система может быть легко решена методом Гаусса.