Математическая модель финансирования системы образования в форме задачи оптимального управления и ее применение

Образование является одной из основ человеческого капитала и играет решающую роль в его формировании. Качественное образование выходит на приоритетный уровень как фактор развития общества, занимающий важное место в инновационной экономике. Однако в системе образования существуют проблемы, которые не позволяют ей работать с максимальной полезностью: неадаптированный переход на европейские стандарты, слабая взаимосвязь между уровнями образования, недостаточное финансирование. Образование – это сфера, где разрабатываются новые подходы к управлению, направленные на повышение социально-экономической эффективности и динамичное развитие. Инстру-

Чернова Екатерина Сергеевна кандидат физико-математических наук, доцент. Кемеровский государственный университет, город Кемерово. Сфера научных интересов: теория оптимальных процессов; теория игр; математическое моделирование социо-эколого-экономических систем. Автор более 30 опубликованных научных работ.

ментом для создания таких подходов может стать математическое моделирование, позволяющее разрабатывать количественно обоснованные методы принятия решений.

Актуальность вопроса разработки математической модели

С 1960 годов построению математических моделей проблем в сфере образования было посвящено большое количество работ. Условно их можно разбить на две группы:

• -    микромодели, описывающие образовательный процесс и процессы принятия решения в конкретных учебных заведениях;

• -    макромодели, разрабатываемые для изучения систем образования в отдельных экономических регионах и государствах.

К первой группе относятся работы, посвященные следующим вопросам: построение задачи оптимизации курса конкретной учебной дисциплины [11]; оптимизация учебного процесса при долгосрочном планировании [8]; определение взаимосвязи дисциплин учебного плана методами математической статистики [8]; вычисление оптимальной образовательной траектории студента при помощи метода динамического программирования [6]; построение комплексных оценок компетентности выпускников вузов [1].

Ко второй группе можно отнести работы, посвященные применению математических и имитационных моделей для исследования систем профессионального образования конкретных регионов (например, [2; 7; 12]), теоретико-игровому моделированию взаимодействия университетов [13].

Однако среди существующих работ нет достаточного количества исследований, посвященных моделированию региональных систем образования с учетом их специфики. В данной статье предлагается построить математическую модель, относящуюся ко второй группе, и с ее помощью сформулировать алгоритм расчета стратегии развития образовательной системы. К анализу проблемы предлагается подойти с позиций теории графов и теории оптимальных процессов.

Построение математической модели функционирования системы образования

За основу для построения взята модель социальной системы [3] и предложена модификация модели, описанной в работе [5].

Принимая во внимание наличие необходимых для исследования данных, представим структуру системы образования в виде совокупности взаимосвязанных классов: C ₁ – об-

Математическая модель финансирования системы образования ...

щее образование (далее – ОО); C ₂ – среднее профессиональное образование (далее – СПО); C ₃– высшее образование (далее – ВО); C ₄– класс людей, которые закончили одну из ступеней образования и не пошли учиться дальше либо не достигли возраста для получения общего образования.

Пусть система функционирует на протяжении периода времени [0, Т ], разбитого точками 0,1,2, …,T , где шаг – отрезок, равный году. Структуру системы представим в виде ориентированного графа, изображенного на Рисунке. Наличие дуги ( i , j ) определяет возможность перехода между классами с номерами i и j . Считается, что на переход человека из класса в класс влияет распределение бюджетных средств по различным сферам финансирования.

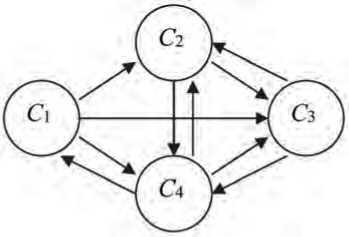
Рисунок. Структура системы образования

Пусть x_i ( t ) – численность людей в классе C _i в год t ; f _ij( u ( t )) – численность людей класса C _i, переходящих в класс C _j, где u ( t ) = ( u ₁( t ), …, u ₈( t )) – вектор денежных отчислений в различные сферы: u ₁ – культура и кинематография, u ₂ – национальная экономика, u ₃ – ОО, u ₄ – СПО, u ₅ – ВО, u ₆ – профессиональная переподготовка, u ₇ – социальное обслуживание населения, u ₈ – социальное обеспечение населения.

Модель функционирования системы образования представим в следующем виде:

Xi(t) = Xi(t-1) + £af (u(t))-£af (u(t)) + Yxy(t) , i = 1,...,4,t = 1,...,T, j=1

j * ij

Xi (0) = x0 , i = 1,...,4,

£f(u(t)) 0, i * j , i, j = 1,...,4, t = 1,...,T,

^k

T²

J^(X 0,^u ) = V(f12^(u(t)) ^-Mi3⁽u⁽t ))) ^ min

7=1                                         ^u (')^eU

Модель (1)–(7) – это задача оптимального управления с дискретным временем; (1) – уравнение динамики для расчета численности людей в классе C_i в момент t, где y(t) – прирост населения, определяемый при помощи статистических данных региона; (2) – состояние системы в начальный момент времени, которое описывается численностью людей в каждом классе. Соотношение (3) вводится для отслеживания того факта, что из каждого класса не может выйти учащихся больше, чем в нем находится. Неравенство (4) показывает, что количество людей, переходящих из класса в класс в каждый момент времени, не может быть отрицательным. Ограничения (5) и (6) задают верхние и нижние границы финансирования каждой из сфер и численности объектов в каждом классе соответственно. Критерий (7) отражает минимизацию диспропорции между количеством абитуриентов в учреждениях СПО и ВО, где X - коэффициент пропорциональности; U - множество допустимых управлений в (1)-(7); и(■) = {и(1),..., и(Т)} - управление.

Алгоритм построения стратегии финансирования

Для решения задачи (1)–(7) сформулируем следующий алгоритм.

• 1.    Определение вида зависимостей f_ij(u(t)) на основе статистических данных региона методами регрессионного анализа.

• 2.    Определение констант X, T, pt, S, а*, Pi , k = 1,...,8, i = 1,...,4, t = 1,...,T (в том числе экспертным путем).

• 3.    Определение начального состояния (2) из статистических данных региона.

• 4.    Методом исключения фазовых переменных сведение (1)–(7) к статической оптимизационной задаче.

• 5.    Определение оптимальных значений параметров и(■) = {и(1),...,и(T)} с помощью пакета поиска решения MS Excel на рассматриваемом отрезке времени.

Расчет оптимальных управлений на основе статистических данных РФ

Для проведения расчетов использовались данные по расходам бюджета РФ, численности обучающихся на каждой ступени образования и числе переходов между ступенями, а также движению населения, взятые из официальных источников, например, [10].

Для реализации первого шага приведенного алгоритма в качестве зависимой переменной использовалась численность переходов из класса в класс, а в качестве факторной – расходы бюджета по статьям. Вид функций f_ij(u(t)) был определен с помощью инструмента множественной регрессии пакета Statistica, при этом применялась процедура пошаговой регрессии с включением. В результате были получены следующие зависимости:

f₁₂(u) = 15,37и7 + 357,62 ; f₁₃(u) = 0,04и1 + 9,21и₂ + 3,82и₆ + 77,44 ;

f₁₄(u) = 0,03и₃ + 0,45и5 + 0,06и₈ +16,07 ;

f₂₃(u) = 5,84и1 + 8,31и7 +139,80 ; ^4(и) = 9,17и1 + 13,05и8 + 219,58;          (8)

f₃₄(u) = 0,03и₄ + 17,90и7 + 747,20 ;

f41(u) = 34,04и₇ +1192,46 ; f₄₂(u) = 30,78и₇ + 858,66 ;

f₄₃(u) = 8,35и₇ +1088,54 .

Для реализации второго шага алгоритма предположим, что горизонт планирования – 6 лет, то есть T = 6. Значение X определим по формуле

Математическая модель финансирования системы образования ...

T

xL

t-1

f₁₂(u(t))

^f13^(u(t)) ’

где в качестве u(t) рассматривались реальные значения бюджетных отчислений за период

2013-2018 годов. Значение X составило 5,52.

Для определения констант неравенства (5) для каждой сферы были определены граничные значения фактических расходов за рассматриваемый период времени. Ограничения сверху на численность классов не вводились. Нижняя граница принималась равной нулю.

На третьем шаге в качестве начального состояния системы была взята численность в классах в 2012 году, тыс. чел.:

^1(0) -15219 ; x₂(0) - 2852 ; x₃(0) - 4498 ; x4(0) -123975 .

На четвертом этапе задача (1)–(7) была сведена к задаче математического программирования, где в качестве неизвестных выступают u_t (t), k = 1,...,8, t - 2013,...,2018, в качестве целевой функции – выражение (7), а соотношения (1)–(6) играют роль ограничений.

На пятом этапе для реализации расчетов было построено начальное приближение для финансирования, которое удовлетворяло ограничениям. Оптимальные величины расходов приведены в Таблице 1.

Таблица 1

Расчетные значения расходов бюджета РФ по статьям, млрд руб.

Таким образом, найден оптимальный для финансирования образования вариант распределения расходов бюджета РФ. Далее проведем аналогичные расчеты для конкретного региона и сравним результаты.

Расчет оптимальных управлений на основе статистических данных Новосибирской области

Для проведения расчетов по Новосибирской области использовались данные, взятые из [9].

Зависимости f_ij(u(t)) получены в следующем виде:

f₁₂(u) = 0,0005u3 + 2,69 ; f₁₃(u) = 0,02u₅ + 9,10 ; f₁₄(u) = 0,00004u₅ +1,19 ;

f₂₃(u) = 0,0007u7 +1,17 ; f₂₄(u) = 0,001u₇ +1,84 ; f₃₄(u) = 0,0001u₈ +14,39 ; f₄₁(u) = 0,0003u₈ + 23,98 ; f₄₂(u) = 0,0006u1 + 0,04u₅ + 0,04u₆ + 23,18 ;

f₄₃(u) = 0,0005u₂ + 0,004u₄ + 39,39 .

Здесь в качестве переменной u₁выступают расходы по статье «Здравоохранение».

Значение X составило 5,38.

Начальное состояние системы в 2012 году x1(0) = 288 ; x2(0) = 39 ; x3(0) = 110 ; x4(0) = 2325 .

Полученные оптимальные величины расходов приведены в Таблице 2.

Таблица 2

Расчетные значения расходов бюджета Новосибирской области по статьям, млн руб.

Таким образом, был найден оптимальный для финансирования образования вариант распределения расходов бюджета Новосибирской области.

Анализ полученных результатов

Перед анализом полученных результатов по расходам бюджета РФ в целом и отдельно по Новосибирской области сравним зависимости (8) и (9) для численностей людей, переходящих из класса в класс, от расходов бюджета.

Рассмотрим сначала переходы из организаций общего образования в другие классы модели. Численность переходов в организации СПО в РФ зависит от расходов на социальное обслуживание населения, тогда как в Новосибирской области – от финансирования общего образования. Для переходов в учреждения ВО по РФ наблюдается зависимость от расходов на профессиональную переподготовку, национальную экономику и культуру, в то время как в Новосибирской области – от финансирования высшего образования. Для численности переходов в класс людей, не занятых в образовательном процессе, в анализе данных по РФ наблюдается зависимость от таких статей расходов, как «Высшее образование», «Социальное обеспечение населения» и «Общее образование», тогда как в Новосибирской области – только от расходов на высшее образование.

Далее проанализируем переходы из класса обучающихся в учреждениях СПО в оставшиеся классы. Численность людей, переходящих в организации ВО, в РФ зависит от фи-

Математическая модель финансирования системы образования ...

нансирования социального обслуживания населения и культуры, а в Новосибирской области – только социального обслуживания населения. Количество переходов в класс не занятых в образовательном процессе в РФ зависит от расходов на социальное обеспечения населения и культуру, а в Новосибирской области – только на социальное обслуживание населения.

При переходе из класса обучающихся в учреждениях ВО в класс людей, не занятых в образовательном процессе, по РФ наблюдается зависимость от расходов на СПО и ВО, а по Новосибирской области – на социальное обеспечение населения.

Наконец, рассмотрим переходы из последнего класса не занятых в образовательном процессе в три других возможных класса. Для переходов в организации общего образования по РФ наблюдается зависимость от расходов на социальное обслуживание населения, а в Новосибирской области – на социальное обеспечение населения. Численность переходов в учреждения СПО, по данным о расходах бюджета РФ, зависит от финансирования социального обслуживания населения, в то время как в Новосибирской области – от высшего образования, здравоохранения и профессиональной переподготовки. Переход в организации ВО для РФ зависит от финансирования социального обслуживания населения, в Новосибирской области – от национальной экономики и СПО.

Сравнив соотношения (8) и (9), полученные для РФ и для Новосибирской области, можно сделать вывод, что совпадений между факторами, от которых зависит численность переходов между классами, не наблюдается. По отдельным статьям расходов это можно заметить только в случае переходов f₁₄ из класса обучающихся в общеобразовательных учреждениях в класс людей, не занятых в образовательном процессе, и f₂₃ – из класса обучающихся в учреждениях СПО в класс обучающихся в ВО. В первом случае таким фактором являются расходы на высшее образование, во втором – на социальное обслуживание населения. Кроме того, можно заметить, что в целом по РФ одним из важных факторов, влияющих на повышение уровня образования, являются расходы на социальное обслуживание населения, а также по статье «Культура и кинематография». Для Новосибирской области таким фактором являются расходы на высшее профессиональное образование наряду с финансированием социального обслуживания и социального обеспечения населения.

Сравним полученные значения расходов бюджета с фактическими данными. Для РФ результаты приведены в Таблице 3.

Таблица 3

Разность между фактическими расходами бюджета РФ по статьям и полученными расчетными данными, млрд руб.

Отрицательные значения между фактическими расходами и расчетными свидетельствуют о том, что эти расходы следовало бы увеличить. Строки с нулевыми значениями в таблице не приведены.

На основании Таблицы 3 можно сделать следующие выводы.

• 1.    Расходы по статье «Культура и кинематография» можно сократить в пределах диапазона, приведенного в Таблице 3.

• 2.    Расходы в сферы национальной экономики и профессиональной переподготовки следует увеличить.

• 3.    Остальные статьи расходов бюджета РФ соответствуют оптимальным значениям.

Результаты сопоставления фактических и расчетных данных для Новосибирской области приведены в Таблице 4.

Таблица 4

Разность между фактическими расходами бюджета Новосибирской области и полученными расчетными данными, млн руб.

На основании данных Таблицы 4 можно сделать следующие выводы.

• 1.    Расходы в сферу ОО следует увеличить в пределах суммы, приведенной в Таблице 4.

• 2.    Расходы в сферу ВО можно сократить.

• 3.    Остальные статьи расходов бюджета Новосибирской области соответствуют оптимальным значениям.

Выводы

Таким образом, для определения оптимального варианта финансирования образования следует проводить расчеты по каждому региону в отдельности, так как в них поток финансов и учащихся индивидуален.

Необходимо отметить, что полученные численные значения расходов бюджета сильно зависят от тех исходных предположений, которые вводятся при реализации второго этапа предложенного алгоритма. Кроме того, при определении оптимальных расходов по статьям, связанным не только с образовательной деятельностью («Национальная экономика», «Культура и кинематография», «Здравоохранение» и др.) необходимо учитывать, что они оказывают влияние и на другие сферы устойчивого развития общества.

Исходя из проведенного исследования особое внимание при планировании бюджета следует обратить на финансирование социального обслуживания населения, которое имеет значимое влияние на численность переходов между различными классами системы образования как на федеральном, так и на региональном уровне. Также при дальнейшем планировании бюджета на уровне РФ необходимо сделать акцент на расходы в сферах национальной экономики, культуры и кинематографии, профессиональной переподготовки, а на уровне Новосибирской области – в сферах общего и высшего профессионального образования.