Математическая модель формообразования зубчатых изделий объемным инструментом с одним параметром движения

УДК 621.7.074                                             

Введение. Рассматривается процесс формообразования боковой поверхности зуба колеса передачи Новикова с использованием следующего алгоритма:

• —    описывается производящая поверхность инструмента в системе координат этого инструмента;

• —    реальная поверхность зубьев колеса формируется как огибающая производящей поверхности инструмента при движении последнего относительно колеса с независимыми параметрами;

• —    проводятся численные исследования по отклонению реальной поверхности от теоретической и анализ полученных результатов.

  
  

В соответствии с ГОСТ 13 755–81 для режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются для зубчатых колес параметрами исходной рейки через параметры ее нормального сечения — исходный контур. В качестве инструмента в работе рассмотрен шлифовальный круг.

Относительное движение звеньев передачи или инструмента и заготовки при обработке можно описать одним или двумя независимыми параметрами. Поверхность зубьев первого звена является огибающей однопараметрического или двухпараметрического семейства поверхностей второго звена. Очень часто поверхность зубьев изделий в процессе его обработки формируется как огибающая производящей поверхности инструмента при движении последнего относительно изделия с одним независимым параметром. В большинстве случаев в качестве такого параметра выбирают угол поворота изделия.

Теоретическая поверхность зубьев колеса в процессе его финишной обработки абразивным инструментом формируется как огибающая производящей поверхности инструмента при движении последнего относительно колеса с независимыми параметрами. Теоретической поверхностью, в соответствии с ГОСТ 16 530–83, является каждая из двух поверхностей (боковые поверхности двух зубьев), обеспечивающие при их взаимодействии заданное передаточное отношение.

В связи с вышеизложенным была поставлена задача по определению уравнений боковой поверхности зубьев изделия. Поверхности образованы с помощью инструмента, осевой профиль которого совпадает с исходным контуром. При этом инструмент совершает движение вдоль оси изделия, а колеса — согласованное вращение вокруг своей оси. Так как вращение изделия и перемещение инструмента связаны между собой аналитической зависимостью, то в качестве независимого параметра формообразования зубчатого изделия выбран угол поворота изделия φ к .

Материалы и методы. Для получения уравнения номинальной производящей поверхности инструмента в работе была использована система координат, жестко связанная с рейкой. В качестве исходного контура принято нормальное сечение рейки. На рис. 1 в качестве примера показан обобщенный исходный контур, взятый из исследовательских работ [1, 2]. Контур составлен из дуг окружностей, которые могут плавно сопрягаться между собой или пересекаться, что зависит от типа исходного контура.

На рис. 1 цифрами в кружках показаны номера участков ( i =1,2,3,...7). Границы участков выделены крупными точками. Кроме этого, на рис. 1 приняты следующие обозначения: S i (X i ;Y i ;Z i ) системы координат, связанные с i -тым участком исходного контура. Начало координат такой системы совмещено с центром окружности участка, а направление осей совпадает с направлением осей системы координат рейки S p (X p ;Y p ;Z p ).

Решение задачи разбито на два этапа. На первом этапе строится математическая модель объемного инструмента в виде тела вращения (например, дискового шлифовального круга или дисковой фрезы). На втором этапе с помощью инструмента формообразуется зубчатое изделие с одним независимым параметром движения.

Математическая модель инструмента

Получим теоретическую производящую поверхность, привязав поверхность инструмента с системой координат S и (Х и ;Y и ;Z и ) , направив ось Z и вдоль оси вращения инструмент. Ось Х и расположим таким образом, чтобы она проходила через расчетную точку, в качестве которой принимаем точку касания инструмента и изделия в начальный момент времени. Ось Y и направлена так, чтобы все оси составляли правую декартовую систему координат. С исходным контуром связана собственная система координат S р (Х р ;Y р ) , оси которой расположены так, чтобы ось Z p совпадала с делительной прямой исходного контура, а ось X p , была ей перпендикулярна и направлена в сторону оси инструмента.

Для формообразования производящей поверхности инструмента применяются устройства, работающие с помощью копира, либо устройства, воспроизводящие траекторию движения правящего алмаза или заточного инструмента с помощью системы ЧПУ. Для любого из этих случаев математическое описание производящей поверхности инструмента будет однотипным 1, 2 [3].

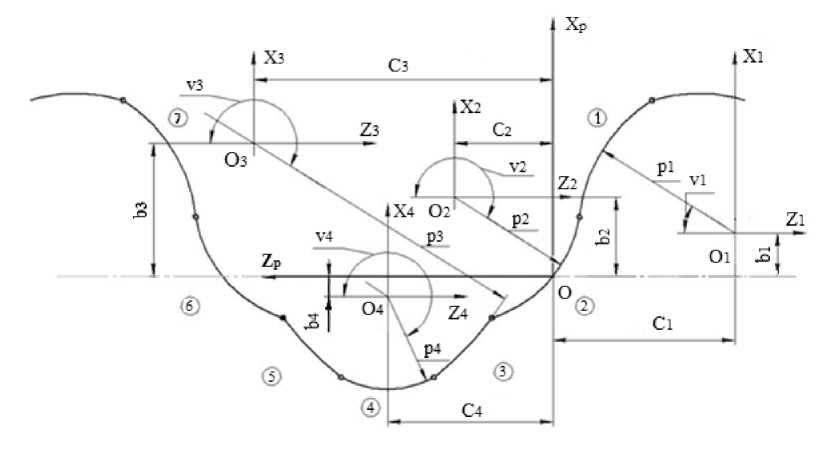
Рис. 1. Исходный контур ДЛЗ-0,7-0,15

На рис. 2 показано взаимное расположение инструмента 1, исходного контура 2, копира 3 , схемы

Машиностроение и машиноведение

• ¹    Кривошейкин, А. В., Нурмухамедов Л. Х., Перелыгин С. В. Математическое моделирование в приборных системах : учеб. пособие. СПб.

2019. 108 с.

• 2    Зюзьков, В. М. Математическая логика и теория алгоритмов : учеб. пособие. Т. 2015. 236 с.

правильного устройства и принятые системы координат, связанные с копиром и инструментом.

Математическую модель производящей поверхности инструмента будем рассматривать как след движения контура копира при его вращении вокруг оси Z и с угловым параметром движения φ и .

В системе координат S p уравнение профиля копира, включающие участки 1, 2 и 3 можно записать следующим образом:

Xp

^Z р

= pt • sin u + Ьрл = pt • cos ut + ct;y

где обозначение величин взяты из работ [4–6]: ρ i — радиус кривизны i -го участка нормального профиля зуба рейки; υ i — криволинейная координата производящей поверхности рейки, начало отсчета которой идет по часовой стрелке от оси Z_р ; с i — аппликата положения центра кривизны соответствующего участка в системе S p ; b i — абсцисса центра кривизны соответствующего участка в системе координат S p .

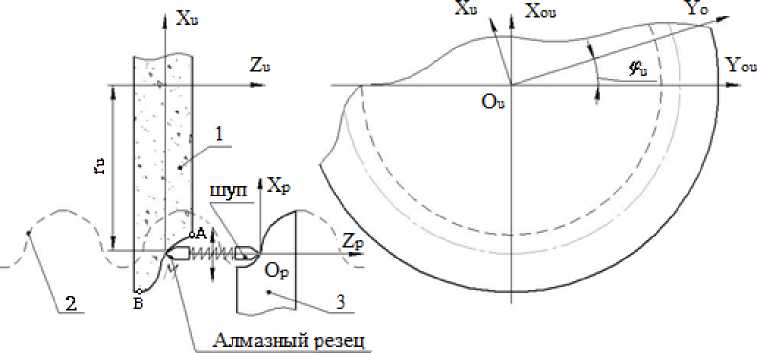
Рис. 2. Схема формообразования инструмента с принятой системой координат

Кроме этого на рис. 2 обозначен расчетный радиус инструмента r и .

Воспользовавшись выбранными системами координат, введенными обозначениями и методикой формообразования поверхностей 3 , получим уравнение производящей поверхности инструмента в проекции на оси координат:

Г X и t = cos р и t • (P t • sin U t +b t - r _u );

Г Й = j^ t = — sin р и t • (p t • sin U t +b t - Г ); I         Z и t = ^-p t • ^{cos u} t ^{- c} t .

Для получения математической модели изделия понадобится уравнение нормали к производящей поверхности инструмента. Поэтому, используя известную методику  [3] и опуская промежуточные преобразование, запишем уравнения орта нормали к производящей поверхности в следующем виде:

ex и t = - cos С и • sin ut; eyиt = sinpи •sinut; ez и t = cos Ut.

i

Математическая модель изделия

Геометро-кинематическая схема формообразования боковой поверхности зуба изделия с помощью инструмента с соответствующими системами координат показана на рис. 3. Участки производящей поверхности инструмента заданы в системе координат S и (X и ; Y и ; Z и ) , жестко связанной с инструментом. Система координат S к (X к ;Y к ;Z к ) жестко связана с обрабатываемым изделием (например, зубчатым колесом). Неподвижные вспомогательные системы координат колеса S o _и (X o _и;Y o _и;Z o _и) и инструмента S o _к (X o _к;Y o _к;Z o _к) , связанные со стойкой.

В качестве независимого параметра относительного движения при обработке изделия примем величину φк, численно равную углу поворота колеса вокруг оси Zк. Перемещение инструмента вдоль оси изделия обозначено как So. Угол наклона линии зуба изделия — βк. Межосевое расстояние — a=ru+rk+Xk.

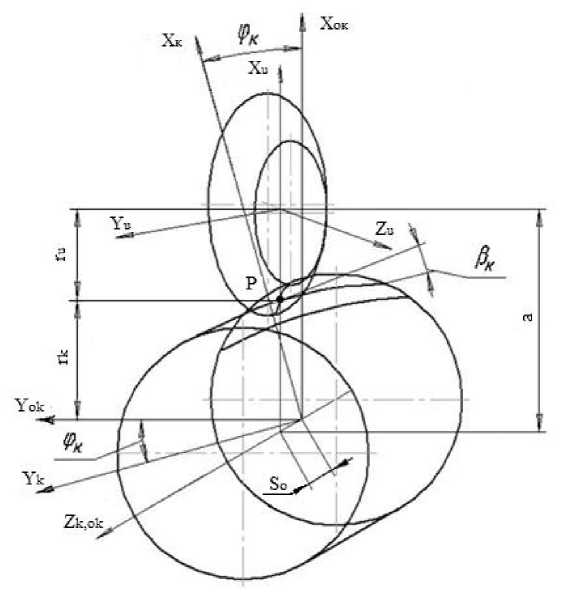
Рис. 3. Геометро-кинематическая схема формообразования профиля зуба изделия инструментом

Реальная поверхность зуба изделия, как огибающая однопараметрического семейства производящей поверхности инструмента, определяется следующим уравнениями [3]:

Т = А ки t • Т и ёщ • V t — 0

^а)1 б)} ,

где т и — матрица-столбец, составленная из проекций производящей поверхности инструмента, записанной в системе координат S_u ; А _{ки t} — матрица перехода от системы координат S_u к системе координат S_к ; V _{u t} — аналог

вектора относительной скорости по параметру фи; ё^ — орт нормали к производящей поверхности инструмента, проекции которого на оси координат Xи, Yи, Zи представлены уравнениями (3).

Матрицу перехода А _{ки t} найдем воспользовавшись методикой изложенной в работах [3, 7]. Опуская промежуточные преобразования, данную матрицу представим в следующем виде:

А ки t =

cosф к - sin ф к

sin Рк  • sin фк sin Рк  • cos фк cos Рк

„     Ф к '^тк

0 — tanpк — а — ^К + Хк + ru

—

—

cos Р к • sin ф, cos Р к  • cos ф,

1 0

' к

' к

Ф к -m-z_K

2 • sinРк

= j^ _{+ x +г} .

2•cos/? _к      ^к     “

а • cos Ф и t ^-а • sin^? и t S_o

)

Воспользовавшись методикой однопараметрического формообразования поверхностей [3], принятыми

системами координат и геометро-кинематической схемой формообразования (рис. 3), а также опуская

промежуточные преобразования, уравнение реальных поверхностей зубьев изделия можно записать так: х к t — cos Ф к • cos Ф и • sin Р к • sin Ф к • sin Ф и • ⁽ P t • sin V t +b t - Т) +>

+ cos Р к • sin Ф и • ⁽ P t • cos V t + C t )

у _K t — sinф к • cos ф и • sinф и • sinР к • cos ф к • (P t • sinv t + b t - Т и ) +

+ cos Р к • cos ф к -(Prcosv t + с t ) z к t — - cosР к • sin Ф и • ⁽ P t • sinv t + b t - т и ) --sinР к • ⁽ P t • cosv t + C t ⁾ -фk■т _k■ ctgР к

Используя методику получения уравнения зацепления (4 б) 4 , окончательно запишем его в следующем

виде:

Машиностроение и машиноведение

cos^K • [sin

^-co sV i ' ( ^r fc ^+X fc ^)] = 0

где X_к — смещения исходного контура.

Результаты исследования

Для определения величины погрешности формообразования профиля изделия с помощью инструмента был использован следующий алгоритм:

• 1.    Реальная и номинальная поверхности зубьев изделия записывались в одной системе координат. В качестве номинальной поверхности зубьев изделий были взяты уравнения боковой поверхности зубьев колеса, образованных с помощью рейки 5 [3].

• 2.    Задавалось текущее значение независимого параметра υ j , где j =1, 2, 3-n — текущий номер точки на профиле зуба колеса.

• 3.    Принимая Z_к i = const , определялось значение второго независимого параметра φ_к j номинального профиля изделия.

• 4.    Через текущую точку υ j профиля зуба изделия проводилась окружность, определялось её пересечение с реальным профилем зуба изделия.

• 5.    В качестве погрешности формообразования принималось расстояние по хорде между точками номинального и реального профиля, расположенных на одной и той же окружности.

Разработанный алгоритм по определению погрешности формообразования был реализован в виде программы в программной среде MathCAD.

В качестве примера на рис. 4 показан характер изменения реального профиля, по сравнению с номинальным, и направление отсчета погрешности Δ ij формообразования профиля зуба колеса передачи Новикова.

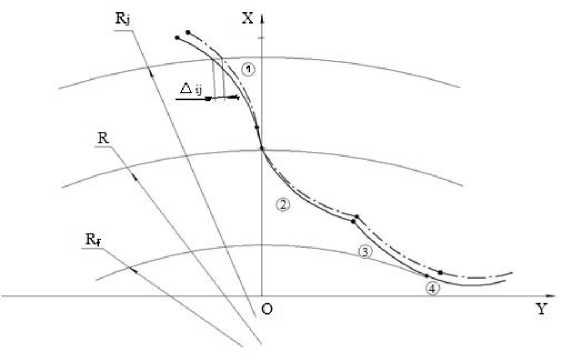
Рис. 4. Характер отклонения профиля зубьев колеса передачи Новикова:

— номинальный профиль;

— реальный профиль

Реальные значения погрешностей Δ ij приведены на рис. 5 для зубчатого колеса передачи Новикова с исходным контуром ДЛЗ 0,7–0,15 и следующими геометрическими параметрами: модуль зацепления m n =5, число зубьев колеса z_к =50, угол наклона линии зуба β_к =20º, смещения исходного контура X_к =0.

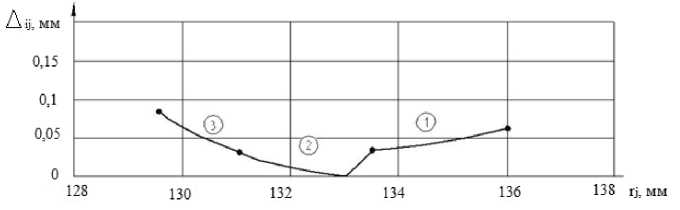
Рис. 5. Отклонение реального профиля от номинального для зуба колеса передачи Новикова

• ⁵ Зюзьков В. М. Математическая логика и теория алгоритмов. 236 с.

Как видно из графика на рис. 5, минимальное значение отклонения находятся в районе делительного радиуса колеса, а максимальные значения наблюдаются на головке и в основании зуба колеса. Максимальные величины формообразования профиля зависят от вида исходного контура, числа зубьев, угла наклона линии зуба, а также от диаметральных размеров инструмента.

Обсуждение и заключения. Разработана математическая модель формообразования зубчатого изделия с помощью инструмента с одним независимым параметром движения.

• 1.    Численные исследования показывают, что по данной схеме обработки невозможно теоретически точно воспроизвести контур зуба изделия, если производящая поверхность инструмента образована по профилю исходного контура обрабатываемого изделия.

• 2.    Максимальные искажения профиля наблюдаются на головке и ножке зуба колеса (у диаметра выступов и впадин) и их величина тем больше, чем выше исходный контур, больше модуль зацепления, меньше число зубьев и больше угол наклона зуба.

• 3.    Для точного воспроизведения профиля зуба необходима корректировка копира, по которому осуществляется правка и заточка инструмента.