Математическая модель и функция преобразования лазерно-телевизионного метода контроля уровня жидкости

В настоящее время во всём мире наблюдается рост количества измерительных устройств, в которых применяется лазерное излучение. Измерения, проводимые с помощью лазерного излучения, содержат в себе ряд преимуществ. Использование лазерного излучения позволяет выполнять измерения с высокой чувствительностью, поскольку вследствие высокой энергетической яркости лазерного луча улучшаются энергетические соотношения в приёмных устройствах. Также, важным фактором в пользу применения лазерного излучения является то, что лазерный луч представляет собой направленное электромагнитное излучение, а скорость распространения электромагнитной волны мало зависит от окружающих факторов, таких как плотность среды, температура, влажность, давление. Известен ряд устройств [1, 2, 3, 4] для измерения уровня жидкости с помощью лазерного луча (одного или нескольких).

Выделим основные параметры измерительного лазерного луча, зависящие от контролируемого уровня жидкости:

-время распространения сигнала от поверхности до приёмника.

-амплитуда и фаза пришедшего на фотоприёмник сигнала.

-спектральный состав сигнала.

раметра с последующей обработкой используется в лазерно-телевизионном методе контроля уровня жидкости).

В данной статье предложены несколько вариантов реализации лазерно-телевизионного метода контроля уровня жидкости, а именно:

• -    по одной лазерной метке;

• -    по двум лазерным меткам, расстояние между которыми заведомо известно;

• -    по N лазерным меткам, расстояние между которыми заведомо известно.

Для пояснения рассматриваемого метода рассмотрим лазерно-телевизионный уровнемер, представленный на рис. 1. Данный уровнемер содержит: телевизионную камеру 1, цифровое вычислительное устройство 2, источники лазерного излучения 3, 4, 5, 6, блок управления 7, блок индикации 8. По команде блока управления активируются источники лазерного излучения, на контролируемой поверхности появляются метки лазерных лучей, а фотоприёмная матрица регистрирует изображение контролируемой поверхности, которое поступает в цифровое вычислительное устройство, где по формулам определяется искомое расстояние H .

Сущность измерительной процедуры в самом общем случае иллюстрируется рис. 1, 2 и состоит в том, что на поверхности жидкости, уровень которой контролируется, с помощью лазерных лучей создаются метки A₁ , A₂ ,… A_i ,… A_n .

Каждая из этих меток имеет координаты в пространстве A_i ( X_i ; Y_i ; Z_i ) . Известно, что все эти точки принадлежат одной плоскости, уравнение которой можно определить через три произвольные точки A_i-1 , A_i , A_i+1 по формуле [5].

X-X i-1

Y - Y i -1

Z

-

Z

i -1

X i

-

X

I +1

X i -1

-

X i-1

Y i ^- Y i -1

Y + i - Y -i

Z i

-

Z + 1

^Zi -1

-

Z i -1

= 0 . (1)

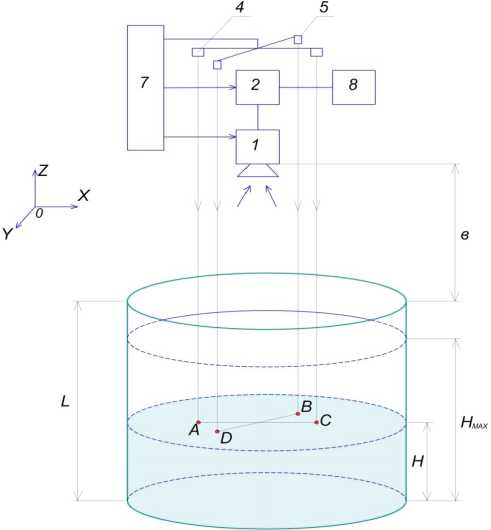
Рис. 1. Структурная схема лазерно-телевизионного уровнемера

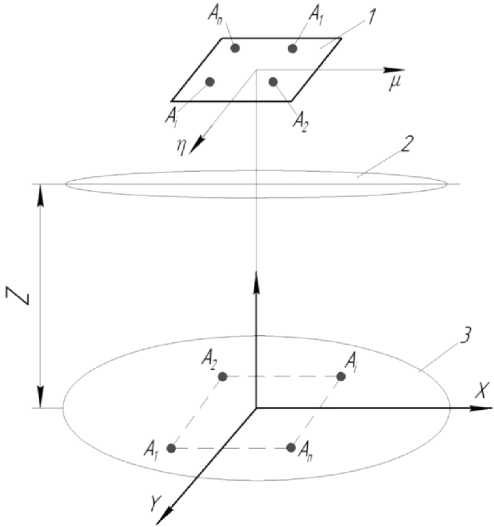
Рис. 2. Иллюстрация к математической модели лазерно-телевизионного метода контроля уровня жидкости:

1 – фотоматрица, 2 – оптическая система, 3 – контролируемая поверхность

Выражение (1) преобразуется к виду

GX + QY + TZ + P = 0 ,      (2)

где

G = (Yi - Yi-,)(Zi+1 - Z-_x) - (Yi+1 - Yi-,)(Zi - ZM), t = (x, - X-1)(Y+1 - Y-1) - (Xw - Xi-1 )(Y - Y-1),

Q = - ( ( x - X -1 )( Z i +1 - Z i -1 ) -( - _м - X -1 )( Z , - Z -1 ) ) ,

P = - GX i - 1 - QY - 1 - TZ i - 1

Предположим, что расстояние между всеми точками известно и определяется по формуле

L n = V ( - . - X ) + ( Y - Y )² + ( Z . - Z )² =

= л / A - ² + A Y ² + A Z ² . n n n

Контролируемая поверхность снимается те-ле(фото)камерой.

Выбранные точки имеют координаты на изображении

А - 1 ^{( ц} / - 1 ; ⁿ г - 1 )’ А ( М / ; ⁿ ii ), А + 1 (M¹ / + 1 ; H + 1 ) .

Из законов геометрической оптики, по правилам сохранения пропорций, при съёмке со стороны Z (центр линзы находится на оси Z ) между координатами точек в пространстве X , Y , Z и на фотоматрице Ц, П справедливы следующие соотношения [6] (при Z >  f )

Ц =

Xf

Z - f ’

п =

Yf Z - f

где f –внешнее фокусное расстояние объектива, для стандартных объективов это величина известная, либо определяется экспериментально. Здесь Z – расстояние от контролируемой повер-

хности до главной плоскости оптической системы, которое связано с контролируемым уровнем Н и другими конструктивными параметрами формулой (см. рис. 1)

,        (6)

где Z m = L + B - высота установки центра оптической системы над нулевым уровнем жидкости, то есть при H = 0, Z = Z m .

Тогда выражения, связывающие координаты точек поверхности и их изображения на фотоматрице будут иметь вид

Ц = Xf          п = Yf .

Zm - H - f ’          2, - H - f ■ (7)

Рассмотрим варианты реализации лазернотелевизионного метода контроля уровня жидкости.

1. Контроль по одной метке. Это возможно, если метка создаётся лазерным лучом, строго параллельным главной оптической оси телекамеры и перпендикулярным контролируемой поверхности. При этом фокусное расстояние известно. В этом случае при смещении уровня вдоль оси Z координаты метки X_i и Y_i не изменяются. Тогда уровень и координаты метки будут связаны соотношениями

Xif                     Yif

Ц Zm - H- f ’     п Zm - H- f (8)

mm

H = Z _m - f • (1 + ),           (9)

μ

„ . Y

H = Z m - f • (1 + ^Y ) .          (10)

n

Из формул (8), (9) видно, что измерения можно проводить по любой координате метки. Для проведения процедуры измерений нужно при известных значениях X_i , Y_i , f, задаться начальным значением координаты метки

Xif

Yif

^{П о} Z - H -f" ⁽¹¹⁾

Z m H 0 f

При изменении уровня координаты метки A i ( ц i ; n i ) на изображении будут смещаться по фотоматрице (рис. 3).

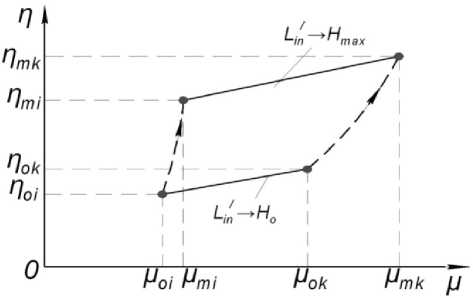
Рис. 4. Перемещение меток на фотоматрице при изменении уровня

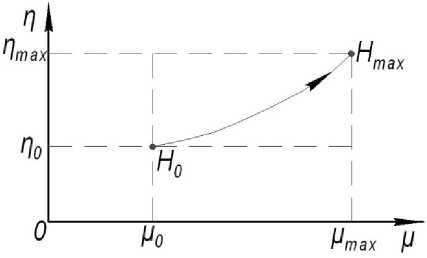
Рис. 3. Смещение координаты метки на фотоматрице в зависимости от уровня

Уровень и координаты меток связаны соотношениями (8). Тогда уровень можно найти из системы уравнений

xf _n = Yf

Z - H - f ^{, 11} Z - H - f mm

<

M n

Z m

X n f

-

H - f ’

П п

Y n f

Z m - H - f

L 2m = ( X n - X J² + ( Y n - Y )

При этом каждому значению уровня будет соответствовать точка на фотоматрице. Единственным условием применения метода является захват телекамерой метки на контролируемой поверхности при минимальном и максимальном значениях уровня, текущее значение которого определяется по формулам (9), (10). Очевидно, что измерения будут более точными, если мы сделаем отсчёт по отдельным координатам, но результат усредним

, (12) где H _M , H — уровень, определённый по формулам (9), (10) через соответствующие координаты. Контроль уровня по одной метке требует безусловного знания конструкционных параметров – фокусного расстояния f и высоты Z_m, что не всегда возможно.

2. Контроль уровня по двум меткам, расстояние между которыми известно. Это возможно, если метки создаются лазерными лучами, строго параллельным главной оптической оси телекамеры и ортогональными контролируемой поверхности. В этом случае также при смещении уровня вдоль оси Z координаты Х_i ,Y_i меток не изменяются, Z_i – Z_n = 0. В этом случае при изменении уровня будет изменяться расстояние между метками, (рис. 4).

где M^M n ; П —текущие координаты на изображении i -ой и n -ой меток соответственно. Из (13) получаем

M n ^- Mi

( X n - X ) f Z_m - H - f ’

X n - X 1 =

П п ^- n =

( Y n - Y i ) f _; Z m - H - f ’

( M n - M 1 )( Z m - H - f )

f

,

_Y - Y = ( П п - П 1 )( Z m - H - f ) n                            _f ^,

L n = ⁽ Z m ^- H " ^f ) V ( M n - M i )² + ( n n - П 1 )², (14)

Отсюда контролируемый уровень определяется из выражения

m

^^^^^B

f [1 +

,         Ln           ] = Z„

7( m „ ^- M i ^{)2 +} ( n „ ^- n ⁾²

- f (1 + L n ) , (15) L n

где L n = V ( M n - M i J² + ( n n - n i J² — расстояние между метками на фотоматрице.

Выражение (15) является функцией преобразования прибора, позволяющей определять уро-

вень по координатам метки.

3. Контроль по N меткам, расстояние между которыми известно. Метки создаются лазерными лучами, параллельным главной оптической оси телекамеры и ортогональными контролируемой поверхности. Для трёх меток i, k, n система (13) будет иметь вид

I         X. ff            Y ff a i = ———, n = ——

^{- 1} Z m - H - f '* Z m - H - f

X f        Yf

A ----i---, n - —i---- i Zm - H - f    Zm - H - f ц - Xi+i f   n -   Y+i f

‘+¹ Z m - H - f ^, ^n Z m - H - f

L ² , __v- ( X -1 - X i )² + ( Y -1 - Y )²

L ² , _+v - ( X i +1 - X i )² + ( Y +1 - Y .)²

, L² i -1, i +1 - ( X 1+1 - X i -1 )² + ( Y +1 - Y -1 )² .

Здесь значения L_{i-1, i} , L_{i , i+1} , L_{i-1 , i+1} – считаются известными. Координаты меток на изображении являются данными измерительной процедуры. Целью решения является определение уровня Н . Система (16) путём последовательных подстановок сводится к виду

L - 1 ,.- ^Z m ff ^ ( A - 1 - A ) 2 + ( n - 1 - n ) 2 “ L,, + 1 - ^ Z m - H^ f ) V ( A + 1 - a )² + ( n + 1 - n )² (17) ^L i - 1, i + 1 ^{- (} Z^m H ^f ) V ⁽ A + 1 ^- A ^{)2 + (} n + 1 ^- n ^{) 2}

Система (17) является вырожденной, так как размеры отрезков линейно связаны одним и тем же уравнением (9). По каждому из уравнений можно найти уровень H_i , но результат усреднить H - Z m - f [1 + ,       Li ^{+ 1}        ₂ ] - Z m - f (1 + L ^) .(18)

V ⁽ A +1 ^- A ) ^{+ (} n + 1 ^- n )                L i , i +1

H ^- N- ^ H,.          (19)

Усреднённый контроль уровня по нескольким меткам повышает точность измерений, в том числе компенсирует оптические искажения, если метки разбросаны по противоположным границам оптической системы.

Выражения (15)–(18) пригодны при горизонтальном положении контролируемого уровня, когда он ортогонален оптической оси. Реально оптическая ось может быть не ортогональна контролируемой поверхности, что имеет место быть при колебаниях резервуара, при этом уровень остаётся горизонтальным. Рассмотрим метод, позволяющий исключить влияние на результат измерений колебаний уровня относительно горизонта.

Выберем за ноль системы координат центральную точку объектива и оптическая ось объектива чтобы совпадала с осью Z . При выборе за начало координат других точек отсчета математическое описание процедуры формирования изображения сильно усложнится. Метки А_i на контролируемой поверхности формируются параллельными лазерными лучами, ортогональными к контролируемой поверхности (рис. 1). Расстояние между метками известно только при горизонтальной поверхности. При колебаниях уровня относительно оптической оси телекамеры оно изменяется. Из рис. 1 видно, что координаты X_i , Y_i меток А_i(X ; Y_i ; Z_i) не зависят от уровня Н . Если за начало координат принять центр оптической системы, то их можно считать известными, определяемыми конструкционными размерами прибора. От уровня зависят только координаты Z_i . Причём расстояние от каждой метки до поверхности будет разным и определяться через конструкционный параметр Z_m по формуле

Z i =Z m – H i , (20) где Н_i – уровень i -ойметки относительно горизонтального дна.

Возьмём четыре точки A,B,C,D, координаты X_A , Y_A , X_B , Y_B , X_C , Y_C , X_D, Y_D которых будем считать известными (рис. 5).

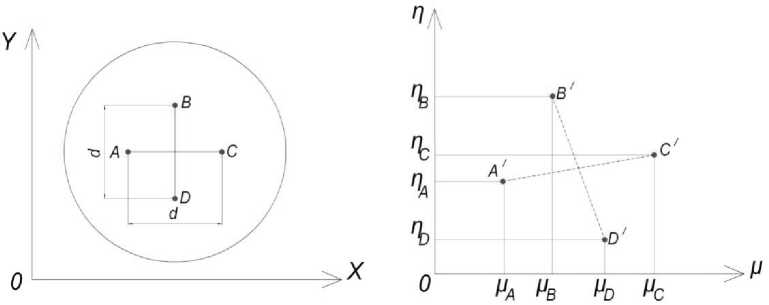
а)

б)

Рис. 5. Расположение лазерных меток: а – на контролируемой поверхности, б – на фотоприёмной матрице телевизионной камеры

Метки принадлежат одной плоскости, поэтому удовлетворяют уравнениям [5]

' P x ■ - a + P y ■ Y a + P z- Z a = 1 P x ■ - B + P y ■ Y B + P z" Z b = 1 ‘ P x ■ X c + P y ■ Y c + P z- Z c = 1 . P x ■ - d + P y ■ Y d + P z" Z d = 1 .

Здесь коэффициенты P_x, P_y, P_z , Z_A , Z_B , Z_C , Z_D , определяющие расположение плоскости в пространстве неизвестны. Однако известно [5], что при такой форме записи уравнения плоскости

P Z

Z _Ц

где Z_Ц – отрезок, отсекаемый плоскостью контролируемой поверхности по оси Z от начала координат, он и определяет расстояние от центра оптической системы до контролируемой поверхности и связан с искомым уровнем по формуле

H = Z_m – Z_ц . (23)

Учитывая, что оптические метки симметричны относительно начала координат, можно записать также но набрать нужное количество уравнений для определения неизвестных параметров, среди которых нас интересуют Z0, ZA , ZB , ZC , ZD , которые связаны с контролируемым уровнем по формуле (20), (23). Для контроля уровня по четырём точкам всего нам необходимо 9 уравнений. Исключив путём взаимных подстановок из уравнения (21) координату Z, получим систему из 4-х уравнений.

P ■ X_A + P ■ Ya + P ■ ^{( M a +} X A ) f = 1

xAyAz

M a

P x ■ X B + P y ■ Y B + P z ■ ^{( M} b ^{+ X} B ) ^f = 1

^M b            (26)

P ■ X_C + P ■ Y C + P ■ ^{( M c +} X C ) ^f = 1

Mc p .X +p .у +P ■(Md + XD)f = 1

• ¹    x ^л D ^{+ 1} y ^J D ^{+ 1} z                  ¹

Неизвестными и искомыми в этой системе являются P_x , P y , P_z , f .

Система нелинейная. Несмотря на то, система имеет четыре неизвестных, она не имеет решения, так как является вырожденной относительно фокусного расстояния. Для решения проблемы введём обозначение

Z ц = 4( Z a + Z b + Z c + Z d ) .   (24)

Обратимся к проекции меток на матрицу (рис. 5, б). Точки проекции будут иметь коорди-

на™ А ( ц A ; n A ) , B ( ц B ; n B ) , C ( Ц с ; П с ) -_u D ( h d ; П D ) • Учи тывая (5) для координат проекций каждой точки

-

f

Q = ^Pz^f = ^.       (27)

ZЦ

Тогда система (25) сводится к трём уравнениям

можно записать

M a =

XАf

z а - Г

П а =

YАf

P x ■ X a + P y ■ Y a + Q ■ (1 + - A ) = 1 M a

M b

Xf B

Zb — f ’

B

^M c Zc " f ’

^M d   Z d " f ’

Z а - f ,

П а =

Yf B

Z„ — f , B

Y C f

^П А   Z c "  f ’

П а =

YDf

Z D - ^f .

Оптическая система может состоять не из одной линзы, однако главное её назначение – пропорциональная передача изображения. Поэтому соотношения (24) универсальны и применимы для любых сколь угодно сложных оптических систем.

Параметры Ц A , П A , Ц B , n B , Ц C , П C , Ц D , П D являются данными измерительной процедуры, определяются по изображению и считаются известными.

Из совокупности соотношений (21) – (25) мож-

j P x ■ - B + P y ■ Y B + Q ■ (1 + - B ) = 1      (28)

M b

P x ■ - C + P y ■ Y c + Q ■ (1 + - C ) = 1 M c

Это линейная система, в которой нас интересует Q , имеет прямое решение по формулам Кра-

мера.

Q =

^Л Q

А

где

X A

Y A

+ - A

M a

А = -

X C

Y A

Y C

X B

M b

X

+ — C

M c

Y

, ^А Q

X B

X C

Y A

Y C

. (30)

Дальше при известном фокусном расстоянии из (26) получаем

f

Z Ц ^- Q.             (31)

Отметим, что при известном фокусном расстоянии величина Z0 может быть найдена из соотношения (24), которое с учётом (25),можно переписать в виде

X X X X

Z Ц - 0,25 f (4 +   + - ^ + - ^ + -D-) . (32)

μAμBμCμD

Искомый уровень нефтепродукта определяется по формуле (23).

Выражения (23), (29) – (32) определяют уровень колеблющейся относительно горизонта поверхности по координатам полученных на фотоматрице оптических меток и в совокупности определяют функцию преобразования прибора. Результаты, полученные по формулам (31),(32) можно усреднить. Выражение (31) предпочтительнее, так как оно не накладывает ограничений на симметричность лазерных меток относительно центра оптической системы и позволяет контролировать уровень по трём произвольным меткам, созданными на поверхности лазерными лучами, параллельными главной оптической оси.

Таким образом, общий алгоритм решения задачи определения уровня жидкости по четырём оптическим меткам в случаях горизонтальных колебаний уровня состоит в следующем:

• 1.    Для конкретных значений координат меток X_A,Y_A,X_B,Y_B, X_C,Y_C решаем систему уравнений (28), из которой находим параметр Q .

• 2.    По выражениям (31) – (32) находим искомый уровень.

• 3.    При необходимости результат усредняем

Описанные в статье оптические методы позволяют повысить точность измерения уровня жидкости, обеспечить контроль за наклоном резервуара, что дает возможность применять данные разработки на железнодорожном, автомобильном транспорте, а также на танкерном флоте.